利用卷积神经网络的太赫兹孔径编码增强成像 *

甘凤娇，罗成高，彭 龙，梁传英，王宏强

(1. 国防科技大学 电子科学学院， 湖南 长沙 410073； 2. 中国人民解放军78118部队， 四川 成都 610000)

高分辨雷达成像技术在军事和民用领域有迫切的应用需求，而太赫兹(0.1～10 THz)[1-2]雷达是实现高分辨成像的重要途径。相比于光学雷达成像，太赫兹波对云雾、烟尘、衣服等具有更强的穿透性，相比于微波雷达成像，太赫兹波波长短、带宽大，能实现更高分辨率的成像。传统的太赫兹雷达成像主要通过平台与目标之间的相对运动来实现方位、俯仰向的高分辨率，其系统结构复杂，成本高昂，难以实现前视凝视成像。因此基于太赫兹雷达成像和孔径编码成像的优势提出了太赫兹孔径编码成像技术。它主要是通过孔径编码来改变目标区域太赫兹波空间幅相分布来获取目标散射系数空间分布的一种成像方式，其在末制导、无损检测、安检成像等领域有一定的潜在应用价值。

2013年，美国杜克大学首次提出基于超材料孔径的计算成像方法，该方法利用频率扫描取代机械扫描，并在K波段实现了二维成像[3]。2016年，东南大学提出了基于可编程超表面微波段的成像方案，实现了对简单目标的成像[4-5]。2018年，浙江大学提出了基于随机场照明的微波成像系统，可以根据待成像目标尺寸和分辨率需求灵活设计系统参数，并搭建了实验系统进行了成像验证[6]。国防科技大学在太赫兹孔径编码成像技术方面开展了持续深入的研究，2017年率先在国内提出了太赫兹孔径编码成像方案[7]，随后对孔径编码的编码策略、高分辨近场三维成像以及孔径编码无相位成像等进行了研究并取得了一系列创新性研究成果[8-10]。

上述研究有力地推动了太赫兹孔径编码成像技术的发展，但其成像过程均依赖矩阵方程的计算求解，在太赫兹频段，由于分辨率较高，需要对成像目标进行精细化网格剖分，建立的矩阵成像方程规模庞大，这使得基于优化迭代思想的计算成像方法极为复杂，同时基于优化迭代的成像算法鲁棒性差，难以在低信噪比下实现高分辨成像。为此，本文考虑引入深度神经网络来解决这些问题。近年来，深度学习已成为各个领域的研究热点，在回归问题的求解上也获得了一系列的研究成果。2017年，美国麻省理工学院首次提出通过训练深度神经网络来解决计算成像中的求逆问题，并在无透镜成像中进行了验证实验[11]。随后美国加利福尼亚大学利用卷积神经网络从强度测量中恢复相位信息对全息图进行了重构，对孪生像和自干扰进行了抑制[12]。2019年，中国科学院也验证了深度神经网络在鬼成像中的优越性[13]。基于此，本文调查了基于卷积神经网络的太赫兹孔径编码成像算法在低信噪比下的成像性能。该算法利用卷积操作提取回波信号特征进行编码，然后在成像域进行解码，最终实现目标的反演。

1 系统结构设计和数学模型构建

1.1 基于单输入多输出技术的太赫兹孔径编码成像系统

针对安检与反恐等近距离成像的应用需求，基于透射式孔径编码天线设计了一种单发多收的太赫兹孔径编码成像(Terahertz Coded Aperture Imaging, TCAI)系统，如图1所示。该系统主要包括系统控制终端、矢量网络分析仪、发射机、编码模块、孔径编码天线、接收阵列。

图1 太赫兹孔径编码成像系统Fig.1 TCAI system

系统控制终端同时控制矢量网络分析仪和编码模块，其中矢量网络分析仪通过外接发射机和接收阵列来收发太赫兹信号，孔径编码天线在编码模块的驱使下对入射太赫兹波信号的相位或者振幅进行随机调制，获得时空独立的随机辐射场。然后经过目标反射的伪随机信号被接收阵列接收。与此同时，系统控制终端结合发射信号和成像系统结构参数，进行辐射场信号推演，得到参考信号矩阵。最终将参考信号矩阵和回波信号送入系统控制终端利用计算成像思想实现目标的反演。其中，成像平面从方位维和俯仰维被剖分为M个成像网格。

1.2 成像数学模型构建

假设太赫兹孔径编码成像系统发射线性调频信号，其形式可表示为：

(1)

式中，St(t)是发射单元在t时刻的发射信号，fc是中心频率，A是信号幅度，j为虚数单位，K是调频率。

发射的太赫兹波信号首先照射到孔径编码天线的表面，如果孔径编码包含Q个编码阵元，那么到达第q个编码阵元的太赫兹波信号为：

(2)

式中，dTx,q表示第q个编码阵元与发射天线之间的距离。经过编码天线调整后，第m(m=1,2,…,M)个网格单元处tn时刻的辐射场信号为：

(3)

式中，dq,m为第q个编码单元到成像平面第m个网格单元的距离，Aq(tn)和φq(tn)是第q个编码单元在tn时刻的幅度调制因子和相位调制因子。对于幅度调制编码天线，φq(tn)≡1；对于相位调制编码天线，Aq(tn)≡1。

经过目标散射后，tn时刻到达第h个接收天线的回波信号可写为：

(4)

式中：βm是成像平面中第m个网格的散射系数；Sh(tn)是第h个接收天线对应的参考信号矩阵，结合方程(3)可写为式(5)形式。

(5)

式中，dm,h是第m个网格到第h个接收天线的距离。

综上，在tn时刻基于单输入多输出技术的太赫兹孔径编码成像系统的数学模型可写为：

Sr(tn)=S(tn)·β

(6)

(7)

由于成像系统进行了N次孔径编码和时间采样，基于单输入多输出技术的太赫兹孔径编码成像系统的数学模型可写为：

Sr=S·β+ω

(8)

式中：Sr为基于单输入多输出技术的太赫兹孔径编码成像系统对应的回波信号矢量，Sr=[Sr(t1),Sr(t2),…,Sr(tN)]T；S为基于单输入多输出技术的太赫兹孔径编码成像系统对应的参考信号矩阵，S=[S(t1)，S(t2)，…，S(tN)]T；ω为添加到回波信号中的白高斯测量噪声，ω=[ω1,ω2,…,ωN·H]T。

从成像模型的推导过程中可以看出，方程(8)的求解主要依赖参考信号矩阵S的推导以及它的行与行、列与列之间的非相关性。编码天线调制能力越强，S的非相关性越强，目标散射系数的求解就越精确。

2 目标散射系数的求解方法和成像网络的设计和训练

2.1 目标散射系数的求解方法

在之前的太赫兹孔径编码成像中，目标散射系数求解问题被看成一个优化问题。其通常需要一定的先验信息和大量的优化迭代来重建目标。然而基于卷积神经网络的太赫兹孔径编码成像方法利用生成的训练数据训练成像网络，然后利用网络从回波信号中精确反演目标。两种方法的处理框架如图2所示。虚线表示经典成像算法的求解框架，其中参考信号矩阵通过辐射场推演得到；实线表示提出的成像算法的处理框架。在这里离线成像网络被看成一种强大的映射操作，而这种映射操作可以通过大量蕴含系统配置和参数的输入输出例子学习得到，其数学表达式可以写为：

findβ

s.t.β=G(Sr)

(9)

其中，G是需要训练的离线网络。

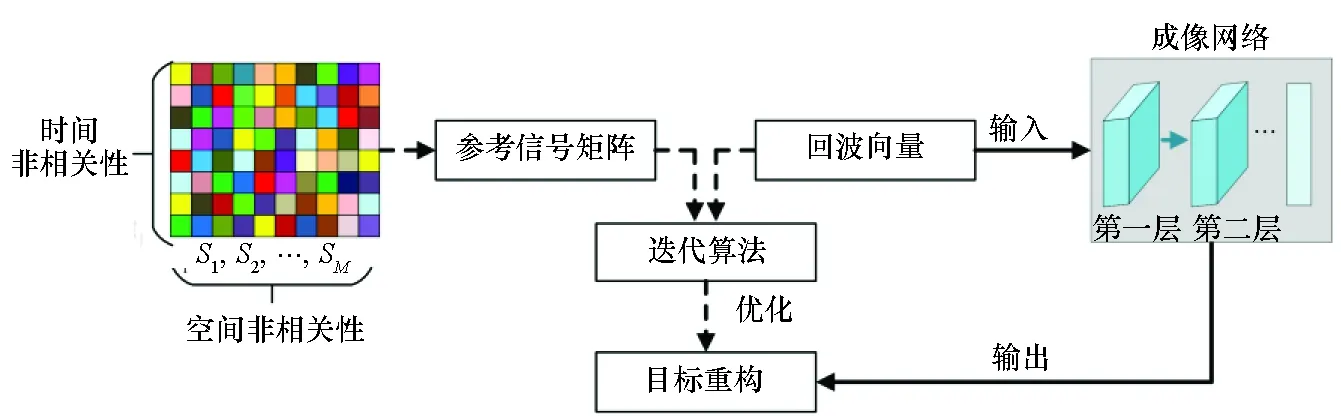
图2 太赫兹孔径编码成像处理框架的比较Fig.2 Comparison of processing frameworks for TCAI

根据式(7)可以看出，参考信号矩阵的规模庞大，然而在太赫兹频段，由于分辨率较高，需要对成像目标进行精细化网格剖分，建立的矩阵成像方程规模将更庞大，这使得基于优化迭代思想的成像算法计算极为复杂，同时参考信号矩阵难以精确估计。因此提出利用大量的输入输出示例来训练网络，从而修复建模误差和增强算法的鲁棒性，最终实现低信噪比下的高分辨成像。

2.2 成像网络的设计和训练

卷积神经网络是一种局部连接、权重共享的前馈神经网络，它的人工神经元可以响应一部分覆盖范围内的周围单元，对于图像处理有出色表现。因此考虑利用卷积神经网络来实现回波信号到目标图像的映射。成像网络结构的设计如图3所示，其包含了提取回波信号浅层特征和高层特征的卷积层和下采样层，避免梯度消失的批标准化处理层，增加网络表达能力的激活层，其中的激活函数是修正线性函数ReLU(x)=max{0,x}，完成特征融合的上采样和连接操作，以及实现特征域到成像域转换的传输层。

图3 太赫兹孔径编码成像网络结构示意图Fig.3 Schematic diagram of network structure for TCAI

深度网络具有强大的求逆能力，但这种能力是由其包含的大量自由参数和灵活的网络结构提供的。因此网络设计好后，网络的训练和模型参数的优化是两个极其重要问题。

对于成像网络的训练，其实际就是最小化损失函数，让预测目标一直不断地逼近真实目标的过程。其主要包括计算残差的前向传播过程和通过优化参数使得残差最小化的后向传播过程。在前向传播过程中，信号从输入层向输出层单向传播，然后通过损失函数计算残差。在后向传播过程中，将残差从输出层向隐藏层反向传播，直至传播到输入层。通过求得的残差对成像模型的参数进行更新，最终通过不断迭代获得一个稳定的成像模型。下面以全连接神经网络为例简单地描述太赫兹孔径编码成像的前向传播和后向传播过程，如图4所示。

根据图4中的描述，网络的前向传播过程可以表示为：

Zl=Wlσ(Zl-1)

(10)

式中，Zl表示第l层(l=1,2,…,L)经过激活函数之前的输出，Wl表示第l层的权重矩阵，σ表示激活函数。在训练过程中，针对要解决的问题选取均方误差损失函数来度量神经网络的预测目标β*和真实目标β之间的差异，其表达式如式(11)所示。

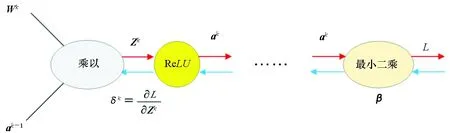
图4 太赫兹孔径编码成像网络的前向传播和后向传播示意图Fig.4 Schematic representation of forward and backward propagation of TCAI network

(11)

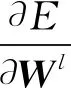
=[(Wl+1)Tδl+1⊙σ′(Zl)](aL-1)T

=δl(aL-1)T

(12)

式中，⊙是阿达马积，δl=∂E/∂Zl表示第l层误差，δl+1表示l+1层误差，σ′表示激活函数的导数。

对于网络参数的更新，采用自适应矩估计的方法，即Adam算法[14]。该方法能基于训练数据迭代地更新神经网络权重。它和经典的随机梯度下降不同, 经典的随机梯度下降方法保持单一的学习率更新所有权重，而Adam算法通过计算梯度的一阶矩估计和二阶矩估计为不同的参数设计独立的自适应性学习率。假设在第l层的第e-1批数据时更新的参数为We，那么在第l层的e批数据参数更新可以表示为：

(13)

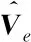
(14)

(15)

式中：β1和β2分别是一阶矩估计的指数衰减率和二阶矩估计的指数衰减率；ε是一个平滑项，其作用是防止分母为零；∂E/∂We-1表示的是损失函数在l层的e-1批数据中所有数据对权重梯度的均值。

从式(3)中可以看出，Adam算法在更新参数的时候考虑了所有的历史情况对现在参数更新的影响，既保证了下降梯度方向的正确性，又为每一个参数设置合适的下降步长，使得网络快速平稳地收敛到合适的状态。

综上，网络的整个训练过程是先对神经网络各层参数即各层的权重矩阵和偏置项进行初始化，设置好训练的最大迭代次数、每个训练批的大小和学习率。再从训练数据中取出一批数据，从该批中取出一个数据，包括输入回波信息以及对应的真实目标。然后将回波信号送入输入端得到各层的输出参数。再根据网络的预测目标和真实目标计算网络的损失函数以及计算损失函数对输出层的误差，利用相邻层之间的误差递推公式计算每一层的误差，利用每一层的误差求出损失函数对每一层参数的导数。接着循环完所有的批数据并将它们求和，利用Adam算法更新各层的参数。最后迭代循环使网络收敛至合适的解。整个训练过程的如图5所示。

图5 太赫兹孔径编码成像网络结构训练流程图Fig.5 Flowchart of network structure training for TCAI

3 仿真实验结果

基于卷积神经网络的太赫兹孔径编码成像系统参数见表1。发射的太赫兹信号的中心频率为340 GHz，孔径编码天线采用了离散相位调制，因此Ap(tn)≡1。根据文献[15]中的研究, 目标的稀疏度可以用L1范数和L2范数来表征。

(16)

显然稀疏度的取值在0和1之间；当且仅当β只包含一个非零分量时，稀疏度为1；当且仅当所有分量相等时，稀疏度为0。训练数据的生成主要利用式(8)通过仿真来得到，其中一部分数据用于验证网络，一部分数据用于训练网络，二者的比例为1 ∶10。最终网络的训练在一台GPU NVIDIA 2080的台式电脑上完成。成像算法的代码利用了MATLAB和Tensorflow。

表1 太赫兹孔径编码成像系统参数

为了验证系统高分辨特性和设计的合理性，分析了参考信号矩阵S。随机辐射场分布、空间非相关性以及时间非相关性分布如图6所示。从结果中可以看出辐射场分布的非相关性强，随机性强，其非常有利于高分辨太赫兹孔径编码成像。

(a) 随机辐射场分布(a) Distribution of random radiation fields

(b) 空间相关函数(b) Spatially correlated functions

(c) 时间相关函数(c) Time correlated functions图6 参考信号矩阵的分布特性Fig.6 Distribution characteristics of the reference signal matrix

为了验证本文方法的成像性能，在不同信噪比下对不同稀疏度目标进行了仿真实验，其中目标的稀疏度分别为0.958 6，0.777 2，0.463 0，0.656 3。成像结果如图7所示，从图中可以看出：成像网络能够较好地重建各种目标，其成像性能与目标的稀疏度有关，其关系是随着稀疏度的减小目标成像结果变差。对于不同信噪比下的目标成像，可以看出随着信噪比的增加网络的成像性能不断增加。值得一提的是，网络能够在SNR=-5 dB的信噪比下对扩展目标成像，虽然成像结果失真且存在伪散射点，但是基本的语义信息都得到了正确的恢复。

为了进一步验证本文方法的优越性，在SNR=5 dB的条件下考察了不同成像方法对不同稀疏度目标的重建，成像结果如图8所示。其中，原始目标的稀疏度分别为0.870 4，0.796 5，0.712 1，0.645 8。从实验结果中可以看出，不论对于稀疏目标还是扩展目标，本文方法在低信噪比下相比经典的正交匹配追踪(Orthogonal Matching Pursuit, OMP)算法[16]、全变分增广拉格朗日交替方向算法(Total Variation Augmented Lagrangian Alternating Direction Algorithm, TVAL3)[17]和稀疏贝叶斯学习(Sparse Bayesian Learning, SBL)成像算法[18]能够得到更高分辨率的重构目标。

图7 不同稀疏度目标在不同信噪比下的成像结果Fig.7 Imaging results for different sparse targets at different SNRs

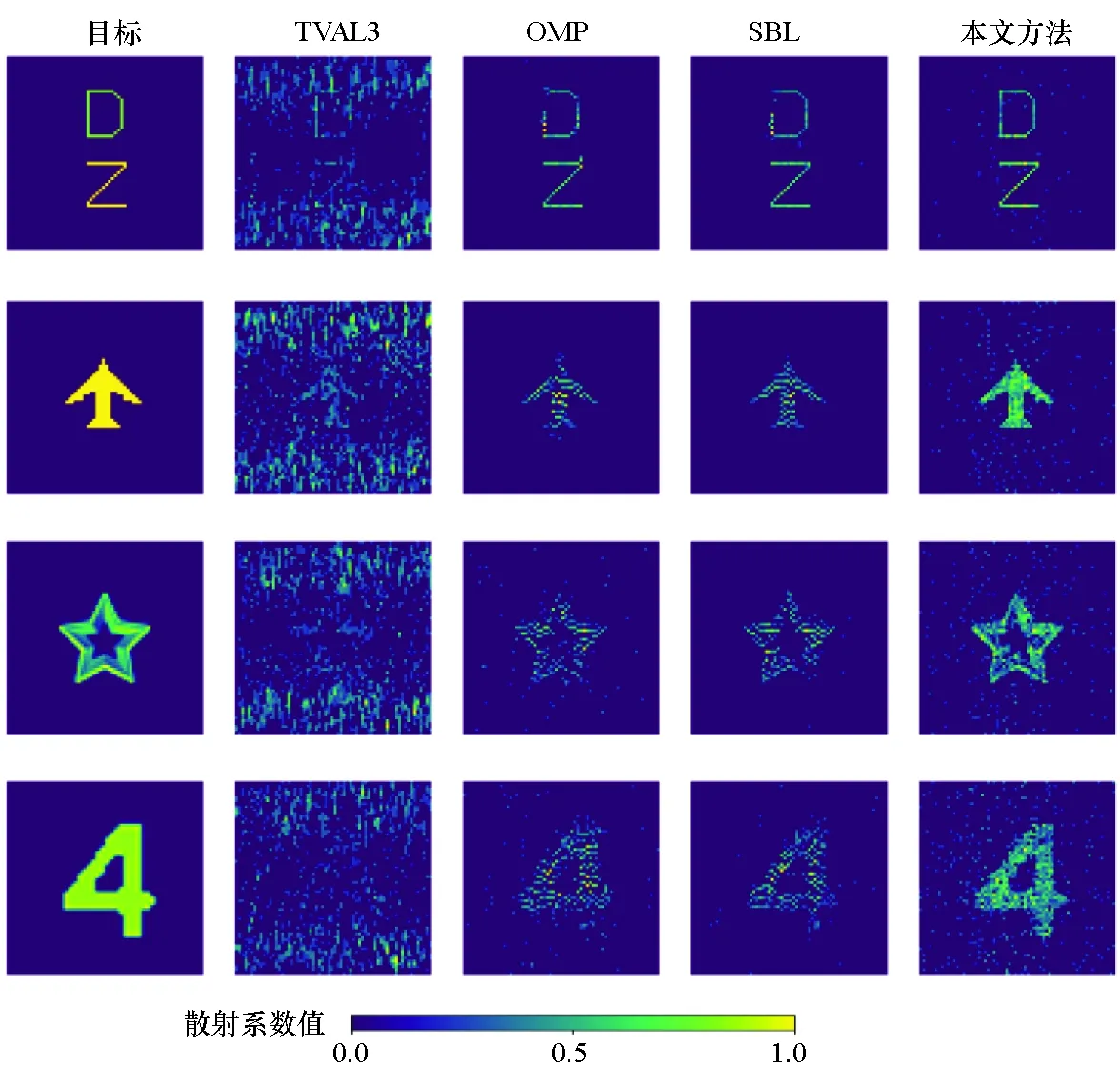
图8 SNR=5 dB时不同成像算法的性能比较Fig.8 Comparison of the performance of different imaging algorithms at SNR=5 dB

4 讨论

上述实验证明了基于卷积神经网络的太赫兹孔径编码成像算法在低信噪比下具有良好的成像性能。接下来讨论成像网络的泛化性能，进一步的仿真实验在混合国家标准与技术研究所数据集[19](Mixed National Institute of Standards and Technology database, MNIST)上进行，结果如图9所示。

图9 成像网络在SNR=5 dB时在MNIST的重建结果Fig.9 Reconstruction results of the imaging network on MNIST when SNR=5 dB

可以看出，本文成像网络在MNIST测试集上具有良好的重建性能，虽然重建目标存在许多伪散射点，但重建目标的语义信息与原始目标高度一致。另外，为了进一步评价成像网络的泛化性能，从MNIST中随机选取了50个不同稀疏度的目标进行了50次蒙特卡洛实验，并计算了其皮尔逊相关系数。在SNR=5 dB时，其50次的皮尔逊相关系数均值为0.764 7，由此可知本文成像网络具有良好的泛化性能。

5 结论

本文提出基于卷积神经网络的太赫兹孔径编码增强成像方法，该方法实现了对成像系统隐式建模，不依赖复杂的先验知识，显著降低了成像计算复杂度，在低信噪比下提高了成像分辨率。首先建立了太赫兹孔径编码成像系统数学模型，分析了成像处理框架，然后设计了卷积神经网络结构并介绍了网络的训练方法，最后给出了仿真实验结果。实验结果表明，本文方法相比经典的成像算法在低信噪比下对不同稀疏度目标的重构有一定优势。本文方法在末制导、无损检测、安检等领域具有一定的潜在应用价值。