地球静止轨道卫星系统兼容性多维度分析方法 *
2022-01-26董苏惠姚秀娟
董苏惠,高 翔,韩 锐,姚秀娟,闫 毅
(1. 中国科学院国家空间科学中心 复杂航天系统电子信息技术重点实验室, 北京 100190;2. 中国科学院大学, 北京 100049; 3. 国家无线电监测中心, 北京 100037)
近年来,随着卫星成功发射数量的迅猛增加,卫星频率和轨道资源愈加紧张,尤其是地球静止轨道(Geostationary Satellite Orbit, GSO)卫星的资源竞争异常激烈[1],在全球360°地球静止轨道上,平均不到1°就有1颗卫星,而世界各国必须按照国际电信联盟(International Telecommunication Union, ITU)的《组织法》及《无线电规则》等,在划分的空间业务频段内,遵循“先登先占”原则[2]。因此,越优先掌握频谱资源,在频率使用和协调过程中将占据越有利地位,考虑到多个协调对象已有在轨卫星,全球的频率协调难度大大提升。为了支撑国内外频率协调工作的顺利实施,研究频轨资源相关的标准体系和协调方法具有重要意义。国内外在该方面已经开展了很多工作[3-6],本文在此基础上,梳理了卫星网络协调的保护标准及ITU相关建议书[7-12],在GSO 卫星固定业务之间的干扰分析中,建议书ITU-R S.738、S.737、S.739主要采用等效噪声温度增量百分比ΔT/T的干扰分析方法,提出在上行和下行链路中,ΔT/T的值应该与6%的门限值进行比较[7-9]。建议书ITU-R S.740、S.741采用载波干扰比(Carrier-to-Interference Ratio, CIR)的干扰分析方法,CIR值由载波噪声比(Carrier-to-Noise Ratio,CNR)和调整因子得出,即C/I=C/N+k,k一般为12.2 dB或14 dB,具体可参考ITU-R S.741建议书提出的单入干扰(Single Entry Interference, SEI)的保护标准[10-11]。建议书ITU-R S.1432-1将系统噪声的百分数转换成相应的干扰噪声比(Interference-to-Noise Ratio,INR)来表示干扰容限,提出I/N=-12.2 dB的干扰门限值,其他卫星业务和场景也可参考该值[12]。
现有文献[3,13-16]在GSO卫星系统兼容性分析的研究中,大多围绕固定卫星轨位间隔的场景来开展,暂未发现在GSO卫星轨道位置、系统链路可用度以及干扰地球站选址等维度上进行精细化颗粒度的分析,大多在单一维度上进行干扰评估,且干扰分析的结果在某一确定维度上的变化特征没有得到直观体现,也并未区分不同维度对分析结果的影响程度,现有公开资料未查阅到与现有专业软件Visualyse分析结果的比对论证。
本文构建了单波束及多波束GSO卫星系统的干扰场景,在干扰分析时考虑了GSO卫星轨道、系统链路的可用度及干扰系统地球站选址等维度,在不同维度间进行横向对比,细化各维度干扰评估时的颗粒度,突破了传统单一维度和粗颗粒度干扰评估方法的局限性,在进行综合干扰分析时可以反映出各个维度的特征,如对干扰分析结果的影响方向、程度和增量的变化情况。本文还提出了不同轨位间隔下干扰系统地球站选址的建议,为GSO卫星系统间的干扰规避提供参考。基于多维度的GSO卫星系统兼容性分析方法还结合了链路损耗中的多种影响因素(如降雨、云或雾、大气引起的衰减等),对于GSO卫星系统干扰评估效能的提升具有一定的借鉴意义。
1 频率覆盖问题的研究
本节主要研究GSO卫星系统间的同道干扰,设受扰卫星系统的通信链路载波频率为f,通信链路带宽为W;干扰卫星系统的通信链路载波频率为fi,通信链路带宽为Wi。则两个系统间的重叠频带宽度WOverlap如式(1)所示。
(1)
(2)
其中,
(3)
以Ka上行频段(27.5 ~ 31 GHz)为例,图1反映了国内部分GSO卫星系统在该频段范围内的频段占用情况,图1数据来源于ITU公开资料。由图1可见,众多GSO卫星系统的多频段同频共用问题十分普遍,本文主要研究带内干扰情况。

图1 国内部分GSO卫星系统在27.5~31 GHz内的频段占用情况Fig.1 Occupation of some domestic GSO satellite systems in the 27.5~31 GHz
2 基于系统链路可用度的研究
卫星系统的可用度常用系统链路可用度来近似代替,假定一年p%的时间中,卫星系统链路中断,则链路可用度为一年中系统链路的误比特率(Bit Error Rate, BER)不超过给定的门限值的概率P,即
P=1-p%
(4)
卫星系统链路可用度主要受电波传播模型及硬件故障等因素影响,忽略硬件故障等较小的影响因素,本节重点研究电波传播模型对不同通信链路的影响。其中,雨衰主要对5 GHz以上的电磁波有影响,大气衰减和云雾衰减主要对10 GHz以上的电磁波有影响[17-23],由此可见在对K、Ka频段的卫星进行干扰分析时降雨以及云雾的影响不可忽视。
GSO卫星选取CHNSAT-81.5E卫星,分别研究该卫星与喀什(39.5°N,75.9°E,1 307 m)、密云(40.4°N, 116.8°E,109 m)、三亚(18.3°N,109.3°E,22 m)三个地球站间星地链路的降雨引起的传播损耗随通信频率的变化特性曲线,如图2所示;云雾引起的传播损耗随通信频率的变化特性曲线,如图3所示;大气引起的传播损耗随通信频率的变化特性曲线,如图4所示;其中,图2~4中的数据来源于ITU公开的资料[17-23],GSO-三站星地链路的地球站仰角依次是44.24°、 31.21°、 51.88°,极化方式为混合极化,超过降雨的衰减时间百分比为0.01%,超过云雾衰减的时间百分比为0.1%。
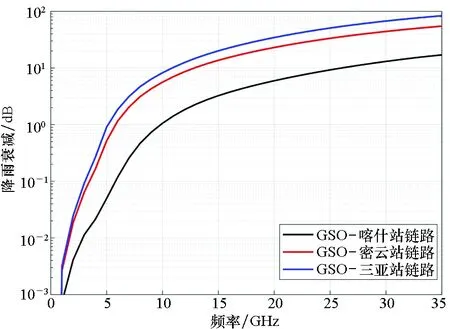
图2 星地链路中降雨引起的传播损耗随通信频率的变化特性曲线Fig.2 Variation characteristics curves of propagation losscaused by rainfall with communication frequency in the satellite-earth link
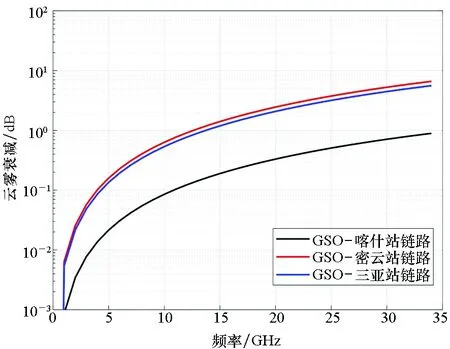
图3 星地链路中云雾引起的传播损耗随通信频率的变化特性曲线Fig.3 Variation characteristics curves of propagation loss caused by cloud and fog with communication frequency in the satellite-earth link

图4 星地链路中大气引起的传播损耗随通信频率的变化特性曲线Fig.4 Variation characteristics curves of propagation loss caused by atmosphere with communication frequency in the satellite-earth link
K、Ka频段卫星-三站的自由空间损耗值相近[24],由图2~4可知,三站中喀什站电波传播模型引起的衰减值最小,考虑到电波传播模型是影响该频段星地链路传播损耗的主要因素,因此三站中CHNSAT-81.5E卫星-喀什站的星地链路的传播损耗最小。在下节的GSO系统间的干扰分析中,可以选择喀什站作为待分析的地球站,将得到比其他两站更大的链路干扰。
由图2~4可知,在降雨、云雾、大气等因素中,降雨是影响卫星通信链路的关键因素,在研究GSO卫星系统链路可用度对干扰分析结果的影响时,需重点研究链路雨衰与系统链路可用度的关系。
分别研究通信频率为30 GHz及20 GHz时,CHNSAT-81.5E卫星至喀什、密云、三亚三站的降雨引起的衰减与系统链路可用度的变化特性曲线,如图5所示。
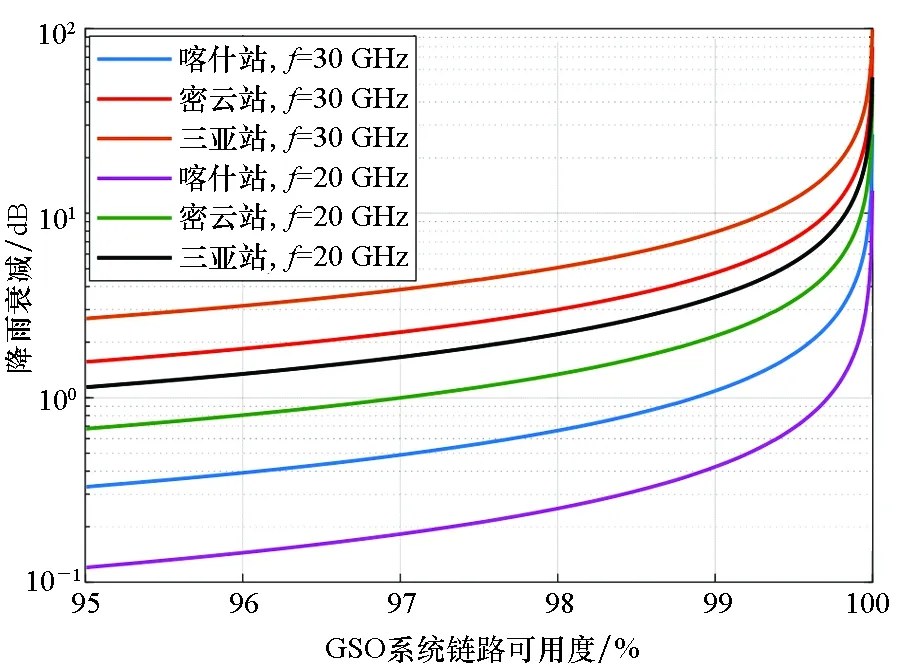
图5 CHNSAT-81.5E卫星至喀什、密云、三亚三站的降雨引起的衰减随系统链路可用度的变化特性曲线Fig.5 Variation characteristics curves of CHNSAT-81.5E satellite to Kashi, Miyun, Sanya three stations rainfall attenuation with the system link availability
由图5可知,对于同一通信链路而言,GSO系统链路的可用度越高,则超过降雨衰减的时间百分比越低,GSO系统链路的可用度越高,雨衰对通信链路的影响越大,且当GSO系统链路可用度超过99.99%时,雨衰的影响急剧增大。
3 单波束GSO卫星系统间的研究
3.1 基于GSO卫星轨位间隔研究

图6 单波束GSO卫星系统间的干扰场景Fig.6 Interference scenarios between single-beam GSO satellite systems
图6为单波束GSO卫星系统间的干扰场景,主要针对单条恒联通链路对单条恒联通链路的干扰影响研究,在该干扰场景下,受扰GSO卫星系统接收机的数学干扰模型可以用干扰噪声比I/N来表示[25],其中,下行I/N如式(5)所示,上行I/N如式(6)所示。
(5)
式中:I为受扰系统接收到的干扰信号功率,W;N为受扰系统接收机的等效噪声功率,W;p′s为干扰卫星的发射功率,W;g′1(θ1)为干扰卫星天线的发射增益,θ1为干扰卫星发射天线的离轴角,(°);g2(θ2)为受扰地球站天线的接收增益,θ2为受扰地球站接收天线的离轴角,(°);Te为受扰地球站下行接收端的等效噪声温度,K;Wd为受扰系统下行通信链路的带宽,Hz;k=1.38×10-23J/K为玻尔兹曼常数。
(6)
式中:p′e为干扰地球站的发射功率,W;g′3(θ3)为干扰地球站天线的发射增益,θ3为干扰地球站发射天线的离轴角,(°);g4(θ4)为受扰卫星天线的接收增益,θ4为受扰卫星接收天线的离轴角,(°);Ts为受扰卫星上行接收端的等效噪声温度,K;Wu为受扰系统上行通信链路的带宽,Hz。
lsi→e和lei→s分别为下行及上行干扰通信链路的传输损耗,其包含:自由空间损耗Ls,馈线损耗Lf,天线指向误差损耗Lap,极化损耗Lp,降雨引起的衰减Lr,云或雾引起的衰减Lc,大气吸收引起的衰减La[17-24]。
选取CHNSAT-81.5地球同步轨道卫星作为受扰系统GSO卫星,选取的受扰及干扰地球站位于喀什的同一位置,考虑GSO系统链路可用度的影响,分析干扰GSO卫星系统在不同轨位间隔下两个系统间的干扰噪声比的变化特性,其中受扰及干扰GSO卫星系统干扰场景所使用的波束及空口参数参考频率信息通报(International Frequency Information Circular, IFIC),下行链路如表1所示,上行链路如表2所示。
表1~2中,地球站天线方向图参考ITU公布的建议书ITU-R S.580-6[26]或ITU-R S.465-6[27],星上天线方向图参考建议书ITU-R S.672-4[28]。
图7、图8分别反映了干扰系统GSO卫星在不同轨位以及系统链路可用度条件下的下行和上行链路I/N的变化特性,坐标轴分别代表干扰系统GSO卫星与受扰系统CHNSAT-81.5地球同步轨道卫星的轨位间隔、GSO系统链路的可用度。
由图7和图8可知,当GSO系统链路可用度为99.99%时,对于下行链路,轨位间隔为2°时的I/N为-13.77 dB,轨位间隔为0.1°时的I/N为9.08 dB;对于上行链路,轨位间隔为2°时的I/N为-27.95 dB,轨位间隔为0.1°时的I/N为-3.51 dB。
在系统链路可用度一定的条件下,两个卫星系统的轨位间隔>2°时,I/N变化缓慢;轨位间隔≤2°时,I/N变化较快,尤其是轨位间隔≤0.1°时,出现I/N急剧上升现象。在卫星系统间的轨位间隔一定的条件下,系统间的I/N随着系统链路可用度的增大而减小,且变化幅度远小于轨位间隔引起的I/N变化幅度。

表1 卫星系统下行链路干扰场景波束及空口参数

表2 卫星系统上行链路干扰场景波束及空口参数

图7 干扰系统GSO卫星在不同轨位以及系统链路可用度条件下的下行链路I/N变化特性曲面图Fig.7 Downlink I/N variation surface map of interference system GSO satellite in different orbits and system link availability

图8 干扰系统GSO卫星在不同轨位以及系统链路可用度条件下的上行链路I/N变化特性曲面图Fig.8 Uplink I/N variation surface map of interference system GSO satellite in different orbits and system link availability
3.2 基于干扰系统地球站选址研究
参考表1中的下行链路波束及空口参数,选取CHNSAT-81.5地球同步轨道卫星、喀什地球站组成受扰系统,GSO系统链路可用度为99.9%,分析干扰卫星与受扰系统卫星在不同轨位间隔、干扰系统的地球站与受扰地球站在不同距离差值下I/N的变化特性,如图9所示。
分析不同轨位间隔下干扰系统地球站最近选址距离,可以为GSO卫星系统的干扰规避提供参考。由图9可知,当干扰卫星与受扰系统卫星轨位相差0.1°时,干扰系统地球站距受扰地球站1 325 km左右时下行链路I/N满足ITU的-12.2 dB限值条件;轨位间隔相差0.5°时,干扰系统地球站距受扰地球站279 km左右时下行链路I/N满足限值条件;当干扰系统地球站在距受扰系统地球站321~788 km选址时,下行链路I/N的值基本保持不变。

(a) 干扰系统在不同轨道和地球站位置条件下的下行链路I/N变化特性曲面图(a) Downlink I/N variation surface map of interferencesystem in different orbits and earth station locations

(b) 下行链路I/N随干扰系统地球站选址的变化特性曲线(b) Variation characteristics curves of downlink I/N with interference system earth station locations图9 干扰系统在不同轨道和地球站位置条件下的下行链路I/N分析Fig.9 Downlink I/N analysis of interference system in different orbits and earth station locations
4 多波束GSO卫星系统间的研究
多波束GSO卫星系统间的集总干扰场景,如图10所示,干扰系统B的点波束数量为m,受扰系统A的点波束数量为n。

图10 多波束GSO卫星系统间的集总干扰场景Fig.10 Integrated interference scenario between multi-beam GSO satellite systems
选取CHNSAT-81.5作为受扰系统GSO卫星,干扰系统GSO卫星位于与受扰系统GSO卫星间隔[-6°,6°]的轨位区间内,下行链路使用的波束及空口参数参考表1,上行链路参数参考表2,受扰及干扰系统的波束数量n、m均为10,卫星波束间采用四色划分频分多址(Frequency Division Multiple Access, FDMA)的多址方式。考虑到波束间业务需求的不均匀性,假设干扰系统中的第i个波束的业务需求量为80+10(i-1) Mbit/s,按照波束业务需求量公平性地对干扰及受扰系统进行功率分配[29]。图11和图12反映了干扰系统GSO卫星在不同轨位间隔以及系统链路可用度条件下的下行及上行链路集总I/N的变化特性。

图11 多波束GSO系统在不同轨位间隔以及系统链路可用度条件下的下行链路集总I/N变化特性曲面图Fig.11 Downlink integrated I/N variation surface map of multi-beam GSO systems in different orbits and system link availability

图12 多波束GSO系统在不同轨位间隔以及系统链路可用度条件下的上行链路集总I/N变化特性曲面图Fig.12 Uplink integrated I/N variation surface map of multi-beam GSO systems in different orbits and system link availability
由图11和图12可知,对于多波束卫星系统,同样地,在系统链路可用度一定的条件下,两个卫星系统的轨位间隔>2°时,I/N变化缓慢;轨位间隔≤2°时,I/N变化较快,尤其是轨位间隔≤0.1°时,出现I/N陡升现象。并且系统间的I/N随着系统链路可用度的增大而减小。
5 案例对比分析
Visualyse软件由英国TSL公司开发,基于ITU的标准和规则,用于开展国际间频率轨道协调,对高低轨卫星的干扰分析计算已被ITU高度认可和采纳。本节使用的方法同样依据ITU的相关建议书和规则,在分析时增加了多维度的影响因素,并细化了每个维度的分析颗粒度,使干扰分析结果的表征直观形象。
依据第2、第3节的研究,在此基础上分析现有GSO卫星系统间的选频、选轨方法,并将分析得到的干扰结果与Visualyse软件结果进行比对和验证。
本节仍以CHNSAT-81.5卫星作为受扰系统卫星,选取的受扰及干扰地球站位于喀什的同一位置,选取与CHNSAT-81.5卫星轨位间隔1°的INSAT-KA82.5E卫星作为干扰系统的GSO卫星,其中CHNSAT-81.5卫星系统的波束及空口参数参考频率信息通报,本节计算的波束间干扰结果见表3。

表3 分析结果与Visualyse结果比对(暂不考虑电波传播模型的影响)Tab.3 Comparison of analysis results with Visualyse results (excluding the electromagnetic wave propagation loss)
在保证GSO系统链路可用度高达99.99%的条件下,选取表3的第1、第3、第9三组场景,并考虑电波传播模型对干扰结果的影响,本文的计算结果与Visualyse的结果对比见表4,表4中GSO系统链路可用度达99.99%。
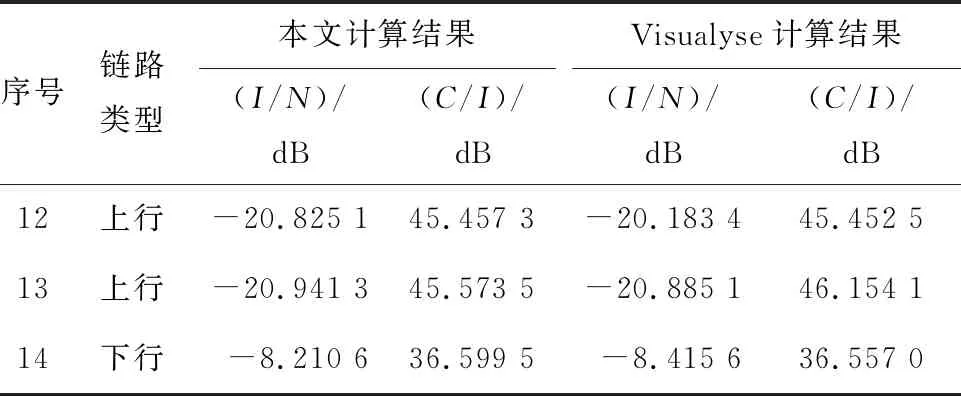
表4 分析结果与Visualyse结果比对(考虑电波传播模型的影响)
本文计算波束间的干扰结果与Visualyse结果间的误差如图13所示。

图13 计算结果与Visualyse结果的误差分析Fig.13 Error analysis of calculation and Visualyse results
由图13的对比分析可以得出,本文I/N及C/I的计算结果与Visualyse的误差基本保持在0.7 dB范围以内,验证了本文干扰评估方法的有效性。
6 结论
针对GSO卫星系统间的同道干扰问题,结合ITU提供的电波传播模型、天线波束等参数,分别建立了单波束及多波束GSO卫星系统干扰分析的数学模型。
1) 在GSO卫星轨道位置、系统链路可用度以及干扰地球站选址等维度上进行精细化颗粒度的分析,避免了传统单一维度和粗颗粒度干扰评估方法的局限性,不同维度间进行横向对比, 分析了GSO卫星系统在不同维度下的干扰变化特性曲线,并比较了各维度对干扰分析结果的影响程度。
2) 在满足ITU干扰限值条件下,提供了下行干扰场景中不同GSO卫星轨位间隔下的干扰系统地球站最近选址的方法,可以为GSO卫星系统的干扰规避提供参考。
3) 本文I/N和C/I计算结果与Visualyse软件计算结果的误差基本保持在0.3%,证明了本文方法的有效性,对支撑GSO卫星系统的国内外资源协调、干扰分析具有一定的借鉴意义。
