岸舰导弹作战单元多目标投送模型及解算方法

姜子劼，宋贵宝，刘 战，刘镇毓

（海军航空大学，山东 烟台 264001）

0 引言

20 世纪中叶以来，随着导弹总体技术和精确制导技术的不断发展，各型岸舰导弹逐渐成为陆上对海作战中的重要力量［1］，而机动式岸舰导弹具备机动性、灵活性和隐蔽性等突出优势，能够适应各种兵力机动能力迅速提高的未来趋势，因此，被广泛投入作战使用［2］。而精准、快速、可靠地完成岸舰导弹作战单元的战场投送，也成为岸舰导弹作战运用的必然要求。

岸舰导弹作战单元（下称作战单元）的战场投送属于应急物资配送问题。近年来，随着自然灾害频发，局部武装冲突不断，国际社会对于该类问题给予了持续关注。应急物资配送问题表现为以下几大特征：一是灾情或战场形势持续演进使得用户需求和路网特征随时间不断发生变化；二是随着受灾面积或战场范围扩大，配送中心、需求点和应急物资种类增多，应急物资配送问题规模越来越大，解决起来越来越复杂；三是该问题要求在尽可能短的时间内以尽可能低的成本服务尽可能多的用户，是一个多目标决策过程。

针对以上特征，国内外许多学者进行了有益探索：针对特征1，陈达强等［3］结合汶川地震后医用物资分配实际特点，考虑了供应量、需求量的时变约束条件；陈丰等［4］以新冠肺炎暴发初期的医疗物资调度为研究对象，考虑了需求量的阶段性变化；Nulz等［5］在研究水资源的灾时分配时，考虑了路网的不确定性。针对特征2，庞海云等［6］在供求不对等的条件下，构建了有多个需求点和配送中心的物资分配决策模型；Barbarosoglu 等［7］建立了一种多品种物资、多种运输方式的两阶段随机规划模型；王妍妍等［8］构建了考虑多集散点、多配送中心和多受灾点的三级配送网络的应急物资多阶段分配模型。针对特征3，Tzeng 等［9］以最小化成本和配送时间，最大化满意度为目标，建立了多阶段应急物资配送模型；Chang 等［10］以需求的未满足率、配送时间和运输成本最小为优化目标，建立了多配送中心、多需求点配送模型；姜海洋等［11］基于复杂网络特性建立了运输网络节点风险评估模型，以运输时间最短和风险概率最低为优化目标，建立了运输路径多目标优化模型。

上述研究为开展作战单元投送问题研究提供了以下重点和方向：

1）在高技术战争条件下，敌方对我重要交通枢纽、交通运输线进行打击，将造成路网特征发生变化。根据不断变化的路网特征准确计算投送时间和风险，对于合理规划投送方案具有重要意义。

2）根据战前对敌情进行研判并制订的各阶段部署方案，确定各型作战单元的阶段性需求，并以该需求能否在特定时限内得到满足作为投送方案可否执行的约束条件，可以确保决策结果有利于各型武器系统作战能力的发挥。

3）对于多驻地、阵地，多型作战单元的多目标投送问题，寻求一种高效的多目标优化算法，可以有效提高决策的准确性和效率。

针对以上研究重点，第1 章构建了具有时变运输网络特征及动态需求的多型岸舰导弹作战单元投送决策模型；第2 章基于该模型和战场快速决策需要，设计了多目标优化算法；第3 章通过算例验证模型及算法的有效性。

1 问题描述及数学模型

1.1 问题描述

岸舰导弹作战单元由车辆搭载，运输方式以公路运输为主，在“驻地——发射阵地”两级调度体系下，各型岸舰导弹作战单元由驻地借由公路设施迅速转移至指定阵地，然后伺机发动攻击。在这一过程中，决策人员需要根据各驻地的装备数量条件、各阵地的实际作战需求，以及道路交通状况协调分配各型岸舰导弹作战单元，并形成合理、完善的调度方案。

战时条件下，作战单元投送以时效性和安全性为主要目标，既要保证作战单元及早抵达各阵地完成部署，又要规避敌方对主要交通路线实施打击造成通行延阻的风险。同时由于战场环境的复杂性，各条道路的通行时间和风险系数在不断发生改变。

各阵地的实际作战需求依据敌情变化适时作出调整，投送必须确保各作战单元运抵阵地时，阵地的实际作战需求得到满足。

本模型主要解决的问题是：确定各驻地向各阵地的各型作战单元分配量和各批作战单元起送时间，得到兼顾时效性和安全性的投送方案。

1.2 模型建立

1.2.1 模型假设

1）在组织作战单元投送前，已获取各道路路况信息（通行时间、风险系数及其变化情况）。

2）战前已针对敌情进行了分析和研判，并据此制订了不同时刻各阵地的实际作战需求。

3）各驻地可提供的各型作战单元数量已知。

1.2.2 参数和决策变量

1.2.3 建立模型

1）投送方案完成时间

2）系统总风险

采用系统总风险作为方案安全性的测度。由于运输网络中各条道路相互并联，一条道路被破坏不会导致其他道路无法通行，因此，不同作战单元通过各条道路的风险系数服从概率运算加法法则。可将系统总风险描述为：

目标函数式（1）为时效性目标，表示最小化投送完成时间；式（2）为安全性目标，表示最小化系统总风险；约束条件式（3）为需求约束，表示各阵地接收的各型作战单元数量应当满足tmax时刻各阵地对各型作战单元的需求；式（4）为供给约束，表示各驻地发出的各型作战单元数量不得超过各驻地的各型作战单元可供量；式（5）表示作战单元分配量应为非负整数；式（6）、式（7）为时间窗口约束，表示各作战单元的出发时间及投送方案的完成时间应当在任务起止时间区间内。

1.3 模型转化

时间依赖变量受连续时间系统的影响具有连续性，因而存在数据量过大、无法被计算机直接存取等问题。本节采取对连续时间系统进行离散化处理（即以较小的间隔Δ 将时间离散化，在每一段间隔里，认为时间依赖变量不发生改变）的方式，对模型作如下转化：

2 模型解算

在多目标优化问题中，目标之间存在相互制约的情况，优化一个目标可能会对其他目标造成损失。传统方法常常基于决策者的偏好，通过采取折中策略，将多目标合并为单一目标来解决该类问题。然而战场条件下，由于指挥员的偏好难以事先获知，因此，求得的解很难满足实际决策需要。

近年来，许多学者结合启发式算法，为多目标问题提供了新的求解思路［12-16］，这类算法可以提供多个具有不同特征的非劣解支持决策。但在算法运行过程中如何维护精英集、保证解的可行性等，仍然是运用该类算法解决多目标问题的难点［17］。本章针对模型特征，为了保证粒子在可行域内飞行，对初始化机制、更新策略进行改进；为了获取不同特征的非劣解，采取小生境策略进行适应度分配、维护精英集，提出了作战单元投送的多目标优化算法。

2.1 种群初始化

2.2 约束处理

在多目标优化问题中，对于约束条件的处理既要避免不可行解落入最终的非劣解集，又要避免初始群体不包含可行解，使进化过程停滞［18］。2.1 已经通过改进初始化机制保证了初始解的质量，因此，本部分主要通过将约束条件转化为目标函数惩罚项的方式，束紧非劣解集的准入条件。转化后的目标函数为：

在该函数中，粒子违反的约束条件越多、违反约束的程度越大，函数值就越大，从而使不可行粒子在与其他粒子的比较中受支配，进入精英集的可能性就越小。

2.3 精英集与适应度

在多目标优化问题中，存在一个折衷解（即非劣解，在至少一个目标上优于其他解）的集合，称为Pareto 最优解集（Pareto-Optimal Set）［19］，求解多目标问题实质上就是寻找或逼近这样一个解集，使得该解集能够支持不同偏好的决策者进行决策［20］。但由于决策者信息接受能力有限，一时间无法在过多的非劣解中作出选择，因此，必须使限定大小的解集包含拥有尽可能多的特征（该处所指特征即粒子对应的目标向量，下文同）的解。

基于以上考虑，本文采取精英保留策略，将每一次进化中产生的非劣解通过建立外部种群（精英集）保留下来，再根据粒子的聚集程度，采取小生境策略对精英集中的第n 个粒子分配适应度如下：

2.4 粒子更新策略

2.5 算法步骤

针对模型特点和实际决策需要改进后的算法可描述如下：

Step1 粒子初始化：按照2.1 的初始化机制初始化粒子位置，并随机生成初始粒子速度。初始位置作为粒子个体极值。

Step2 根据2.2 计算每个粒子对应的目标向量。

Step3 选取粒子群中的非劣解加入精英集并利用根据2.3 计算非劣解的适应度。

Step4 当迭代次数小于预设值maxgen 时，执行Step5～Step9，否则终止算法。

Step5 根据标准粒子群算法更新粒子位置和速度，并按照2.4 修正粒子位置。若修正后的粒子位置劣于其个体极值，则按5 豫的概率重新初始化该粒子。

Step6 重复Step2，选取粒子群中的非劣解加入精英集并剔除精英集中的劣解。

Step7 计算精英集中的粒子适应度，当精英集中的非劣解数量超过精英集容量SizeE 时，剔除适应度较小的非劣解粒子并重新计算剩余粒子的适应度。

Step8 采取与适应度成比例的轮盘赌方法选择全局极值。

Step9 更新个体极值：若当前粒子位置优于个体极值，则以当前粒子位置替换个体极值；若当前粒子位置既不优于也不劣于个体极值，按50 豫的概率以当前粒子位置替换个体极值。

Step10 输出非劣解集。

3 算例分析

3.1 战场想定

针对作战单元投送模型及其多目标优化算法，本节以某岸导部队作战调配为背景设计仿真试验。

某岸导部队驻扎于驻地1、2，两驻地的兵力配置条件为：驻地1 驻有A 型作战单元2 个，B 型作战单元1 个；驻地2 驻有A 型作战单元1 个，B 型作战单元1 个，兵员根据作战单元数量配备。两驻地可向5 个前沿阵地展开部署，驻地与阵地间运输网络参数按离散后，如表1 所示。

表1 运输网络参数的离散化结果

各阵地在不同时段的作战需求如表2 所示。

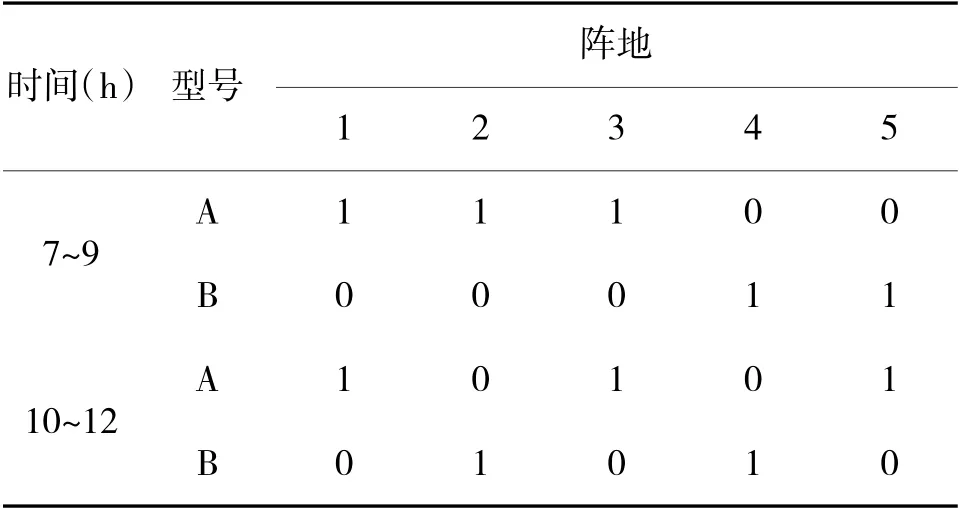
表2 前沿阵地的阶段性需求

现根据运输网络参数及各阵地作战需求设计投送方案，任务起止时间分别为7 h 和13 h。

3.2 仿真结果

表3 投送方案

其中，各作战单元的出发时间区间是表现为相同特征的解向量在相应位置上的元素的集合。

3.3 结果分析

为了验证本文算法的有效性，将所得结果与加权法及未改进的多目标粒子群算法进行比较。

运用加权法解算本文模型，为了消除不同量纲的目标值之间的不可加性，将多目标函数转化如下：

表4 加权法结果

将不同权重下加权法的结果与本文算法生成非劣解对应的目标函数值进行比较，如图1 所示。可以看出：方案1 对应的目标函数值与β1=0.8 时加权法的结果相等；方案6 对应的目标函数值与β1=0.2 时加权法的结果相等；而当β1介乎两者之间时，算法生成的非劣解要优于加权法的结果，并且生成的方案更多，为指挥员提供了更大的选择空间。说明设计的适应度分配及精英集维护策略是有效的。

图1 非劣解前沿与加权法结果对比图

运用未改进的多目标粒子群算法解算，并设定机制：若种群中无可行粒子，则对所有粒子进行变异（即重新初始化），记录变异次数。初始化阶段，种群进行了400 余次变异后产生了可行粒子；收敛速度上，由于产生的可行粒子数量过少，使得非劣解集达到饱和时的迭代次数高于改进后的算法，如图2 所示；粒子质量上，由于初始化阶段产生的若干可行粒子影响了后续粒子的更新，使得算法局部收敛，产生的非劣解均劣于改进后算法的非劣解。说明本文对于粒子初始化和粒子更新策略的改进是有效的。

图2 两种算法下精英集中粒子数量变化对比图

对比结果表明，算法在非劣解质量、算法收敛性等方面要优于加权法及未改进的多目标粒子群算法，更适合作战单元投送问题的求解及战时快速精准决策的需要。

4 结论

针对岸舰导弹作战单元快速响应部署作战任务，从作战单元战场投送的角度出发，考虑了供求约束、时间窗口约束等，以最小化投送完成时间和最小化系统总风险为目标，构建了多型、多供求点的作战单元投送决策模型，并设计了求解模型的多目标粒子群算法。模型的创新型在于：基于实际战场环境的复杂性，体现了运输网络的时变特征和作战需求的动态性；本文算法的创新性在于：1）通过设计粒子初始化和粒子更新策略，保证了粒子在可行空间内飞行；2）基于粒子聚集度设计了适应度分配策略，提高了非劣解集多样性。

仿真结果表明，本文模型及算法可以满足战时快速、精准决策的需要和作战单元投送任务需求。但本文对道路通行时间、风险系数等信息获取的工作还不够完善，下一步将考虑把道路交通枢纽作为运输网络节点加入模型，在寻求优化调度方案的同时规划出时长短、风险低的运输路径。