海上多无人机协同交叉定位的优化配置方法*

林晓烘，程志锋，于 莹，左 炜，田 威

（海军工程大学电子工程学院，武汉 430033）

0 引言

现代高技术海战中，对海上辐射源目标进行无源定位是获取敌方态势和引导武器打击的重要手段。无源定位技术利用多个侦察设备测量得到的辐射源电磁信号到达时间、到达角、信号幅度等参数实现目标定位［1-2］。其中，利用到达角信息进行测向交叉定位已成为近十年来受到广泛关注的研究领域。卢发兴等［3］推导出了多站测向交叉定位误差模型，深入分析了测量站数量和距离对定位精度的影响。宗军君等［4］提出了一种加权最大似然估计算法，克服了测向误差的标准方差随目标增加而增大的影响。罗双喜［5］重新定义了适用多站测向交叉的相对几何稀释度（RGDOP），给出了达到最优RGDOP 的条件和相应的测向站分布方法。

随着无人机技术的成熟，其在无源定位中应用越发受到重视［6］。Kutluyil［7］利用Fisher 信息矩阵的近似表示，将无人机航迹规划问题转换为一个非线性编程问题，通过求解定位的最小不确定度来获得每架无人机飞行路径上的位置。Koohifar 等［8］建立了Fisher 信息矩阵的预测模型，进而通过局部优化算法来求解路径规划问题。然而，这类方法的精度对无人机的飞行角度比较敏感。闫俊［9］利用总体最小二乘法和卡尔曼滤波算法来提高有色噪声背景下多机测向交叉定位的精度和收敛速度，然而该方法仅能用于既定飞行阵型和航迹。樊皓等［10］基于双机交叉定位的圆概率误差和动力学约束条件，建立了无人机双机协同定位的航迹规划模型，但该方法无法应用于3 部以上无人机的航迹规划问题。Wang W J 等基于深度神经网络算法实现对多部无人机协同交叉定位时各机飞机角度和距离进行优化配置［1］，然而，该方法需要先进行大量的线下训练，也未考虑无人机自身安全和通信等约束条件。

本文针对多无人机在满足安全、通信和动力学条件下，如何自动实时优化配置各机飞行角度和速度实现高精度定位展开研究。给出了多机协同测向交叉定位方法和精度评估指标，建立了动力学、通信距离和安全距离约束条件下无人机的优化配置模型，利用粒子群优化算法求解优化模型，获得下一时刻各机速度和飞行角度的配置值。

1 多无人机协同交叉定位原理

如图1 所示，假设海上编队发现前方有待定位的雷达辐射源目标H，其坐标为（xt，yt）；为更准确测量该辐射源的位置，海上编队通过舰船或者舰载飞机发射I 架电子对抗侦察无人机，在T 时刻，第i 架无人机坐标为（xi，T，yi，T），测得辐射源目标的方位为βi，T，则有下式［9］：

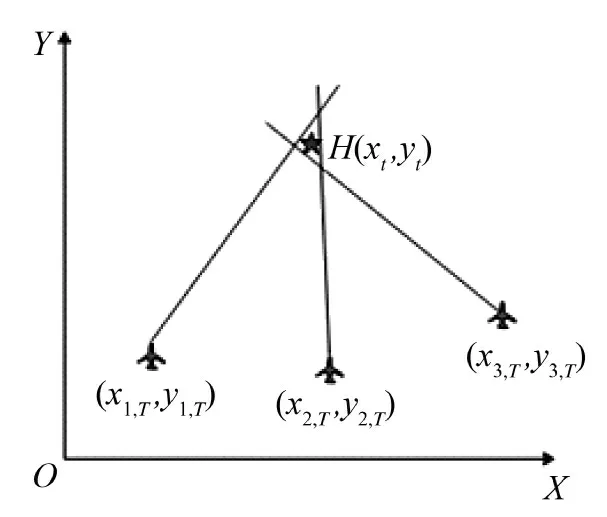
图1 多无人机协同交叉定位模型

式中，σx、σy为目标横坐标和纵坐标测量误差标准差，rxy为横纵坐标测量误差的相关系数。当无人机测向的测向误差较小时，可近似认为辐射源测量点散布区为一个椭圆。此时，可用几何稀释精度（Geometric Dilution of Positioning Accuracy，GDOP）来描述对目标的定位精度［11］。假设GDOP 表示为σr，其满足下式［3］：

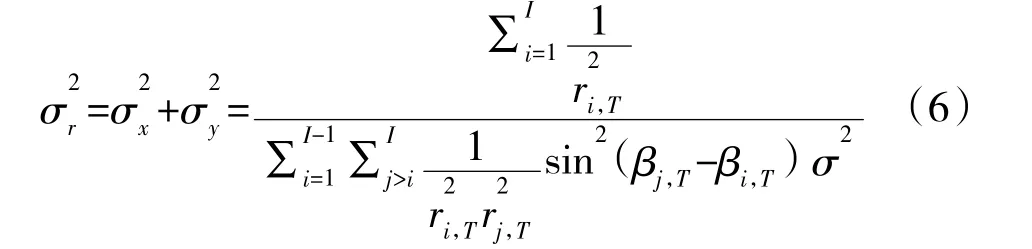
式中，ri，T表示T 时刻第i 架无人机与雷达辐射源目标之间的距离，σ2为无人机测向误差的方差。

2 多无人机优化配置方法

式中，Ts表示每个采样时刻对应的时间间隔。

无人机在飞行过程中，还受到多项因素约束。本文主要考虑动力学、通信距离和安全距离等3 方面影响。

2.1 动力学约束

无人机一般利用副翼和方向舵来实现转弯，由于惯性，无人机航向角受到一定的限制，一般用最大转弯角α 来描述，T+1 时刻第i 架无人机飞行角度受到下式约束：

2.2 通信距离约束

无人机在飞行过程中，需要和母舰或者飞机保持通联，因此，其前出距离还需满足下式：

2.3 安全距离约束

无人机前出侦察时，不能无限接近目标，为了避免被对方传感器发现或者火力打击，无人机与目标之间的距离不得小于R，此时有：

3 粒子群优化算法求解最优配置

由式（16）可知，优化配置问题的求解是一个带有约束条件的单目标优化问题。对于I 架无人机，共有2I 个变量，若用穷举全局寻优方法计算量随着精度急剧增加，若用梯度下降法等迭代方法则极易收敛至局部最优值。较为合适的方法是采用启发式优化方法，如粒子群算法、遗传算法、蚁群算法等。它们计算量较低又不易收敛于局部最优值。这些启发式算法中，粒子群优化算法具有收敛速度快、实现相对简单的优点，因此，本文采用粒子群优化算法来求解式（16）所描述的优化问题。

粒子群优化算法不能直接用来求解带有不等式约束条件的目标优化问题，可利用惩罚函数法将式（16）转换成无约束问题［12］，新的形式可表达为：

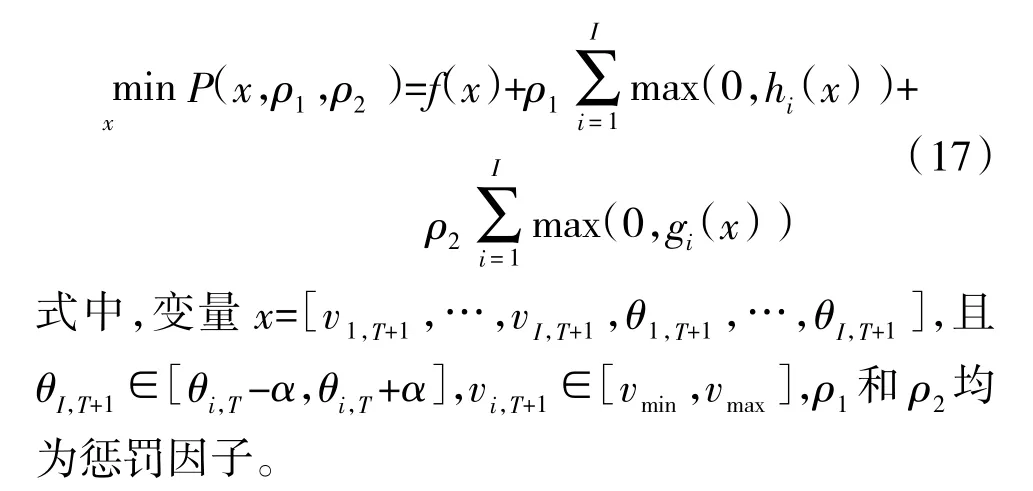
本文中，I 架无人机的优化配置问题即是一个具有2I 维变量优化问题。整个求解的过程可用图2表示。

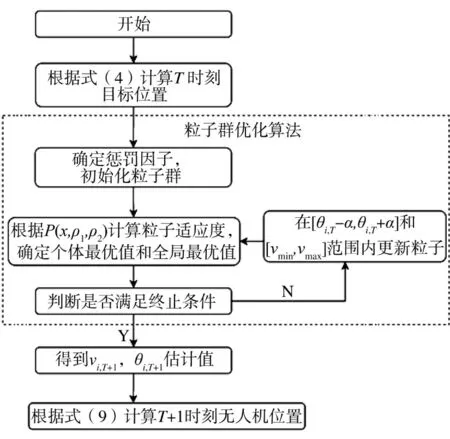
图2 本文算法流程图

1）假设当前时刻为T 时刻，可根据式（4）利用各无人机坐标和所测得的目标角度进行测向交叉定位，获得目标的位置估计值；

2）初始化粒子群，在［θi，T-α，θi，T+α］和［vmin，vmax］范围内生成N 个粒子的位置以及移动速度；

3）计算第i 个粒子xi的适应度值P（xi，ρ1，ρ2），将其中具有最小适应度值的粒子记作当次搜索中的个体极值pbest，将历次搜索中适应度最小值的粒子记为gbest；

4）根据下式更新第τ 次搜索的第i 个粒子速度和位置：

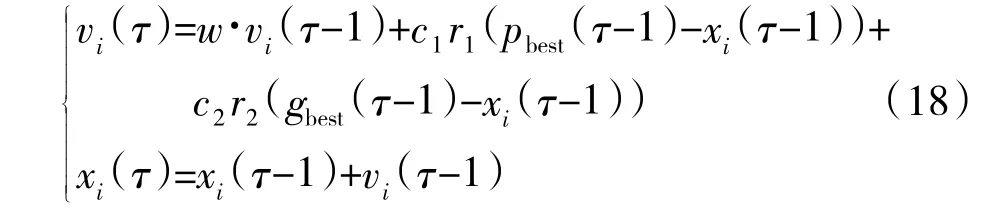
式中，w 为惯性权重系数，c1和c2分别为加速度因子，r1和r2均为［0，1］之间的随机数。判断粒子位置是否超出边界，若超出则重置粒子位置；

5）重复第3）～第5）步，直至满足粒子群迭代停止条件，将gbest作为T+1 时刻各无人机速度和飞行角度的估计值；

6）根据式（9）计算T+1 时刻的位置；

7）重复第1）～第6）步，直至达到预定的规划时间。

4 仿真试验与分析

假设以舰艇编队指挥舰位置为坐标原点，建立直角坐标系，编队发射3 部无人机协同侦察，机上电子侦察设备测向误差随机分布为满足［-1°，1°］的均匀，初始飞行速度为200 m/s，初始飞行方向均沿Y 轴正向；无人机与编队指挥舰的有效通信距离为90 km，为保证自身安全其与侦察目标的最短距离为10 km，飞行速度范围为100 m/s～300 m/s，单位时间内最大转弯角度为3°，仿真总步长300 步，每步间隔时间1 s。

4.1 对静止辐射源目标的协同定位

假设待定位辐射源目标固定不动，其坐标为（0 km，55 km）。针对本文算法和直线匀速飞行两种配置策略开展仿真，其中直线飞行策略不考虑无人机安全距离约束条件。考虑两种典型情况：一是无人机间距较小，以间距100 m 为例进行仿真；二是无人机间距较大，以10 km 为例进行仿真。下页图3 是利用本文优化配置方法所得到得无人机航迹图。由图可见，无人机首先会在角度上进行分离，使无人机相对目标视线夹角接近于90°，然后不断缩小与目标的距离，当达到安全距离后，各无人机会自动转向，以保证自身的隐蔽和安全。当无人机间距较小时，其中两部无人机的飞机轨迹非常接近，其视线均与另外一部无人机视线保持90°夹角，即使到达安全距离后，依然能够维持这种状态；当无人机间距较大时，其中一部无人机和另外两部无人机在角度上尽量分开，接近90°，但角度接近的两部无人机飞机轨迹不再重合，到达安全距离之后，3 部无人机自动转向，并向以目标为中心、3 部无人机成等边三角形状态过渡，此状态下定位精度最高。图4 为不同间距下本文优化配置方法与直线飞行策略在飞行过程中定位误差的对比图。由图可知，直线飞行策略定位误差缓慢下降，本文算法却能够通过角度分离快速达到较高的定位精度，随着与目标距离的接近，本文算法定位误差的减少趋势基本不变，但当无人机达到与目标安全距离时，由于无人机转向较大，定位误差略有上升，待状态稳定后，定位精度能够恢复到原先水平。由于直线运行策略不考虑安全距离，所以225 s 后，3 部无人机已突进对方打击圈，随着距离不断接近，其定位精度不断提高，所以在225 s 有部分时刻精度优于本文算法。值得一提的是，两种无人机阵型部署下本文方法最终定位误差都能收敛到100 m 左右的相近水平，这体现出本文优化配置方法对不同部署阵型的适应性。总体而言，在本文算法优化配置后，无论无人机间距大小，定位精度都能快速提高。

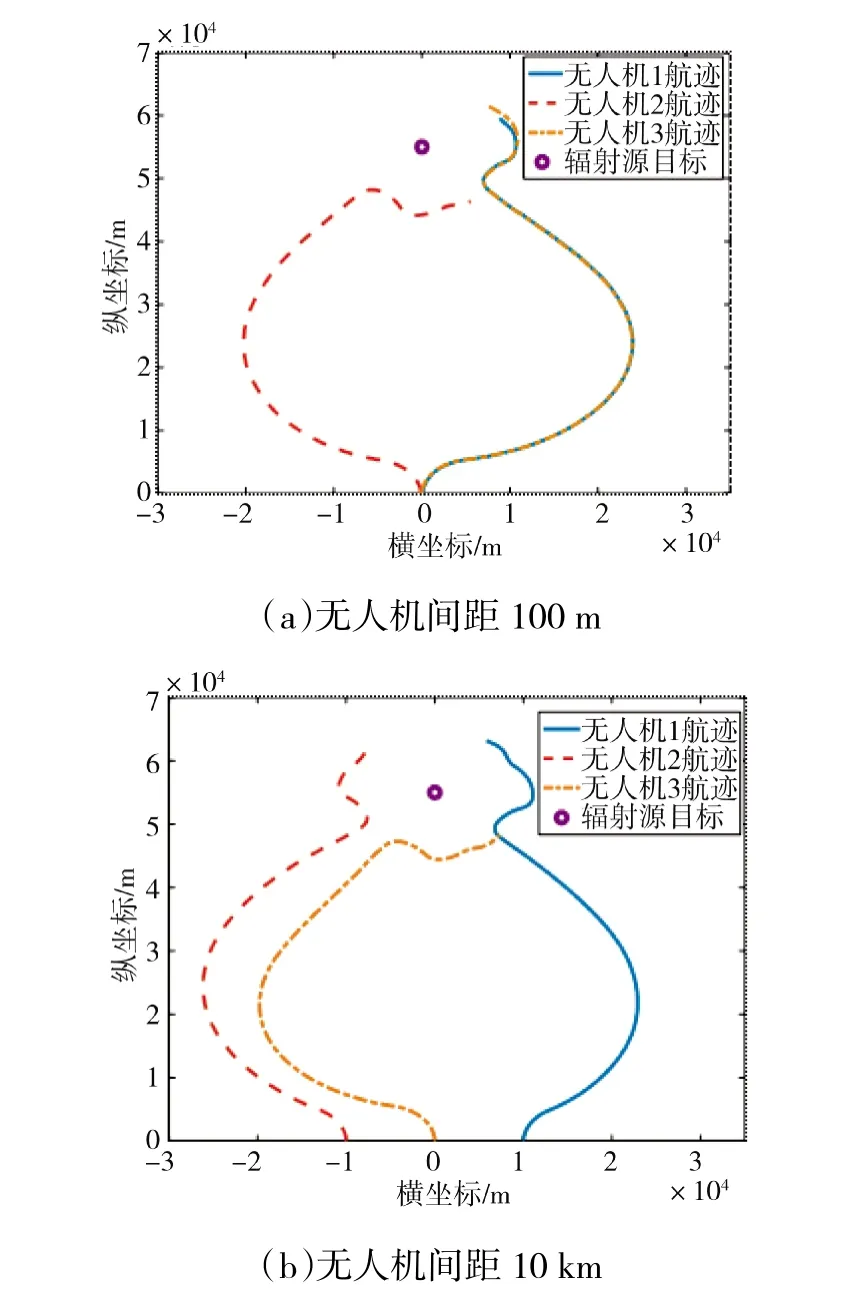
图3 辐射源目标静止时无人机航迹图

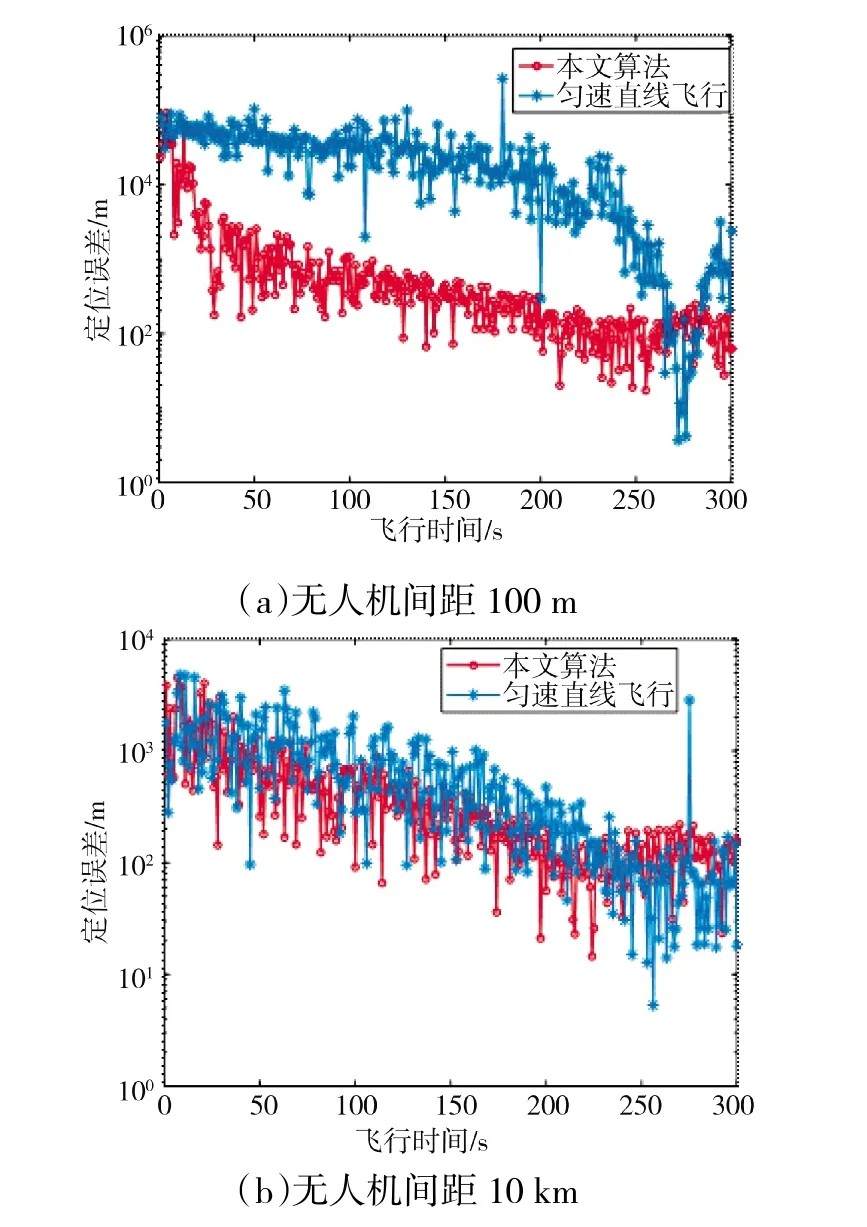
图4 本文算法与直线匀速飞行多无人机定位误差对比

4.2 对运动辐射源目标进行协同定位

分别针对慢速和快速运动辐射源目标展开仿真分析。

假设我方3 部无人机发射时初始间距为100 m，慢速辐射源目标初始位置为（0 km，55 km），其航向角30°，航行速度为16 m/s，此时3 部无人机航迹图如图5（a）所示。由图可知，虽然辐射源目标在缓慢移动，但本文算法也能适应性地调整飞行方向，使人机对辐射源目标的视线夹角接近90°，当无人机达到安全距离后，第1 部无人机和第2 部无人机沿相反方向飞行，使彼此与目标视线成等边三角形状态。

假设快速辐射源目标以45°方向角飞行，再平飞，最后以-135°方向角回返对我实施侦察，其飞行速度为250 m/s，此时3 部无人机航迹图如图5（b）所示。由图可见，3 部无人机依然先通过角度上的分离来提高定位精度，但是视线交角已经很难保持90°。这是由于辐射源目标速度较大，根据无人机前一时刻估计的最优解不再适用于当前时刻无人机位置，尤其是辐射源飞行方向和无人机基线方向平行时，前后两个时刻估计的目标方位和真实目标方位误差更大，此时协同定位的误差没有明显的下降。但总体而言，本文算法仍能使无人机自适应地调整彼此与目标视线交角，不断逼近目标，最后的估计精度依然能够达到百米量级。

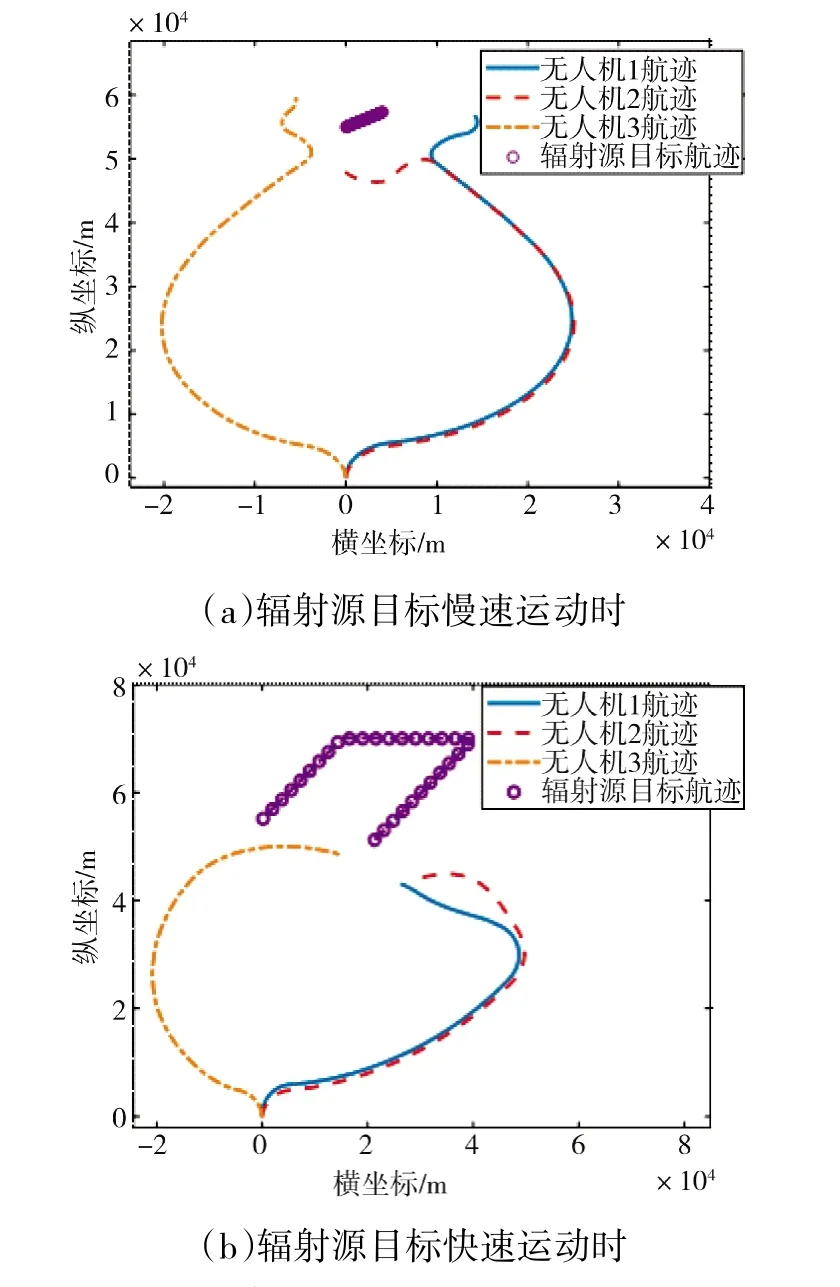
图5 辐射源目标运动时无人机航迹图

5 结论

无人机平台已成为当今电子对抗侦察的重要平台，如何使多部无人机在特定约束条件下实现自动优化配置运动参数，从而实现高精度定位是亟需解决的问题。本文基于多站测向交叉定位几何稀释精度，构建了无人机飞行速度和角度优化配置模型，该模型考虑了无人机安全距离、通信距离和动力学约束条件，提出了基于粒子群算法的优化模型求解方法和流程。本文优化配置方法对于不同的无人机阵型和辐射源运动状态都有较强的适应性，定位精度高，下一步将继续针对运动辐射源目标，考虑不同型号无人机协同和风力扰动等因素展开深入研究。