BTJ-5陀螺全站仪在轨道交通工程测量中的应用

桂维振 刘 阳 徐 强 司典浩

(1.北京工业职业技术学院 建筑与测绘工程学院，北京 100042； 2.山东水利职业学院，山东 日照 276286； 3.山东省地质测绘院，济南 250000； 4.北京市政建设集团有限公司，北京100164)

0 引言

随着城市的不断发展和人口的快速增长，城市轨道交通越来越重要，尤其是城市地下轨道交通因其客运量大、速度快、不占用地面空间的优势，成为很多城市解决交通问题的首选[1]。城市轨道交通隧道内多采用导线测量建立平面控制网，因受隧道空间的限制，导线多为直伸型，随着隧道的开挖，因缺少足够的检核条件，导致导线精度越来越低，积累的误差越来越大[2]。

陀螺全站仪定向为物理定向，不受几何定向的投向误差影响，因此可以对洞内导线进行检核与修正，以提高控制网的精度。当贯通导线很长时，在适当的位置加测陀螺定向边用于导线检查，可以避免导线误差积累，大大提高隧道贯通精度。

1 BTJ-5型陀螺全站仪简介

BTJ-5型陀螺全站仪是航天科技集团十五所自主研发生产的定向设备，如图1所示。

该仪器为下架式陀螺全站仪，上置Leica生产的TS-06plus 1″全站仪。其能耗低、操作简单、定向速度快、定向精度高，不受地理环境、外界磁场的影响，实现了全自动陀螺定向，寻北精度高达5″。

2 陀螺全站仪定向原理及计算

2.1 定向原理

陀螺仪内绕其对称轴高速旋转的陀螺具有2个重要特性，(1)定轴性。即在没有外力矩的作用下，陀螺转轴的方向始终指向初始恒定方向。(2)进动性。即在外力矩的作用下，陀螺转轴产生进动，沿最短路程向外力矩的旋转轴所在铅垂面靠拢，直到2轴处于同一铅垂面为止。

当陀螺仪的陀螺高速旋转，其转轴不在地面真子午线的铅垂面内时，陀螺转轴在地球自转的力矩作用下产生进动，向真子午线和地球自转轴所在的铅垂面靠近，于是陀螺的转轴就可以自动地指示出真北方向。高速旋转的自由陀螺的转轴在惯性作用下不会静止在真北方向，而是在真北方向左右摆动。

2.2 仪器常数

由于陀螺仪存在生产公差，所以陀螺仪轴的稳定位置通常不与地理子午线重合，二者的夹角称为仪器常数，一般用Δ表示。如果陀螺仪子午线位于地理子午线的东边，Δ为正；反之，则为负。仪器常数Δ可以根据已知控制点方位角直接测得，两者关系如图2所示[3]。

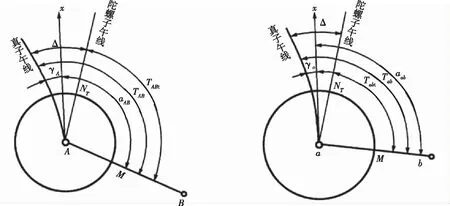
(a)地面已知边仪器常数测定 (b)地下待测边坐标方位角求算图2 仪器常数示意图

2.3 定向边方位角计算

由图2(b)可推算出地下定向边ab的坐标方位角

αab=Tab-γ0=Tabt+Δ-γ0

(1)

Δ=TAB-TABt=αAB+γA-TABt

(2)

式(1)中，αab为地下定向边的坐标方位角；Tab为地下定向边的真方位角；Tabt为地下定向边的陀螺方位角；Δ为陀螺仪仪器常数；γ0为a点的子午线收敛角。

式(2)中，TAB为地面已知边的真方位角；TABt为地面已知边的陀螺方位角；αAB为地面已知边的坐标方位角；γA为A点的子午线收敛角。

将式(2)代入式(1)得出

αab=αAB+(Tabt-TABt)+(γA-γ0)=

αAB+(Tabt-TABt)+δγ

(3)

由δγ=(γA-γ0)为地面与地下测站点的子午线收敛角的差值，得出

δγ=μ(YA-Ya)

(4)

式(4)中，δγ以(′)为单位，μ=32.3tanφ(s/km)；μ为计算子午线收敛角插值的系数。则有

δγ=32.3tanφ(YA-Ya)

(5)

式(5)中，φ为当地纬度；YA为地面设站点的横坐标，km；Ya为地下设站点的横坐标，km。

3 定向流程

本次定向位于广州市11号线天河公园站―华景路站，盾构区间主要位于天河公园内。陀螺定向采用交接桩资料提供的精密导线控制点XXIJ007，XXIJ005，在右线隧道内布设1条待测边YX8—YX9，对盾构区间右线进行待测边陀螺定向观测。以XXIJ007—XXIJ005作为地面控制边，进行3次陀螺方位角观测，再到待测边YX8—YX9进行3次陀螺方位角观测，最后复测XXIJ007—XXIJ005控制边3次陀螺方位角。根据陀螺方位角与坐标方位角的转换计算，解算出隧道内定向边坐标方位角，将计算结果与采用全站仪导线测量方法所得结果进行比较，以评定地下控制导线定向精度的可靠性。

按照《城市轨道交通工程测量规范》(GB/T 50308-2017)的规定：(1)地面已知边、地下定向边的陀螺方位角测量每次应该三测回，测回间陀螺方位角较差应小于20″；(2)测前、测后各三测回测定的陀螺仪常数平均值的较差应小于15″[4]。

3.1 地面控制边及地下待测边坐标数据检核

为更好地进行隧道内待测边的陀螺定向，选择测量精度高、观测条件稳定的地面已知点架设仪器。地面已知控制点为委托方提供的GNSS控制点XXIJ007，XXIJ005，委托方同时提供了隧道内利用导线观测的待测点YX8，YX9，以便计算子午线收敛角差值及对比定向结果。坐标数据如表1所示。

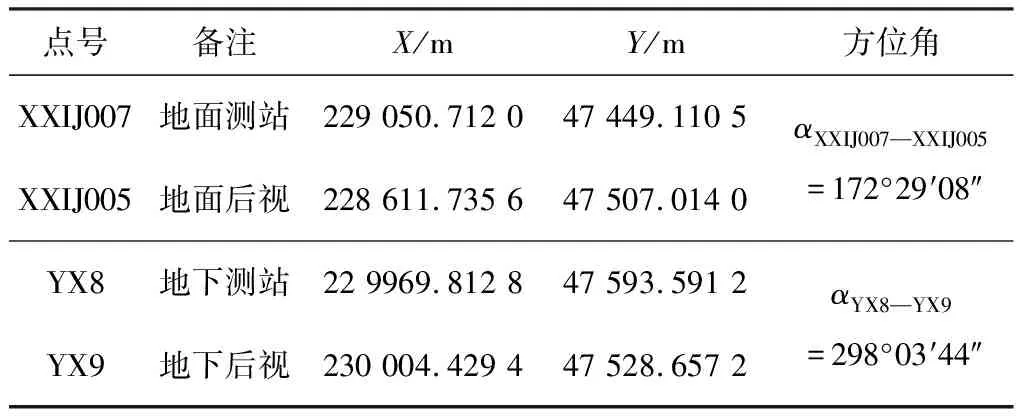
表1 地面控制点及地下定向边坐标成果表

3.2 地面控制边陀螺方位角测量

控制点坐标方位角计算完毕，开始首测地面控制边。地面控制边XXIJ007—XXIJ005陀螺定向观测结果如表2所示。

表2 地面控制边XXIJ007—XXIJ005陀螺观测取值计算表

各测回间较差限差20″，陀螺方位角平均值中误差限差±5″。由表2可知，本次中误差±1.0″，TABt=172°30′32″,根据复测结果计算陀螺仪常数平均值Δ较差为0″，表明仪器稳定、精度可靠。

3.3 地下待测边陀螺方位角测量

地面控制点首测后进行井下右线隧道地下待测边观测。地下待测边YX8—YX9陀螺定向观测结果如表3所示。

表3 地下待测边YX8—YX9陀螺观测取值计算表

3.4 陀螺定向边坐标方位角计算

根据方位角计算式(3)可得，右线隧道待测边YX8—YX9陀螺定向计算坐标方位角：

αab=αAB+(Tabt-TABt)+δγ=172°29′08″+(298°05′04″-172°30′32″)+32.3×tan 23°×(47 449.110 5-47 593.591 2)/1 000=172°29′08″+(298°05′04″-172°30′32″)-0°0′02″=298°03′38″

3.5 定向成果对比

表1已有地下定向边按导线计算得出的坐标方位角，通过与陀螺定向测量计算得到的坐标方位角进行对比，对比结果如表4所示，两者差值6″，满足规范要求。

表4 陀螺定向计算与控制点计算坐标方位角对比

4 精度分析

4.1 一次测定中误差

本次定向测量可由白赛尔公式(6)求算陀螺方位角一次测定中误差

(6)

陀螺仪全站仪在地面已知边的一次测定中误差

(7)

陀螺仪全站仪在地下定向边的一次测定中误差：

(8)

式(6)～式(8)中，[vv]为仪器常数与各次仪器常数差值的平方和；v为仪器常数的平均值与各次仪器常数的差值；n为测回数，取ns=6，取nx=3。

4.2 一次定向中误差

陀螺定向边的坐标方位角αab=Tabt+Δ-γ0

一次测定中误差计算由误差传播定律得

(9)

式(9)中，mTabtp为待测边陀螺方位角平均值中误差；mΔp为仪器常数平均值中误差；mγ为子午线收敛角的中误差。

因子午线收敛角的误差较小，可忽略不计，故式(9)可写为

(10)

又因为地面、地下都采用同一台仪器，使用同一种观测方法，由同一观测者操作，则可认为地面、地下一次测定陀螺方位角的条件大致相同，所以可取mΔp=mTABtp[5]。

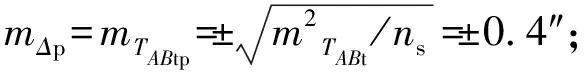
所以一次定向中误差为

5 结论

通过上述分析可知，仪器常数的确定与地面已知边坐标方位角有关，所以应选取较高精度的地面已知边。

高精度全自动陀螺全站仪通过对洞内导线进行定向检核，可以保证洞内长距离导线的准确性。《城市轨道交通工程测量规范》(GB/T 50308-2017)中要求，隧道单向贯通距离大于1 500 m时，应通过采用在隧道内加测陀螺方位角等方法提高控制网精度。本文研究可为陀螺全站仪在相关领域的工程应用提供一定的技术参考。