钢钉数量对托盘弯曲力学性能的影响

巩桂芬，刘随强，田洋洋

钢钉数量对托盘弯曲力学性能的影响

巩桂芬a,b,c，刘随强a,b,c，田洋洋a,b,c

（陕西科技大学 a.陕西省造纸技术与特种纸品开发重点研究室 b.中国轻工业纸基功能材料重点实验室 c.轻化工程国家级实验教学示范中心，西安 710021）

确定能够满足托盘安全使用需求时的钢钉数量。通过Iron CAD三维建模软件建立不同钢钉数量的托盘模型。利用Ansys Workbench软件对1—5颗钢钉数量的托盘进行有限元仿真分析，再通过托盘抗弯强度试验，得到其实际变形量，并对有限元结果与试验结果进行对比分析。在3.5 kN载荷下，托盘的最大弯曲变形在不断减小。有限元结果表明，托盘最大变形量1颗钉为48.624 mm，2颗钉为46.139 mm，3颗钉为38.740 mm，4颗钉为25.280 mm，5颗钉为22.899 mm。试验结果表明，托盘最大变形量1颗钉为46.654 mm，2颗钉为43.572 mm，3颗钉为36.344 mm，4颗钉为30.697 mm，5颗钉为27.273 mm。试验结果与有限元结果趋势相同，验证了仿真的可靠性。随着钢钉数量的不断增多，胶合板托盘的抗弯能力在不断增强，当钢钉数量达到4颗后，即可满足托盘的安全使用需求。

钢钉数量；托盘；抗弯强度；有限元分析；弯曲变形

托盘是商品流通中最基本的集装单元，它能够极大地提高货物的装卸搬运效率与运输包装的安全性[1—3]。托盘在实际工况下承受的弯曲载荷主要来自静态堆码与叉举等工况。木托盘的抗弯强度又与托盘使用的材质、截面尺寸、连接方式等因素有关[4—6]。一直以来，工程师对于托盘的设计仅仅去考虑材质和尺寸，钢钉数量仅依靠工人生产经验来决定。通过研究钢钉数量对托盘的抗弯强度的影响，既可以降低托盘的生产成本，又提高托盘的抗弯强度和生产效率，这对于托盘的实际应用具有一定的指导意义。

国内外诸多学者做了托盘的研究，国内许淳等[7]建立了小径木通用平托盘在均布载荷及集中载荷不同作业情况下的力学模型，并进行抗弯试验。曹菲[8]对木托盘静载堆码时的力学性能进行了理论分析和有限元模拟。巩桂芬、李毅等[9]确认OSB板托盘的实用性，并且发现钢钉的钉间距会对托盘的抗弯强度产生一定的影响。国外WASEEM A等[10]使用Ansys对不同材料托盘进行了对比分析。BERNUZZI C等[11]通过有限元软件对钢制托盘的强度进行了有限元仿真分析。这些学者的分析，促进了有限元分析在托盘弯曲变形的应用，但是在上述研究中，是将托盘部件之间的连接为一个整体。在实际中，托盘部件之间的连接是通过钢钉连接，钢钉数量的不同，也直接对托盘的强度有影响，因此文中通过钢钉模型连接托盘各个部件，来探究不同布钉数量对胶合板抗弯强度的影响，使仿真分析更加接近实际应用。

1 握钉力测定

1.1 材料与设备

主要材料：胶合板与螺纹钢钉，胶合板采用山东曹县盛鹿木业有限公司生产的胶合板，螺纹钢钉采用肇庆展丰五金制品有限公司45 mm长的螺钉。

主要仪器：深圳三思纵横科技股份有限公司生产的UTM5305电子万能试验机。

1.2 方法

试验根据GB/T 17657—2013，GB/T 14018—2009中人造板材握钉力的测定方法[12—13]，对普通胶合板和螺纹钢钉的握钉力进行测定。将不同厚度的胶合板钉用胶粘合，然后制作成为75 mm×50 mm×50 mm的样品，共制作7个样品，将螺纹钢钉均匀钉入样品深度为30 mm，然后将胶合板放置在夹具内，用夹具夹紧螺钉，握钉力试验见图1，试验机以20 mm/min的速度匀速上升，直至钉子拔出。胶合板握钉力试验结果见图2。

由图2可知，胶合板的握钉力为600～1000 N，握钉力计算见式（1）。

图1 胶合板握钉力试验

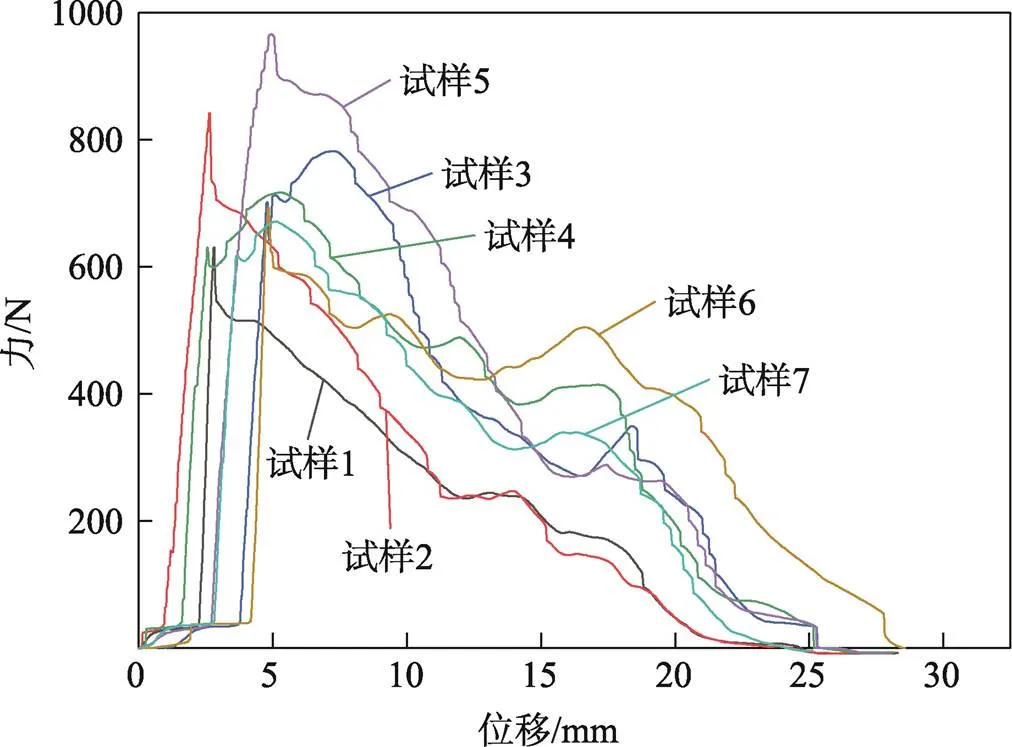
图2 胶合板握钉力试验结果

(1)

式中：ap为握钉力；max为最大拉力；为打钉深度。

经过计算，握钉力ap=25.23 N/mm。

2 弹性薄板弯曲变形理论

托盘由7根顶铺板组成，取其中一根进行分析，在弹性力学薄板理论中，将厚度尺寸远小于其余2个尺寸的构件称为薄板，根据板材厚度相较于其他2个方向的尺寸比例，可以将板分成3种情况：薄膜、薄板、中厚板，顶铺板属于薄板[14]。

根据薄板弯曲变形理论中莱维解法[15]，设薄板的两对边=0，=为简支，其余两边为任意边界，承受任意载荷，将薄板弯曲挠度设定为单三角级数，见式（2）。

(2)

(3)

将式（2）代入式（3）可得：

(4)

(5)

代入式（4），可得出：

(6)

方程（6）的解可表示为：

(7)

式中：f()为方程（6）的任意特解；A，B，C，D为待定常数，取决于两边的边界条件。将式（7）代入式（2）中，即可得弹性薄板的挠度变形表达式为：

(8)

3 胶合板托盘建模与有限元分析

3.1 胶合板托盘建模

胶合板托盘结构见图3，胶合板托盘是由顶铺板，纵梁，垫块，底铺板等4部分组成，文中所描述胶合板托盘为单面使用四向进叉托盘，尺寸为GB/T 2934—2007[16]中所规定的1200 mm×1000 mm，托盘各构件尺寸具体见表1托盘构件参数。托盘各部件之间连接采用钢钉连接，钢钉连接模型见图4。托盘材料为普通胶合板材料，所有钢钉为普通钢钉，经测得胶合板和钢钉的材料参数见表2[17]。

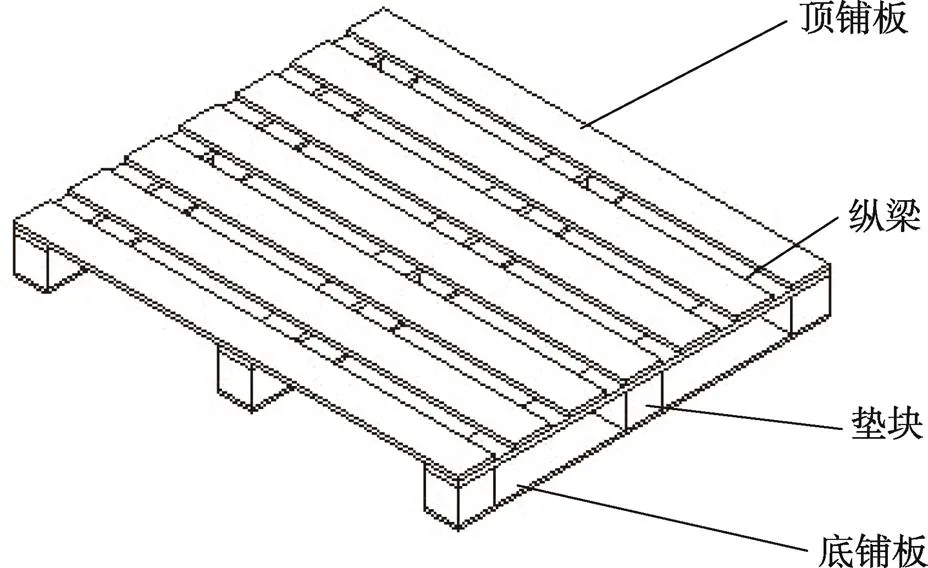
图3 托盘结构

表1 托盘构件参数

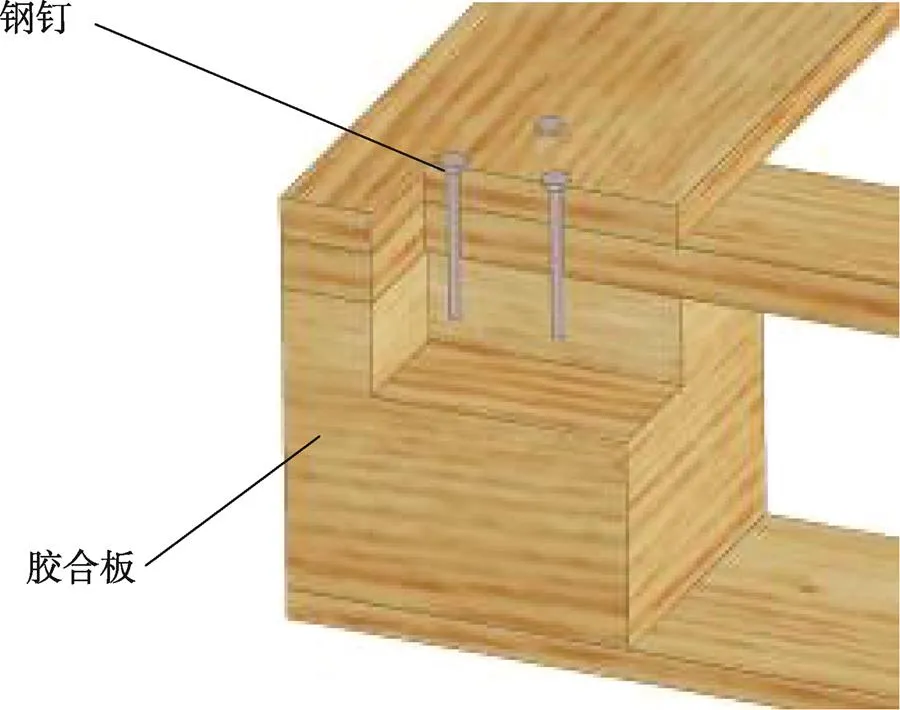
图4 托盘钢钉连接模型

3.2 托盘的有限元分析

利用三维建模软件Iron CAD建立单面使用四向进叉托盘模型，分别使用1—5颗钢钉来连接顶铺板与垫块，钢钉排布采用实际应用中常规排布方式，具体的钢钉排布状态见图5。其中1—3颗钉对托盘整体进行有限元仿真分析，4—5颗钉对托盘局部进行仿真分析，将建立好的托盘模型导出X­_T格式。在Ansys Workbench中选取静力学模块，将Iron CAD建立好的模型导入Ansys Workbench中。根据GB/T 4996—2014《联运通用平托盘试验方法》[18]中托盘抗弯试验要求，对胶合板托盘的抗弯强度试验进行有限元仿真分析。

网格划分采用六面体网格划分方法，其中顶铺板与纵梁尺寸设置为15 mm，木墩与底铺板尺寸设置为25 mm，共生成31 838个单元，119 267个节点，托盘有限元模型见图6。

确定实际使用弯曲载荷为3.5 kN，托盘顶部是由7根顶铺板组成，因此，每根顶铺板受力为500 N，在局部托盘仿真中施加载荷为500 N。接触设置，在其他有关文献中，将钢钉与木块之间的连接设置为绑定接触，或者直接将顶铺板与纵梁、木墩之间的接触设置为绑定接触，这种连接是使得托盘各个部件之间不会出现相对滑动，不符合托盘实际使用情况[5,8—9]。而在实际中，托盘各部件的连接是依靠钢钉连接的，而且当出现弯曲载荷过大时，钢钉会与木墩，纵梁之间出现相对位置的滑动，因此在此次仿真试验中，将胶合板各部件之间的接触设置为摩擦接触，摩擦因数为0.2。将钢钉与胶合板之间的设置为摩擦接触，根据GB/T 17657—2013和GB/T 14018—2009中握钉力计算公式，钢钉与托盘各部件之间的摩擦力为钢钉与胶合板的接触厚度与握钉力的乘积，见式（1）[12—13,19]。单个钢钉与托盘各部件之间的摩擦力见表3，不同钢钉数量所对应的具体摩擦力见表4。

表2 胶合板与钢钉材料参数

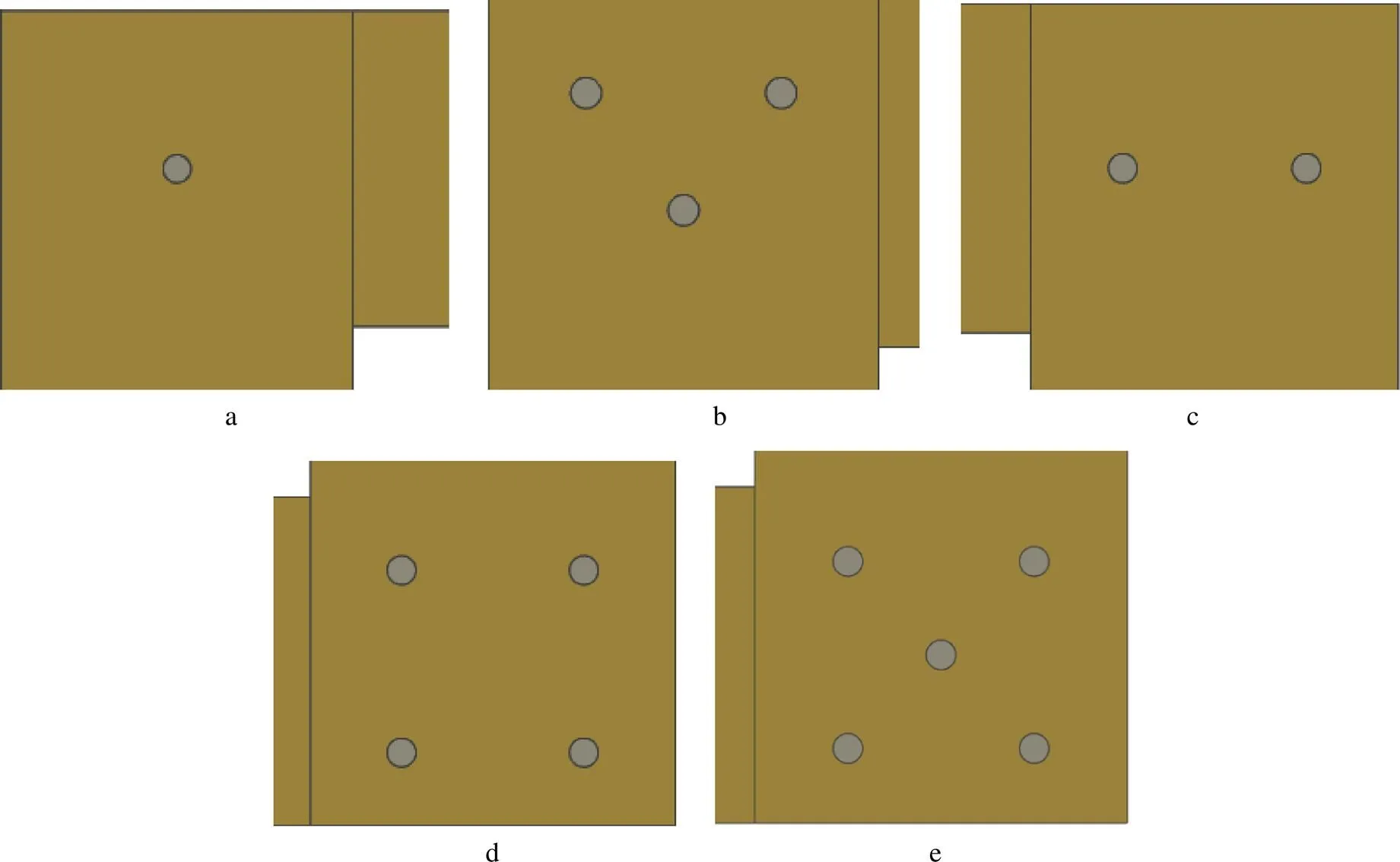
图5 钢钉排布状态

图6 托盘有限元模型

表3 单个钢钉与托盘不同部件之间的摩擦力

表4 不同数量钢钉所对应的摩擦力

3.3 结果分析

不同钢钉数量下在施加3.5 kN力的作用下，托盘的位移变形云图见图7。由图7a可知，当钢钉的数量为1颗时，托盘的最大变形为48.624 mm，最大变形量位置发生在托盘的中间位置，由于钢钉数量的不足，顶铺板边缘与纵梁之间出现了间隙。由图7b可知，当连接钢钉数量变为2颗时，托盘的最大变形量为46.139 mm，与1颗钉的位移相差不大。由图7c，7d，7e可知，当钢钉数量逐渐由2颗递增到4颗时，托盘最大变形量由46.139 mm递减到25.280 mm变形逐渐减小。由图7e可知，当钢钉数量由5颗时，托盘最大变形量由46.139 mm。递减到22.899 mm，变形趋势逐渐减小，当钢钉数量由4颗增加为5颗时，托盘的最大变形趋势变缓，此时可得出当钢钉数量为4颗时即可满足托盘的安全使用需求。

4 托盘抗弯强度试验

4.1 材料与设备

主要材料：胶合板与螺纹钢钉，胶合板采用山东曹县盛鹿木业有限公司生产的胶合板，螺纹钢钉采用由肇庆展丰五金制品有限公司生产的螺钉。

主要仪器：东莞市华泓仪器有限公司生产的HH-BC03压力试验机。

4.2 试验方法

根据GB/T 4996—2014 《联运通用平托盘试验方法》[18]中托盘抗弯强度的要求，分别对1—5颗钉的局部托盘进行抗弯试验，试验样品按照仿真中钢钉排布方式进行排布。将托盘放置在下压板上，托盘两端放置支撑块，在托盘顶铺板上距边183 mm处放置2块截面50 mm×50 mm的木块，来模拟加载杠。然后以5 mm/min的速度施加压力，直至压力值达到额定压力500 N，试验见图8。

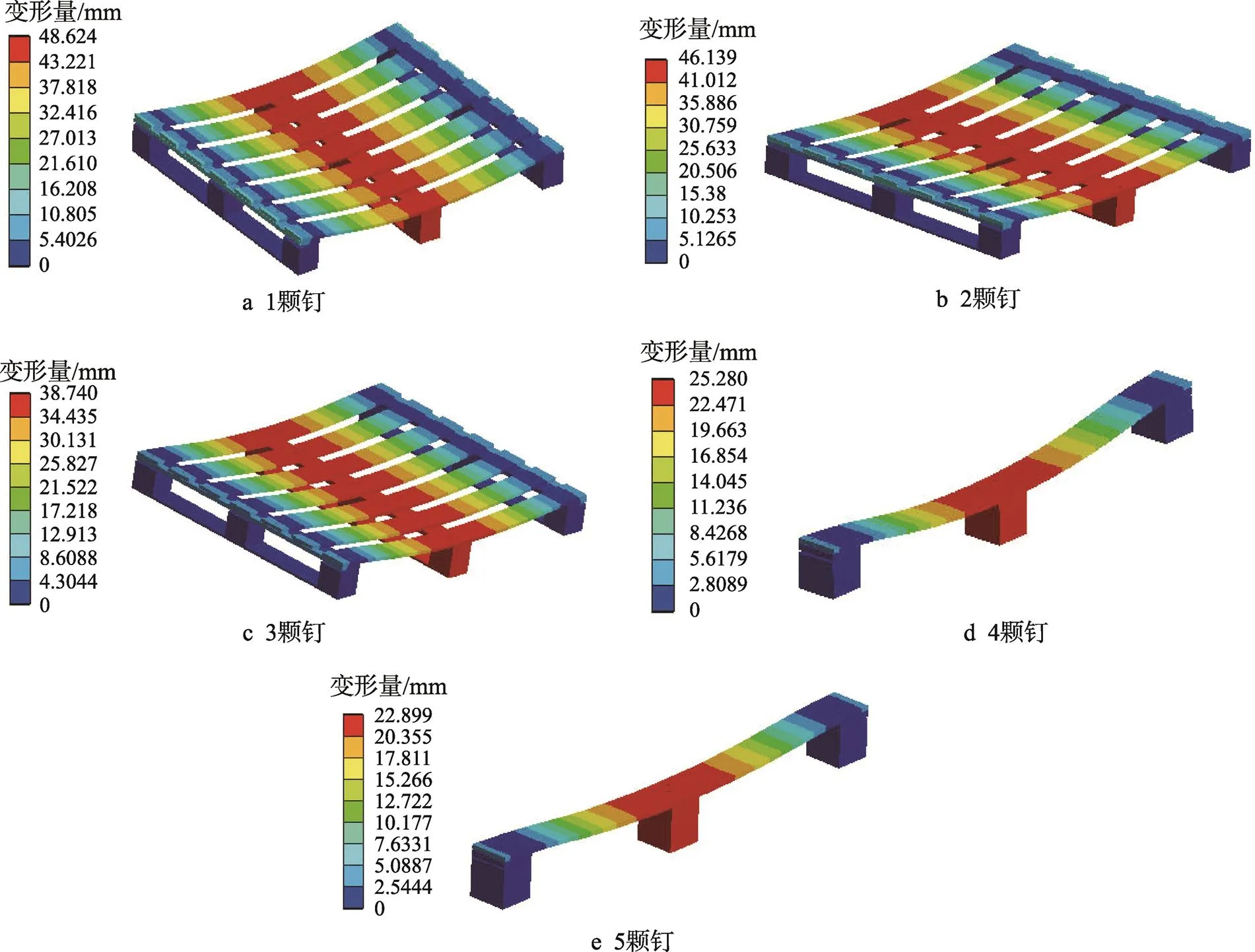
图7 不同钢钉数量托盘位移云图

图8 不同钢钉数量托盘抗弯试验

4.3 结果分析

由图9可知，试验结果与有限元结果相近，托盘的最大变形量随着钢钉数量的增多而减小。1颗钉托盘的变形最大，最大变形量为46.652 mm，当钢钉数量为2颗，托盘的最大变形量为43.572 mm，3颗钉托盘实际最大变形量为36.344 mm，4颗钉托盘实际最大变形量为30.697 mm，5颗钉最大变形量为27.273 mm。当钢钉数量由1颗增加到2颗时，托盘的最大变形量变化较小；当钢钉数量由2颗增加到4颗时，钢钉数量对托盘变形的影响较大，托盘的最大变形量变化较大；当钢钉数量大于4颗后，托盘变形变化较小，此时影响托盘的抗弯强度为制作托盘本身的材料，因此当钢钉数量达到4颗后即可满足托盘部件之间的安全使用需求。

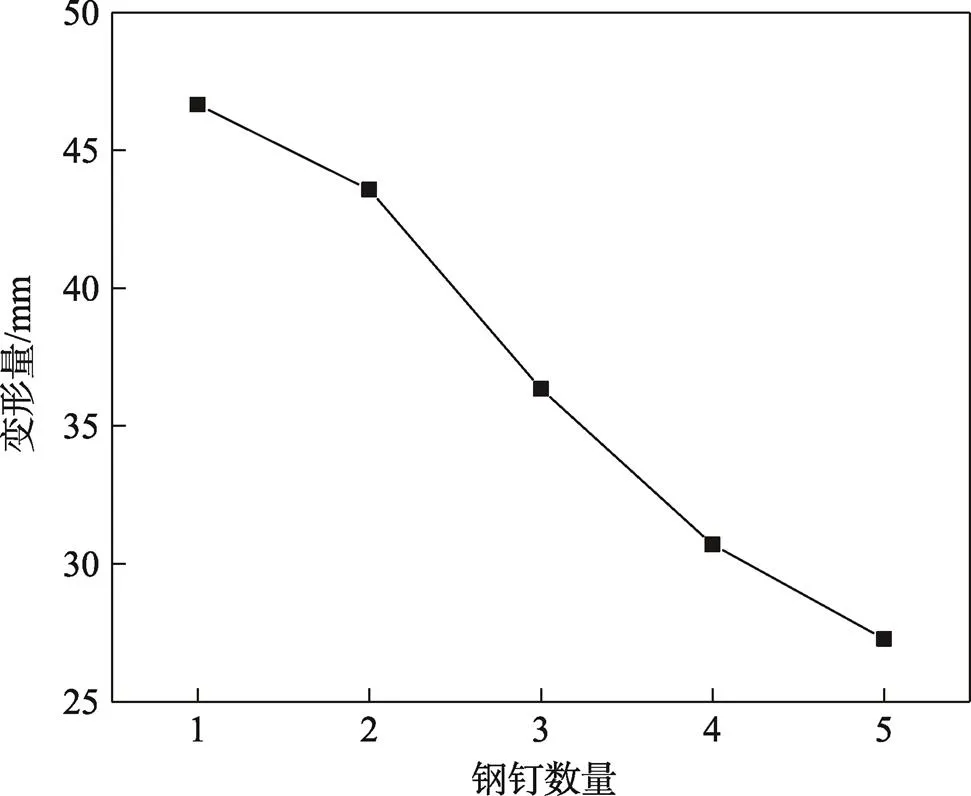
图9 不同钢钉数量托盘最大变形量

5 试验结果与有限元结果分析

由图10可知，当托盘的载荷达到3.5 kN时，试验结果为1颗钉托盘变形最大，最大为46.652 mm，由有限元仿真得出1颗钉托盘最大变形量为48.624 mm，两者相差1.972 mm，有限元与试验的误差为4.2%。当钢钉数量为5颗时，托盘的变形最小，托盘的实际变形量为27.273 mm，有限元仿真结果5颗钉托盘的最大变形量为22.899 mm，两者之间相差4.374 mm，总体试验结果与有限元结果之间误差较小，趋势相同。考虑到同种材料性能之间的差异性，托盘在制作过程中的一些误差，以及试验过程与试验设备精度引起的误差，总体上局部托盘的试验结果与仿真结果接近，以此验证了仿真结果的可靠性。

图10 托盘试验与有限元变形结果对比

6 结语

通过试验的方法测得普通胶合板对钢钉的握钉力，在有限元仿真过程中，将托盘各个部件的连接采用摩擦接触，使得仿真更加贴近托盘的实际应用。通过利用Ansys Workbench软件对不同钢钉数量的托盘进行仿真，得到在3.5 kN的载荷下，随着钢钉数量的增多，托盘的最大变形在不断减小，当钢钉数量达到4颗后，托盘的变形趋势变化较小，此时即可满足托盘的安全使用需求。在有限元仿真中1颗钉托盘的最大变形量为48.624 mm，5颗钉托盘的最大变形量为22.899 mm；通过试验，1颗钉托盘最大变形量为46.652 mm，5颗钉托盘的最大变形量为27.273 mm，试验与有限元仿真结果相近，验证了仿真的可靠性，为今后在托盘的设计方面提供了一定的参考。

[1] 杨世军, 杨学春, 尤浩田. 木托盘的发展前景及存在的问题研究[J]. 森林工程, 2013, 29(2): 135-138.

YANG Shi-jun, YANG Xue-chun, YOU Hao-tian. Research on the Development Prospects and Existing Problems of Wooden Pallets[J]. Forest Engineering, 2013, 29(2): 135-138.

[2] 吴清一. 中国托盘手册[M]. 北京: 中国财富出版社, 2014: 137-140.

WU Qing-yi. China Pallet Handbook[M]. Beijing: China Fortune Press, 2014: 137-140.

[3] 杨世军. 热处理条件下柞木托盘构件力学特性的研究[D]. 哈尔滨: 东北林业大学, 2014: 1-6

YANG Shi-jun. Study on the Mechanical Properties of Oak Pallets under Heat Treatment[D]. Harbin: Northeast Forestry University, 2014: 1-6

[4] 彭国勋. 物流运输包装设计[M]. 北京: 文化发展出版社, 2012: 320-330.

PENG Guo-xun. Logistics and Transportation Packaging Design[M]. Beijing: Printing Industry Press, 2012: 320-330.

[5] 巩桂芬, 李毅, 孔腾华. 托盘货架载荷仿真及计算公式推导[J]. 物流科技, 2018, 41(1): 65-67.

GONG Gui-fen, LI Yi, KONG Teng-hua. Pallet Rack Load Simulation and Calculation Formula Derivation[J]. Logistics Technology, 2018, 41(1): 65-67.

[6] 黄志明, 石城鑫, 刘雷业, 等. 基于PLC的纸托盘控制系统设计[J]. 现代制造技术与装备, 2021, 57(6): 184-185.

HUANG Zhi-ming, SHI Cheng-xin, LIU Lei-ye, et al. Design of a Paper Pallet Control System based on PLC[J]. Modern Manufacturing Technology and Equipment, 2021, 57(6): 184-185.

[7] 徐淳, 庞燕. 新型小径木通用平托盘力学性能理论研究[J]. 中南林业科技大学学报, 2017, 37(8): 135-138.

XU Chun, PANG Yan. Theoretical Study on the Mechanical Properties of a New Type of Small Diameter Wooden Universal Flat Pallet[J]. Journal of Central South University of Forestry and Technology, 2017, 37(8): 135-138.

[8] 曹菲. 木托盘受力性能理论分析及有限元模拟[J]. 包装工程, 2016, 37(23): 50-54.

CAO Fei. Theoretical Analysis and Finite Element Simulation of The Mechanical Properties of Wooden Pallets[J]. Packaging Engineering, 2016, 37(23): 50-54.

[9] 巩桂芬, 李毅, 孔腾华. OSB板托盘的叉举试验及有限元分析[J]. 包装工程, 2017, 38(19): 137-141.

GONG Gui-fen, LI Yi, KONG Teng-hua. Fork Lift Test and Finite Element Analysis of OSB Plate Pallet[J]. Packaging Engineering, 2017, 38(19): 137-141.

[10] WASEEM A, NAWAZ A, MUNIR N, et al. Comparative Analysis of Different Materials for Pallet Design using ANSYS[J]. International Journal of Mechanical & Mechatronics Engineering, 2013, 13(2): 26-32.

[11] BERNUZZI C, PIERI A, SQUADRITO V. Warping Influence on the Static Design of Unbraced Steel Storage Pallet Racks[J]. Thin-Walled Structures, 2014, 79: 71-82.

[12] GB/T 17657—2013, 人造板及饰面人造板理化性能试验方法[S].

GB/T 17657—2013, Test Method for Physical and Chemical Properties of Wood-Based Panels and Decorative Wood-Based Panels[S].

[13] GB/T 14018—2009, 木材握钉力试验方法[S]

GB/T 14018—2009, Test Method for Nail Holding Power of Wood[S].

[14] 徐秉业, 王建学. 弹性力学[M]. 北京: 清华大学出版, 2007: 133-144.

XU Bing-ye, WANG Jian-xue. Elasticity[M]. Beijing: Tsinghua University Press, 2007: 133-144.

[15] 王润富. 弹性力学问题的变分法[M]. 北京: 科学出版社, 2018: 151-169.

WANG Run-fu. Variational Method for Elasticity Problems[M]. Beijing: Science Press, 2018: 151-169.

[16] GB/T 2934—2007, 联运通用平托盘主要尺寸及公差[S].

GB/T 2934—2007, Main Dimensions and Tolerances of General Flat Pallets for Intermodal Transportation[S].

[17] 申远. 胶合板与实木材料力学性能实验研究与仿真分析[D]. 株洲: 湖南工业大学, 2019: 21-40.

SHEN Yuan. Experimental Research and Simulation Analysis of Mechanical Properties of Plywood and Solid Wood Materials[D]. Zhuzhou: Hunan University of Technology, 2019: 21-40.

[18] GB/T 4996—2014, 联运通用平托盘试验方法[S].

GB/T 4996—2014, Test Method of General Flat Pallet for Intermodal Transportation[S].

[19] 周炬, 苏金英. ANSYS Workbench 有限元分析实例详解[M]. 北京: 人民邮电出版社, 2017: 312-366.

ZHOU Ju, SU Jin-ying. ANSYS Workbench Finite Element Analysis Example Detailed Explanation[M]. Beijing: People's Posts and Telecommunications Press, 2017: 312-366.

Effects of the Number of Steel Nails on Bending Mechanical Properties of Pallets

GONG Gui-fena,b,c, LIU Sui-qianga,b,c, TIAN Yang-yanga,b,c

(a.Key Laboratory of Paper Technology and Special Paper Product Development of Shaanxi Province b.China Key Laboratory of Light Industry Paper-Based Functional Materials c.National Experimental Teaching Demonstration Center of Light Chemical Engineering, Shaanxi University of Science and Technology, Xi'an 710021, China)

The work aims to determine the number of steel nails that can meet the needs of safe use requirements of pallets. Pallet models with different numbers of steel nails were established through Iron CAD three-dimensional modeling software. Ansys Workbench software was used to perform finite element simulation analysis on a pallet with 1-5 steel nails. Then, a bending strength test of the pallet was conducted to obtain its actual deformation and compare the finite element results with the test results. Under the load of 3.5 kN, the maximum bending deformation of the pallet was continuously reduced. Finite element results: the maximum deformation of pallet with a nail tray was 48.624 mm, 2 nails was 46.139 mm, 3 nails was 38.740 mm, 4 nails was 25.280 mm, and 5 nails was 22.899 mm. Test results: the maximum deformation of pallet with 1 nail was 46.654 mm, 2 nails was 43.572 mm, 3 nails was 36.344 mm, 4 nails was 30.697 mm, and 5 nails was 27.273 mm. The test results had the same trend as the finite element results, verifying the reliability of the simulation. With the continuous increase in the number of steel nails, the bending resistance of plywood pallets is continuously enhanced. When the number of steel nails reaches 4, the safeuse requirement of the pallet can be met.

number of steel nails; pallets; bending strength; finite element analysis; bending deformation

TB485.3

A

1001-3563(2022)01-0141-07

10.19554/j.cnki.1001-3563.2022.01.018

2021-08-11

国家自然科学基金（51575327）；陕西省教育厅重点实验室及基地项目（16JS014）；陕西省教育厅2014陕西本科高校专业综合改革试点子项目（陕教高[2014]16号）

巩桂芬（1974—），女，陕西科技大学副教授，主要研究方向为缓冲包装动力学、运输包装和包装结构设计。