编码激励在岩石衰减(1/Q)检测中的应用

朱维，王尚旭*，吴何珍，翟鸿宇，和泰名，李长征

1 中国石油大学(北京)油气资源与探测国家重点实验室，北京 102249 2 中国地震局地球物理研究所，北京 100081 3 黄河水利科学研究院，郑州 450003

0 引言

岩石超声检测技术是研究地震波传播特征的重要物理模拟手段，实验室超声检测结果能够为人工地震和天然地震探测地下介质变化提供参考和理论依据，是实验地震学的重要内容.利用超声波检测岩石的声学参数，如弹性模量、声速和衰减系数等，能够获得岩石内部结构和岩石强度.

岩石声学特性的广泛深入研究开始于20世纪60年代，主要分为岩石超声波速度和衰减的测量及其应用研究.一方面，利用岩石超声波速不仅可以计算岩石的弹性参数(Winkler and Liu，1996)，还可监测岩石所受应力的变化(Gladwin，1982).另一方面，由于超声波衰减对介质物性变化的敏感性高于超声波速度，因而能更精准地反映岩石的内部结构及应力状态.然而，衰减测量十分容易受到外部因素的影响，因而一直是实验地震学研究的难点.Auberger和Rinehart(1961)利用250～1000 kHz的超声波检测了八种不同岩石的衰减系数，发现以上频段内岩石的衰减与频率并不满足线性关系.Toksöz等(1979)通过对比干燥和饱和岩石的超声波衰减说明流体会增加衰减.何国梁等(2007)利用超声波衰减系数研究了砂岩高温前后内部裂隙的发展情况，认为衰减可以用来评价岩石强度.梁利喜等(2015)通过数值实验研究了超声波衰减特性与孔洞结构的关系，发现孔洞形状、尺寸、分布和密度都对衰减有影响.然而，岩石超声波衰减的测量十分依赖于检测信号的信噪比，信噪比越高检测结果就越可靠.

通过提高信号发射功率可以增强信号能量并提高信噪比.但是，由于受到仪器参数和技术规范的限制，信号发射功率仍然有限.增加信号长度也能提高信号能量，但会降低信号的分辨率.因此，编码激励技术应用而生，它通过发射一长串调制编码信号提高平均峰值功率和增强信号能量；在接收端，它利用匹配滤波器或失配滤波器将时域上的长串信号压缩为一段窄脉冲，来达到提高接收信号信噪比的同时增加系统分辨率的目的.目前编码激励技术已被应用于医学超声成像 (O′Donnell，1992；Misaridis et al.，2000；Zhao et al.，2007；Fu et al.，2014；Zhou et al.，2014)、无损检测(Wei et al.，2010；Li et al.，2013；Arora and Mulaveesala，2017；Lasaygues et al.，2018)以及地震探测领域(Bernhardt and Peacock,1978；Chapman et al.，1981；Barbier，1982；Park et al.，1996；Wong and Stewart，2006；葛洪魁等，2006).常用编码信号可以被分为连续编码，如频率调制信号，和相位编码，如巴克序列和正交Golay互补序列等(Chiao and Hao,2003；Zhao et al.，2007；Fu et al.，2014).其中，线性调频信号(LFM)是最简单且最重要的编码，已被用来检测人体内部器官病变(O′Donnell，1992；Misaridis et al.，2000；Misaridis and Jensen，2005)、材料内部缺陷(Wei et al.，2010；周正干等，2014)以及岩石的速度(李长征等，2013).LFM信号优点突出，但对硬件要求较高，需要多级的发射器和用于匹配滤波的多级解码滤波器.二进制编码信号只需要二相脉冲发生器和解码器，因而成本更低(Zhao et al.，2007)，最近也逐渐受到人们重视(Hu et al.，2006；Leavens et al.，2009；Mulaveesala and Ghali，2011；Zhou et al.，2014；Fu et al.，2014；Lu et al.，2015；朱维和吴何珍，2017；Zhang et al.，2018；Wu et al.，2020).由于Barker编码具有完美的自相关性能，它已被用于医学高频超声成像(刘凯和高上凯，2007)、混凝土缺陷检测(李长征和王锐，2013)以及非接触超声无损检测等方面.最近，它被引入到岩石的超声波速度的精确检测中(Wu et al.，2020；李长征等，2013；朱维和吴何珍，2017).

然而，要将该项技术引入到岩石品质因子Q值检测中仍存在较大困难.朱维和吴何珍(2017)指出衰减引起的波形畸变会降低编码信号的脉冲压缩性能，可能会影响衰减的检测.因此为了获取准确的Q值，必须选择脉冲压缩性能受衰减影响更小的编码信号.为了评估衰减对编码信号脉冲压缩性能的影响，我们利用数值实验对编码激励技术进行了测试.通过使用编码激励方法的实验室实例，给出了检测岩石品质因子Q值的流程，并介绍了如何利用衰减监测三轴压缩时岩石的变形过程.

1 基本原理

1.1 衰减检测

一般来说，穿过衰减介质后，超声波的频域表达式可以写为：

W(ω)=S(ω)*Gtr(ω)*Hm(ω)+N(ω),

(1)

式中，*代表乘积，ω是角频率，S(ω)是激励信号频谱，N(ω)是噪声频谱,Gtr(ω)和Hm(ω)分别是换能器和衰减介质的传递函数：

(2)

式中，c和Q分别是衰减介质的速度和品质因子，z为超声波在介质中的传播距离.实验室中，岩石样品的衰减往往是相对于已知速度和衰减的参考样品进行测定的，这就是被人熟知的谱比法.如果选定的参考样品近似为无衰减介质(如铝样)，则两个样品的振幅谱之比可以写为：

(3)

式中，τ为透射系数，下标“r”代表参考样品，SNR是信号与噪声的振幅之比：

SNR=|W(ω)|/|N(ω)|,

(4)

如果SNR很高，即1/SNR～0，那么方程(3)可以表示为：

(5)

式中，α为衰减系数：

(6)

因此，衰减系数可以通过方程(5)的线性拟合之斜率k来确定.于是品质因子Q就可以利用方程(6)计算得到.然而，当SNR很低时噪声的影响无法被忽略，斜率k不能代表衰减系数.因此，低信噪比信号不能通过谱比法准确检测衰减.为了提高衰减检测精度，提高接收信号信噪比成为关键.本研究将编码激励方法引入到岩石衰减检测中，通过脉冲压缩来提高接收信号信噪比.

1.2 编码激励

如图1所示，编码信号s(t)激励换能器向岩石样品发射超声波，超声波在穿透岩石后在另一端被接收换能器接收并转换成电信号：

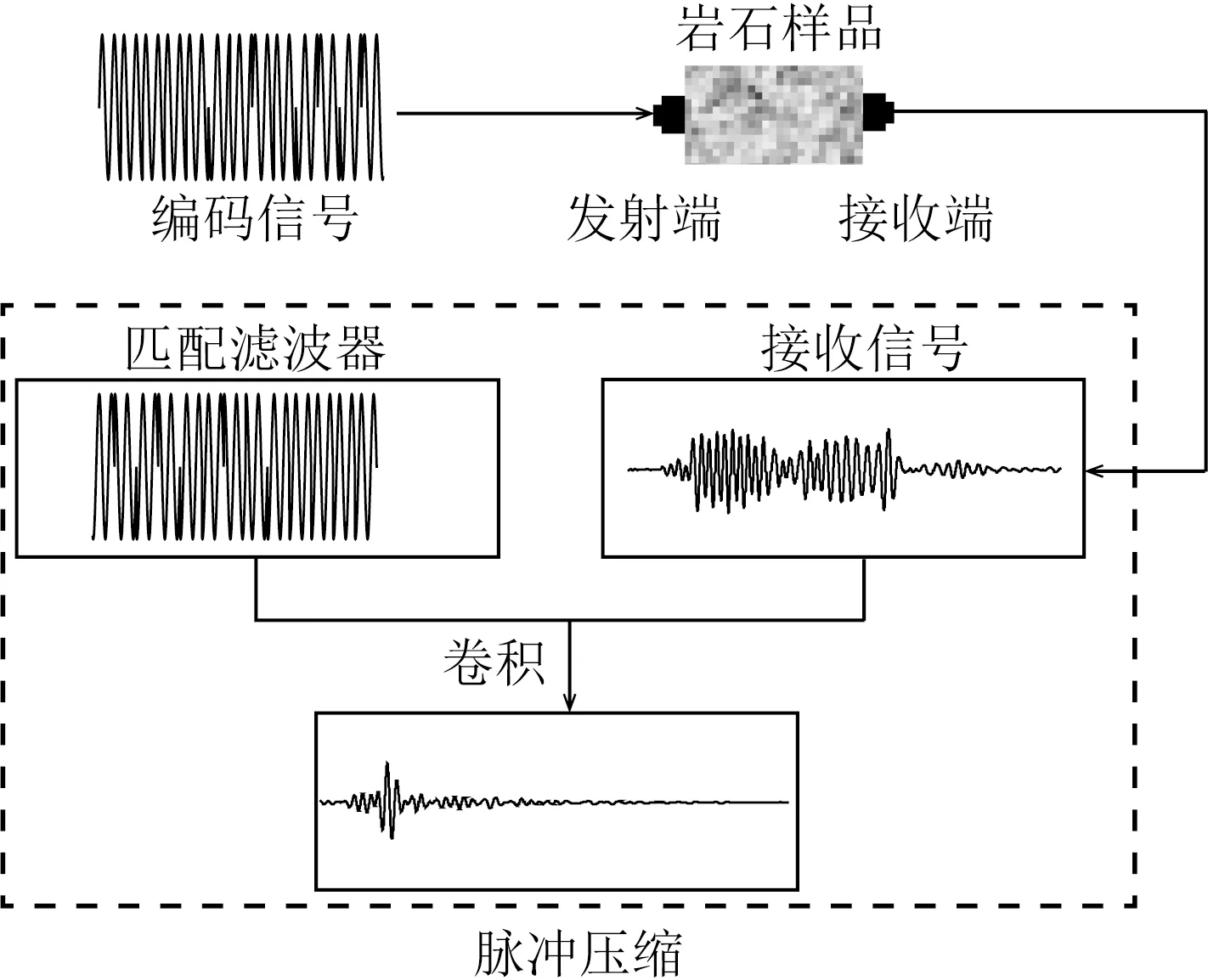
图1 编码激励超声测试系统与脉冲压缩原理Fig.1 Ultrasonic testing system for coded excitation and the principle of the pulse compression

y(t)=(s(t)⊗hTtr(t)⊗hm(t))⊗hRtr(t)+n(t),

(7)

式中，⊗表示卷积，hm(t)为岩石样品传输特性函数，n(t)为随机噪声，hTtr(t)为发射换能器响应函数，hRtr(t)为接收换能器响应函数，通常二者是相等的.在得到接收信号y(t)后，需通过匹配滤波器对其进行脉冲压缩(或称解码).设匹配滤波器为spc(t)，并令gtr=hTtr(t)⊗hRtr(t)，则脉冲压缩结果可表示为：

ypc(t)=(s(t)⊗gtr(t)⊗hm(t)+n(t))⊗spc(t)

=s(t)⊗spc(t)⊗gtr(t)⊗hm(t)+n(t)⊗spc(t),

(8)

理想情况下，

s(t)⊗spc(t)=κδ(t),

(9)

式中κ为大于1的常数，则(8)式可写为：

ypc(t)=k·gtr(t)⊗hm(t)+n(t)⊗spc(t),

(10)

式中n(t)⊗spc(t)即噪声与接收信号的互相关.由于它们是不相关的，因此经过脉冲压缩后噪声得到了明显的抑制.

常用的编码信号主要可以分为频率编码和相位编码.每个编码信号会使用不同的调制函数.对于线性调频信号(LFM)，其调制函数可以写为：

s(t)=sin(2π(f0-B/2)t+πμt2)，0≤t≤T

(11)

式中f0是换能器的中心频率，B是LFM的带宽，μ=B/T是扫频速率，T是LFM的持续时间.图2a展示了LFM信号的波形.对于相位编码，其调制函数由(12)式给定:

(12)

式中，p(t)是决定了相位编码信号的频谱的载频函数，c是长度为N的编码，Tp是每片编码的持续时间.图2e展示了正弦载频调制的巴克编码信号(BS).

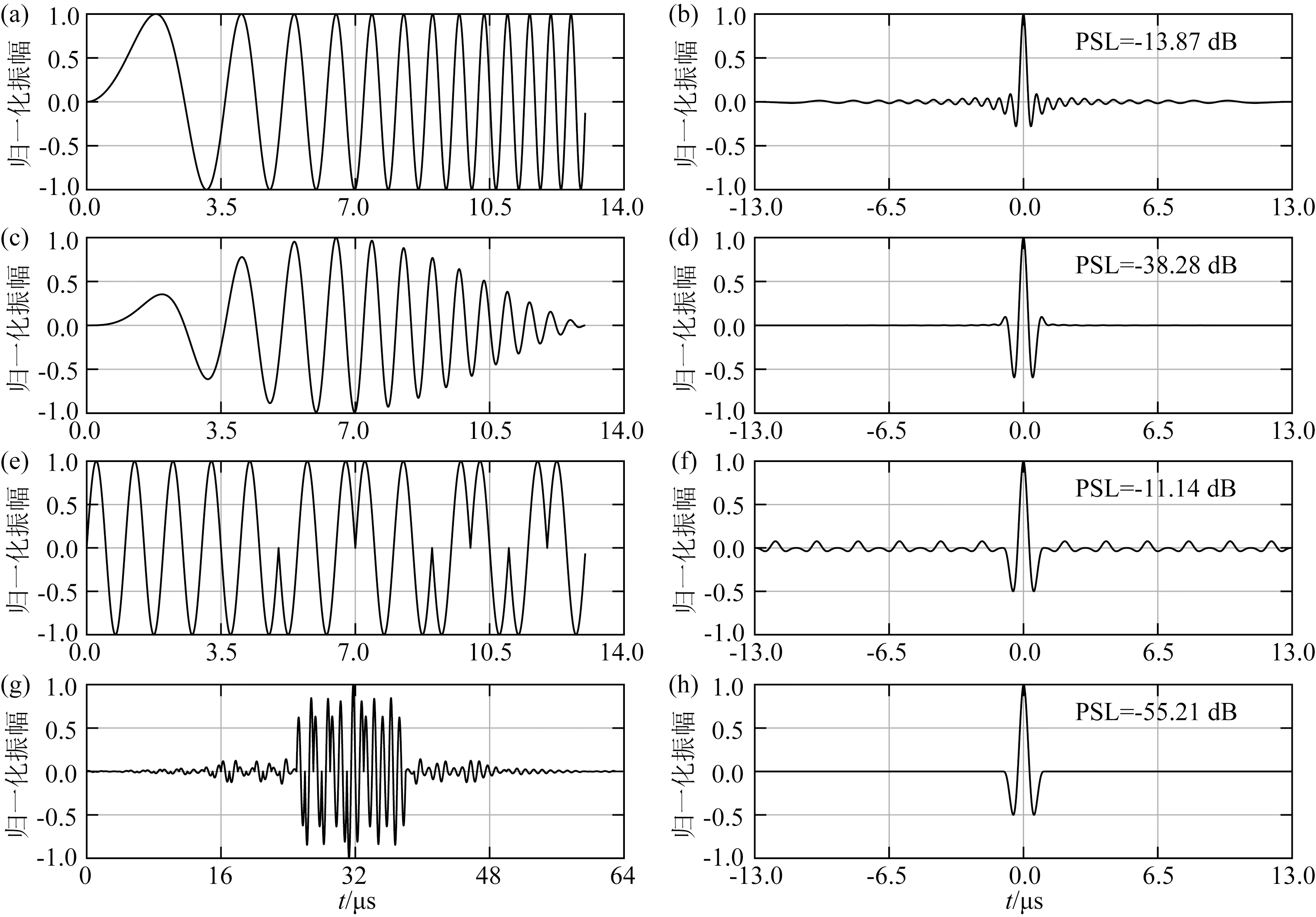
图2 编码信号及相应脉冲压缩信号(a)LFM信号；(b)匹配滤波后(a)的脉冲压缩信号；(c)幅度削减的LFM信号；(d)匹配滤波后(c)的脉冲压缩信号；(e)BS信号；(f)传统匹配滤波后(e)的脉冲压缩信号；(g)BS信号的逆滤波器；(h)利用逆滤波器匹配滤波后(e)的脉冲压缩信号.Fig.2 Coded signals and their corresponding pulse compressed signals(a)LFM signal;(b)Pulse compressed signal of (a)after matched filtered;(c)Tapered LFM signal;(d)Pulse compressed signal of (c)after matched filtered;(e)BS signal;(f)Pulse compressed signal of (e)after traditionally matched filtered;and (g)Inverse filter of BS;(h)Pulse compressed signal of (e)after matched filtered by inverse filter.

然而，不同编码信号的脉冲压缩性能是不同的，通常可以由信噪比增益(GSNR)、距离旁瓣水平(RSL)以及主瓣宽度(MLW)进行评价.信噪比增益通常是指信号匹配滤波前后信噪比的增加值，理论上GSNR由编码信号的时间带宽积(TBP)决定：

GSNR=10log10(TBP)(dB).

(13)

一般而言，编码信号通过匹配滤波后，在主瓣附近还会出现比较明显的旁瓣，为了衡量主瓣与旁瓣的相对大小可以用峰值旁瓣水平(PSL)进行评价.PSL越低说明编码信号的脉冲压缩性能越好.

(14)

但是旁瓣往往是无法避免的，一般采用数学方法抑制这些旁瓣对速度或Q值检测的影响.对频率编码信号(如LFM信号)，需要采用诸如振幅削减技术的方法对发射源进行处理，从而达到抑制旁瓣的目的，但会损失一定的轴向分辨率.根据图2b可以看到其脉冲压缩波形存在严重旁瓣.图2c为振幅削减后的线性调频信号(TLFM)，从图2d可以看到其脉冲压缩波形旁瓣得到了明显抑制.对于相位编码信号(如Barker编码)，可以通过设计新的匹配滤波器(如伪逆滤波器)抑制旁瓣；图2f展示了BS信号通过传统匹配滤波后的脉冲压缩波形，而图2h则展示了利用伪逆滤波器滤波后的脉冲压缩波形，可以看到旁瓣得到了明显抑制.最后一个评价指标——主瓣宽度一般是指编码信号自相关函数主瓣的宽度，它是衡量信号轴向分辨率的重要指标，主瓣宽度越窄说明系统的分辨率越高，因此编码信号经过脉冲压缩后必须具有较窄主瓣宽度.

选择合适的编码信号以后，我们就可以进行衰减检测了.利用编码信号检测超声波衰减的基本流程如图3所示.

图3 利用编码激励技术检测岩石衰减的流程图Fig.3 Flow chart of the measurement of the attenuation in rock using coded excitation technique

2 数值实验

由于衰减会严重影响编码信号的脉冲压缩性能，对不同编码信号检测衰减的能力评估是十分必要的.我们选择正弦信号(Sine)、BS信号以及TLFM信号作为激励信号生成了40组接收波形，其Q值范围为5～200，合成信号都加入了相同功率的噪声.图4展示了Q=5时利用不同激发源生成的接收波形及相应的脉冲压缩波形.从图中可以看到，脉冲压缩后噪声被明显抑制.

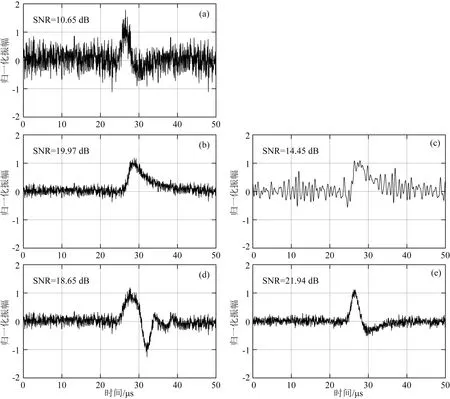
图4 Q=5时，不同激励源激发得到的理论接收信号及脉冲压缩信号(a)、(b)和(d)分别是Sine信号、TLFM和BS信号作为激励源的接收信号；(c)和(e)分别是匹配滤波后(b)的脉冲压缩信号和利用逆滤波器匹配滤波后(d)的脉冲压缩信号.Fig.4 The synthetic received signals and pulse compressed signals obtained by different excitation sources when Q=5Received signals excited with (a)Sine signal,(b)TLFM signal and (d)BS signal;(c)Pulse compressed signal of (b)after matched filtered;(e)Pulse compressed signal of (d)after matched filtered by inverse filter.

图5是衰减对编码信号脉冲压缩性能影响的评估结果.可以看到，衰减会严重影响编码信号的脉冲压缩性能.一方面，TLFM信号的GSNR会随衰减的增大而减小，而BS信号却并不受衰减的影响.由于不同频率的能量衰减不同，高频信息容易缺少或丢失，从而导致接收信号的中心频率向低频偏移，因而导致频率编码接收波形畸变十分严重；而相位编码信号的频率信息包含在载波信号中，因此相位编码激励源接收信号失配较小.另一方面，当Q值>5时，BS信号的GSNR和MLW都大于TLFM信号；当Q=5时，则正好相反.然而，由于TLFM信号的信噪比增益明显低于BS信号，利用编码信号求取Q值时，TLFM信号不如BS信号适合Q值的检测.

为了进一步检测编码信号对衰减的检测能力，我们对这些波形采用谱比法求取了Q值，如图5d所示.根据计算结果，BS与TLFM激励源检测的Q值误差都低于正弦激励源的结果，这表明编码激励源能够提高Q值的检测精度.同时，从图5d可以看到，Q<20时，TLFM激励源计算的Q值误差大于BS激励源.这是因为衰减较大时，TLFM信号的脉冲压缩性能受衰减影响较大，接收波形失配严重，从而导致了更大的Q值的计算误差，因此TLFM信号并不适合应用于较大衰减介质的Q值检测.当Q>20时，TLFM激励源计算的Q值误差小于BS激励源，这是因为TLFM激励源的接收信号经过脉冲压缩后保存了更多高频能量的缘故.综合以上结果可知，编码激励源能提高Q值的检测精度；对于衰减较大的介质，BS编码激励源检测的Q值更准确，而对衰减较小的介质，TLFM激励源检测的Q值更准确.

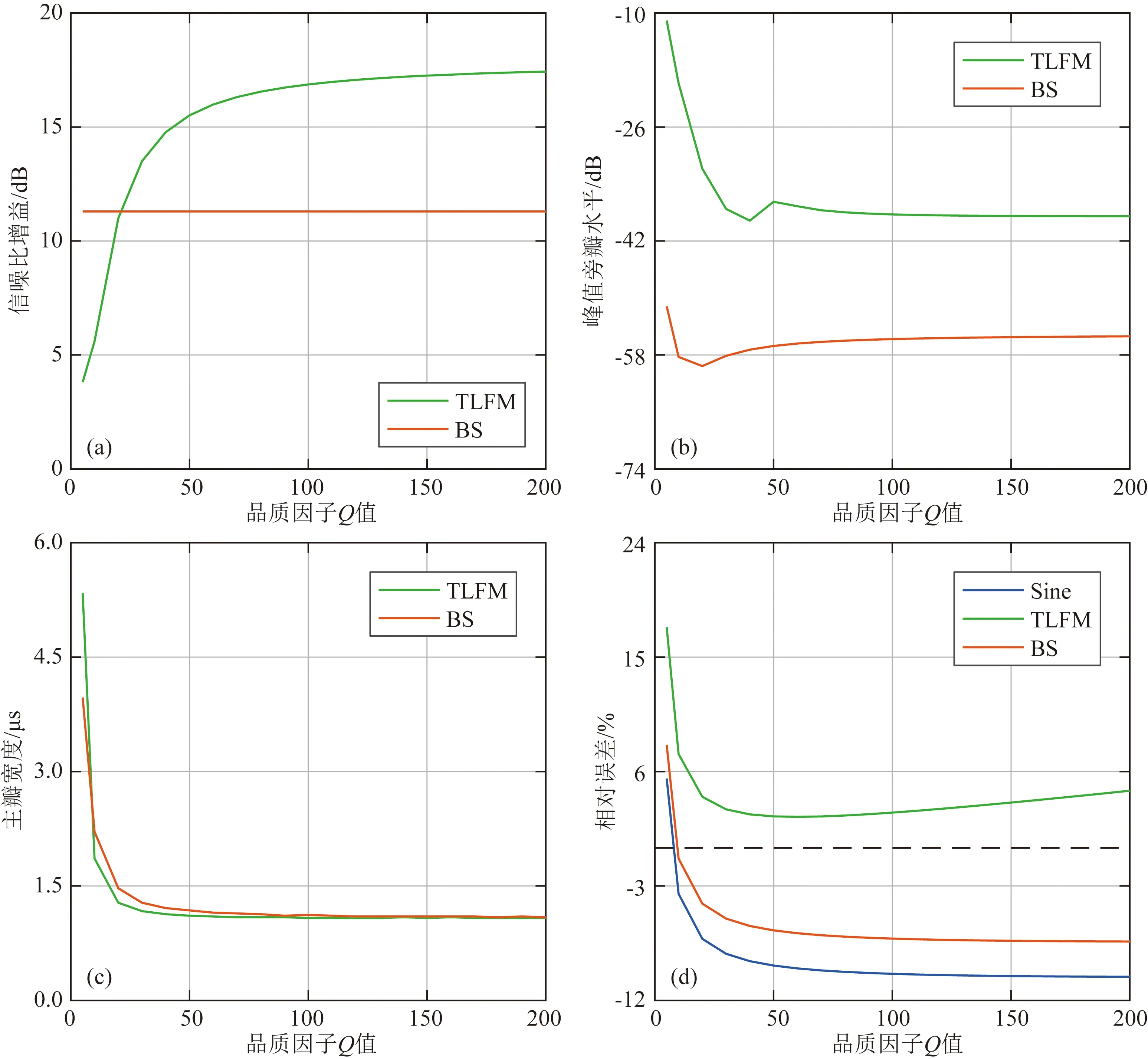
图5 利用TLFM和BS激励源合成的接收波形计算得到的脉冲压缩波形的(a)信噪比增益，(b)峰值旁瓣水平，(c)主瓣宽度以及(d)Q值检测相对误差随品质因子的变化Fig.5 (a)The gain in SNR (GSNR),(b)peak sidelobes level (PSL)and (c)main-lobe width (MLW)of the waveforms compressed from the synthetic signals excited by TLFM and BS,and (d)the relative errors of Q varied with quality factor

3 实际应用

我们利用编码激励技术测试了不同样品的Q 值并监测了岩石三轴加载过程时的衰减变化.

3.1 测试1：岩石Q值检测

本测试采用中心频率为1 MHz的超声波换能器测试了有机玻璃、人工砂岩(环砂比为3∶8)及天然砂岩(采自重庆武隆)的Q值(图6).利用单脉冲信号(这里采用Sine信号)和编码信号检测的Q值列于表1中.表中还列出了利用标准测试方法获得的Q值.从表中可以看到对于有机玻璃，TLFM编码激励源检测的Q值最接近参考值，而对于人工砂岩和天然砂岩BS激励源检测的Q值最接近参考值.这与数值实验的结论是一致的.

3.2 测试2：岩石破裂过程中的衰减监测

岩石破裂过程中内部会经历旧微裂纹闭合、新微裂纹产生、集结并最终发生宏观破裂等过程.由于岩石微结构的变化会引起岩石衰减的变化，因此通过监测衰减就能反映岩石受压过程中内部微结构的变化.本测试对测试1中天然砂岩开展了三轴压缩实验.加载设备为SANS电液伺服压力机，其最大载荷为300 kN.岩石样品置于围压容器中保持5 MPa围压不变，轴压采用应力控制模式(加载速率300 N·s-1).轴向位移随应力的变化如图7中黑线所示.为了监测岩石变形过程中超声波衰减的变化，我们将换能器置于岩石样品上下两端用于发射和接收超声波形.整个加载过程共记录23组不同激励源的检测波形.利用这些波形我们计算了不同加载阶段岩石的衰减(图7).

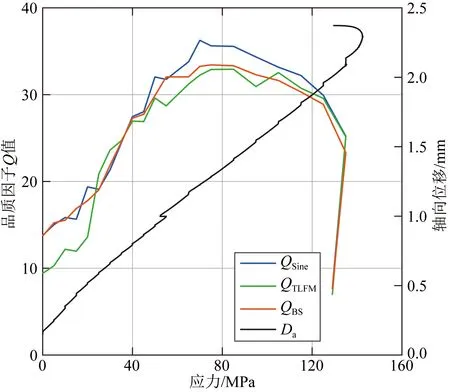
图7 品质因子Q值及轴向位移随应力的变化QSine，QBS和QTLFM分别代表Sine信号、BS信号和TLFM信号激励源检测波形得到的Q值；Da代表轴向位移.Fig.7 Quality factor Q and axial displacement varied with the stressQSine,QBS and QTLFM represent the quality factor measured with the signals excited by Sine,BS and TLFM,respectively.Da represents the axial displacement.

根据前人研究，岩石变形过程中，衰减会经历先变小达到一定值后保持稳定最后由于新裂纹的产生又逐渐减小的过程(Lockner et al.，1977).从图7中衰减随应力的变化曲线来看，三种信号都能很好地反映这一规律.这说明编码信号可以用于监测受载岩石的变形和破裂过程.同时，实验结果表明应力小于25 MPa时，岩石的Q值小于20且TLFM激励源检测的Q值明显小于单脉冲和BS激励源的检测结果.这再次验证了数值实验得出的结论——衰减较大时TLFM激励源的检测结果误差更大.由于岩石受压变形过程中Q值变化较大，要在整个过程中都获得更小误差的Q值，这就要求编码信号具有更稳定的脉冲压缩性能.因此Barker编码信号比TLFM信号更适合监测岩石的变形过程.

4 结论

利用编码激励技术检测岩石的Q值是可行的，结果是可靠的.通过对编码激励与脉冲压缩的基本原理、方法、实验和应用的系统分析，得出编码激励技术可以通过脉冲压缩提高信噪比，但是岩石的衰减会削弱编码信号的脉冲压缩性能的结论.虽然幅度削减的线性调频信号的脉冲压缩性能比正弦调制的Barker编码更好，但是当Q值小于20时即岩石衰减较大时，TLFM的信噪比增益下降更为严重，TLFM激励源检测的Q值误差更大.我们利用正弦信号，正弦调制的Barker编码信号和幅度削减的线性调频信号测量了有机玻璃、人工砂岩以及天然砂岩Q值.实验结果表明编码激励技术能够通过脉冲压缩来抑制噪声，提高Q值检测精度.另外，我们还利用编码激励源检测了砂岩在三轴压缩过程中Q值的变化并监测了岩石的变形和破裂过程.实验结果表明，与TLFM激励源相比BS激励源在衰减较大时检测的Q值误差更小，因而更适合监测衰减不断变化的受压岩石的变形过程.

尽管我们已经论证了编码激励在超声频段测试岩石Q值时的可靠性与适用性，但是当岩石中黏土矿物含量较高或包含流体时，岩石的弹性波速度和Q值都可能出现频散效应.当然，对于超声频段的弹性波而言，这种频散可能只有在岩石衰减很强时才会显著.但是，由于频散效应的存在，要将编码激励在超声频段的应用推广至地震频段仍需进一步的研究.