吊舱式高温超导全张量磁梯度测量系统研发与应用研究

郭华,王明,岳良广,常畅,王铭超,姚雨暘,管琳琳,郭建燕

1 中国自然资源航空物探遥感中心，北京 100083 2 吉林大学，长春 130026 3 中国地质大学(北京)，北京 100084 4 中国地质科学院地质研究所，北京 100037

0 引言

随着高精度超导量子干涉磁强计(SQUID)的快速发展，以及磁场张量测量技术的独特优势(Nabighian et al.,2005)，全张量磁梯度测量成为国内外磁法勘探技术领域的热点(张昌达,2006;任胜男,2010)，借此，航空磁测由总磁场强度测量和三分量测量，发展到了全张量磁力梯度测量(Bruce and Justin,2003;郑婷,2015；潘琦等，2018；郑强等，2019).全张量磁力梯度测量主要有高温超导和低温超导航磁全张量梯度测量系统，由于液氮具有方便携带以及价格低廉的优势，因此高温超导航磁全张量梯度测量系统必将是仪器设备研制的方向，但是高温超导SQUID的研制难度更大.目前，德国、美国、澳大利亚、加拿大以及中国先后开展了基于SQUID的航磁超导全张量梯度测量系统的研制工作，并在低温超导SQUID芯片研制方面取得了一定了成就(Koch et al.,1996;Schmidt et al.,2004;Bracken and Brown,2005;Stolz et al.,2006;Gamey,2008;Chwala et al.,2012;唐雨和杨会永,2012;Sui et al.,2014;王一,2015;杜昱辰,2019；申茂冬等，2016).虽然我国在磁梯度张量探测方面研究起步较晚，与国际先进水平仍存在较大差距，但也在逐步的展开对于全张量磁梯度测量设备的研究与设计.国内仅中国自然资源航空物探遥感中心与吉林大学等多家科研院所组建的一支科研团队在开展航磁高温超导全张量梯度测量系统的研究工作；而其他其他单位在研制的是低温超导航磁全张量梯度测量系统，其中中国科学院上海微系统与信息研究所依托国家重大科研装备研制项目“深部资源探测核心装备研发”项目研制出了航空低温超导全张量磁梯度测量系统，并在内蒙古某区域开展了航空超导全张量磁梯度测量试验飞行，成功获取全张量磁梯度分布图并实现了对模拟磁异常体的定位.

航磁全张量梯度测量技术主要测量磁矢量的三个分量在地理坐标系三个方向上的空间变化率，其探测效率高，运行成本低，受地磁场的影响较小，反映的磁场信息丰富，应用领域广泛，对促进我国经济发展与保障国家资源安全方面具有重大意义，对其测量技术与仪器研发工作也已经迫在眉睫.中国自然资源航空物探遥感中心在“十三五”国家重点研发项目“航空磁场测量技术系统研制”支持下，与吉林大学等多家科研院所合作开展了航磁高温超导全张量梯度测量系统的研究工作，研发了适用于直升机挂载的吊舱式高温超导全张量磁梯度测量仪工程样机，并针对其应用于航空全张量磁梯度测量进行可行性研究，在江苏省丹阳市试验区开展了飞行试验，成功地获取了试验区全张量磁梯度分布图，测试结果表明吊舱式高温超导全张量磁梯度测量仪各项指标满足航磁测量技术规范的要求，测量精度优于±30 pT·m-1，为打破国外技术垄断、自主设计出国产化的航空超导全张量磁梯度测量系统奠定基础.

1 测量方法原理

航空全张量磁梯度测量技术是测量地磁矢量的三个分量(Bx、By、Bz)在空间中x、y、z三个方向上的梯度，共9个要素，其矩阵可表示为：

(1)

根据麦克斯韦方程，无源空间地磁矢量场的旋度与散度均为0，即divB=0，rotB=0，可得公式(1)中的9个分量里有5个是独立分量(杜昱辰,2019)，因此，公式(1)简化为:

(2)

利用公式(2)即可获取磁场的9个一阶梯度张量信息，即全张量磁梯度测量的测量对象(申茂冬等，2016).

在航空高温超导全张量磁梯度测量系统中，8个高温DC-SQUID传感器通过一定的空间位置安装，组成全张量磁梯度探头(图1).在探头坐标系o-xyz中，X轴和Y轴分别布置3个DC-SQUID传感器，Z轴方向布置两个DC-SQUID传感器；因此对于某一方向上的磁场变化和空间距离都已知，可以计算出相应的全张量中的某一要素；8个高温DC-SQUID传感器按照图中的方式安装可以测得全张量9个全要素中的5个独立分量，进而可以求得全张量的9个全要素.

图1 高温超导全张量磁梯度探头结构示意图Fig.1 Schematic diagram showing structure of high-temperature superconducting full-tensor magnetic gradient probe

2 测量系统结构

图2所示为航空高温超导全张量磁梯度仪系统构成示意图，主要由SQUID构成的全张量磁梯度探头、无磁杜瓦、多通道数控SQUID读出电路模块、数据采集系统、惯性导航系统、无磁吊舱及电源等部分构成.

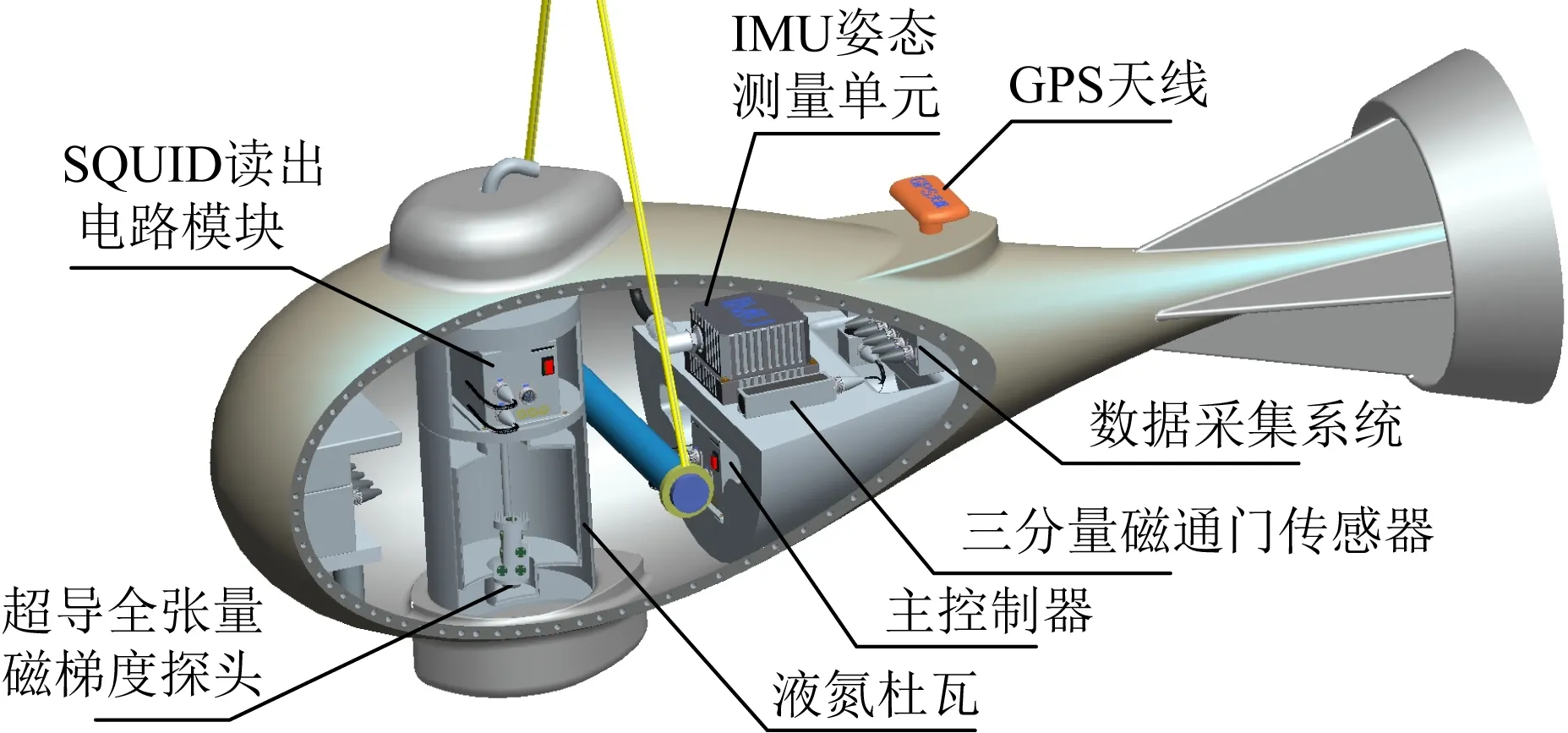
图2 高温超导全张量磁梯度仪工程样机结构组成Fig.2 Structure of high-temperature superconducting full-tensor magnetic gradient instrument

2.1 SQUID传感器

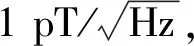
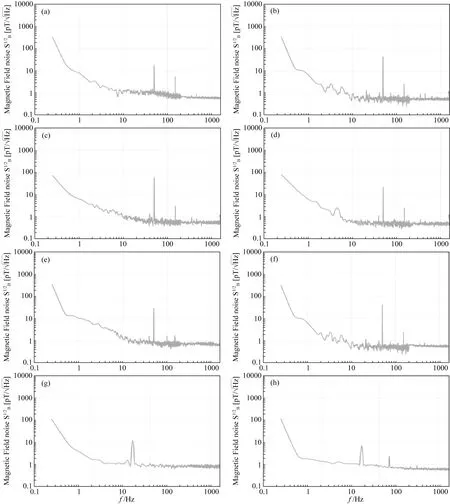
图3 选用的8个传感器噪声灵敏度测试结果Fig.3 Noise sensitivity test results of eight selected sensors

2.2 磁梯度探头结构设计

根据高温DC-SQUID器件的结构和尺寸，设计了如图4所示的高温超导全张量探头结构.探头加工材料选择绝缘电阻高、抗冲击强度和抗弯曲强度大、耐低温的FR4等级的环氧树脂材料，探头的支架顶部采用4层环氧树脂板-铝箔膜-泡沫板-铝箔膜-环氧树脂板间隔安装的方式，可以最大限度保温和隔绝热辐射与防止电磁屏蔽干扰.支架与探头之间通过细长的环氧树脂杆连接，一方面可以将探头尽可能的放置于杜瓦桶的底部，在液氮量一定的前提下尽可能的增加了SQUID传感器的工作时间，同时细长杆的质量相对较小，在环氧树脂材料比热容一定的情况下，减少了探头以及支架放置到杜瓦桶中液氮的挥发量，也起到了延长系统工作时间的作用.采用三根细长杆可以达到三角形稳定的作用，减少了探头在飞机飞行过程中发生的震动从而对磁测数据造成的干扰.探头支架的顶部设计有螺丝孔，用来与杜瓦桶进行紧固连接，同时设计有出气孔，从而确保内部气压与外部气压一致，避免吊舱发生倾斜以及其他原因导致的液氮迅速气化带来的爆炸等风险.

图4 全张量磁梯度探头结构与支架示意图Fig.4 Schematic diagram of full-tensor magnetic gradient probe structure and bracket

2.3 惯性导航系统设计

航空高温超导全张量磁梯度测量系统在进行飞行作业时，需要记录系统的姿态信息，从而完成梯度仪的姿态校正，完成梯度仪坐标系数据到地理坐标系数据的转换，同时还需要记录系统的高度信息完成面积性定高飞行以及地理位置信息，从而确定数据反演所对应的实际地理位置，指导后续进一步的资源开发和利用.

本测量系统采用的惯性导航系统为SPAN-IGM-S1型小型化高精度MEMS组合导航系统(图5)，由挪威Sensonor的高精度惯性测量单元STIM300和NovAtel OEM615板卡构成，采用一体化封装，在不需要外接传感器的前提下，能够提供125Hz的高精度3D位置、姿态和速度信息，满足航空高温超导全张量磁梯度仪的系统特点和对精度、尺寸、重量等参数的要求.

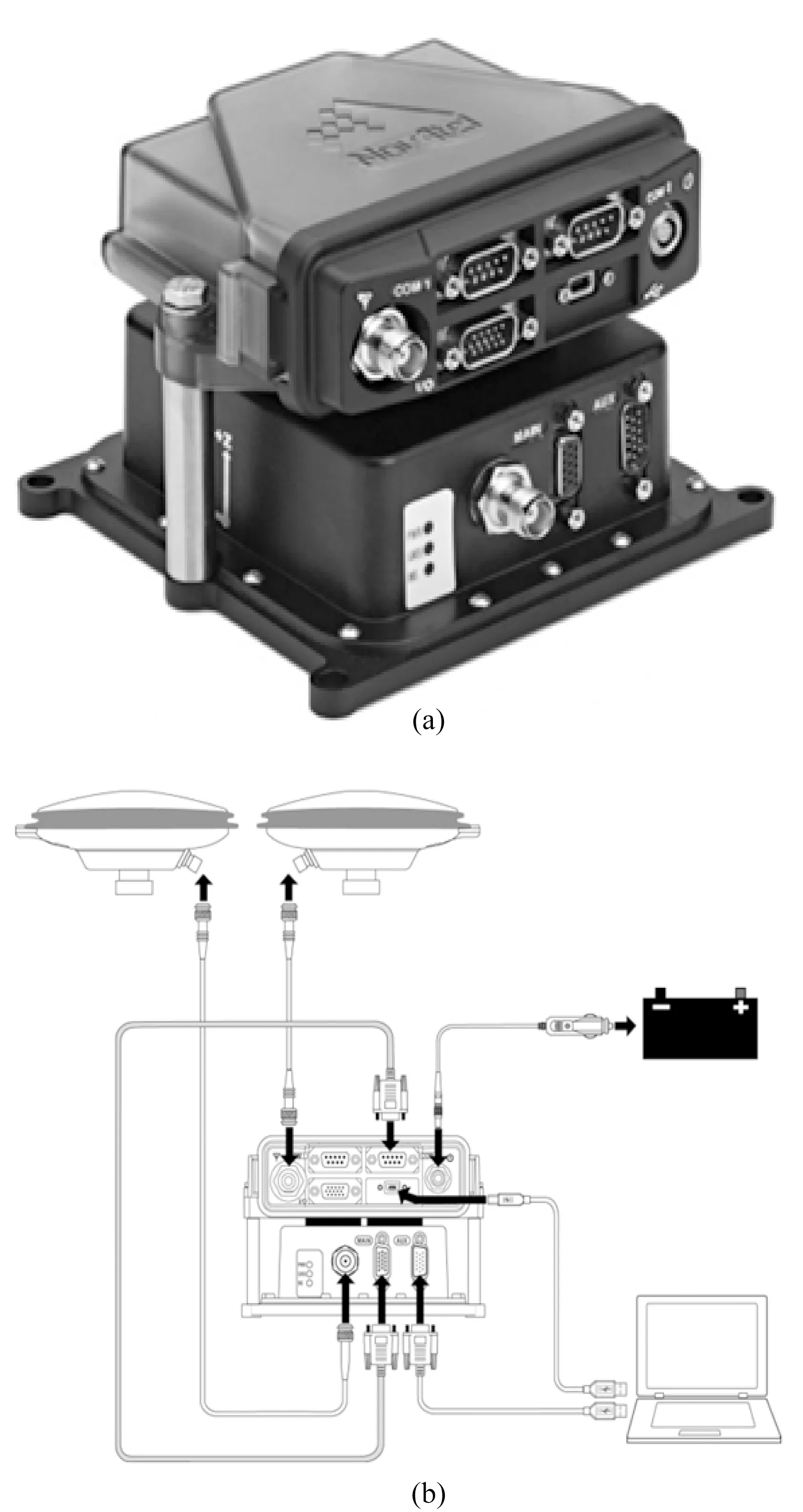
图5 惯导系统系统及接线方式示意图Fig.5 Schematic diagram showing inertial navigation system and wiring way

2.4 吊舱机械结构设计

设计了适用于直升机挂载的高温超导全张量磁梯度仪吊舱(图6)，主要采用玻璃钢纤维强化塑料材料作为吊舱的舱体，既能保证整个舱体满足飞行挂载强度要求，也满足直升机悬挂舱体的重量要求.舱体主要由主壳体、承载支架和平衡尾翼3部分组成，舱体的外形经过了空气动力学设计，可以保证直升机挂载梯度仪系统进行飞行测量作业时减少舱体的摆动，从而减少因姿态变化从而对磁传感器测量造成的影响.吊舱的舱体内部按照设计功能区通过玻璃钢隔板进行了划分，分为电源安装区、惯导安装区、NI数据采集系统安装区以及杜瓦安装区.

图6 吊舱示意图Fig.6 Photo showing pod

3 误差分析与校正

3.1 探头误差校正

SQUID传感器探头由于受到制造、加工等工艺的限制以及SQUID读出电路的影响，8个SQUID传感器很难确保传感器在三个轴向上完全相互正交，会产生三轴非正交误差，需要对此进行非正交误差校正.

非正交误差模型如图7所示，o-xyz为理想情况下的三轴磁传感器坐标系，o′-x′y′z′为非正交的三轴磁传感器坐标系.假定z轴在xoz面与z′轴重合，且yoz面与y′o′z′面重合；φ为x′轴与其在xoy面的投影之间的夹角，φ为x′轴xoy面的投影与x轴之间的夹角，ψ为y轴与y′轴之间的夹角.仅考虑非正交误差时，可用公式(3)表示三轴磁传感器的测量误差模型(高全明，2020)：

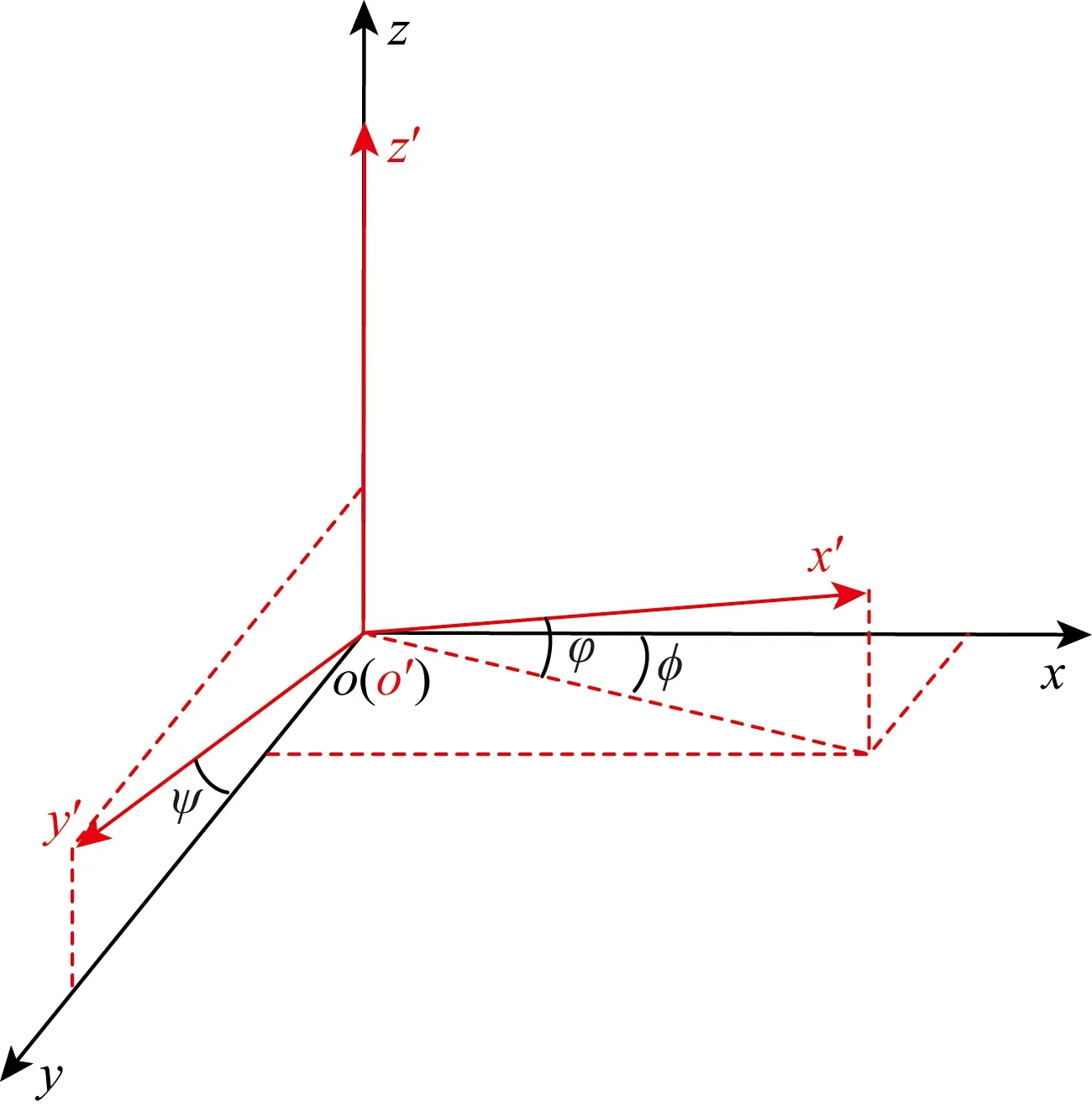
图7 非正交误差模型Fig.7 Non-orthogonal error model

(3)

其中，hm为三轴磁传感器的测量值，he为真实磁异常在完全正交方向的分量值，knor为非正交误差矩阵.

又由于SQUID传感器以及读出电路在进行电压/磁场转换系数标定时，存在一定的比例系数误差，该误差的模型可以表示为：

(4)

其中，ksf为比例系数误差矩阵.

在理想情况下，SQUID读出电路从调试状态转换为锁定状态时读出电路的值应为零.但是读出电路的输出此时会发生漂移，导致输出不为零，在较短的时间范围内，可将此偏移量作为常数计算.在只考虑零位偏移误差的情况下，误差模型可表示为：

(5)

其中，hb为零位偏移误差矩阵.

综上所述，三轴SQUID传感器测量综合误差数学模型可表示为：

hm=ksfknorhe+hb，

(6)

进而，可以得到误差综合校正模型：

he=k-1(hm-hb)，

(7)

其中，k=ksfknor.

最后利用椭球拟合的方法对误差模型的参数进行求解.基于椭球假设校正方法的基本思想：根据建立的三轴传感器误差综合校正模型与磁测轨迹椭球体拟合方程之间的关系式，求取修正关系，进而计算三轴磁传感器误差校正参数(高全明，2020).

3.2 系统姿态校正

高温超导全张量系统在进行飞机挂载飞行时，系统在空中的姿态会时刻在变化，因此需要利用惯导系统对高温超导全张量系统的飞行姿态进行记录，然后将传感器的实测数据进行姿态校正，转换到地理坐标系下.

空间中一个坐标系绕自身坐标轴旋转三次，可与另一坐标系重合，其旋转角度被称为欧拉角.因此，两个坐标系可通过欧拉角描述其转换关系，此方法称为欧拉旋转法(高全明，2020).

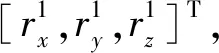
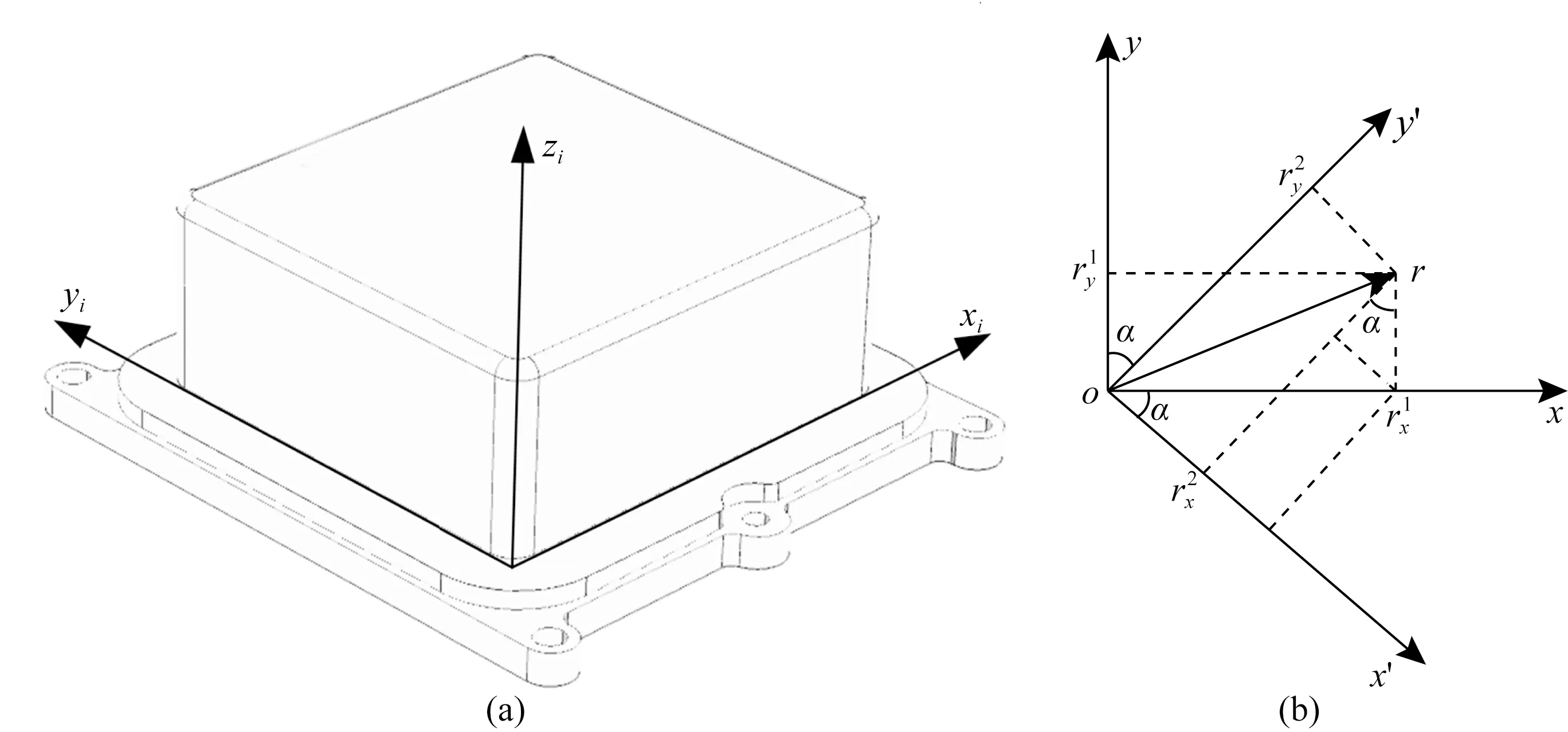
图8 惯导坐标系与姿态校正示意图Fig.8 Schematic diagram of inertial navigation coordinate system and attitude correction

(8)

式(8)可表示为矩阵形式：

(9)

因此，坐标系绕z轴旋转α角转换矩阵为：

(10)

同理可得出坐标系绕x轴、y轴旋转β角、γ角转换矩阵表达式.

高温超导全张量系统可以利用惯导系统记录的航向角、横滚角、俯仰角的变化角度数据，将SQUID传感器记录的数据统一转换到地理坐标系下，从而完成系统的姿态校正.

3.3 磁补偿飞行

磁补偿飞行的目的是消除恒定磁场、感应磁场和涡流场的干扰，对飞机姿态的影响进行校正.补偿飞行通常安排在一个地磁场平静区域，高温超导系统补偿飞行的航迹如图9所示为正方形闭合框.

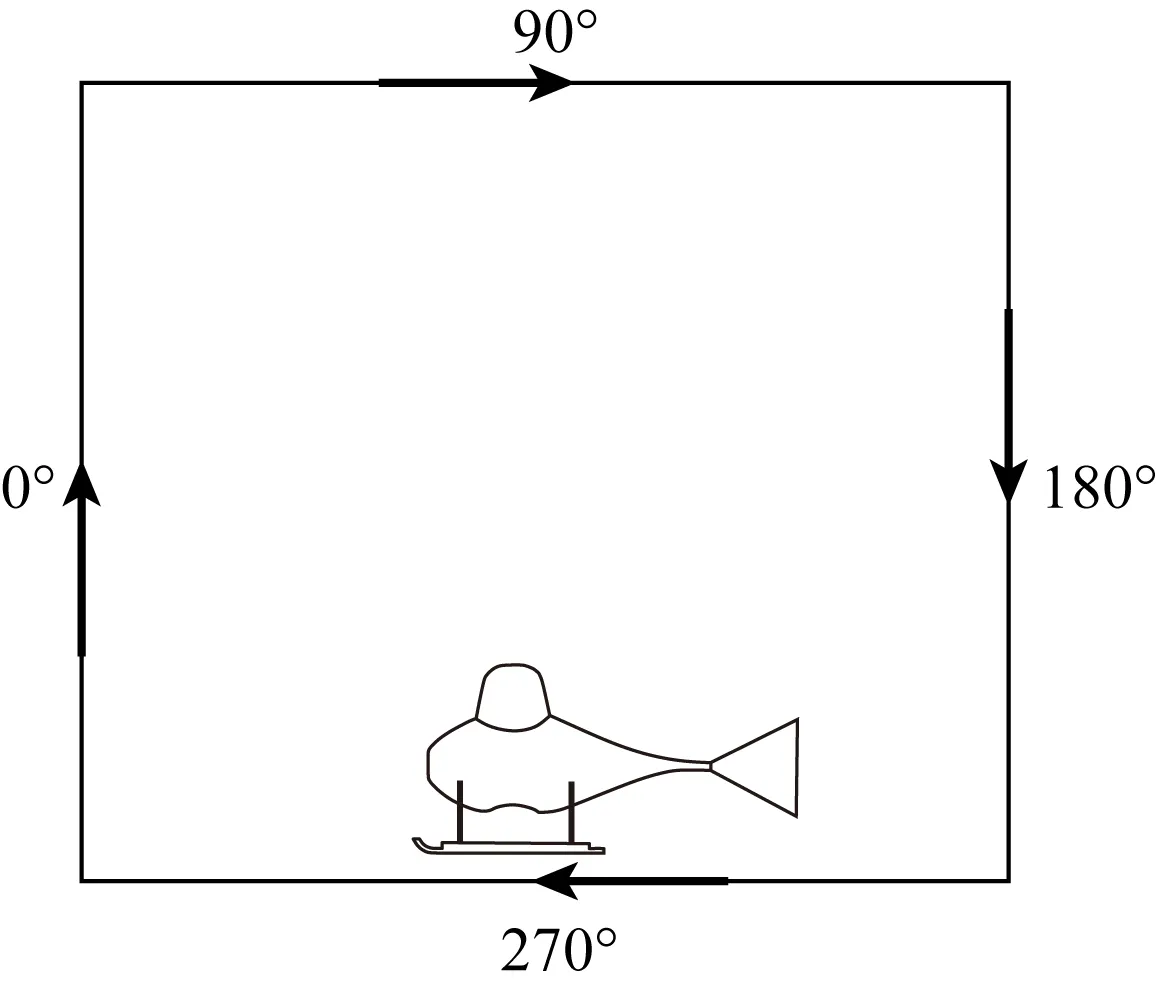
图9 磁补偿飞行航迹示意图Fig.9 Schematic diagram of magnetically compensated flight path

当飞行高度足够高时，此时假定探头测得的磁场与地下局部异常无关.飞行飞机依次沿四个边飞行，从而获取飞机飞行的姿态信息与测区的磁异常信息，进而计算得到补偿系数.在测线飞行过程中，姿态探测仪根据飞机姿态的变化计算出磁干扰值，在实测磁场中剔除磁干扰值后，即可获得补偿后的磁场值(安战锋等，2016).

对于补偿效果评价(王林飞等，2013)，《航空磁测技术规范》(DZ/T 0142-2010)(中华人民共和国国土资源部,2010)中补偿前后的标准差评价指标为：

补偿前标准差：

(11)

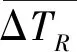
补偿后标准差：

(12)

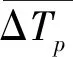
4 实际飞行试验

为了进一步验证高温超导全张量系统在实际生产中的稳定性，我们在江苏省丹阳市选择试验区进行面积性试验飞行.为了检验测量系统的噪声水平对异常的分辨能力，我们在试验区选择磁场相对平稳变化，但又包含局部异常点的区域进行试验飞行.

4.1 地面静态测试

为了测量高温超导全张量系统的地面静态指标，在试验区进行2.5 h静态测试，测量结果如表1和图10所示.

图10 高温超导全张量测量系统静态测试结果图Fig.10 Static test results of high-temperature superconducting full-tensor measuring system

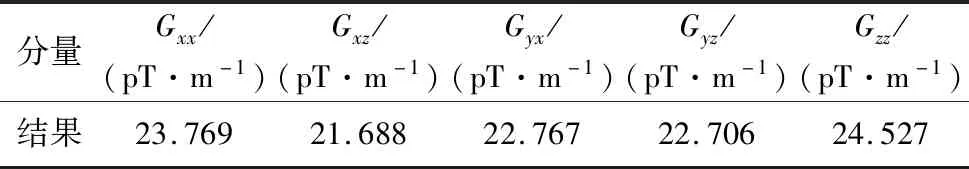
表1 地面静态测量精度四阶差分结果Table 1 Fourth-order difference results of ground static measurement accuracy

静态噪声水平计算表达式为：

(13)

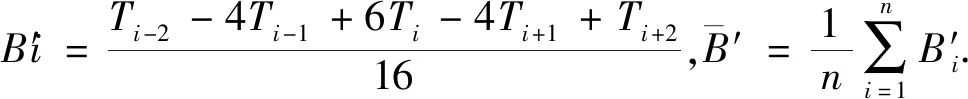
根据航磁规范里的四阶差分原理，测试结果表明，我们研制的高温超导全张量磁梯度测量仪地面静态测量精度优于±30 pT·m-1.

4.2 动态飞行测试

高温超导全张量系统直升机挂载飞行试验进行面积性飞行测线共计1013.9 km，飞行高度为200 m，共计40条测线，并通过飞行重复测线的方式验证了系统的稳定性.为了获得每条测线的动态精度指标，每条测线采集的数据按照如下的四阶差分公式计算：

(14)

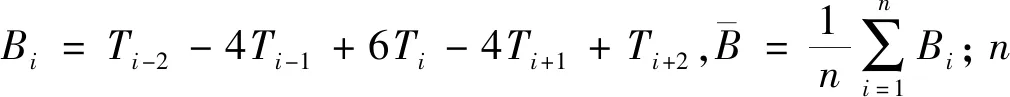
200 m飞行高度计算结果如表2所示，按照航磁规范里的四阶差分理论，其各分量动态测量平均精度要优于±30 pT·m-1.

表2 200 m高度动态飞行测量精度四阶差分结果Table 2 Fourth-order difference results of flight measurement accuracy at 200 m altitude

如图11所示为高温超导全张量200 m高度测量结果.从40条测线获得的数据结果绘制的实际面积90 km2的全张量磁梯度5个独立分量的结果图中可以看出，每个分量的效果图总体分布规律一致，磁异常点的分布较为一致.

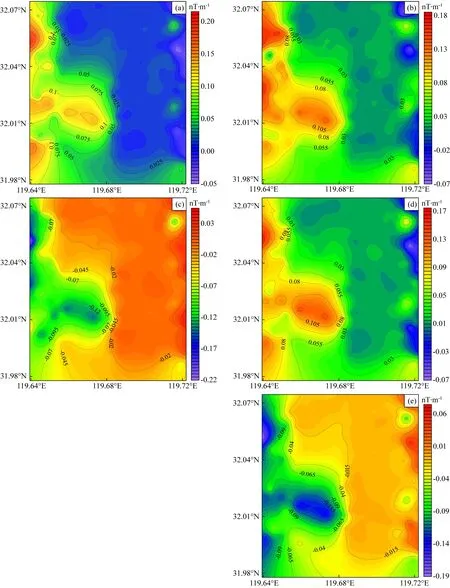
图11 200 m飞行高度全张量磁梯度测量结果(a)Gxx；(b)Gxz；(c)Gyx；(d)Gyz；(e)Gzz.Fig.11 Results of full tensor magnetic gradient measurement at 200 m flight altitude

4.3 重复线飞行测试

为了进一步验证系统测量结果的稳定性、准确性以及对于同一测线前后两次测量结果的一致性，进行了200 m高度重复线飞行试验，对于相同的航迹，前后两次测线的测量结果得到的全张量5个独立分量的前后对比效果图如图12所示.

由图12可知，对于同一条测线，前后两次测量结果的5个独立分量的总体变化趋势保持一致，进一步验证了测量系统的稳定性，两条测线结果不完全重合的原因有三个：(1)飞机的飞行高度在两条测线上的坐标会有差异；(2)两条测线上的测点难以保证完全重合；(3)系统噪声影响.

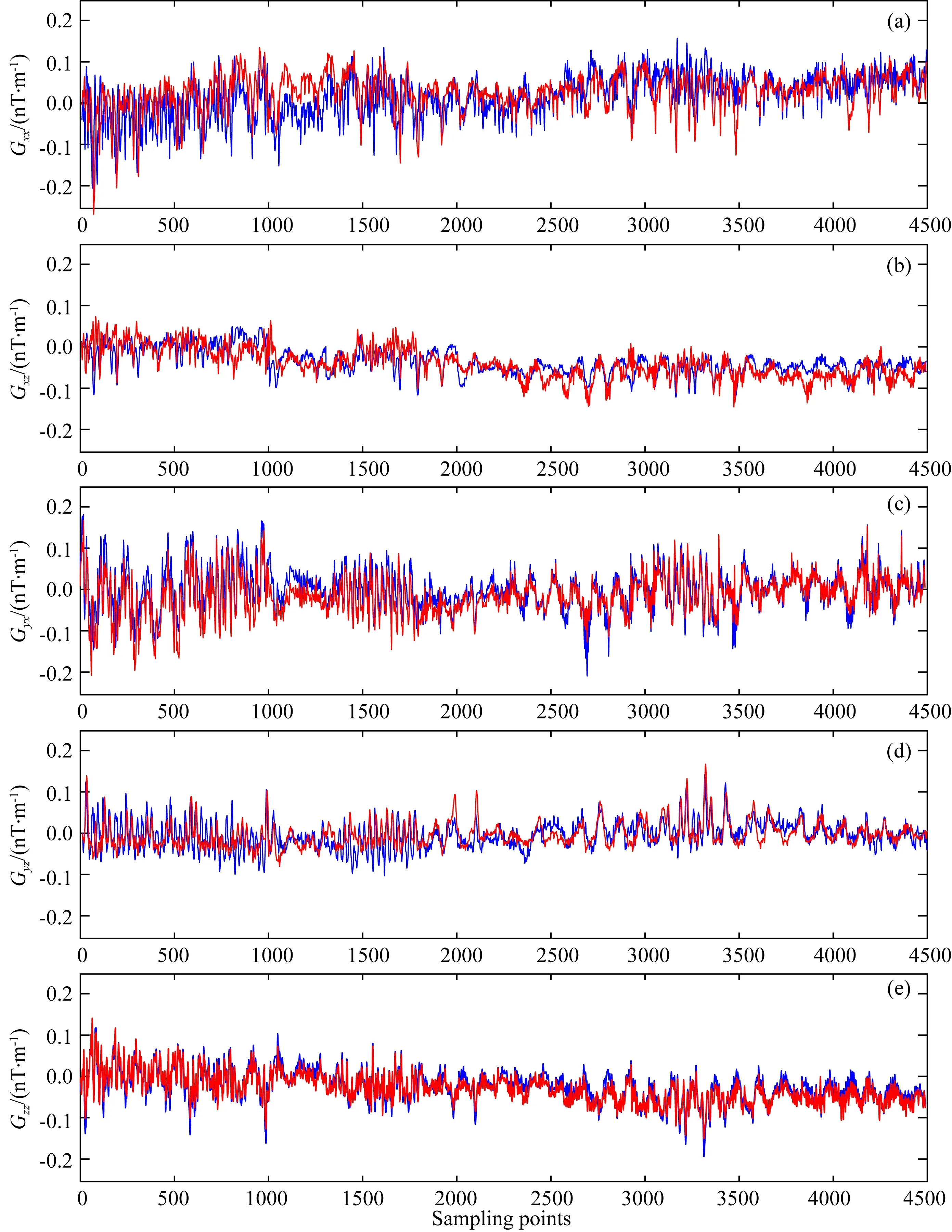
图12 全张量5个独立分量的重复线测试结果对比图Fig.12 Comparison of five independent components of the full-tensor of repeated flight surveys

5 结论

成功研制的吊舱式高温超导全张量磁梯度测量仪工程样机在江苏省丹阳市试验区开展了飞行试验，获取试验区全张量磁梯度分布图，测试结果表明吊舱式高温超导全张量磁梯度测量仪各项指标满足《航空磁测技术规范》(DZ/T 0142-2010)(中华人民共和国国土资源部,2010)的要求，具备了实际生产的能力，推动了我国航磁勘探的进步与发展，能够为航磁多参量数据采集-处理-解释系统提供宝贵的实测数据，填补我国航空高温超导全张量磁梯度测量技术研究的空白，缩短与发达国家在该技术上的差距，为“深地资源勘查开采”提供先进技术支撑，具有很好的应用前景.

致谢本文研究工作是在中国自然资源航空物探遥感中心多年工作基础上完成的，凝聚了前人智慧与结晶，同时，也得到了吉林大学等科研院校的大力支持，在此表示衷心的感谢.感谢审稿专家提出宝贵的修改意见.