大规模高帧频读出电路高速数据传输模型研究

叶联华，刘 煦，李云铎，黄松垒，黄张成

大规模高帧频读出电路高速数据传输模型研究

叶联华1,2,3，刘 煦1,2,3，李云铎1,2，黄松垒1,2，黄张成1,2

（1. 中国科学院上海技术物理研究所 传感技术联合国家重点实验室，上海 200083；2. 中国科学院上海技术物理研究所 中国科学院红外成像材料与器件重点实验室，上海 200083；3. 中国科学院大学，北京 100049）

本文针对大规模高帧频读出电路的数字信号输出建立了高速数据传输模型。首先由集总参数模型得到传输电路3dB带宽及响应时间常数与各器件参数之间的关系，指明了输出级MOS管的尺寸及传输线负载是决定高速时域响应特性的关键参数。进一步采用分布参数模型，利用Elmore延时模型更精确地确定了响应时间常数的数学解析式，获得了可使带宽最大化的输出级尺寸的最优设计。仿真结果表明，在典型的64×64面阵功耗和面积约束条件下，优化后传输门和复合逻辑门两种三态传输电路的输出3dB带宽分别可达293MHz和395MHz。

大规模高帧频读出；数据传输模型；Elmore延时模型

0 引言

为提升探测视场和空间分辨率，以适应不断发展的红外应用需求，大规模焦平面探测器应运而生。为了提高实时获取数据的能力，高帧频读出成了不可或缺的设计，从而迅速推高了焦平面对数据传输速率的要求。以单光子焦平面为例，大规模阵列的数据输出速率要求已达Gbps以上[1-3]。为了实现大规模阵列的高帧频读出，研究人员提出了许多方案，主要聚焦于减少总线输出的数据量，例如多通道总线输出、数据压缩[3-4]、事件驱动读出架构[5-6]、感兴趣区域读出[7-8]等。

即便如此，由于帧频的进一步提高，以及面阵规模进一步增大，面阵内总线高速数据传输仍然面临着巨大的压力。由于受读出电路功耗、版图面积等的限制，同时受总线寄生电容、与总线相连的器件寄生电容的影响，总线带宽往往受限。这导致高速数据输出时信号响应时间常数可能会接近于码元宽度，因此可能会发生码间串扰导致信号畸变、展宽，从而在数据恢复过程中产生误码。随着阵列规模继续增大，寄生电容及寄生电阻也随之等比例增加，导致输出带宽越发恶劣，因此如何实现数据高速输出是未来更大规模高帧频读出研究的主要技术障碍之一[8-9]。

为了解决大规模高帧频读出电路高速数据输出面临的难题，需要为总线传输电路建立精确的带宽和响应时间常数的分析模型。本文介绍了一种传输电路的高速时域响应特性分析模型。

1 传输电路结构

由于受像素大小、面阵规模的限制，总线和隔离器件的寄生电容会导致传输带宽减小，高频分量在传输过程中被丢失，信号翻转过程变得十分缓慢，数据高速传输难以实现。如何提高传输电路的高速数据输出能力是读出电路设计的难题之一。

其中一个方案是采用驱动能力更强的驱动器。或者采用低压差分传输等技术，这种技术在提高数据传输速率方面效果十分明显。但是，像元中驱动能力更强的驱动器往往消耗更多功耗，这将使得整个阵列功耗大幅上升。而低压差分传输技术往往电路结构较复杂，版图面积较大，难以集成到读出电路像素中，加之需要的总线资源也随之翻倍，并不适用于大规模高帧频读出电路数据读出。因此，像素高速数据输出电路必须结构尽量简单，同时具备能满足特定数据输出速率要求的带宽。

本文中采用了两种结构简单的典型三态电路进行建模分析，一种是基于传输门的三态电路，一种则是基于复合逻辑门的三态电路，电路结构如图1。

2 传输线集总模型下的带宽和延时分析

2.1 基于传输门的三态电路

缓冲器由两级反相器构成，由于信号由第一级反相器输入到第二级反相器输入的延时很短，为简化分析，我们只需研究第二级反相器经传输门到达远端输出节点的传输延时。在本电路中，反相器作为驱动级，传输门作为输出级。

传输门可等效为一个电阻。当输入切换为低电平时，其集总等效电路如图2（忽略线电阻，OUT为输出节点总寄生电容，由传输线寄生电容及传输门输出节点寄生电容组成）。

根据基尔霍夫电压电流关系可得到传输函数：

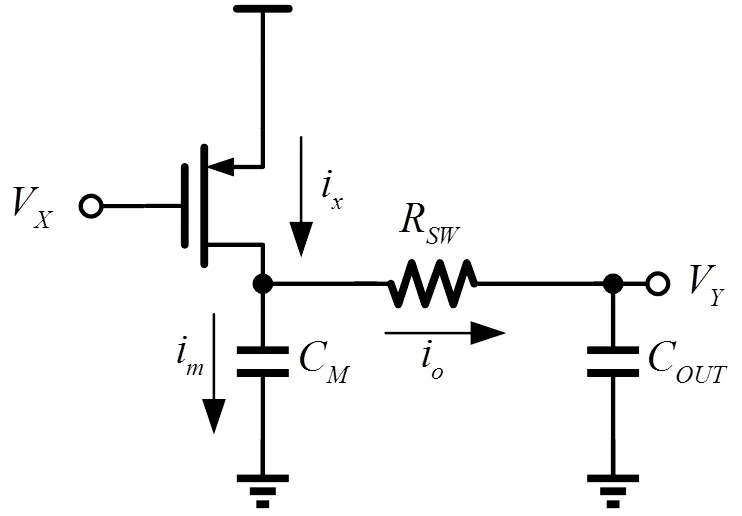
图2 传输门结构驱动和输出级的集总等效电路

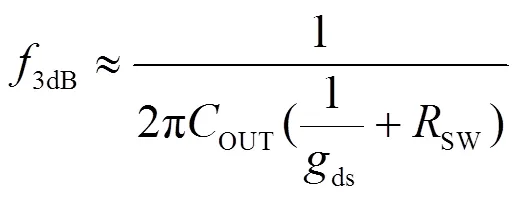
式中：OUT＝L＋TG，L为传输线寄生电容；TG为传输门的寄生电容。因此响应时间常数为：

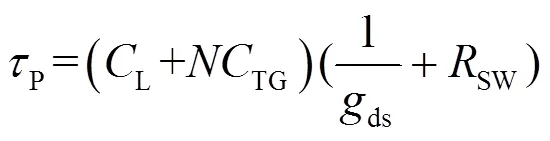
根据式(2)和(3)，输出带宽和响应时间常数主要由ds、L及SW决定。其中ds主要由电流决定。提高电流从而增大ds可以显著减小响应时间常数、提高输出带宽；然而1/ds与SW相当时，继续增大充放电电流的作用将不再理想。如图3是典型设计参数下响应时间常数与充放电电流的关系。

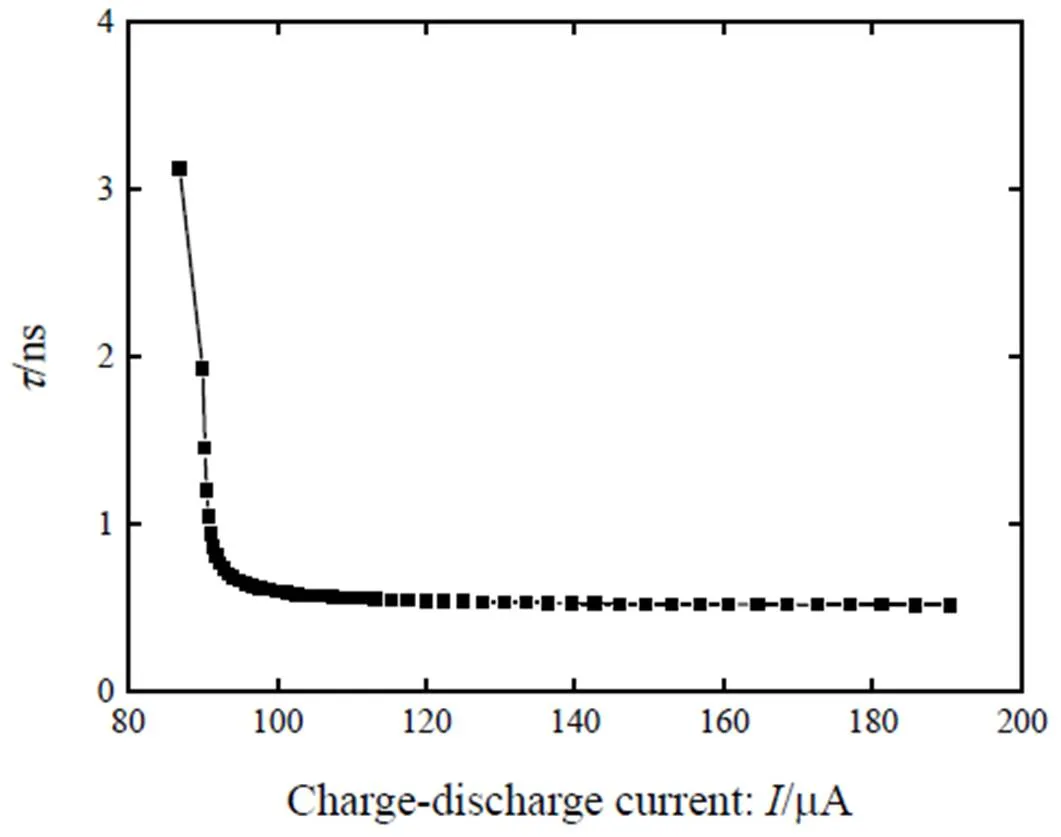
图3 响应时间常数与充放电电流的关系

在电流不变的情况下，传输门导通电阻和输出节点总寄生电容成为决定传输带宽的关键参数。减小SW通常以增大传输门尺寸为代价，但这将会导致传输门带来的寄生电容也成倍增加，因此传输门尺寸可能存在一个最优值，使得响应时间最小，带宽最大。

2.2 基于复合逻辑门的三态电路

与前述分析一样，对基于复合逻辑门的三态电路，我们也只对驱动和输出级进行建模分析，其充电时的等效电路如图4，其中FET为输出级MOS对的寄生电容。在本电路中，驱动级和输出级是一体的，即复合门与总线相连的两个MOS管。

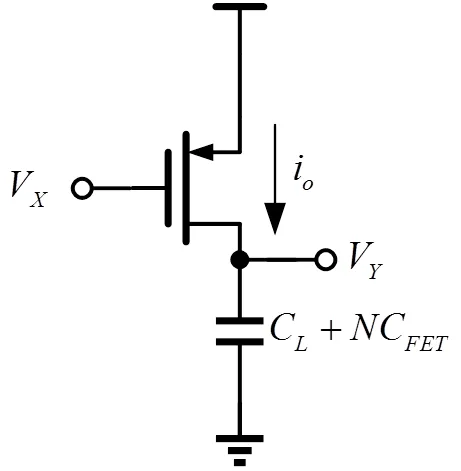
图4 复合逻辑门结构驱动和输出级的集总等效电路

根据基尔霍夫电压电流关系得到传输函数：

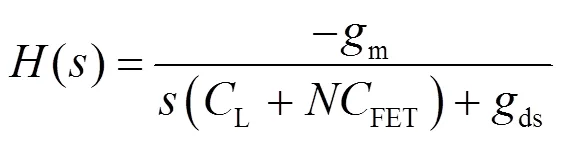
其3dB带宽为：

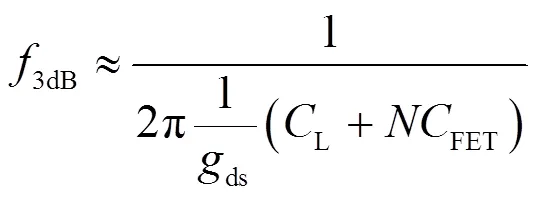
以P代替1/ds，则响应时间常数为：

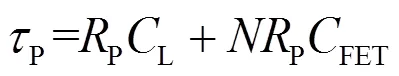
式中：PFET为零负载延迟项；PL为负载延迟项。若输出级尺寸扩大倍（宽扩大倍，长不变），则FET→FET，P→P/，可见尺寸扩大倍零负载延迟项不变，但可使负载延迟项减小倍。当L与FET相当或者L＞FET时，尺寸扩大倍可显著减小上升下降时间；而当L远小于FET时，对延迟降低的作用将不明显。

3 传输线分布参数Elmore延时分析

集总模型忽略了传输线分布参数效应的影响，在小面阵、传输线长度较短时能快速得到较为准确的结果，然而在大面阵、长传输线场景中，只能得到定性的结论，因此还需进一步采用分布参数模型进行分析。

3.1 基于传输门的三态电路的延时分析

根据像元数建立传输线π(－1)模型，即两相邻像元间的传输线电阻为line，最外侧像元处的传输线寄生电容为line/2，其余像元处传输线寄生电容为line，则L＝(－1)line，L＝(－1)line。其中L、L分别为传输线的电阻和寄生电容。第个像元（1≤≤）输出的等效树形结构延时链如图5。

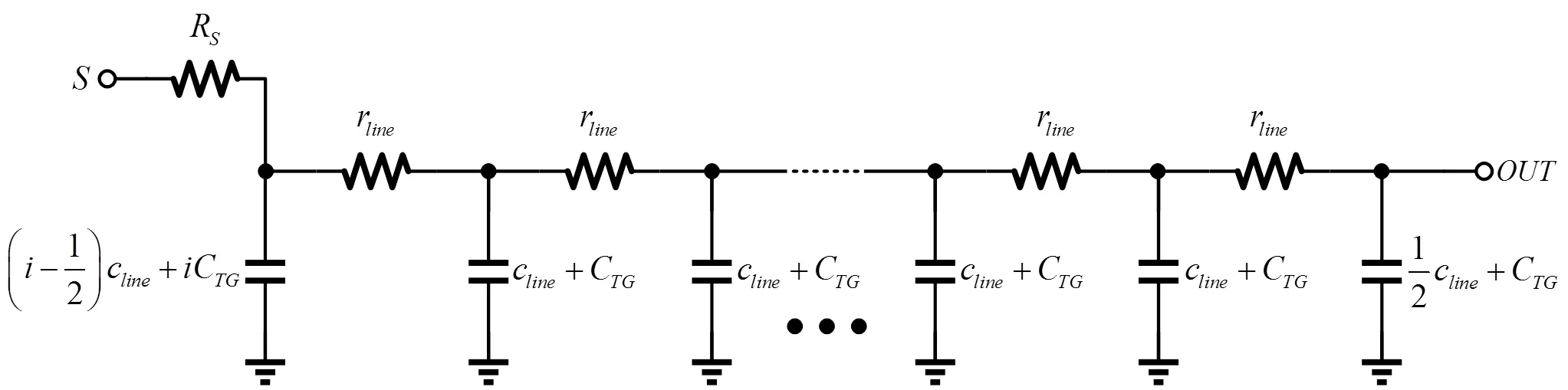
图5 第i个像元输出的等效树形结构RC链

图中S＝1/ds＋SW。以op代替1/ds，根据Elmore延时公式，其响应时间常数如式(7)：

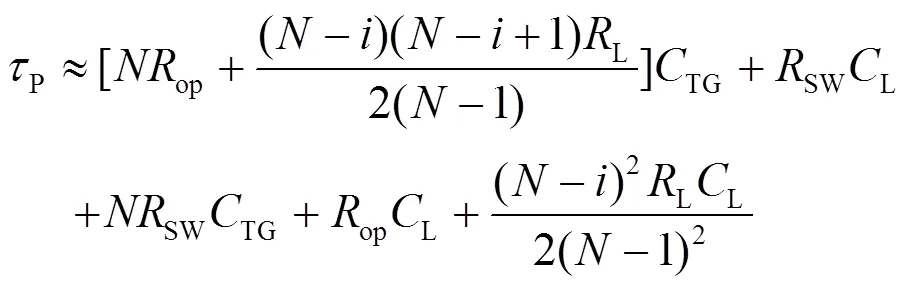
对第1像元（＝1），若忽略传输线电阻L，则响应时间常数为P≈SL＝(L＋TG)(op＋SW)，与集总模型传函分析结论相同。

长金属传输线的寄生电容为L＝S＋P。其中、分别为传输线的长度和宽度，S为单位面积对地电容，P为单位长度侧壁电容。由探测器阵列规模以及像元中心距决定。典型的0.18mm CMOS工艺中，metal3的S约为0.0088fF/mm2，P约为0.056fF/mm。当传输门尺寸扩大倍，传输线宽度扩大倍时，则TG→TG，SW→SW/，L→(L－p)＋p，L→L/，系统的一阶时间常数如式(8)所示：

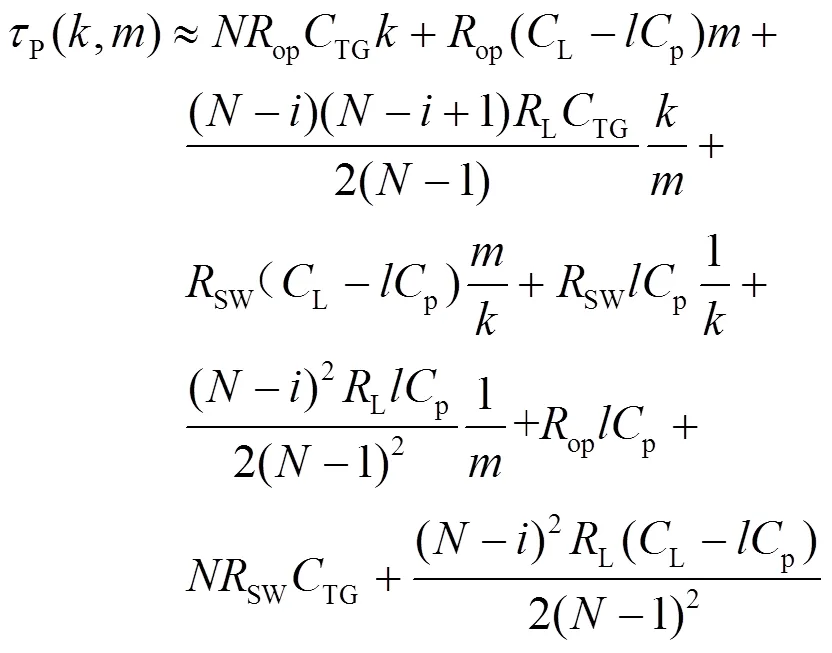
3.2 基于复合逻辑门的三态电路的延时分析

与前述分析类似，对第个像元（1≤≤）而言，根据Elmore延时公式，其响应时间常数如式(9)：

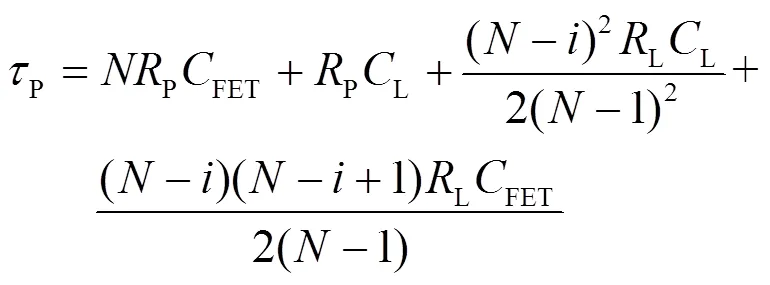
忽略线电阻L，可得到与集总模型一致的结论。若输出级尺寸扩大倍（宽扩大倍，长不变），则FET→FET，P→P/，可得出P关于的解析式。P存在最小值，其最小值在：

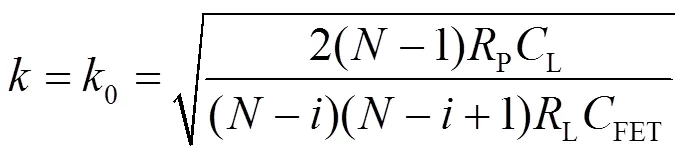
时取得。＝0时系统的响应时间常数P最小，3dB带宽最大。对于第1个像元，像元数每增大一倍，由于L、L和均增大一倍，最优设计尺寸0将缩小为原来的约0.707倍。

分布模型分析结果表明这种电路结构下设计存在最优值，可以使得响应时间常数最小，带宽最大。最优值设计是否值得采用仍然需视具体情况而定，由于输出级的功耗随尺寸增大线性增加，当最优值对应的尺寸过大时，功耗的大幅增加换来并不明显的速度提升显然是不明智的。仿真表明，最优值设计下采用这种电路结构速度比采用传输门的电路结构提升可达约30%，而且由于最优设计尺寸会随像元数量增加而减小，这种结构更适用于大规模面阵的数据输出。

考虑线宽的影响，当驱动级尺寸扩大倍，传输线宽度扩大倍时，则FET→FET，P→P/，L→(L－p)＋p，L→L/，系统的一阶时间常数如式(11)：

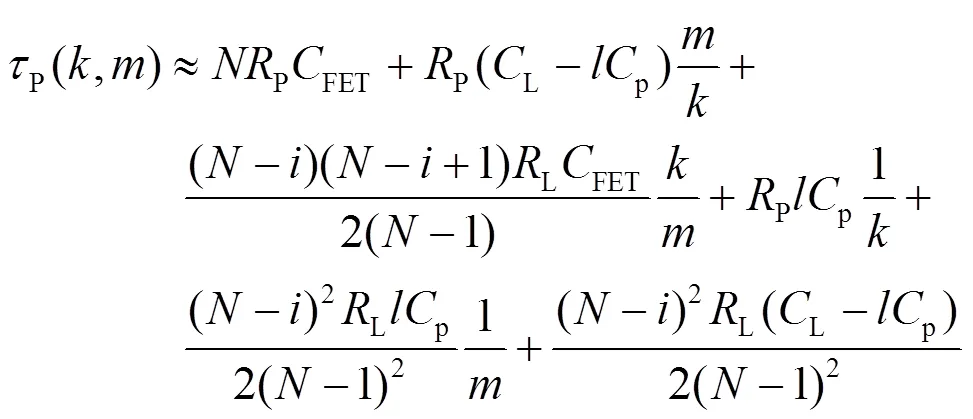
4 仿真结果及分析

式(8)和(11)分别对两种三态电路的响应时间常数进行了定量描述，从式中可见，一阶时间常数随的增大而减小，即越靠近右端输出节点的像元其输出带宽越大。设计时以第1像元的最优设计尺寸为准。

4.1 基于传输门的三态电路

为减小高速信号输出时的占空比失真，反相器和传输门均采用电气对称设计，典型0.18mm工艺条件下PMOS和NMOS宽长比之比约为2.5。初始设计中反相器和传输门均采用最小尺寸电气对称设计，即n/n＝220nm/180nm，p/p＝550nm/180nm；传输线宽度采用设计规则允许的最小尺寸（0.28mm）。像元给传输电路的面积预算最大能容许的反相器尺寸为p＝25mm。由式(8)可知，式中所有的参数实际上取决于反相器、传输门及传输线的设计尺寸。

首先考虑传输线的影响。如图6是仿真得到的输出带宽随传输线宽度变化的曲线。反相器及传输门的尺寸较小时，它们的导通电阻远大于传输线电阻，此时传输线寄生电容成为影响输出带宽的主要因素，因此带宽最大值将在传输线宽度较小时取到。随着反相器及传输门的尺寸增大，传输线电阻的影响逐渐不可忽视，传输线宽度的最优值逐渐增大。由于传输线寄生电容中侧壁电容占比非常大，成倍增大金属线的宽度仅会使电容略微增加，因此带宽在达到最大值后会随传输线宽度的增加缓慢下降。

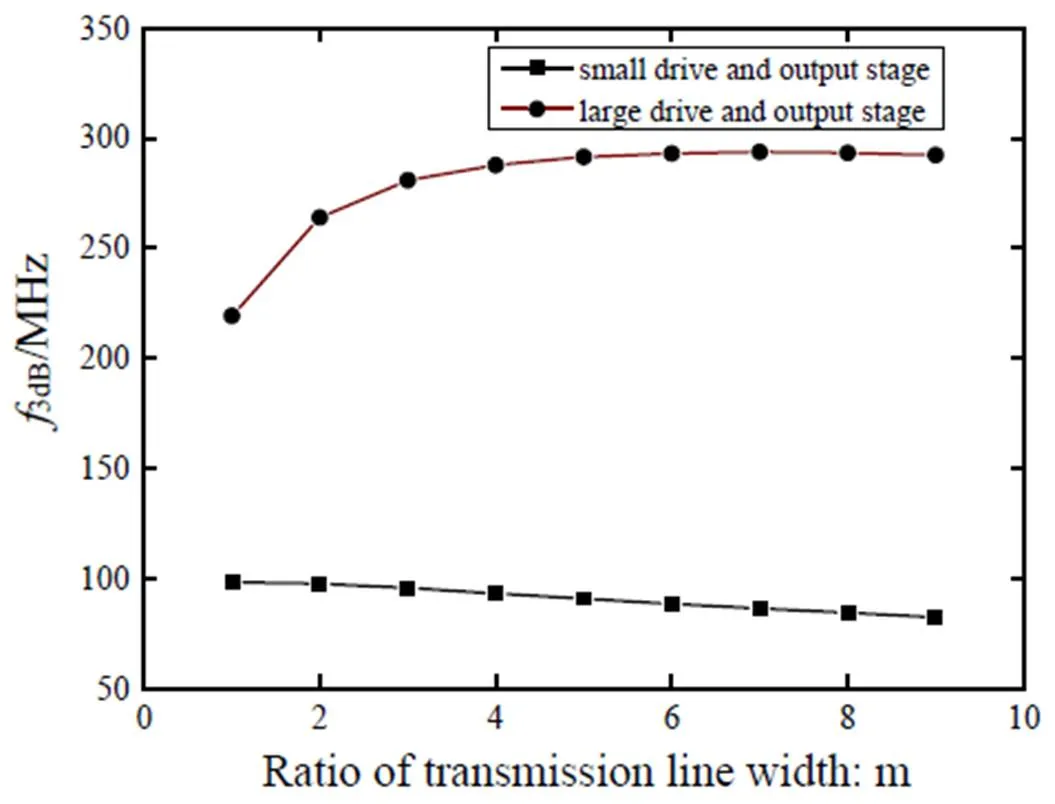
图6 输出带宽与传输线宽度的关系曲线

由于输出带宽在达到最优值后下降十分缓慢、最优值变化范围较小，我们取一个设计范围内最大的最优值作为固定尺寸，考虑在传输线宽度固定时反相器及传输门尺寸对带宽的影响。图7是仿真所得不同反相器尺寸下输出3dB带宽与传输门尺寸的关系曲线。

比较图7中的不同曲线可发现，p按照等差变化，而相邻曲线的间隔随着p变大而减小。这说明若传输门尺寸一定（值一定），反相器尺寸p比较小时，增大p对于增大输出带宽效果显著，而p较大时这种作用不再明显。这与集总分析结论一致。

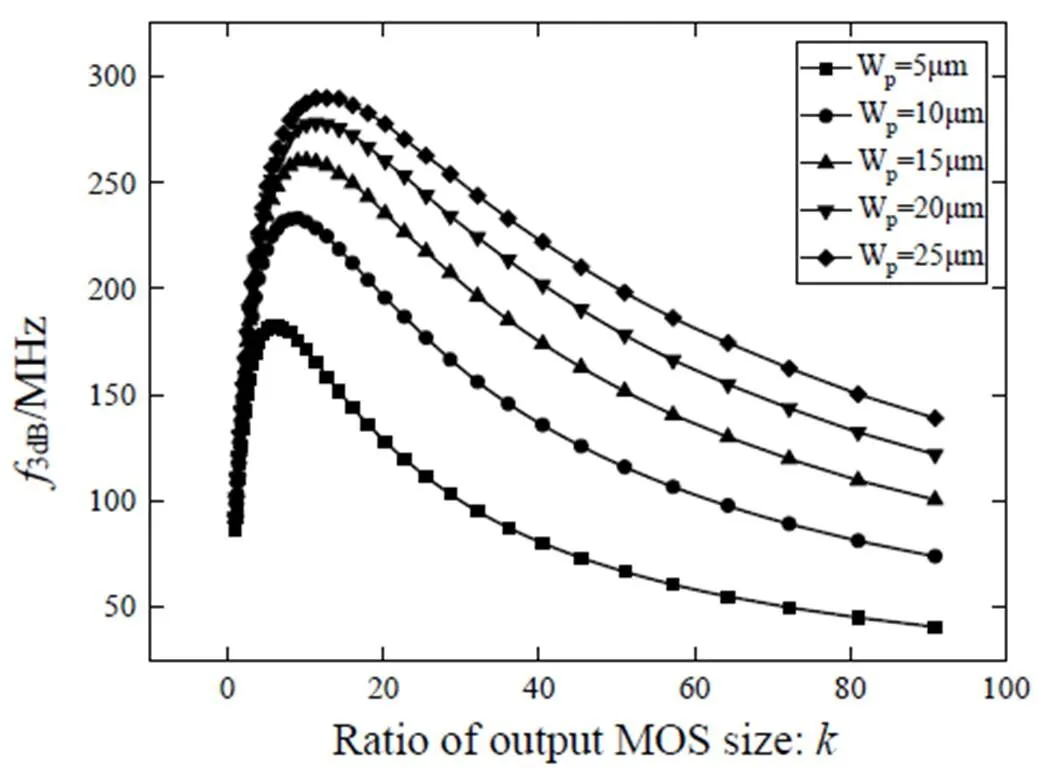
图7 3dB带宽与传输门尺寸的关系曲线

反相器尺寸固定时，输出带宽存在着一个最大值。随着传输门尺寸变大，输出带宽迅速上升至最高值（293MHz），而后下落。输出带宽最大值所对应的传输门尺寸最优值随着反相器尺寸的增大而增大。但是相对于反相器尺寸的变化，传输门最优值的变化幅度比较小，对于反相器尺寸p由5mm增大为25mm，对应传输门的p最优值仅由3.5mm（＝6.36）增大为7mm（＝12.73）。

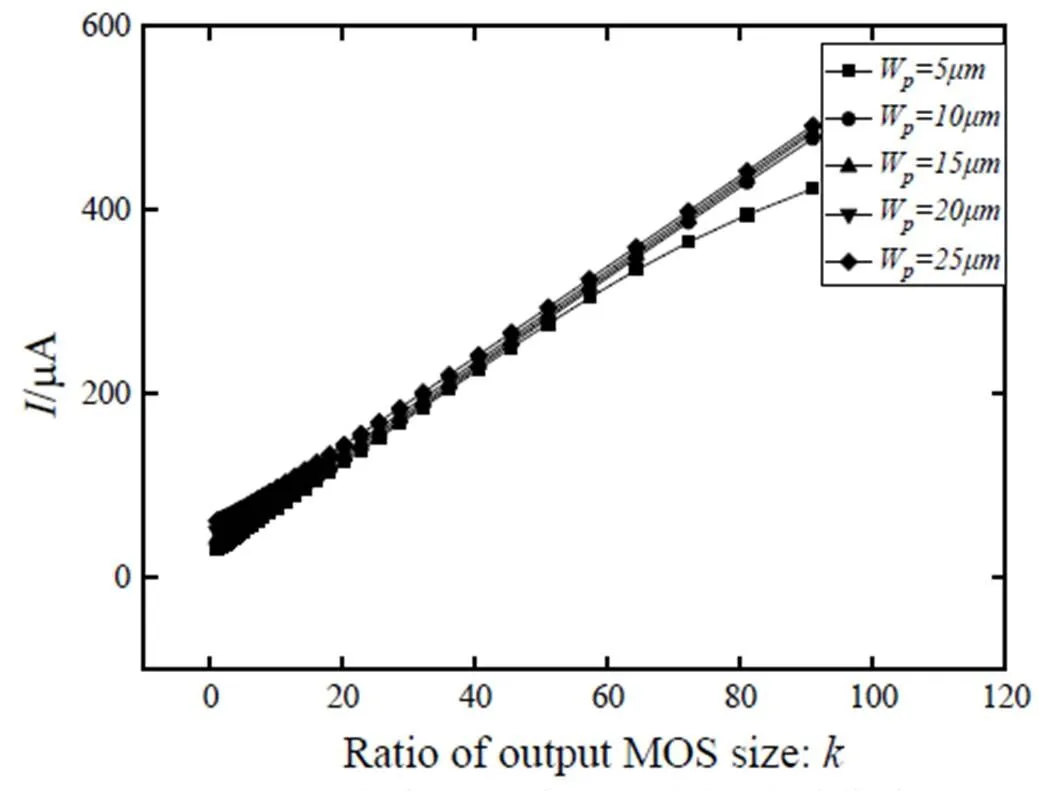
图8 平均电流与传输门尺寸的关系曲线

图8是不同反相器尺寸下平均电流与传输门尺寸的关系曲线，输入为50MHz时钟信号。比较图8中不同反相器尺寸下平均电流与传输门尺寸的关系曲线，传输门尺寸相同时各曲线间相差很小，这说明反相器尺寸增大对于平均功耗的贡献有限，这是由于功耗主要由动态功耗组成，传输门尺寸一致时总线节点寄生电容一致，因此功耗相差不大。相对而言，功耗对传输门尺寸变化更加敏感，平均电流随着传输门尺寸的增大迅速增加。反相器尺寸增大，功耗略微上升的原因可能是由于中间节点电容M的增大及电流增大导致的充放电过程中的热损耗增加。

4.2 基于复合逻辑门的三态电路

驱动级初始设计尺寸与前述结构中的反相器、传输门一致，传输线采用最小宽度。如图9是仿真所得的不同驱动级尺寸下输出带宽及平均电流与传输线宽度的关系曲线。

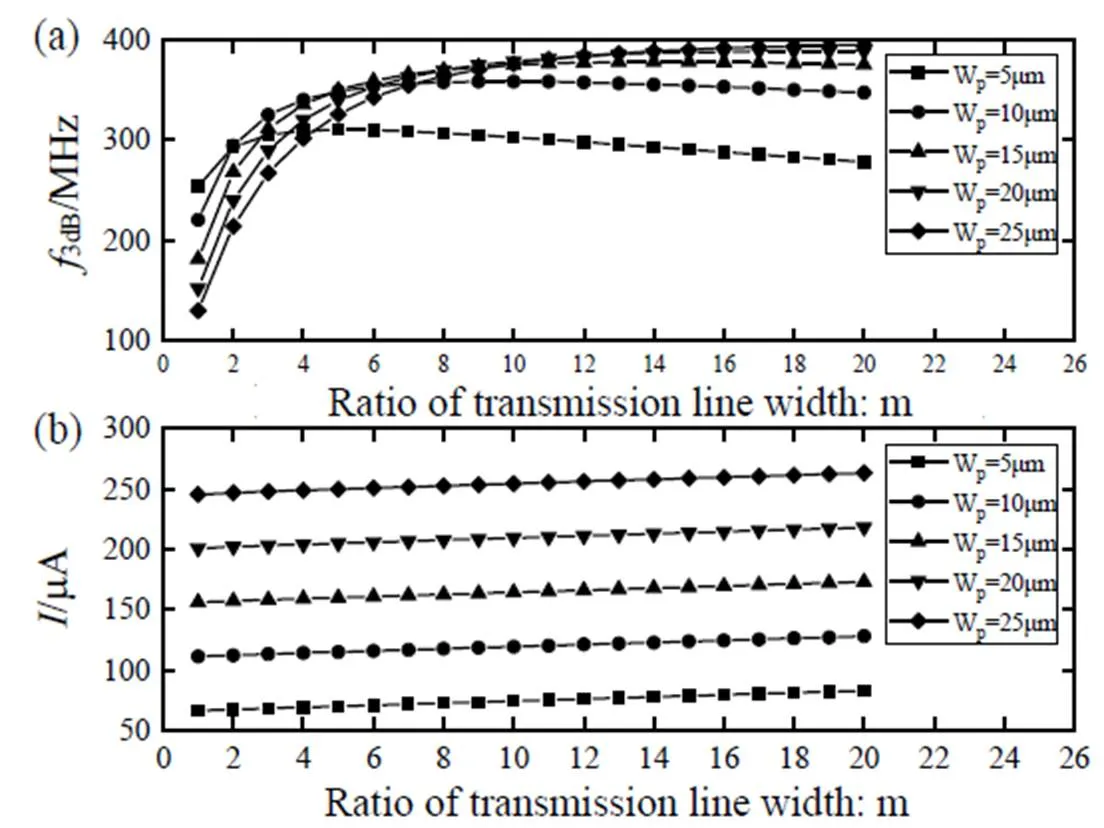
图9 传输线宽度对输出带宽（a）和平均电流（b）的影响

与传输门结构类似，随着驱动级尺寸的增大，传输线宽度的最优值也随之增大，输出带宽在最优值（395MHz）之后缓慢下降，但是相比而言在本结构中最优值的变化范围要大得多。这是因为少了传输门串联电阻的影响，同一驱动级尺寸下，传输线电阻要减小到与驱动级电阻相当，需要更大的宽度。传输线宽度较小时，更大的驱动级反而会使带宽减小，这是由于传输线电阻太大，而更大的驱动级会引入更大的电容，使得延时恶化。

传输线宽度增大对平均电流的贡献很小，这是由于对地电容的占比太小，宽度增大带来的电容增加非常有限，因此平均电流上升缓慢，基本不变。需要注意的是，高频传输时，由于趋肤效应的存在，大宽度金属线电阻与尺寸的关系将偏离理想曲线。考虑趋肤效应带来的阻抗增加的影响，线宽不宜过宽。典型工艺参数下，1GHz时导线宽度不应大于5.2mm，否则会使得趋肤效应较为明显[10]。

4.3 两种传输电路的比较

如图10是最优设计参数下两种传输电路输出带宽随电流的变化曲线，采用最优设计使两种传输电路的3 dB带宽分别可达293 MHz和395 MHz。图中TG代表传输门结构，TSG代表复合逻辑门结构。对于每条曲线，从最左的点开始，图示的46个点分别代表驱动级尺寸为＝1, 2, 3, …, 46。可见，从纵向来看，在同样的平均电流下，复合逻辑门结构可实现更大的输出带宽，而且驱动级尺寸更小。从横向来看，实现同样的带宽，复合逻辑门结构不仅驱动级更小，而且功耗更低。

从电路结构上来说，传输门结构仅需8个MOS管，而复合逻辑门结构需12个。因此，在对面积要求十分苛刻且对带宽要求较低的场合中，传输门结构可能更合适。

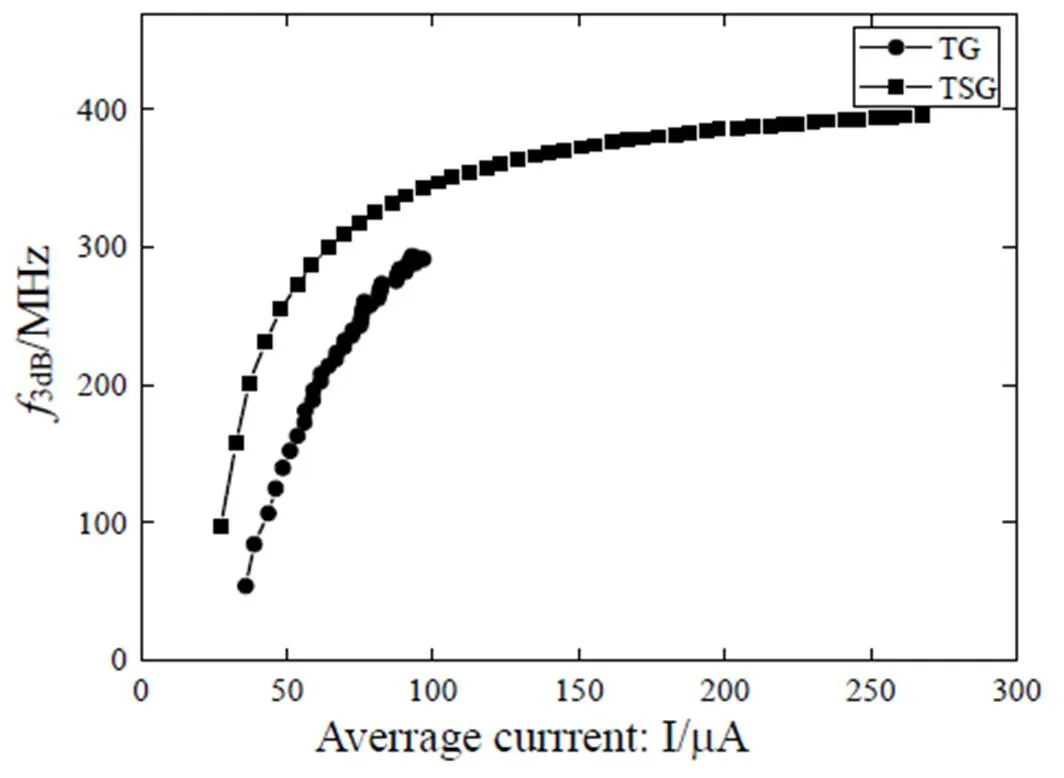
图10 最优设计下输出带宽随平均电流的变化曲线

5 结论

本文通过传输线集总参数模型和传输线π(−1)模型下的Elmore延时模型，为大规模高帧频读出电路的两种典型高速数据传输电路建立了带宽和响应时间常数的分析模型，并在此基础上找到了对传输电路带宽进行优化的设计方法。研究结果表明，采用输出级及传输线的最优设计尺寸，可以有效提高输出带宽。仿真和计算结果表明，在典型0.18mm CMOS工艺及本文特定的功耗、面积限定条件下，采用最优设计使两种传输电路的3dB带宽分别可达293MHz和395MHz。总体而言，复合逻辑门结构的传输电路在带宽和功耗等性能指标上优于传输门，更适用于大规模面阵的数据输出。

本文所建立的传输电路带宽及响应时间常数模型对于数字信号高速传输设计具有一定的参考意义。采用本模型进行计算可以直接、快速地获得相关器件的最优设计尺寸，在一定程度上为解决大规模高帧频读出电路数据高速传输问题提供了一种方案。

[1] Richardson J, Walker R, Grant L, et al. A 32× 32 50ps resolution 10 bit time to digital converter array in 130nm CMOS for time correlated imaging[C]//, 2009: 77-80.

[2] Gersbach M, Maruyama Y, Trimananda R, et al. A time-resolved, low-noise single-photon image sensor fabricated in deep-submicron CMOS technology[J]., 2012, 47(6): 1394-1407.

[3] Field R M, Realov S, Shepard K L. A 100fps, time-correlated single-photon-counting-based fluorescence-lifetime imager in 130 nm CMOS[J]., 2014, 49(4): 867-880.

[4] YANG X, ZHU H, Nakura T, et al. A 15×15 single photon avalanche diode sensor featuring breakdown pixels extraction architecture for efficient data readout[J]., 2016, 55(4S): 04EF04.

[5] NIE K, WANG X, QIAO J, et al. A full parallel event driven readout technique for area array SPAD FLIM image sensors[J]., 2016, 16(2): 160.

[6] Shawkat M S A, Mcfarlane N. A digital CMOS silicon photomultiplier using perimeter gated single photon avalanche diodes with asynchronous AER readout[J]., 2020, 67(12): 4818-4828.

[7] Buchholz J, Krieger J, Bruschini C, et al. Widefield high frame rate single-photon SPAD imagers for SPIM-FCS[J]., 2018, 114(10): 2455-2464.

[8] Aull B F, Duerr E K, Frechette J P, et al. Large-format geiger-mode avalanche photodiode arrays and readout circuits[J]., 2017, 24(2): 1-10.

[9] Cominelli A, Acconcia G, Peronio P, et al. Readout architectures for high efficiency in time-correlated single photon counting experiments-analysis and review[J]., 2017, 9(3): 1-15.

[10] Rabaey J M, Chandrakasan A P, Nikolić B.[M]. Upper Saddle River, NJ: Pearson education, 2003.

Research on High-Speed Data Transmission Model of Large-Format High-Frame-Rate Readout Integrated Circuit

YE Lianhua1,2,3，LIU Xu1,2,3，LI Yunduo1,2，HUANG Songlei1,2，HUANG Zhangcheng1,2

(1. State Key Laboratory of Transducer Technology, Shanghai Institute of Technical Physics, Chinese Academy of Sciences, Shanghai 200083, China;2. Key Laboratory of Infrared Imaging Materials and Detectors, Shanghai Institute of Technical Physics, Chinese Academy of Sciences, Shanghai 200083, China;3. University of Chinese Academy of Sciences, Beijing 100049, China)

In this paper, a high-speed data transmission model is presented for the digital signal output of a large-format high-frame-rate readout integrated circuit. We utilize the lumped parameter model to investigate the relationship between 3dB bandwidth, response time, and device parameters. It is indicated that the size of the driver and the load of the transmission bus are the key parameters that determine the high-speed time-domain response characteristics. Furthermore, by using the distributed parameter model and Elmore delay model, the analytic expression for response time is deduced with more accurate values, and the optimal design of the output stage toward maximum bandwidth is obtained. Under the typical constraint condition of layout and power dissipation in a 64×64 array, simulation results show that the output 3dB bandwidth of the transmission gate and composite logic gate can reach 293MHz and 395MHz, respectively.

large-format high-frame-rate readout integrated circuit, data transmission, Elmore delay model

TN402

A

1001-8891(2022)01-0066-07

2020-12-07；

2022-01-08

叶联华（1995-），男，硕士研究生，主要研究方向为单光子焦平面读出电路设计。E-mail: yelianhua0219@163.com。

黄张成（1985-），男，副研究员，主要研究方向为光电传感器专用集成电路设计及高光谱短波红外探测器研制。E-mail: huangzc@mail.sitp.ac.cn。

上海市自然科学基金（19ZR1465500）。