有理分式不定积分新解
2022-01-24董丽萍
董丽萍,曾 晶
(福建师范大学数学与统计学院,福建 福州 350117)
数学分析课程中的定积分在计算平面图形的面积、体积、平面曲线的弧长,压力、引力等物理量,以及常微分方程和多元积分学的计算中都至关重要.不定积分被积函数类型多样,如指数函数、对数函数、有理分式、三角函数有理式和某些无理根式等.其中,求解有理分式不定积分的方法较多、技巧性强.由于有理假分式可以转化为一个多项式和有理真分式之和,因此有理分式不定积分的计算主要是有理真分式不定积分的计算,这是本文主要的讨论对象,其一般形式为
(1)
其中n,m为非负整数,n>m≥0,ai,bj(i=0,1,…,n;j=0,1,…,m) 均为常数,且an≠0,bm≠0.
计算有理分式不定积分的常用方法有凑微分法、换元法、分部积分法等.这些方法在一些数学教材[1-3]中都有详细的介绍,但不能解出任意有理分式不定积分,有些虽然可以解出,却步骤繁琐.一直以来,数学研究者们不断寻求各种简便方法计算有理分式的不定积分,如吴春[4]提出对分母无重根的有理分式,直接运用积分规则积分;对分母有重根的,先化有理分式为无重根的形式再积分;对分母次数远大于分子次数的,先作变量替换,再积分等技巧.李鸿儒[5]提出拆项法,徐英杰等[6]运用配项和凑微分的方法避免了分解有理分式和求解系数的繁杂步骤.刘玉娟等[7]根据递推公式和三角代换将有理分式化为三角函数有理式,然后由三角函数的关系式化简求解.顾丽娟等[8]将部分分式积分法的计算步骤合并,整理出一个统一公式,利用公式直接计算.
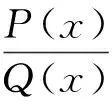
(2)
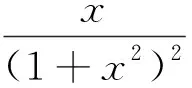
1 预备知识和定理
定义1[12]设f(x)、g(x)是两个实系数多项式,若满足如下条件:
(1)d(x)是f(x)、g(x)的公因式.
(2)f(x)、g(x)的公因式全是d(x)的因式,则d(x)称为f(x)、g(x)的一个最大公因式.
记(f(x),g(x))为f(x)、g(x)首项系数为1的最大公因式.
定义2若(f(x),g(x))=1,则f(x)与g(x)称为互素的.
引理1[12]次数≥1的实系数多项式在实数域上可以唯一分解成含一次因式和二次因式的乘积的形式.
引理2[10]设式(1)中Q(x)=Q1(x)Q2(x) …Qs(x),且Q1(x),Q2(x),…,Qs(x)互素,则存在唯一一组多项式P1(x),P2(x),…,Ps(x)使得式(1)化为
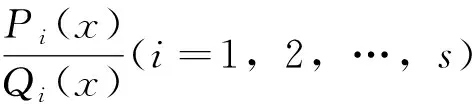
由引理1可知式(1)中的Q(x)可以分解为
Q(x)=an(x-d1)s1(x-d2)s2…(x-dr)sr(x2+e1x+f1)k1(x2+e2x+f2)k2…(x2+etx+ft)kt.
(3)
由于Q(x)具有式(3)中形如(x-di)si和(x2+eix+fi)ki的因式,定理1和定理2分别对Q(x)只含有这两类因式的情形进行分解.定理3对一般形式的Q(x),即式(3)给出分解方法.
定理1若Q(x)=an(x-d)n,P(x)为m( 其中An-i(i=0,1,…,m)为常数. 证明 根据泰勒展开公式,有 等式两边同时除以an(x-d)n得 注1有理分式分解通常采用文[2]的方法,当式(1)的Q(x)形如an(x-d)n时,其分解式形如式(2),共有n项.由定理1知P(x)泰勒展开的项数为m+1项,因此式(1)分解的项数为m+1项,有效减少了求解步骤. 定理2若式(1)中Q(x)=an(x2+ex+f)l,其中e2-4f<0.P(x)为m(<2l)次多项式,则式(1)可化为 证明 作带余除法 P(x)=P0(x)(x2+ex+f)+(E0x+F0), P0(x)=P1(x)(x2+ex+f)+(E1x+F1), P1(x)=P2(x)(x2+ex+f)+(E2x+F2), ⋮ Pλ-2(x)=Pλ-1(x)(x2+ex+f)+(Eλ-1x+Fλ-1), 从而 P(x)=Pλ-1(x)(x2+ex+f)λ+(Eλ-1x+Fλ-1)(x2+ex+f)λ-1+ (Eλ-2x+Fλ-2)(x2+ex+f)λ-2+…+(E0x+F0). 覆盖层是岩溶塌陷产生的物质载体,既是岩溶塌陷的破坏体,又是抵抗岩溶变形塌陷的重要组成部分。覆盖层厚度越薄,岩溶塌陷越发育,分布密度也越大。覆盖层厚度越厚,地下水潜蚀路径越长,土洞扩展到地面的时间也越长,自身容易达到应力平衡,越不容易发生塌陷[11]。据高密度电法测量,研究区东、西侧山沟第四系覆盖层厚度1~8 m,从钻探情况看,表层覆盖层厚度在1~5 m内。 (4) 记Pλ-1(x)=Eλx+Fλ,式(4)两边同时除以an(x2+ex+f)l得 定理3若Q(x)形如式(3),则式(1)可化为 由定理1和定理2得 故 注3定理1和定理2为定理3的特例,分别证明Q(x)只含单个一次因式和二次因式的情形. 推论1任何有理真分式的不定积分都可以归为求以下两种形式的不定积分: (5) (6) 其中d,e,f,E,F均为常数. 注4(1) 推论1由定理3直接得到. (2)文[2]有类似结论,但未证明. (3)式(5)直接计算得 式(6)可化为 (7) 当l=1时,式(7)可化为 当l≥2时,式(7)第二个等号后的第一个不定积分为 对式(7)第二个等号后的第二个不定积分,记 则有递推公式 (8) 综上,式(6)的计算结果为 (9) 其中Il由式(8)给出. 以下给出2个例子说明对分子分母次数相差较大且需要通过分解分式求解的有理分式,其分解的项数较通常做法少. 故 等式两边同乘(x2-x+1)3得 2x2+1=E1x+F1+(E2x+F2)(x2-x+1). 比较两端系数得 E1=2,E2=0,F1=-1,F2=2, 故 故 本文对有理分式不定积分分解为部分分式的过程及计算方法进行了梳理,得到有理分式分解的项数与分子次数的关系,重新给出有理分式分解为部分分式的形式,其分解的形式由分母的形式和分子的次数共同决定.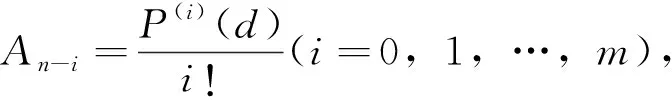
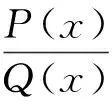
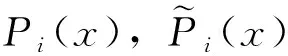
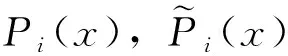
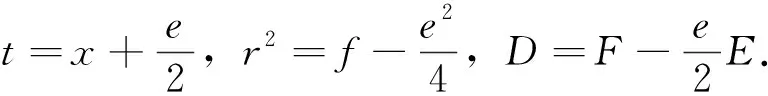
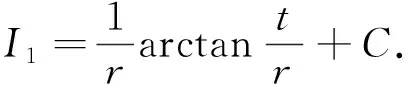
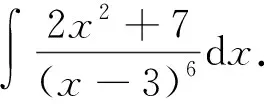


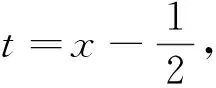
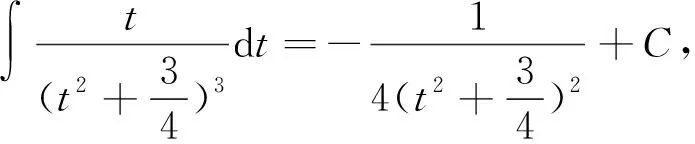
2 结语
