避难所对食物链模型动力学行为的影响*

苏茹燕, 杨文生②③

(①福建师范大学数学与统计学院;②福建省分析数学及应用重点实验室;③福建省应用数学中心(福建师范大学),350117,福建省福州市)

0 引 言

在自然界中,猎物会通过不同方式保护自己免于被捕食者猎杀[1,2]. 环境的异质性能为猎物提供避难所,如枯叶蝶会伪装成枯叶混在落叶中躲避敌害,兔子遇到猎物会伺机找狭小地方隐蔽等. 避难所在一定程度上减少了猎物与捕食者之间的相互作用,增加猎物的数量[3-6].

具有避难所的生态种群模型是种群动力学研究的热点问题之一,目前所研究的具有避难所的生态种群模型大体上可分为两类[7-13]. 一类是避难所保护恒定比例的猎物,如Kar等人[14]研究的以下具有避难所的猎物-捕食者模型

(1)

其中x(t),y(t)分别表示猎物种群和捕食者种群的密度,m∈[0,1)表示避难系数,mx表示被避难所保护的猎物数量. 在此模型中增加避难所的数量会增加猎物的密度. 另一种类型是避难所保护恒定数量的猎物,如Mukherjee[15]研究的以下避难所对3种群食物链影响的模型

(2)

其中x(t),y(t),z(t)分别表示资源生物量,猎物种群和捕食者种群的密度,m是避难所保护的恒定数量的猎物. 在此模型中猎物使用的避难所增加了猎物种群的数量,就捕食者种群而言,当处于平衡水平的猎物密度保持在一定阈值以下时,增加避难所的数量可以降低捕食者的密度.

然而在自然界中,猎物的避难形式多种多样,猎物不仅能依靠环境的异质性躲避猎杀还能依靠捕食者对其天敌的恐惧避难,如在“花→蜂鸟→ 蓝鸦→老鹰”这条食物链中,蜂鸟会选择在老鹰的势力范围内筑巢,由于蜂鸟体格小且灵活,老鹰得消耗很多的能量去捕捉蜂鸟,得到的回报却很少,所以老鹰一般不会捕捉蜂鸟,因此老鹰的势力范围对蜂鸟来说就是避难所. 在这种避难形式下中层捕食者的食饵的避难数量与顶层捕食者的数量成正比. 基于以上例子,本文研究顶层捕食者对中层捕食者的食饵具有保护作用的食物链模型,即

(3)

其中x(t),y(t),z(t)分别代表中层捕食者的食饵,中层捕食者和顶层捕食者的密度,r,k,a1,a2,m,d1,d2,μ,σ均为正数,r表示内禀增长率,k表示环境容纳量,a1为中层捕食者对食饵的捕食系数,a2为顶层捕食者对中层捕食者的捕食系数,m为避难系数,d1,d2分别表示中层捕食者和顶层捕食者的死亡率,μ为食饵的生物量到中层捕食者的生物量的转化系数,σ是中层捕食者的生物量到顶层捕食者的生物量的转化系数.

1 平衡点的存在性和局部稳定性

本节讨论系统(3)的平衡解的存在性和局部稳定性.

首先考虑系统(3)的平衡点的存在性.

(ⅰ)显然系统(3)存在平凡平衡点(0,0,0).

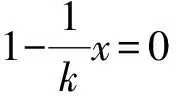
根据韦达定理,方程的两根之和与两根之积分别为

均为正根,其中

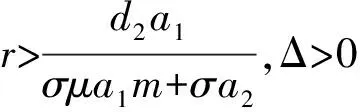
系统(3)的Jacobian矩阵为

(4)

下面证明系统(3)平衡点的局部稳定性.

定理2.1 在系统(3)中

(ⅰ)平凡平衡点E0=(0,0,0)是不稳定的.

(ⅱ)当系统(3)满足(H1):d1>μa1k时,边界平衡点E1=(k,0,0)是局部渐近稳定的.

证明(ⅰ)由(4)式知系统(3)在E0处的Jacobian矩阵为

3特征根为λ1=r,λ2=-d1,λ3=-d2,有一个特征根是正根,因此E0是不稳定的.

(ⅱ)由(4)式知系统(3)在E1处的Jacobian矩阵为

3特征根为λ1=-r<0,λ2=μa1k-d1,λ3=-d2<0. 由假设条件(H1)得λ2<0,因此E1是局部渐近稳定的.

(ⅲ)由(4)式知系统(3)在E2处的Jacobian矩阵为

特征多项式为

其中B,C>0,由假设条件(H2)可得A<0,因此3特征根均有负实部,所以E2是局部渐近稳定的.

(ⅳ)由(4)式知系统(3)在E3处的Jacobian矩阵为

特征多项式为

其中

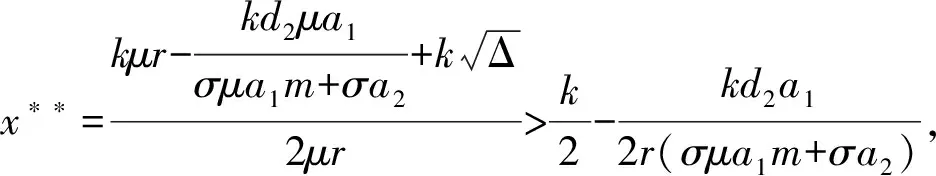
(ⅴ)由(4)式知系统(3)在E4处的Jacobian矩阵为

特征多项式为

其中

由Routh-Hurwitz条件可知,3特征根不全具有负实部,因此E4是不稳定的.

2 平衡点的全局稳定性

本节将通过构造的Lyapunov函数的方法,讨论平衡点的全局稳定性.

定理3.1

(ⅰ)若系统(3)满足(H1),则E1是全局渐近稳定的.

(ⅱ)若系统(3)满足(H2)和(H5):d2>σμa1my*+σa2y*时,边界平衡点E2是全局渐近稳定的.

证明(ⅰ)构造Lyapunov函数

(5)

可知,除了E1外,对任意x,y,z>0,有V1>0,对任意的t>0有

(6)

(ⅱ)构造Lyapunov函数

(7)

可知,除了E2外,对任意x,y,z>0,有V2>0. 对任意的t>0有

(8)

(ⅲ)构造Lyapunov函数

(9)

可知,除了E3外,对任意x,y,z>0,有V3>0,对任意的t>0有

(10)

3 数值模拟

本节将通过数值模拟验证前面得到的理论结果,并说明避难系数的变化对物种数量的影响.

下面先验证前面的理论结果,以下数值模拟的初始条件分别取为:(x(0),y(0),z(0))=(2.5,2,1.5);(2,1.5,1);(1.5,1,0.5).

(ⅰ)当r=2,k=2,a1=2,m=1,μ=0.5,a2=2,d1=4,σ=0.5,d2=1时,系统(3)满足(H1),存在全局吸引的点E1=(2,0,0) 即y种群和z种群灭绝,x种群存活,如图1.

(ⅱ)当r=3,k=4,a1=2,m=0.5,μ=0.5,a2=2,d1=2,σ=0.5,d2=1时,系统(3)满足(H2)和(H5),存在全局吸引的点E2=(2,0.75,0)即z种群灭绝,x种群和y种群稳定共存,如图2.

(ⅲ)当r=2,k=2.5,a1=3,m=1,μ=0.5,a2=2,d1=0.2,σ=0.75,d2=1时,系统(3)满足(H3),存在局部吸引的点E3=(0.9154,0.6667,0.3352) 即3种群共存,如图3.

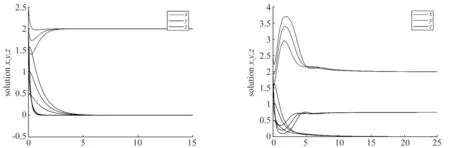
图1 图2

图1：x种群,y种群,z种群如图中所指.r=2,k=2,a1=2,m=1,μ=0.5,a2=2,d1=4,σ=0.5,d2=1, 初始条件分别为:(x(0),y(0),z(0))=(2.5,2,1.5),(2,1.5,1),(1.5,1,0.5).

图2：x种群,y种群,z种群如图中所指.r=3,k=4,a1=2,m=0.5,μ=0.5,a2=2,d1=2,σ=0.5,d2=1,初始条件分别为:(x(0),y(0),z(0))=(2.5,2,1.5),(2,1.5,1),(1.5,1,0.5).

图3：x种群,y种群,z种群如图中所指.r=2,k=2.5,a1=3,m=1,μ=0.5,a2=2,d1=0.2,σ=0.75,d2=1,初始条件分别为:(x(0),y(0),z(0))=(2.5,2,1.5),(2,1.5,1),(1.5,1,0.5).

图3 图4

下面举例说明避难所对物种数量的影响,考虑系统

(11)

以下均取初始条件为：(x(0),y(0),z(0))=(1.5,1,0.5).

(1)当m=0时,系统(11)存在唯一稳定的正平衡点(0.8333,0.6667,0.5250),如图4实线.

(2)当m=0.5时,系统(11)存在唯一稳定的正平衡点(1.2390,0.6667,0.6031),如图4点线.

(3)当m=1时,系统(11)存在唯一稳定的正平衡点(1.4834,0.6667,0.5786),如图4星线.

图4：x种群,y种群,z种群如图中所指.m=0时用实线表示,m=0.5 时用点线表示,m=1.5时用星线表示,r=3,k=2.5,a1=3,μ=0.5,a2=2,d1=0.2,σ=0.75,d2=1,(x(0),y(0),z(0))=(1.5,1,0.5).

由图4可以看出保护力度适当的避难所可以促进猎物的生长且避难系数变化对x物种的数量影响较大,当避难系数增大时,x物种的数量增加. 对z物种的数量影响较小,对y物种的最终数量没有影响.