块体离散元颗粒模型细观参数标定方法及花岗岩细观演化模拟
2022-01-23王桂林王润秋
王桂林,王润秋, 孙 帆
(1.重庆大学 土木工程学院,重庆 400045; 2.库区环境地质灾害防治国家地方联合工程研究中心,重庆 400045)
1 研究背景
岩体破坏事实上是由岩体内部细观裂纹的闭合—产生—相互贯通连接而形成的宏观表现,因此研究微裂纹的行为特点,对于揭示岩体宏观行为特征是很有益处的[1-3]。大多数学者认为,岩体微裂纹的发展演化多由岩体矿物颗粒及其之间的胶结所控制[4-6]。自然界中的岩体颗粒多为几何形状复杂的矿物晶粒,并且晶粒与晶粒之间存在相应的胶结物质将其连接在一起,当岩体受到外荷载作用后,矿物晶粒便可能发生晶粒内部破坏的穿晶裂纹以及沿晶粒间胶结破坏的晶间裂纹[7-9],如图1所示。

图1 矿物的穿晶裂纹及晶间裂纹[9]Fig.1 Grain-boundary cracks and transgranularcracks[9]
研究岩体晶粒细观裂纹的发展,除了试验手段,人们越来越倾向于利用更加便利的数值模拟方法[10-11]。离散元法[12](Discrete Element Method, DEM)便是其中一种在研究岩体细观行为中较为常用的方法。目前以离散元法为主要计算核心的程序包括PFC2d& PFC3d、UDEC & 3DEC以及开源离散元程序Yade[13]、ESyS-Particle[14]和LIGGGHTS[15]。然而早期离散元模型却无法考虑矿物结构、晶粒破坏以及岩体中矿物颗粒不同属性,且模拟结果与实际情况也存在较明显的偏差。有的研究表明利用以颗粒流为代表的PFC程序等所得到的单轴抗拉强度与抗压强度之间的比值相对于实际岩体中的比值偏大[16-17],Cho等[17]还指出PFC的单轴抗拉强度标定后模拟所得的三轴抗压强度较低。除此之外,PFC中所标定的某些参数(摩擦系数、接触模量、平行键模量等)实际的物理意义不明确。为解决这些问题,Potyondy[18]最早提出PFC-GBM(Grain Based Model)这一概念并用于模拟刚性圆盘颗粒的行为,该方法可以用来模拟不同矿物的行为,但仍然存在以上PFC的缺点,同时对于具有多边形几何特征的矿物而言,无法准确描述其几何特征,因此建立以块体离散元(UDEC/3DEC)为主要核心的GBM便显示出其独特的优势。Voronoi tessellation是一种利用离散点来形成不规则多边形或多面体的方法,学者们常常将其与离散元相结合来模拟岩体的细观特征[19-24]。对于UDEC而言,利用Voronoi所生成的模型(GBM)是内置于程序中的,所生成的二维多边形无法考虑到实际矿物生长过程中晶粒取向以及解理等,因此三维块体离散元3DEC更适合用来利用GBM来解决早期离散元模型无法解决的问题。对此本文将利用Neper软件生成Voronoi模型,然后导入到3DEC中。
目前对于块体离散元 GBM的研究相对比较少,多停留在参数标定阶段,Wang等[25-26]以花岗岩为例分析了3种不同颗粒属性的参数标定过程,并利用块体离散元 GBM考虑了晶粒内和晶粒间的破坏模型。Ghazvinian等[27]研究了三维状态下圆柱形花岗岩的损伤等,同时提出了自己的标定方法。综合以前的研究,不难发现,大多文献所给出的标定程序多围绕弹性模量与泊松比,对于峰值强度的细观参数标定程序不足,同时承载板与试件之间的接触参数也少有考虑。基于此,本文将在前人研究基础之上,同时考虑承载板接触参数以及峰值强度,细化研究对象并提出相应的标定程序,之后利用改进的标定方法,标定不同矿物组分的花岗岩,进一步分析花岗岩中的穿晶裂纹以及晶界裂纹,并通过与室内试验结果对比,验证改进标定方法后的块体离散元 GBM方法在岩体细观演化中的准确性。
2 GBM岩样宏细观参数分析
2.1 块体离散元 GBM岩样
模型采用板状试件,宽高为50 mm×100 mm,厚度为1 mm,晶粒随机生成,晶粒平均尺寸为3 mm,一共900个晶粒,如图2(a)所示。模型上下两侧为加载钢板,板厚0.05 mm,加载钢板垂直方向两侧均施加垂直方向的速度约束,模型XZ平面均进行Y方向的位移约束,使之成为平面应变问题。单轴压缩试验中控制加载速度为0.1 m/s,直拉试验中控制加载的速度为0.01 m/s。值得注意的是无论是单轴压缩试验还是直拉试验模型均采用伺服控制,同时在模型内部设较大局部阻尼值(0.90)以保证在整个试验的过程中岩体均为准静态过程,从而实现准静态加载。加载过程中监测其横向应变、轴向应变以及轴向应力。已有文献研究表明当应力监测区域增大时,监测区域大小的影响将会消失[27]。因此,横向应变的监测点位于试样左右两侧距试件边缘0.01 m处,轴向应变的监测点位于两侧压板接触面0.02 m,轴向应力为横向及轴向应变监测点所包围区域的平均值σzz,如图2(b)所示。
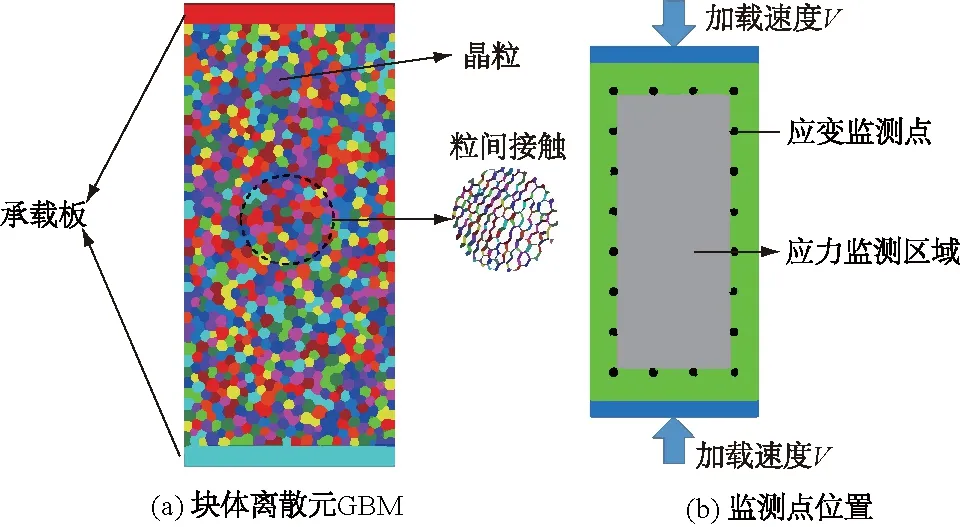
图2 块体离散元GBM和监测点位置Fig.2 Block discrete element GBM and the position ofmonitoring points
模型的力学特征受到材料本身属性的影响,为减少计算时间,本文将晶粒设为弹性,同时粒间采用库伦滑移准则,晶粒与承载板之间采用接触摩擦滑移,参考已有的研究经验[25-27],表1、表2及表3分别给出了上述3种属性参数值。值得注意的是接触属性里残余抗拉强度以及残余黏聚力设置为0[28-29]。

表1 承载板及晶粒参数Table 1 Bearing plate and grain parameters

表2 承载板与晶粒之间的接触参数Table 2 Contact parameters between bearing plateand grains
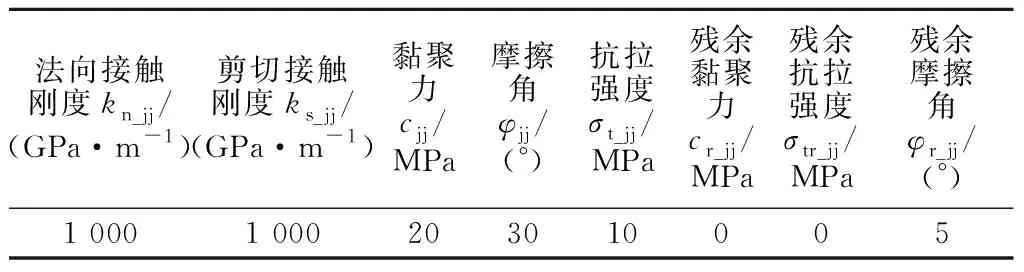
表3 晶粒之间的初始接触参数Table 3 Initial contact parameters between grains
2.2 单轴压缩下粒间接触属性的影响
2.2.1 承载板接触参数的影响
承载板的接触参数主要包括承载板与晶粒之间的切向接触刚度ks_bj、法向接触刚度kn_bj以及摩擦角φbj。图3为单因素下不同接触刚度及摩擦角的数值模拟试验结果,其中图3中的(a)、(c)、(e)为承载板接触参数对试样的弹性模量E及泊松比ν的影响,图3中的(b)、(d)、(f)为承载板接触参数对试样的峰值强度σf的影响。由图3中的(a)、(c)、(e)可知:改变ks_bj时,试样的弹性模量基本不发生变化,泊松比将会随其增大而逐渐减小,但总体减小的量并不大;改变kn_bj对弹性模量及泊松比基本没有影响;改变摩擦角,弹性模量基本不发生变化,但泊松比先减小后增大,并在60°左右达到最小值。由图3中的(b)、(d)、(f)可知,总体来说试样的峰值强度受承载板与晶粒间接触属性的影响相对较小,偶有起伏,但最大值与最小值之间的差距不大。综合试验结果可以发现在本试验条件下,承载板接触参数对于试验结果的干扰相对较小,因此保证了数值试验所采取的监测手段以及所记录的数据结果的可靠性。
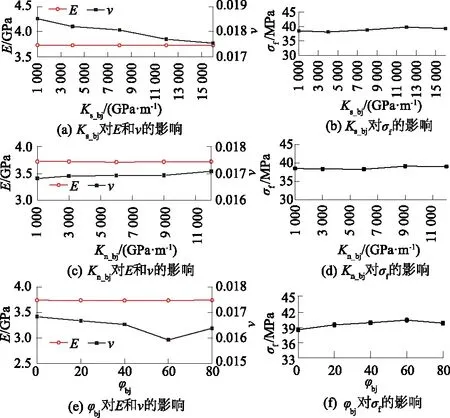
图3 承载板与晶粒之间接触参数对试样力学参数的影响Fig.3 Influence of contact parameters between bearingplate and grains on mechanical parameters of specimen
2.2.2 粒间接触刚度的影响
研究表明[25-27],粒间接触刚度将会影响试样的弹性模量E以及泊松比ν,但很少人给出粒间接触刚度对峰值强度σf的影响,同时大部分的文献仅仅给出粒间法向接触刚度kn_jj不变的情况下粒间接触刚度比值对弹性模量及泊松比的影响,而忽略了粒间剪切刚度ks_jj不变时粒间刚度比的影响。图4(a)为保持粒间剪切刚度ks_jj为1 000 GPa/m,粒间刚度比对试样的弹性模量及泊松比的影响,图4(b)则为其对峰值强度的影响。增大粒间刚度比,试样的泊松比、弹性模量以及峰值强度均随之而增大。然而相对于图5(a)而言,当保持粒间kn_jj为20 000 GPa/m时,弹性模量却随粒间刚度比的增大而减小,泊松比则与图4(a)有相同的趋势,同时对比图4(b)与图5(b)中的峰值强度,图5(b)中的峰值呈现先增大后减小的趋势,达到最大值时所对应的粒间接触刚度比值为5左右。保持粒间接触刚度比值不变,增大粒间法向接触刚度,弹性模量、泊松比以及峰值强度均会随之单调增加,如图6(a)、图6(b)所示。
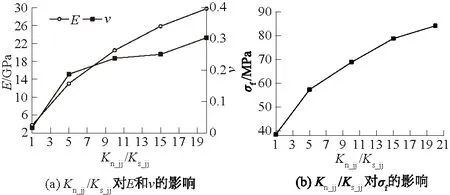
图4 ks_jj=1 000 GPa/m时粒间刚度比对试样力学参数的影响Fig.4 Influence of ratio of stiffness between grains on themechanical parameters of specimens(ks_jj=1 000 GPa/m)
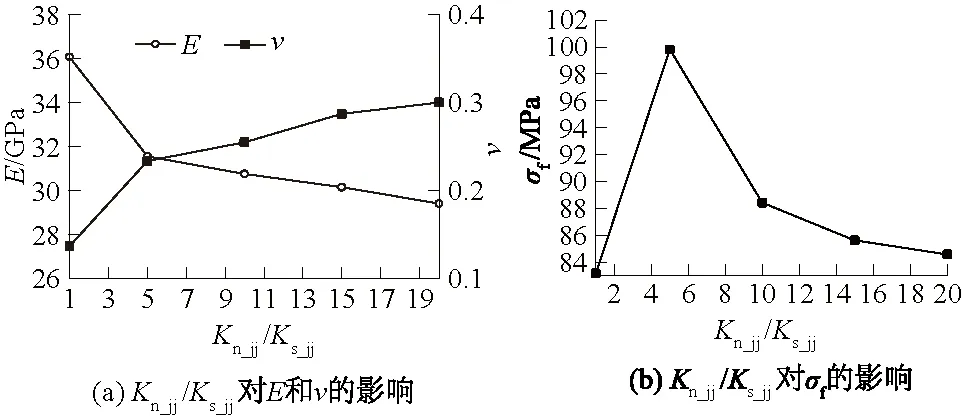
图5 kn_jj=20 000 GPa/m时粒间刚度比对试样力学参数的影响Fig.5 Influence of ratio of stiffness between grains on themechanical parameters of specimens(kn_jj=20 000 GPa/m)
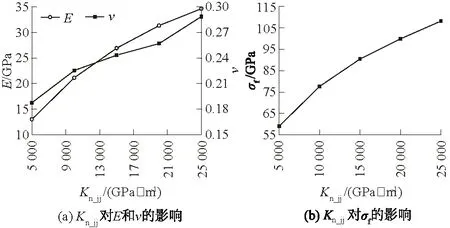
图6 kn_jj/ks_jj=5时粒间刚度比对试样力学参数的影响Fig.6 Influence of ratio of stiffness between grains onthe mechanical parameters of specimens (kn_jj/ks_jj=5)
综合以上分析,试样的弹性模量、峰值强度以及泊松比中,仅泊松比随粒间接触刚度的变化呈现单调性,因此在标定粒间接触刚度时,首先应考虑泊松比。通过计算图4(a)、图5(a)、图6(a)中泊松比的平均差可以发现,当保持粒间接触刚度比值不变时,其平均差(0.027)相对于保持粒间法向接触刚度不变时的平均差(0.046)以及粒间剪切刚度不变时的平均差(0.079)最小,其离散性较小,能够保证在标定过程中泊松比仅在小范围内变化。故在调整粒间接触刚度时应先观察初始计算后的弹性模量及泊松比,若两者均大于或小于试验值,先保持粒间接触剪切刚度不变,然后调节粒间接触法向接触刚度,如图4(a)所示,反之保持粒间法向接触刚度不变,调整粒间剪切刚度,如图5(a)所示。由此标定泊松比的细观参数同时使弹性模量趋近于实际值,之后再保持粒间刚度比,调整粒间法向接触刚度,使得模量快速到达实际值。
2.2.3 粒间摩擦角、黏聚力、抗拉强度的影响
图7、图8、图9分别为粒间摩擦角φjj、黏聚力cjj以及抗拉强度σt_jj对试样的力学参数弹性模量E、泊松比ν以及峰值强度σf的影响。
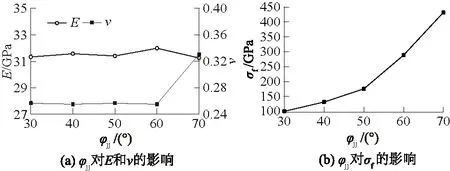
图7 粒间摩擦角对试样力学参数的影响Fig.7 Influence of contact friction angle betweengrains on mechanical parameters of specimen
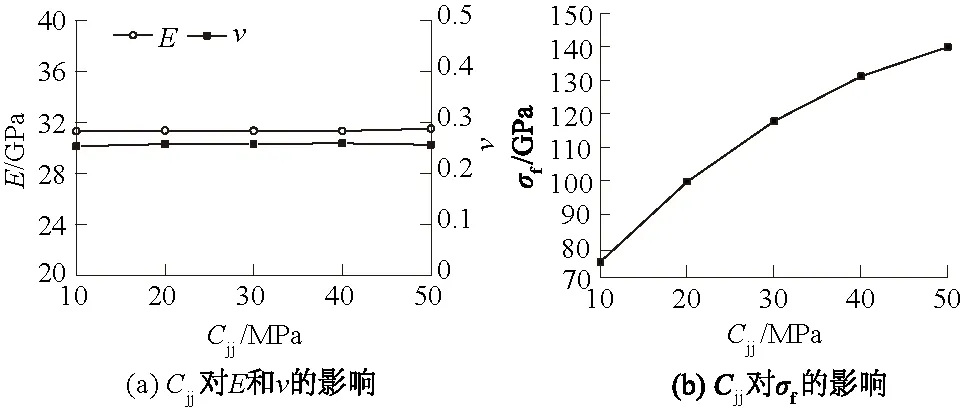
图8 粒间黏聚力对试样力学参数的影响Fig.8 Influence of contact cohesion between grains onmechanical parameters of specimen
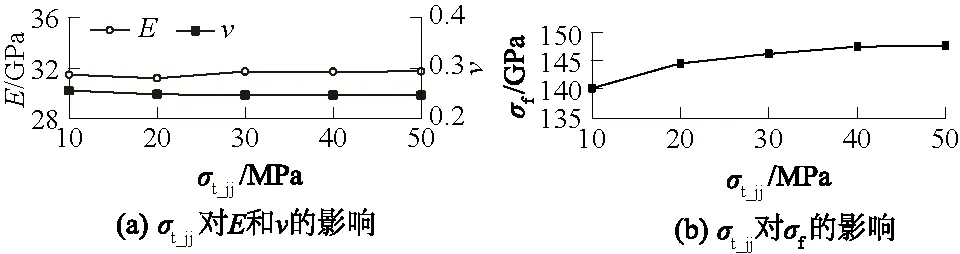
图9 粒间抗拉强度对试样力学参数的影响Fig.9 Influence of contact tensile strength betweengrains on mechanical parameters of specimen
由图7(a)、图8(a)、图9(a)可知,粒间摩擦角、黏聚力以及抗拉强度对试样的弹性模量、泊松比影响相对较小,弹性模量基本维持在31.3 GPa左右,而泊松比则基本维持在0.25。由图7(b)、图8(b)、图9(b)可知,粒间摩擦角、黏聚力以及抗拉强度对试样的峰值强度的影响中,粒间摩擦角的影响最为显著,如图7(b)所示;粒间黏聚力对峰值强度的影响次之,趋势与粒间摩擦角的影响一样,如图8(b)所示;粒间抗拉强度对峰值强度的影响最小,随着粒间抗拉强度的增加,试样的峰值强度增加缓慢,如图9(b)所示。根据以上分析结果,适宜用粒间摩擦角、黏聚力及抗拉强度来标定峰值强度,其平均差分别为107.88、20.09、3.33 MPa,因此数值试验所得的峰值强度过高或者过低时,可采用略微减小或增大粒间摩擦角的做法,因为这样可以快速改变峰值强度,之后再改变粒间黏聚力以及粒间抗拉强度使之趋于实际值。值得注意的是在调整粒间摩擦角时应选择较小值,因为当粒间摩擦角的值增大到一定程度时(>60°)泊松比会产生突变,如图7(a)所示。
2.3 抗拉强度细观参数的标定
本文利用直拉试验进行抗拉强度细观参数的标定,所采用的模型和压缩试验保持一致,为保证拉伸时试样与承载板之间不发生分离,初始时承载板和晶粒之间的接触属性改用摩尔库伦滑移,并将黏聚力设置为较大值。试验结果表明试样的抗拉强度(σt)主要受晶粒间黏聚力Cjj及粒间抗拉强度σt_jj影响,图10给出了这种影响对试样整体抗拉强度的作用效果。由图10(a)可以看出,晶粒间黏聚力对试样抗拉强度的影响较弱,抗拉强度基本不随着粒间黏聚力的大小发生太大的变化,极差仅为0.328 MPa。试样的抗拉强度对于粒间抗拉强度的变化最为敏感,如图10(b)所示,当粒间的抗拉强度增大时,试样的抗拉强度也急剧增加,但始终小于粒间抗拉强度,其值大小约为粒间抗拉强度的一半。因此在校准抗拉强度时,改变粒间抗拉强度是最合理的。
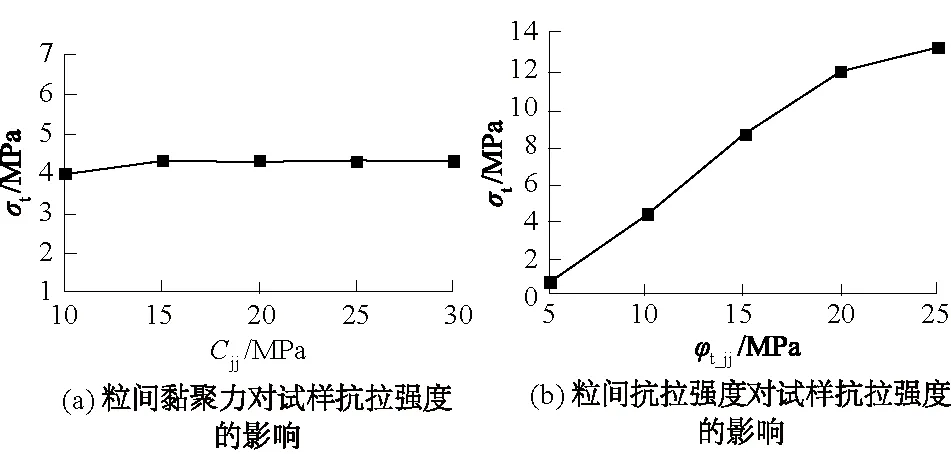
图10 粒间黏聚力和粒间抗拉强度对试样抗拉强度的影响Fig.10 Influence of contact cohesion and contacttensile strength between grains on tensile strengthof specimen
3 单轴拉压下块体离散元GBM参数标定方法
综合以上单轴压缩试验以及直拉试验,以实验室所得的岩体弹性模量、泊松比、峰值强度以及抗拉强度为参照对象,对块体离散元 GBM数值模拟方法中的细观参数进行标定,根据上述获得的影响规律,其标定方法如图11所示。
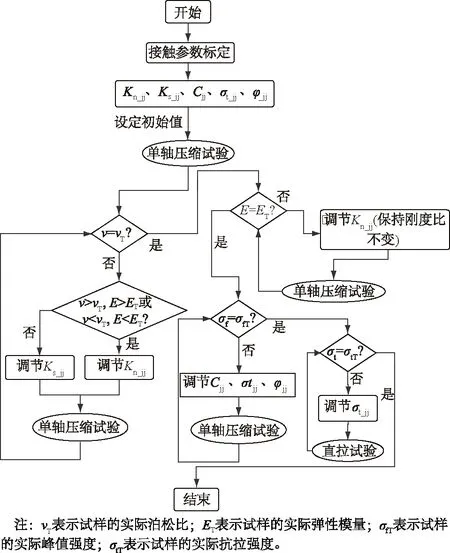
图11 块体离散元GBM标定方法Fig.11 Discrete element GBM calibration method
标定方法说明:模型标定时首先应考虑初始计算结果中的泊松比和弹性模量与实际泊松比和弹性模量之间的大小关系,改变粒间接触刚度以校准泊松比同时使得弹性模量快速趋于实际值,减少标定时间。然后,保持泊松比不变,调节法向接触刚度以使弹性模量符合实际弹性模量,之后保持接触刚度不变,按照此时的峰值强度大小调节粒间黏聚力以及粒间摩擦角以调整峰值强度达到实际值,最后通过直拉试验调节粒间接触抗拉强度以匹配总体的抗拉强度。
4 算例验证
4.1 花岗岩块体离散元GBM
花岗岩主要由长石、石英、黑云母等矿物组成。在建立数值模型时,目前已有的数值方法多将其考虑为同一种均质的矿物,并将不同参数进行平均处理;部分学者利用其他GBM方法尽管考虑到了矿物的差异性,但忽略了实际矿物生长过程中解理的影响。因此为了使本文采用的块体离散元GBM更加贴合实际,模型中的矿物作以下处理:
(1)长石具有2组相互垂直或接近垂直的相交解理,发生破坏时其裂纹一般沿着解理[30],为简化计算,数值采用平面应变模型,因此仅考虑其中的一组解理。
(2)石英完全无解理,受力破坏时毫无规则,如果没有预先存在裂纹则很难破坏[30],故在计算之前先将其矿物晶粒预制为6个不均等的微晶粒。
(3)黑云母完全解理,但是当晶间或穿晶裂纹发展到黑云母时,其裂纹扩展大多沿云母片之间的夹层,形成穿晶裂纹的情况较为少见[31],在平面应变模型下考虑为片状黑云母,不发生破坏。
基于此,为了实现晶粒本身的破坏,本文根据每一种矿物的解理性质对每一个晶粒进行再次切割,预制成含解理的矿物,如图12所示。本文所采用的花岗岩成分如表4所示[32],由于绿泥石和方解石的含量较低,对整个模型的影响较小,因此为简化模型未考虑这2种矿物,并将其占比分配给长石,数值模型采用调整后的花岗岩成分,如表5所示。
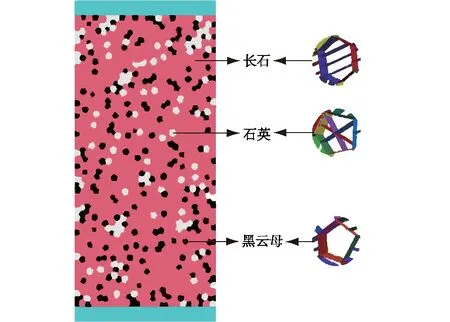
图12 花岗岩数值模型Fig.12 Numerical model of granite

表4 花岗岩矿物组成比例[32]Table 4 Components and individual proportionof granite[32]

表5 模型中的花岗岩矿物组成Table 5 Modified components and individual proportionof granite
根据以上结果建立的块体离散元GBM如图12所示。利用上述标定方法对模型的参数进行标定,试验弹性模量为31 GPa[32],标定后的弹性模量为29.8 GPa,两者差距不大,而最终获得的接触参数如表6所示。值得注意的是若要得到晶粒内的接触参数和晶界中的接触参数是很复杂的,因此为减少计算量,数值模型晶粒间解理的参数和晶界间的参数采用同一组参数。
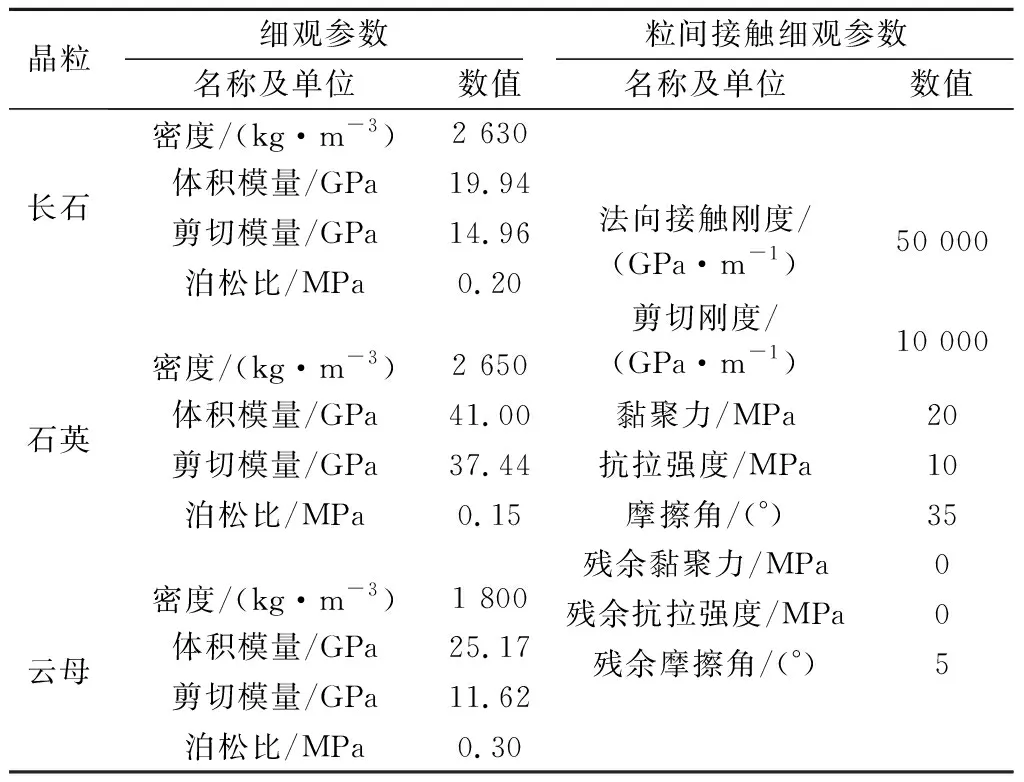
表6 晶粒及粒间接触的细观参数Table 6 Mesoscopic parameters of grain and contact
4.2 花岗岩晶界裂纹及穿晶裂纹分析验证
利用自编的fish程序,统计单轴压缩下花岗岩晶界裂纹(晶体与晶体之间的已破坏的接触)以及晶内裂纹(晶粒内部破坏的接触)累计统计曲线如图13所示。
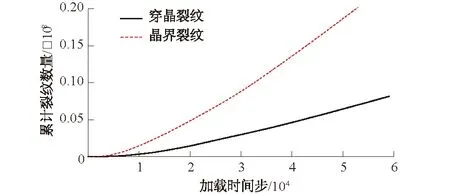
图13 花岗岩穿晶裂纹及晶界裂纹统计Fig.13 Statistics of granite’s transgranular cracksand grain boundary cracks
由图13可知,在早期的加载阶段晶界裂纹与穿晶裂纹均未出现,随着加载的进行晶界裂纹与穿晶裂纹的数量均开始增加,并且其增量逐渐增大,但是晶界裂纹的数量始终多于穿晶裂纹的数量,这与室内试验的结论相似[33]。
4.3 不同矿物之间晶界裂纹分析验证
Ghasemi等[34]经过大量的细观试验指出,长石的弹性模量小于石英的弹性模量,因此石英-黑云母晶界裂纹数目大于长石-黑云母晶界裂纹数目,如图14所示。然而针对类似的这种现象,大多仍停留在细观试验上,试验过程复杂且难以掌控。为解决这一难题,室内数值模拟便成了一种良好的手段,但是目前已有的数值方法少有考虑晶界裂纹,更不用说不同种矿物之间的晶界裂纹。基于此,本文利用GBM模拟不同矿物晶界面细观裂纹开展行为。由于试样中矿物的含量不一样,为保证试验结果的准确性,其他条件保持不变,将长石和石英的含量调换,并在同样的情景下加载,统计结果仅考虑其裂纹的数目,忽略峰值以及弹性模量的影响,得到如图15所示的石英-黑云母与长石-黑云母累计晶界裂纹之差的统计曲线。
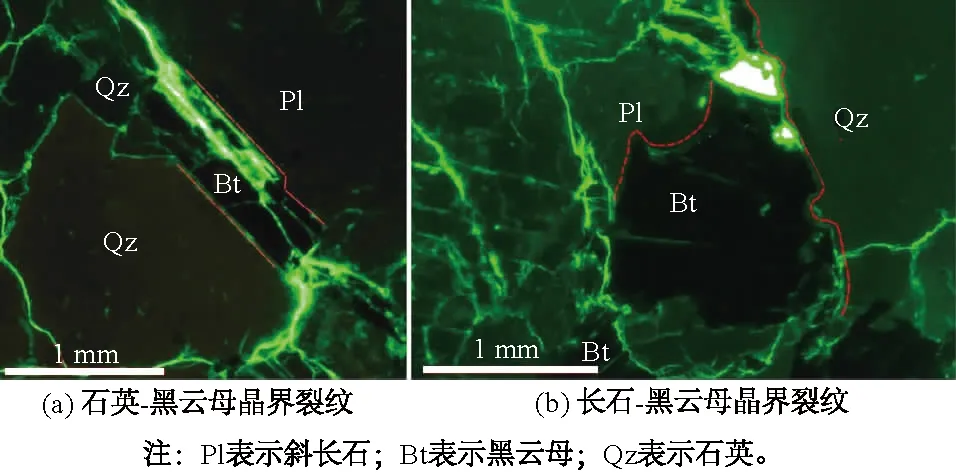
图14 石英-黑云母晶界裂纹及长石-黑云母晶界裂纹[34]Fig.14 Quartz-biotite grain-boundary cracks andfeldspar-biotite grain-boundary cracks[34]
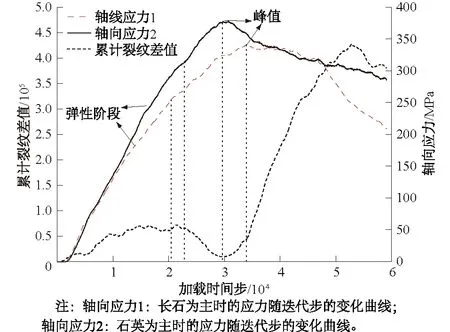
图15 石英-黑云母与长石-黑云母之间的差值Fig.15 Difference between quartz-biotite andfeldspar-biotite
同样的加载条件下,花岗岩单轴压缩下矿物晶界的破碎和矿物的弹性模量息息相关,如图15所示:弹性阶段,两者之间的差值逐渐增加,但增加的程度较小,此阶段石英的弹性模量较大,抵抗变形的能力较大,黑云母的弹性模量小,抵抗变形的能力较小,两者在晶界处容易产生晶界裂纹,而长石的弹性模量较小,可以与黑云母一起变形,故在晶界处产生的晶界裂纹较少,但总的来说两者之间的差值不大;弹塑性阶段,两者之间的差值出现下降,长石-黑云母之间晶界裂纹的增长量大于石英-黑云母长石之间的晶界裂纹,其原因在于当长石的含量占花岗岩主要成分时,花岗岩的总体弹性模量小于石英占主要成分时,花岗岩容易进入塑性,裂纹增加明显,因此出现下降段;峰后花岗岩破坏阶段,石英占主要成分时,最先达到峰值强度,石英-黑云母由于能量的突然释放晶界裂纹呈现爆发式的增长,其值远大于长石-黑云母之间的晶界裂纹,此时长石占主要成分的花岗岩还未达到峰值,两者之间的差值增量逐渐增大,直到后者达到峰值,差值开始稳定增长,达到差值峰值之后两者之间的裂纹差逐渐减小。总的来说两者之间的差值在整个加载计算过程中均>0,因此可以证明花岗岩单轴压缩下石英-黑云母之间的晶界裂纹大于长石-黑云母之间的晶界裂纹,这与实际的室内细观试验结果一致[34]。
5 结 论
(1)岩体单轴压缩试验以及直拉试验3DEC-GBM数值模拟结果表明,岩体弹性模量以及泊松比的细观参数标定主要取决于晶粒间的接触刚度,岩体峰值强度主要与粒间黏聚力、抗拉强度以及摩擦角的有关,而岩体的抗拉强度受晶粒间抗拉强度的影响最为显著。
(2)花岗岩单轴压缩过程中在矿物内部以及晶界处均会产生细观裂纹。经与试验结果对比,呈现的规律基本一致,花岗岩内晶界裂纹的数量明显大于穿晶裂纹的数量。同时其晶界裂纹受矿物的弹性模量影响较大,长石的弹性模量小于石英的弹性模量,因此在加载的过程,其与黑云母之间的晶界裂纹数小于石英与黑云母之间的晶界裂纹数,并且两者之间的差值大小与加载过程中花岗岩内部的应力状态有关。
(3)由于标定过程中未考虑不同矿物之间的接触以及矿物内部的接触,也未考虑圆柱体等试件,因此,推广本文方法时需要对这些因素进一步研究。
