一种行星齿轮裂纹深度评估新特征及其应用
2022-01-23吴守军冯辅周吴春志贾子永
吴守军, 冯辅周, 吴春志, 贾子永
(1. 中国人民解放军 63963部队,北京 100072;2.陆军装甲兵学院 车辆工程系,北京 100072;3. 航天工程大学士官学校,北京 102200; 4. 中国人民解放军 32184部队,北京 100093)
某型坦克行星变速箱由于工作环境恶劣,齿轮极易出现裂纹等故障,对裂纹损伤程度进行评估是开展装备视情维修的前提. 损伤程度评估需要大量的故障演化数据,目前,基于故障模拟实验数据开展损伤程度评估的方法应用较为广泛.
张星辉等[1]利用K均值聚类算法对退化状态数目进行优化,将齿轮退化过程分为3个阶段,分别选择3个阶段数据的特征矩阵训练分类器,利用观测值落在3个分类器的概率实现退化状态定位;仝蕊等[2]将局部特征尺度分解、贝叶斯信息准则与复合谱分析结合计算复合谱熵,构建齿轮退化特征向量,对齿轮全寿命数据进行退化状态识别;倪祥龙等[3]利用均方根替换峭度,提出RMS谱、RMS归一化谱等退化特征,通过分析单级行星齿轮全寿命实验数据,针对不同的退化工况,选择不同频带信号的RMS趋势进行状态评估;WANG等[4]利用齿轮角加速度信号的时域特征训练隐马尔科夫模型,提出健康因子用于齿轮退化性能评估;PAN等[5]将噪声自适应的完全集成经验模态分解与核主成分分析结合实现信号降噪和信息融合,提出了健康因子实现行星齿轮箱退化状态评估;ROMERO等[6]对风电机组行星齿轮振动信号进行本征尺度分解,利用分量包络谱提取故障频率,实现齿轮退化状态评估与故障预警;KUNDU等[7]利用残留振动信号与健康状态信号的相关系数对齿轮点蚀故障程度进行评估;PATTABIRAMAN等[8]提出了边频带能量比指标,对风电机组行星齿轮箱故障程度进行评估.
基于实验故障数据进行齿轮状态评估的缺点是实验成本高、周期长、成功率低,实验数据背景噪声大,故障演化信息微弱,不利于故障演化规律研究. 行星轮系集中参数动力学模型具有建模简单、计算效率高、故障程度易于设置等诸多优点,且模型的仿真响应没有噪声干扰,故障演化信息特征明显,易于观察故障演化规律. 程哲等[9]建立了行星轮系纯扭转集中参数模型,并获得不同程度太阳轮裂纹、点蚀[10]、胶合损伤[11]、缺齿[12]的仿真信号,提取峭度、FM0等损伤特征,结合关联度分析理论构建标准损伤模式,计算未知损伤模式与标准损伤模式的关联度,实现损伤程度评估. 由此可见,基于行星轮系动力学模型开展损伤程度评估具有可行性. 但程哲等所建模型为纯扭转模型,采用方波法估算的啮合刚度,没有考虑啮合阻尼等因素,因此模型尚需进一步完善.
文中以行星变速箱第3级行星轮系(K3排)为研究对象,利用势能法计算啮合刚度,考虑平移自由度、啮合阻尼等因素,建立K3排平移-扭转动力学模型,将不同深度裂纹的啮合刚度代入微分方程获取仿真故障响应,根据仿真信号频谱特点提取特征,最后通过不同程度裂纹的实验数据验证特征的有效性.
1 行星轮系动力学仿真
1.1 平移-扭转模型建立
行星变速箱K3排行星轮系实物与结构示意图如图1所示,由太阳轮、6个行星轮、齿圈和行星架组成,其中太阳轮固定,齿圈为输入构件,行星架为输出构件. 行星齿轮的模数为5 mm,压力角为20°,杨氏模量为206 GPa,泊松比为0.3,其他参数如表1所示.

图1 K3排实物与行星轮布局

表1 K3排齿轮参数


图2 K3排平移-扭转动力学模型
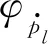
K3排运动微分方程矩阵形式如下:

(Km+Kb)Q(t)=T
(1)
式中:M为质量矩阵;Cm为啮合阻尼矩阵;Cb为支撑阻尼矩阵;Km为啮合刚度矩阵;Kb为支撑刚度矩阵;Q为位移矩阵;T为负载矩阵.
1.2 啮合刚度求解与仿真分析
齿轮出现裂纹时,其啮合刚度会降低,势能法计算啮合刚度具有效率高、考虑的因素全面等优点. LIANG等[14]考虑了齿根圆与基圆之间圆角部分对啮合刚度的贡献,完善了齿轮啮合刚度计算模型,并提出了裂纹齿轮计算模型,文中采用此模型计算含裂纹齿轮的啮合刚度.
以太阳轮齿根裂纹为例,设置10个等级的裂纹程度:10%、20%、…、90%、100%. 研究不同深度裂纹时,太阳轮-行星轮啮合刚度如图3所示. 在一个啮合周期内,单双齿交替时啮合刚度出现跃变,随着裂纹程度的增加,啮合刚度逐渐降低,当裂纹达到100%时,单齿啮合刚度降为0.

图3 不同深度裂纹时太阳轮-行星轮啮合刚度
利用函数ode15s求解行星轮系运动微分方程,相对误差取10-6,绝对误差取默认值10-6,每个啮合周期采样点取50,输入转速为60 r/min,啮合频率fm为21.18 Hz,太阳轮故障频率fs=2.12 Hz,仿真步长为1/50/21.18=9.44×10-4s,采样率为1 060 Hz,仿真时间为行星架周期Tc(1.416 s). 得到不同深度裂纹的行星轮系响应如图4所示. 限于篇幅,仅列举齿轮正常、裂纹30%、50%、70%、90%的仿真信号.

图4 不同深度裂纹的行星轮系仿真信号
2 裂纹程度评估特征提取
2.1 特征提取
由图4可知,随着裂纹深度的增加,故障频率及其倍频、故障边频带逐渐增多,且幅值越来越大,尤其是裂纹深度超过50%之后,故障频带幅值显著增加. 同时,啮合频率及其倍频幅值也随着裂纹深度的扩展而增加,因此,以故障频带的幅值与啮合频率幅值为切入点,提取裂纹深度评估特征. 为了避免量纲的干扰,特征中应包含故障频带幅值与啮合频率幅值之比. 由于齿轮制造和安装误差,齿轮正常状态的实测振动信号中也会含有故障频率成分,采用故障频带的多倍频幅值累积量可以有效降低误差的影响. 因此,文中提出两个损伤程度评估特征.
① 故障频率及多倍频幅值累积量与啮合频率幅值之比(the ratio of cumulative amplitude of multiple fault frequency to amplitude of meshing frequency, RCMFAM),计算公式为
(2)
式中:X(fm)为啮合频率幅值;X(kfs)为故障频率及其倍频幅值;Nb为选取的故障频率最大倍频数,由于啮合频率是故障频率的10倍,只需取前5倍故障频率即可,即Nb=5.
② 寻找频谱中幅值最大的啮合频率倍频,由仿真信号频谱可知,幅值最大的啮合频率为16fm,计算其两边的故障边频带幅值累计量,提出特征:多级故障边频带幅值累积量与啮合频率倍频中最大幅值之比(the ratio of cumulative amplitude of multi-stage fault sideband to maximum amplitude of multiple meshing frequency, RCMFSM),计算式为
RCMFSM=
(3)
式中:X(nfm)为啮合频率倍频的幅值;X(nfm±kfs)为多级故障边频带幅值;Ns为选取的故障边频带最大阶数,由于啮合频率是故障频率的10倍,只需取前5阶边频带,即Ns=5.
2.2 特征关联性与一致性评价
为了验证所提特征的有效性和优势,选出最佳特征评估裂纹深度,将所提特征与传统的时域、频域特征比较. ①常规时域特征(F1~F10):峰峰值、标准差、偏态、峭度、均方根、波峰因子、脉冲因子、波形因子、均方根差、能量算子[15];②高阶时域特征(F11~F20):NA4、NA4*、FM4、FM4*、M6A、M6A*、M8A、M8A*、NB4、NB4*[16];③频域特征(F21~F29):平均频率、频率中心、频率均方根、频率标准差、FM0、边频带指数、边频带等级因子[17]、边带主频幅值比、残差信号频谱NA4[18];文中所提特征记为F30、F31.
故障程度评估特征需具有对齿轮损伤演化过程进行跟踪的能力. 损伤程度量化评估特征最重要的特性是关联性,即特征值与损伤程度之间单调相关,且能区分不同程度损伤的能力.
计算太阳轮不同深度裂纹仿真信号的时域、频域特征值,观察特征值随着裂纹深度增加的变化趋势. 由于各个特征的量纲不一致,为了对比分析各个特征的变化趋势,需要进行幅值归一化,得到10个常规时域特征归一化幅值如图5所示. 由图可知,随着裂纹程度增加单调增加的特征为:F1、F2、F5,因此这3个特征满足关联性要求.
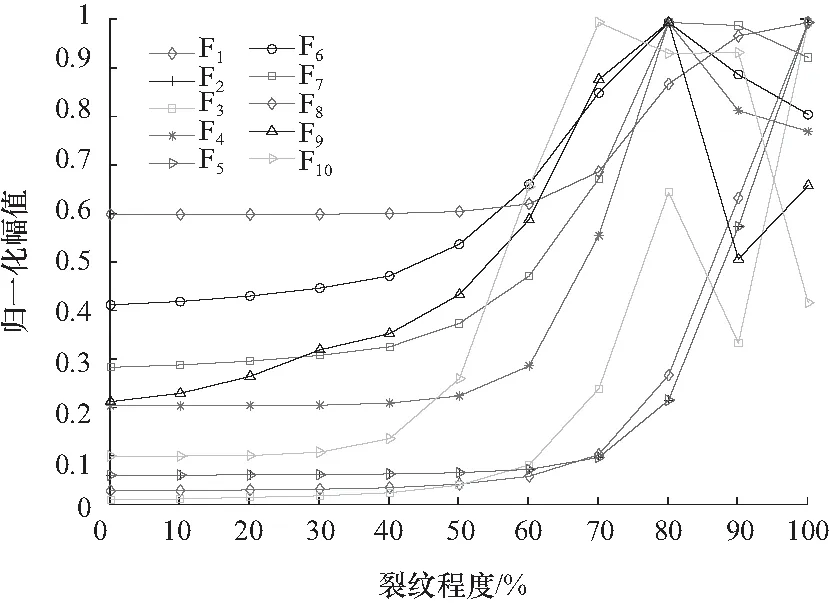
图5 常规时域特征归一化幅值
10个高阶时域特征归一化值随裂纹深度的变化趋势如图6所示. 由图可知,F11在裂纹20%之前单调减,后面随着裂纹深度的增加几乎不变,因此不适于跟踪裂纹演化过程;特征F13、F15、F17、F19随裂纹深度增加不是单调变化的,也不符合关联性要求;F12、F14、F16、F18、F20虽然在裂纹80%之后单调增加,但在裂纹80%之前几乎一直为0,无法反映裂纹演化前期的变化规律,也不符合规律,综上可知,高阶时域特征均不符合关联性要求.

图6 高阶时域特征归一化幅值
11个频域特征归一化值随裂纹深度的变化趋势如图7所示. 由图可知,特征F21、F26、F28、F30、F31随着裂纹深度增加单调递增,满足关联性要求;其余特征均不单调变化,不满足关联性要求.

图7 频域特征归一化幅值
综上,初步筛选出满足关联性要求的特征为F1、F2、F5、F21、F26、F28、F30、F31. 通过特征值与损伤度阶跃曲线(step curve of damage degree, SCD)的一致性程度评价,筛选出与损伤度阶跃曲线一致性最高的特征,用于行星齿轮裂纹深度评估. 将特征值范围分为10个等级,分别对应10个损伤程度,所选关联性特征归一化幅值与损伤度阶跃曲线如图8所示.
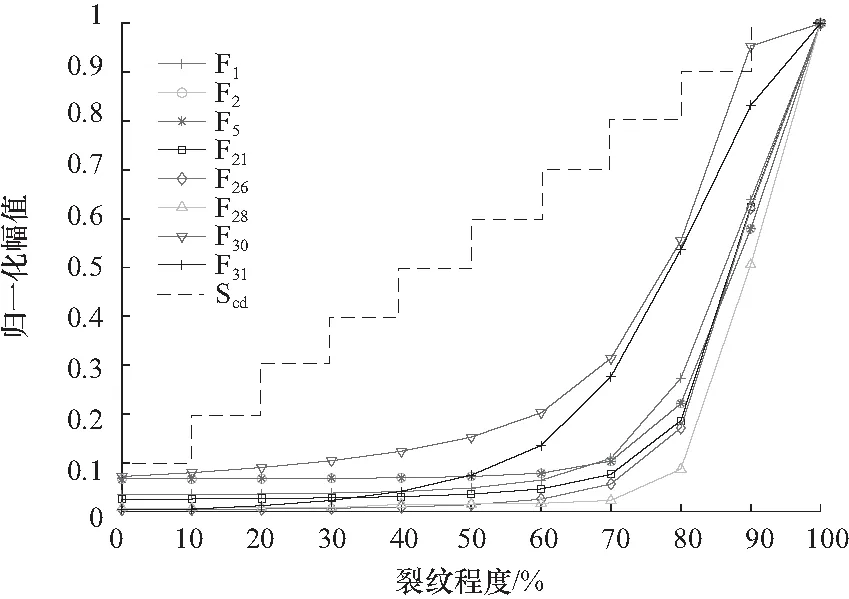
图8 关联性特征的归一化幅值
利用双样本Z值一致性检验特征对齿轮裂纹演化过程的跟踪能力,Z值越小,说明两样本的一致性越好,当Z值为0时,表示两曲线完全重合.
(4)
关联性特征的归一化幅值与损伤度阶跃曲线的双样本Z值如图9所示. 由图可知,将特征按照Z值从小到大排序,所提特征F30、F31分别位于第1、第2,其中特征F30的归一化幅值随裂纹深度的变化趋势与裂纹发展的各个阶段较为吻合,因此选择F30评估齿根裂纹深度.

图9 关联性特征的双样本Z值
3 行星变速箱实验验证
3.1 实验数据采集与预处理
在太阳轮齿根处受拉力侧通过线切割注入裂纹,裂纹深度为5 mm(50%),裂纹宽度为齿宽,裂纹演化方向基本垂直于齿面. 以断齿故障实验信号为基准进行幅值归一化,太阳轮正常(裂纹0%)、裂纹深度50%和断齿(裂纹深度100%)故障件如图10所示.

图10 太阳轮故障件
行星变速箱故障模拟实验台如图11所示,主要由行星变速箱、电机、液压站、数据采集仪和控制台等组成. 挡位为Ⅳ挡,输入转速为600 r/min,负载为300 N·m,振动测点位于K3行星排上方,采集齿轮正常、50%裂纹和断齿三种状态的振动数据,采样率Fs为20 kHz,采集三组,每组采样时间为30 s.

图11 行星变速箱故障模拟实验台
行星变速箱实验信号不仅包含K3排的啮合频率和太阳轮故障及其倍频,还存在定轴轮系、主泵、回油泵的啮合频率及其倍频,特征值计算之前需要进行预处理,将无关的频率成分滤掉. 采用频谱编辑方法将上述常规啮合频率滤除. 输入转速600 r/min时,各个频率成分如表2所示.

表2 行星变速箱各部分频率
将每种状态数据分为10组,每组数据长度取100 000点. 太阳轮断齿实验振动信号如图12所示. 由频谱低频段可以观察到上述啮合频率和太阳轮故障频率,但太阳轮故障频率幅值较低,且倍频成分被掩盖,难以提取.
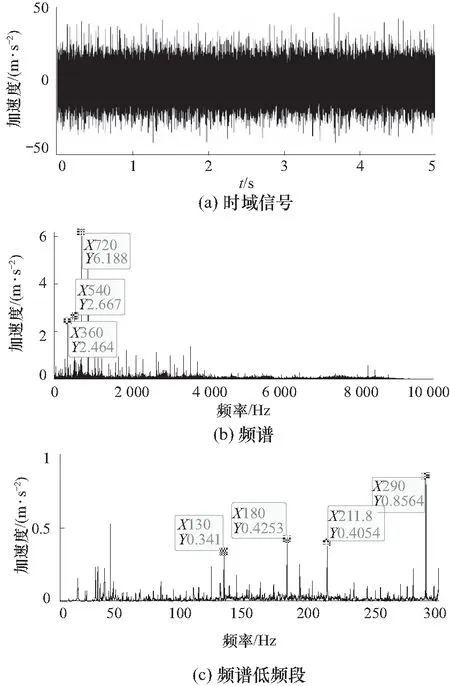
图12 滤波前的断齿信号
采用频谱编辑滤波后得到的振动信号如图13所示. 由于傅里叶变换得到的频谱关于Fs/2对称,频谱编辑中傅里叶逆变换时只取前一半的点,因此滤波后的残差信号长度为50 000点. 滤波后信号的幅值明显减小,频谱中可以明显观察到太阳轮故障频率及其倍频.

图13 滤波后的断齿信号
3.2 裂纹深度评估
利用滤波后信号计算RCMFAM特征值,得到归一化特征值、裂纹深度与样本数绘制在三维坐标系中,得到损伤程度评估如图14所示.

图14 损伤程度评估结果
由图可知,三种状态数据的特征归一化平均值与特征仿真曲线交点在裂纹深度坐标上的投影分别为2.28%、51.95%、100%,实际裂纹尺寸分别为0、50%、100%,正常状态信号得到的裂纹深度评估结果不为0,可能是齿轮制造误差引起啮合刚度差异造成的,可见评估结果基本一致,验证了所提特征的有效性.
4 结 论
基于行星轮系平移-扭转动力学模型仿真了太阳轮不同深度裂纹的动力学响应,根据仿真信号频谱中故障频率及倍频幅值和啮合频率幅值变化规律,提出了裂纹深度评估特征RCMFAM、RCMFSM,通过关联性和一致性评价准则对所提特征和传统特征进行评价,最终筛选RCMFAM作为裂纹深度评估特征,该特征与裂纹深度具有较强的关联性,与裂纹损伤度阶跃曲线的一致性最强;利用RCMFAM特征对齿轮正常、太阳轮齿根裂纹50%和断齿3种状态的实验数据进行评估,得到3种状态的裂纹评估结果分别为2.28%、51.95%、100%,与实际裂纹深度基本一致,验证了所提特征的有效性. 所提特征的计算过程需要用到啮合频率幅值和故障频率幅值,因此,啮合频率和故障频率提取的准确与否,将直接影响该特征的准确性. 由于该特征考虑到了不同齿轮具有不同的啮合频率、故障频率的因素,因此适用于不同齿轮的损伤程度评估,但不同齿轮的特征值变化趋势可能不同,需要具体分析.
