问题与征解

问题9(供题者：东南大学 陈建龙)设A为3阶实对称矩阵,它的3个特征值为λi(i=1,2,3)，满足λ1=λ2≠λ3，α1,α2为属于特征值λ1的线性无关的特征向量.请用λ1,λ3,α1,α2给出A的表达式.

问题10(供题者：湖南交通工程学院高科技研究院 冯良贵)设R={1,0,-1}，Rn×n为R上n阶方阵全体，证明：集合S={detA|A∈Rn×n} 必包含开区间(-2n-1,2n-1)内的一切整数.进一步，我们提出如下开放问题：S是否就由闭区间[-2n-1,2n-1]内的一切整数所构成呢?

问题2解答

以下解答由王尉(浙江大学数学科学学院的本科生，Email:3180104850@zju.edu.cn)提供.

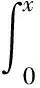
对于ε∈，[a,b]⊂，记

(1)

供题者点评提出此问题的背景是寻找刻画函数导数/梯度为零的条件，尤其是由函数的积分来表示的条件.王尉同学的解答挺好，能想到这样做很不容易.

问题3解答

问题3(供题者：厦门大学 林亚南)

(i)证明:对于数域F上任意的n阶矩阵A，存在可逆矩阵P使得B≡PA是对称矩阵.

(ii)设计一个算法，实现(i)的任务，即输入一个n阶矩阵A，输出相应的对称矩阵B.

以下解答由王中华(河南大学，Email：10100006@vip.henu.edu.cn)提供.

证(i)存在数域F上的可逆矩阵R和S，使得Ar=RAS，其中Ar为对角矩阵，r为矩阵A的秩.令P=(S-1)TR，B=PA，则B=PA=[(S-1)TR](R-1ArS-1)=(S-1)TArS-1,易见B是对称矩阵.

(ii)最后计算B=PA.算法实现的伪代码如下：

子程序a：输入一个矩阵，对其前n行作初等行变换，使前n行前n列其变为上三角矩阵；子程序b：输入一个矩阵，对其前n行作初等列变换，使前n行前n列其变为下三角矩阵；

1 输入矩阵A；

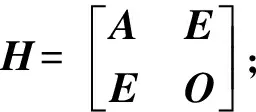
3 对H前n行、前n列分别作初等行、列变换，使其前n行前n列变为对角矩阵；

4 令R为H的前n行，后n列组成的矩阵，S为H的后n行，前n列组成的矩阵；

6 令P为K的后n列组成的矩阵；

7 输出B=PA.

供题者点评基于问题(i)证明的思想，解答者正确完整地回答了问题(ii).有没有可能直接给出算法呢？

问题4解答

问题4(供题者：复旦大学 谢启鸿 厉茗)设n阶复方阵A满足：对任意的正整数k，|Ak+In|=1.证明：A是幂零阵.

以下解答由伍诗颖(湖南第一师范学院2018级本科生，Email：sywu15211032635@163.com)提供，给出本题正确解答的还有周烁星(复旦大学2018级本科生).

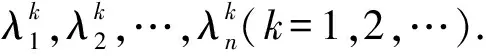
要证A幂零,即要证λ1=λ2=…=λn=0.将展开式

中的各项记作y1,y2,…,y2n-1.则对任何k=1,2,…,有

若y1,y2,…,y2n-1均为零，则结论得证.否则,设y1,y2,…,y2n-1中的所有不同的非零值为x1,x2,…,xm,且出现的次数依次为n1,n2,…,nm,则

解得n1=n2=…=nm=0.矛盾.因此，λ1=λ2=…=λn=0.即A幂零.