一个广受关注的数列极限的注记

杨 威， 李华冰

(1.合肥工业大学 数学学院，合肥 230601； 2.合肥工业大学 宣城校区基础部，安徽 宣城 242000)

1 引 言

类比是特殊到特殊的思维方式，是一种非常重要的数学思想，是提出新问题和作出新发现的重要源泉，可以培养学生的创新意识与创新能力.在高等数学中出现众多的类比.如低维与高维，离散与连续的类比等等.关于类比思想有众多的文献进行了阐述，读者可查阅相关文献.

受文献[1]的启发，文章用类比思维探讨了一个正切函数积分的数列极限问题，丰富了相关结论，对教学具有一定的参考价值.

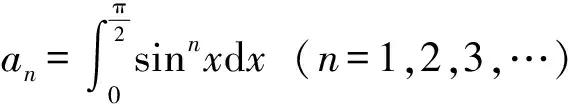
(1)

(2)

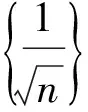
(3)

(4)

2 证 明

下面将基于类比思维，利用换元法和分部积分法，借助于数列的单调性，来给予证明.证明如下.

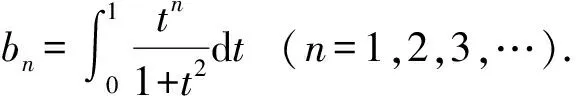
利用分部积分法可得

即

(5)

由此可知

从而(n+1)bn+1≥nbn，所以数列{nbn}单调递增.

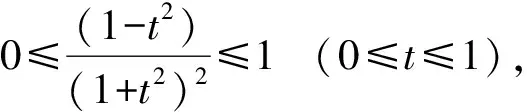
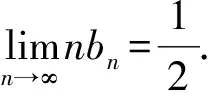
因此(4)式成立，从而(3)式也成立.

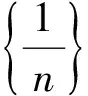
(4)式也可以用如下方法证明.

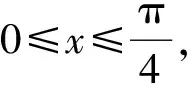
(6)

由于bn+2≤bn+1≤bn，所以由(6)知

(7)

(8)

由(7),(8)可得

(4)

3 应 用

下面举几个例子，说明(4)的应用.

在微积分中，有两个大家熟悉的结论，数列

(9)

(10)

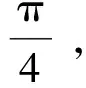
由于

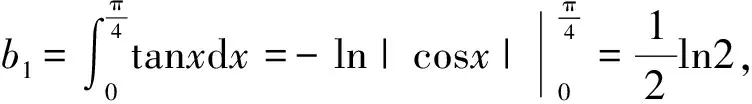
(11)

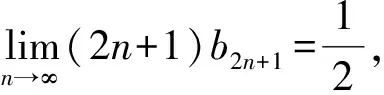
(12)

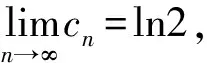
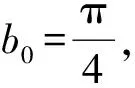
(13)

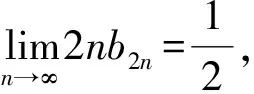
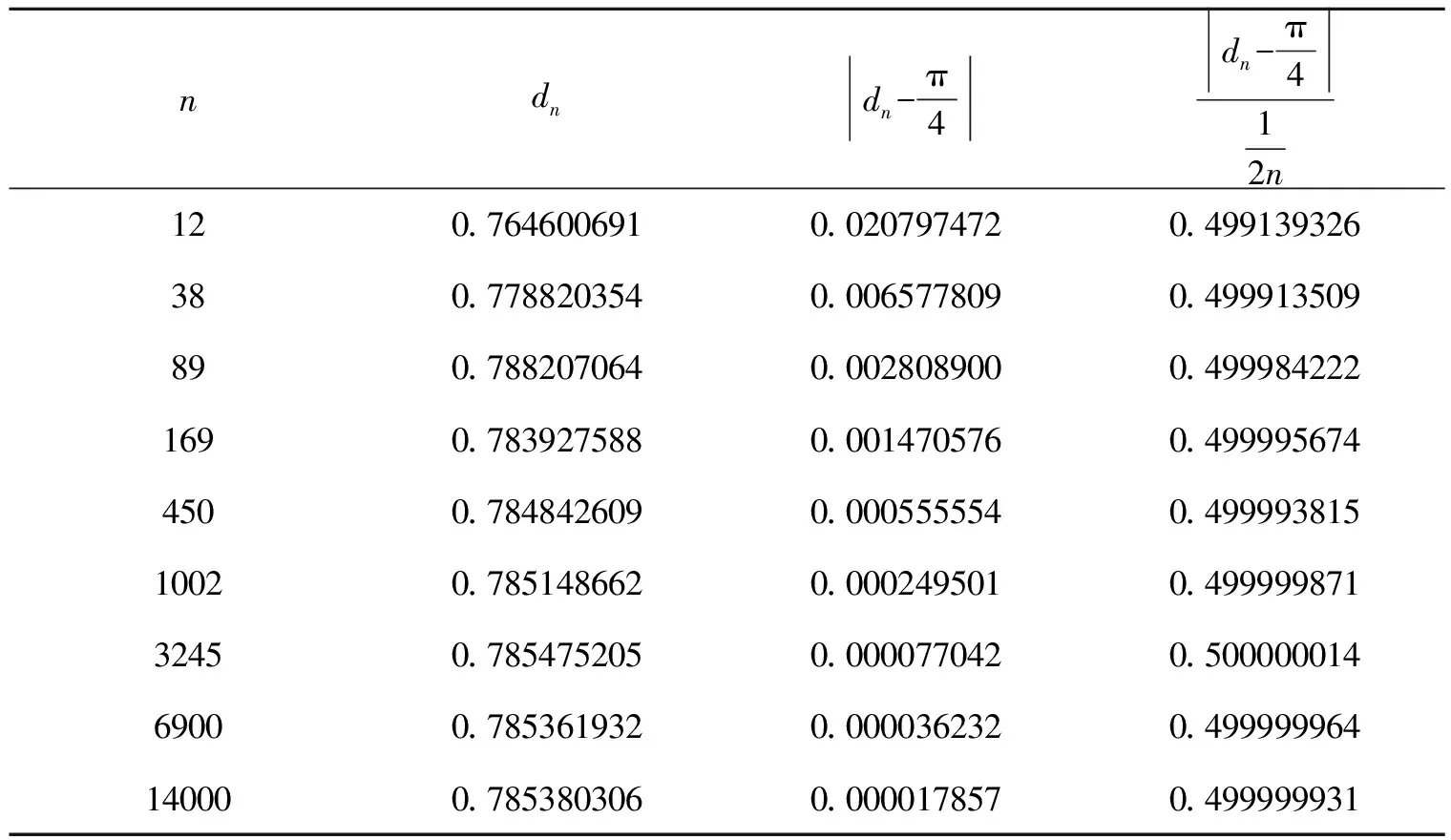
表1

4 结 论

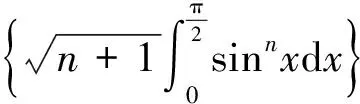
致谢审稿专家对文章的修改提了很多宝贵意见，在此表示感谢.