海底碎屑流冲击海底管道的模型与某一特定原型的相似性分析*

钱学生 徐景平

(①南方科技大学海洋科学与工程系， 深圳 518055， 中国) (②南方海洋科学与工程广东省实验室(广州)， 广州 511458， 中国)

0 引 言

海底碎屑流是最为典型的海洋地质灾害之一，通常是海底滑坡的主要产物，海底滑坡触发之后，高灵敏度海底沉积物的强度显著降低，且在沿海床面向下滑移的过程中与上层覆盖海水进行混合，形成海底碎屑流(吴时国等， 2009; Jia et al.，2016; 刘杰等， 2018; 王俊勤等， 2019)。海底碎屑流这一地质现象普遍存在于活跃三角洲附近和深水陆坡区，其速度高达30 m · s-1，密度可达1800 kg · m-3，受自身重力的驱动，可在平缓海床上进行长距离运移(Elverhøi et al.，2005)。海底管道是由海向陆输运海洋能源和矿产资源的重要生命线，虽然海洋工程地质勘察为其路由选址提供了充分的科学依据，但海底管道仍可能铺设在海底碎屑流的潜在影响区域(图 1)，因此，海底管道这一具有大跨度和低强度特点的关键工程设施将面临来自海底碎屑流的冲击威胁(李家钢等， 2012;Xiu et al.，2015; Dong et al.，2017; 厉成阳等， 2018)。以海底碎屑流为典型代表的失稳沉积物运动引起海底管道服役失效的工程案例屡见不鲜，例如，在1958～1965年期间，美国密西西比河口三角洲附近就有大约149次海底管道破坏事故是由海底沉积物运动引起的，而在1971～1975年期间该海域的失稳沉积物运动又导致了25起海底管道失效事件(Dutta et al.，2015)。近年来，随着铺设在深水陆坡的海底管道数量迅速增加，海底碎屑流对海底管道冲击的研究成为海洋工程地质灾害领域的前沿热点(Bruschi et al.，2006; Randolph et al.，2011; White et al.，2016; Malgesini et al.，2018)。

图 1 海底碎屑流对海底管道冲击影响示意图Fig. 1 Schematic of submarine debris-flow impact on undersea pipelines

海底碎屑流这一地质现象具有显著的偶发性，现有海底原位观测技术难以准确预测出它即将发生的时间和地点，同时，由于其具有极大的破坏性，即便能够预测出海底碎屑流的发生，也难以保证海底原位观测仪器不被冲毁而直接观测到它的运动速度和厚度等水动力参数。实际上，大多数海底碎屑流沉积体是在海底工程设施建设前通过海洋地球物理调查手段发现的，也有少数是在海底工程设施遭受破坏后识别出来的。在原位观测资料极其匮乏的条件下，学者们主要采用水槽实验(Zakeri et al.，2008; Haza et al.，2013)、土工离心机实验(Sahdi et al.，2014; 孙柏涛， 2014; 李家钢等， 2015)和数值模拟(Zakeri et al.，2009; 李宏伟等， 2015; Liu et al.，2015; 王忠涛等， 2016; Fan et al.，2018; Nian et al.，2018; Guo et al.，2019; Qian et al.，2020)的技术手段，对海底管道所受海底碎屑流的冲击力进行定量研究。考虑到水槽实验、土工离心机实验的易操作性和投资建造的经济可行性，以及数值模拟过程中的计算效率，学者们普遍采用缩小尺度的水槽实验、土工离心机实验和数值模型，模拟真实尺度条件下海底碎屑流对海底管道的冲击过程。其中：保证模型与某一特定原型之间的相似性是最为关键的技术环节之一，只有模型与该特定原型保持相似，才能将模型结果应用于原型工况。

在开展小尺度水槽实验和数值模拟研究的过程中，海底碎屑流冲击海底管道的模型通常处于常重力环境(1g)，此时黏性力占主导作用而重力影响很小，因此，应当采用雷诺相似准则保证模型与某一特定原型之间的相似性(左东启， 1984;Zakeri et al.，2008， 2009)。

基于雷诺相似准则，许多学者开展了常重力环境下(1g)海底碎屑流冲击海底管道的小尺度水槽实验和数值模拟研究工作(Zakeri et al.，2008， 2009;Zakeri， 2009; Haza et al.，2013; 李宏伟等， 2015; Liu et al.，2015; 王忠涛等， 2016; Fan et al.，2018; Nian et al.，2018; Guo et al.，2019;Sahdi et al.，2019; Qian et al.，2020)。表 1详细列出了部分研究工作中所采用的技术手段、本构关系、雷诺数范围、悬跨高度和冲击角度等关键信息。虽然学者们都已应用雷诺相似准则，但笔者认为已有研究未能保证模型与某一特定原型之间的相似性，这是因为雷诺相似准则要求某一特定模型工况(M1)与其对应原型工况(P1)的雷诺数相等，而已有研究仅满足多组次模型工况(M1，M2，…，Mn)与原型工况(P1，P2，…，Pn)的雷诺数范围相近，该特定模型工况(M1)与其对应原型工况(P1)的雷诺数并不相等，例如在Zakeri et al.(2008)的小尺度水槽实验中，仅满足多组次模型工况(2～140)与原型工况(0.6～240)的雷诺数范围相近，而在他们的数值模拟研究结果中，也仅满足多组次模型工况(1.7～320)与原型工况(0.6～240)的雷诺数范围相近(Zakeri et al.，2009;Zakeri， 2009)。

表 1 小尺度的水槽实验和数值模拟研究工作列举Table 1 Partial list of small-scale flume tests and numerical simulations

现有研究极少深入分析常重力环境下(1g)海底碎屑流冲击海底管道的小尺度水槽实验和数值模拟研究中模型与某一特定原型之间的相似性(Zakeri et al.，2008; Guo et al.，2018)，尚未发现模型与该特定原型之间的相似性存在问题，也未推导出模型与原型之间各物理参数的比尺关系。比尺关系在保证模型与某一特定原型相似的过程中发挥着至关重要的纽带作用，比尺关系的缺失将无法根据该特定原型工况设计出与其相似的模型工况，也无法根据某一特定模型工况推算出与其相似的原型工况。因此，亟待基于雷诺相似准则，针对常重力环境下(1g)海底碎屑流冲击海底管道的小尺度水槽实验和数值模型，推导出模型与原型之间各物理参数的比尺关系，据此分析模型与某一特定原型之间的相似性，为保证模型与该特定原型相似提供理论依据。

1 流变特性的描述

通常假设海底碎屑流为一种非牛顿流体，采用赫巴(Herschel-Bulkley)本构关系或幂律(Power-law)本构关系描述其流变特性(Zakeri et al.，2008)，其中剪切应力与剪切应变率之间的关系分别为：

(1a)

(1b)

2 雷诺数的定义

参照圆柱绕流问题中的雷诺数公式，可将海底碎屑流冲击海底管道的雷诺数定义为：

(2)

式中：Re为雷诺数；ρ为密度(kg · m-3)；U为速度(m · s-1)；D为管道直径(m)；μapp为表观黏度(Pa · s)。海底碎屑流是一种剪切稀化的非牛顿流体，其动力黏度随剪切应变率增大而减小，因此，式(2)中采用了海底碎屑流的表观黏度。表观黏度可定义为剪切应力与剪切应变率的比值：

(3)

式中： 剪切应变率可定义为速度和管道直径的比值：

(4)

将式(4)代入到式(3)中可得：

(5)

将式(5)代入到式(2)中，可得海底碎屑流冲击海底管道时的雷诺数(Zakeri et al.，2008)：

(6)

3 雷诺相似准则

为了使模型与某一特定原型之间保持相似，理论上要求组成模型与该特定原型的各物理量必须完全相似，但实际过程中难以做到。因此，针对某一具体问题，通常只考虑起主导作用的相似准则。例如，在开展水槽实验和数值模拟的过程中，缩小尺度的模型通常处于常重力环境(1g)，在研究海底碎屑流的运动和动力特性时，重力为主控因素而黏性力影响较小，须采用弗劳德相似准则保证模型与某一特定原型相似； 而在研究海底碎屑流冲击海底管道时，黏性力占主导作用而重力影响较小，故采用雷诺相似准则保证模型与某一特定原型相似(左东启， 1984;Zakeri et al.，2008， 2009)。雷诺相似准则要求模型工况与某一特定原型工况的雷诺数相等：

ReM=ReP

(7)

式中：ReM为模型雷诺数；ReP为原型雷诺数。因此，本文将基于雷诺相似准则，针对常重力环境下(1g)海底碎屑流冲击海底管道的小尺度水槽实验和数值模型，推导出模型与原型之间各物理参数的比尺关系。

4 比尺关系的推导

将模型与原型之间的长度比尺定义为：

(8)

式中：λ为长度比尺；DP为原型管道直径(m)；DM为模型管道直径(m)。由于模型中采用的海底碎屑流与原型一致，故模型与原型中海底碎屑流的密度和流变参数相同。由式(6)和式(7)可得：

(9)

式中：UM为模型速度(m · s-1)；UP为原型速度(m · s-1)；τM为模型剪切应力(Pa)；τP为原型剪切应力(Pa)。根据式(1a)中的赫巴本构关系，模型与原型的剪切应力可分别表达为：

(10a)

(10b)

将式(10a)和式(10b)代入到式(9)可得：

(11)

为了推导出模型与原型之间的速度比尺，需要化简式(11)。赫巴本构关系中引入了屈服应力项，导致难以进一步化简式(11)。为了解决该问题，笔者通过式(1b)中的幂律本构关系分别表达模型与原型的剪切应力：

(12a)

(12b)

将式(12a)和式(12b)代入到式(9)可得：

(13)

进一步化简式(13)，可得模型与原型之间的速度比尺：

(14)

根据长度比尺和速度比尺，可推导出模型与原型之间力的比尺：

(15)

式中：FP为原型冲击力(N)，FM为模型冲击力(N)。根据模型与原型之间的长度比尺和速度比尺，也可推导出其他常用物理参数的比尺关系，这里省略了推导过程而将推导结果直接列出(表 2)。根据模型与原型之间各物理参数的比尺关系，可设计出与某一特定原型工况相似的模型工况，也可基于已有的某一特定模型工况推算出与其相似的原型工况。

表 2 模型与原型之间各物理参数的比尺关系Table 2 Scale ratios between model and prototype for various parameters

5 比尺关系的应用举例

本文将根据推导得到的模型与原型之间各物理参数的比尺关系，对Zakeri et al.(2008)的水槽实验中模型与某一特定原型之间的相似性进行分析，试图推算出与现有水槽实验某一特定模型工况相似的原型工况，并设计出与他们预期的某一特定原型工况相似的模型工况。Zakeri et al.(2008)的水槽实验模型工况和预期的原型工况具体描述如下：

(1)模型工况：模型管道的直径为0.0286 m，海底碎屑流的冲击速度为0.5～1.4 m · s-1，共采用6种不同的海底碎屑流，其流变特性可通过赫巴本构关系和幂律本构关系分别描述(图 2)，其流变参数详见表 3。

图 2 基于赫巴本构关系和幂律本构关系的海底碎屑流流变曲线(改自Zakeri et al.，2008)Fig. 2 Flow curves of submarine debris flow characterized by Herschel-Bulkley and Power-law relations(modified from Zakeri et al.，2008)

表 3 基于Zakeri et al.(2008)水槽实验的海底碎屑流类型及流变特性Table 3 Type and rheology of submarine debris flow from Zakeri et al.(2008)flume tests

(2)原型工况：原型管道的直径为0.1～1 m，海底碎屑流的最大冲击速度为10 m · s-1，原型工况中采用的海底碎屑流种类与模型工况保持一致。

5.1 推算与某一特定模型工况相似的原型工况

根据模型与原型之间各物理参数的比尺关系(表 2)，可推算出与Zakeri et al.(2008)水槽实验某一特定模型工况相似的原型工况。当原型管道直径为0.1 m时，根据式(8)可得模型与原型之间的长度比尺：

(16)

以高岭土含量为10%的海底碎屑流为例(表 3)，根据式(14)可得模型与原型之间的速度比尺：

(17)

根据式(17)可计算得到与该特定模型工况相似的原型工况的最小和最大冲击速度：

UP，min=0.91×0.5 m·s-1=0.455 m·s-1

(18a)

UP，max=0.91×1.4 m·s-1=1.274 m·s-1

(18b)

式中：UP，min为原型最小冲击速度(m · s-1)；UP，max为原型最大冲击速度(m · s-1)；UM，min为模型最小冲击速度(m · s-1)；UM，max为模型最大冲击速度(m · s-1)。同理可得其他5种海底碎屑流条件下与该特定模型工况相似的原型工况的最小和最大冲击速度，这里省略了求解过程而将计算结果直接列出(表 4) 。类似的，当原型管道直径为1 m时，根据式(8)可得模型与原型之间的长度比尺：

(19)

表 4 基于Zakeri et al.(2008)水槽实验的模型与某一特定原型相似性分析结果Table 4 Results of model-prototype similarity analyses for Zakeri et al.(2008)flume tests

以高岭土含量为15%的海底碎屑流为例(表 3)，根据式(14)可得模型与原型之间的速度比尺：

(20)

根据式(20)可计算得到与该特定模型工况相似的原型工况的最小和最大冲击速度：

UP，min=0.789×0.5 m·s-1≈0.395 m·s-1

(21a)

UP，max=0.789×1.4 m·s-1≈1.105 m·s-1

(21b)

同理可得其他5种海底碎屑流条件下与该特定模型工况相似的原型工况的最小和最大冲击速度，这里省略了求解过程而将计算结果直接列出(表 4)。通过分析Zakeri et al.(2008)水槽实验中某一特定模型与原型之间的相似性可知，当模型管道的直径为0.0286 m，原型管道的直径为0.1 m时，与该水槽实验某一特定模型工况相似的原型工况中海底碎屑流最大冲击速度为1.302 m · s-1； 而当原型管道的直径为1 m时，原型工况中海底碎屑流最大冲击速度为1.138 m · s-1。显然，原型工况中海底碎屑流的最大冲击速度与Zakeri et al.(2008)预期的最大冲击速度10 m · s-1相差甚远。因此，Zakeri et al.(2008)的水槽实验模型工况与他们预期的某一特定原型工况并不相似。

5.2 设计与某一特定原型工况相似的模型工况

根据模型与原型之间各物理参数的比尺关系(表 2)，可设计出与Zakeri et al.(2008)预期的某一特定原型工况相似的模型工况。当原型管道的直径为0.1 m时，模型与原型之间的长度比尺可由式(16)计算得到。以高岭土含量为20%的海底碎屑流为例(表 3)，根据式(14)可得模型与原型之间的速度比尺：

(22)

根据式(22)可计算得到与该特定原型工况相似的模型工况的最大冲击速度：

(23)

同理可得其他5种海底碎屑流条件下与该特定原型工况相似的模型工况的最大冲击速度，这里省略了求解过程而将计算结果直接列出(表 4)。类似的，当原型管道的直径为1 m时，模型与原型之间的长度比尺可由式(19)计算得到。以高岭土含量为25%的海底碎屑流为例(表 3)，根据式(14)可得模型与原型之间的速度比尺：

(24)

根据式(24)可计算得到与该特定原型工况相似的模型工况的最大冲击速度：

(25)

同理可得其他5种海底碎屑流条件下与该特定原型工况相似的模型工况的最大冲击速度，这里省略了求解过程而将计算结果直接列出(表 4)。通过分析Zakeri et al.(2008)水槽实验中模型与某一特定原型的相似性可知，当原型管道的直径为0.1 m时，模型工况中海底碎屑流的最大冲击速度为10.988 m · s-1； 当原型管道的直径为1 m时，模型工况中海底碎屑流的最大冲击速度为13.067 m · s-1。此时的模型工况才与Zakeri et al.(2008)预期的某一特定原型工况相似。

6 比尺关系的适用性讨论

常规水槽实验通常用于研究水动力学、泥沙运动力学及与结构物相互作用问题，土工离心机实验通常用于研究土力学问题。表 2中列出的模型与原型之间各物理参数的比尺关系是基于幂律本构关系和雷诺相似准则推导而得，适用于常重力环境下(1g)海底碎屑流冲击海底管道的小尺度水槽实验和数值模拟研究。

然而，表 2中的比尺关系并不适用于土工离心机实验，这是因为土工离心机实验的比尺关系并非基于雷诺相似准则推导而得。土工离心机实验的相似准则要求模型与原型之间的应力状态相同，为此，将缩小尺度的模型置于超重力环境(Ng)，通过人工离心力场提高模型所受的体积力，以补偿模型因尺寸缩小而造成的应力损失(Schofield， 1980; 包承纲等， 1998)。根据土工离心机的相似原理，即缩小N倍的模型在承受N倍的重力加速度时其应力状态与原型相同，可以推导得到模型与原型之间各物理参数的比尺关系(表 5)(孙柏涛， 2014)。根据表 5 列出的土工离心机实验中模型与原型的比尺关系可以发现，利用土工离心机模拟海底碎屑流冲击海底管道的模型工况始终与其对应的原型工况保持雷诺数和弗劳德数相等，即自然满足雷诺相似准则和弗劳德相似准则。因此，在模拟海底碎屑流冲击海底管道时，土工离心机实验能够使模型与某一特定原型之间更多物理量(如应力、雷诺数和弗劳德数等)自然相似，从而比常规水槽实验更具一定的优势。

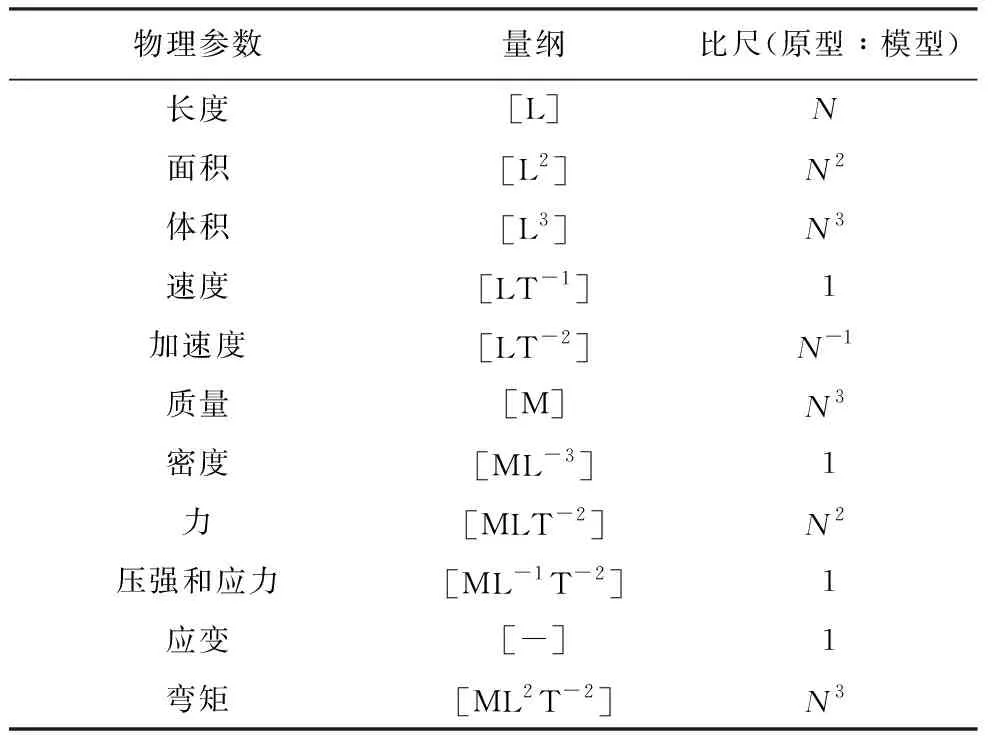
表 5 土工离心机实验中模型与原型之间各物理参数的比尺关系(孙柏涛， 2014)Table 5 Scale ratios between centrifuge model and prototype for various parameters(Sun， 2014)

为了展示表 2 和表 5 列出的比尺关系分别在水槽实验和土工离心机实验中的具体应用，本文针对水槽实验(Zakeri et al.，2008)和土工离心机实验(Sahdi et al.，2014)中雷诺数相近的海底碎屑流冲击海底管道的某一特定模型工况，分别推算出与它们相似的原型工况，并对比分析雷诺数相近时单位长度海底管道所受海底碎屑流冲击力的差异及成因。该水槽实验和土工离心机实验某一特定模型工况和推算得到的原型工况分别描述如下：

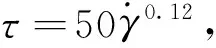
根据式(6)可得海底碎屑流冲击海底管道的雷诺数：

(26)

根据表 2 中的比尺关系，可得水槽实验工况中模型与原型之间的长度比尺、速度比尺和力的比尺：

(27a)

(27b)

(27c)

根据式(27a)、式(27b)、式(27c)可分别计算得到与该特定模型工况相似的原型工况的管道长度、冲击速度和冲击力：

LP=28×0.2 m=5.6 m

(28a)

UP=0.81×1.34 m · s-1≈1.08 m · s-1

(28b)

FP=511.4×14.3 N≈7313 N

(28c)

式中：LP为原型管道长度(m)；LM为模型管道长度(m)。根据式(28a)、式(28c)可计算得到原型工况中单位长度海底管道所受海底碎屑流的冲击力：

(29)

(2)土工离心机实验工况(Sahdi et al.，2014)：海底碎屑流的冲击速度为2.49 m·s-1，密度为1339 kg · m-3，参考不排水剪切强度为120 Pa，参考剪切应变率为0.2 s-1，变化指数为0.1，模型管道的直径为0.02 m，长度为0.12 m，模型管道所受的冲击力为14.4 N，土工离心机的离心加速度为40g。

首先，计算得到有效不排水剪切强度：

≈228.3 Pa

(30)

τ=Su-op=228.3 Pa

(31)

根据式(6)可得海底碎屑流冲击海底管道的雷诺数：

(32)

根据表 5 中的比尺关系，可得土工离心机实验工况中模型与原型之间的长度比尺、速度比尺和力的比尺：

λ=40

(33a)

(33b)

(33c)

根据式(33a)、式(33b)、式(33c)可分别计算得到与该特定模型工况相似的原型工况的管道直径、管道长度、冲击速度和冲击力：

DP=40×0.02 m=0.8 m

(34a)

LP=40×0.12 m=4.8 m

(34b)

UP=1×2.49 m · s-1=2.49 m · s-1

(34c)

FP=1600×14.4 N=23040 N

(34d)

根据式(34b)、式(34d)可计算得到原型工况中单位长度海底管道所受海底碎屑流的冲击力：

(35)

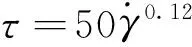
虽然两组原型工况中海底碎屑流冲击海底管道的雷诺数非常接近，但是单位长度海底管道所受冲击力的差异却十分明显。以下将借助流体力学中的拖曳力公式对这一差异的成因做简要说明，单位长度海底管道所受冲击力可表达为：

(36)

式中：FD为单位长度海底管道所受冲击力(N·m-1)；CD为拖曳力系数，通常视之为雷诺数的函数(Zakeri et al.，2008)。由于两组原型工况的雷诺数非常接近，故认为它们的拖曳力系数近似相等。根据式(36)可估算出两组原型工况中单位长度海底管道所受冲击力的比值：

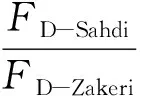
≈4.2

(37)

通过上述分析可知，两组原型工况中单位长度海底管道所受冲击力比值的估算值(4.2)与实际值(3.7)较为接近，由此说明采用流体力学中的拖曳力公式评估单位长度海底管道所受海底碎屑流的冲击力具有可行性。分析拖曳力公式中包含的各个物理量发现：雷诺数相近时，单位长度海底管道所受海底碎屑流冲击力的差异主要是由两组原型工况中不同海底碎屑流的密度和冲击速度引起的。其他因素也可能会导致雷诺数相近时单位长度海底管道所受冲击力的差异，但不在本文的讨论范畴。

7 结 论

本文基于幂律本构关系和雷诺相似准则，对海底碎屑流冲击海底管道时模型与原型之间各物理参数的比尺关系进行了推导，依据该比尺关系对Zakeri et al.(2008)的水槽实验中模型与某一特定原型之间的相似性进行了分析，基于Zakeri et al.(2008)的水槽实验和Sahdi et al.(2014)的土工离心机实验，对该比尺关系的适用性进行了讨论，得出如下结论：

(1)基于幂律本构关系和雷诺相似准则，推导出海底碎屑流冲击海底管道时模型与原型之间各物理参数的比尺关系，为保证模型与某一特定原型之间的相似性提供理论依据。该比尺关系适用于常重力环境下(1g)的小尺度水槽实验和数值模型，而不适用于超重力环境下(Ng)的土工离心机实验，也不适用于海底碎屑流的低剪切应变率工况，有关剪切应变率的影响未来仍需开展深入研究。

(2)通过分析Zakeri et al.(2008)水槽实验中模型与某一特定原型之间的相似性可知：该水槽实验模型工况与预期的某一特定原型工况并不相似，这是因为水槽实验中仅满足多组次模型工况(M1，M2，…，Mn)与原型工况(P1，P2，…，Pn)的雷诺数范围相近，而某一特定模型工况(M1)与其对应原型工况(P1)的雷诺数并不相等。

(3)通过分析Zakeri et al.(2008)水槽实验中模型与某一特定原型之间的相似性发现：当模型管道的直径为0.0286 m，原型管道的直径为0.1 m时，与该水槽实验某一特定模型工况相似的原型工况中海底碎屑流最大冲击速度应为1.302 m · s-1； 当原型管道的直径为1 m时，原型工况中海底碎屑流的最大冲击速度应为1.138 m · s-1。为了研究Zakeri et al.(2008)预期的海底碎屑流最大冲击速度为10 m · s-1、原型管道的直径为0.1 m的原型工况，模型工况中海底碎屑流的最大冲击速度应为10.988 m · s-1； 当原型管道的直径为1 m时，模型工况中海底碎屑流的最大冲击速度应为13.067 m · s-1。