考虑波浪与地震动力效应的曹妃甸海底斜坡稳定性探讨*

2022-01-22年廷凯付崔伟张建锁廖鑫昌

工程地质学报 2021年6期

张浩荣泽年廷凯付崔伟张建锁廖鑫昌

(大连理工大学，海岸和近海工程国家重点实验室，大连 116024，中国)

0 引言

海底斜坡失稳引发的滑坡作为一种破坏力较大的海洋地质灾害，威胁着人类工程活动和生命财产安全(李琳琳等， 2020)。前人采用各种方法开展了海底斜坡稳定性分析，如数值分析方法(Cao et al.，2013；金晓杰， 2013)、极限分析法(年廷凯等， 2016)、Newmark位移法(Lee et al.，1999； Urgeles et al.，2002；褚宏宪等， 2017)、极限平衡法等，其中极限平衡法是最常用也是最简单有效的一种方法。

波浪、地震等复杂荷载将引发海底岩土体破坏，导致大规模海底斜坡失稳(司少文等， 2021)。以往研究主要关注波浪和地震荷载的静力作用，众多学者以极限平衡法为手段，对波浪、地震荷载作用下的海底斜坡稳定性进行研究。在波浪荷载方面：孙永福等(2006)以极限平衡法对黄河水下三角洲斜坡稳定性进行评价，分析了极端海况土体滑移破坏的可能性，并对其失稳机理进行探讨；方中华等(2015)利用极限平衡法评价简化波浪作用下曹妃甸海底斜坡稳定性，为工程建设提供设计依据；褚宏宪等(2016)对自然状态和工程建设后的曹妃甸海底斜坡进行稳定性评价，确定了海底斜坡失稳空间特征，为工程建设提供了参考。在地震荷载方面：张伟等(2005)以圆弧条分法对厦门近岸的典型海底斜坡进行了地震稳定性评价；张亮等(2012)考虑南海北部陆坡软弱夹层影响，采用极限平衡法对拟静力地震荷载条件下的斜坡稳定性进行了评价； Lacasse et al. (2013)分别采用一维和二维极限平衡法对挪威 Lofoten-Vesteralen 陆坡的地震稳定性进行分析，确定了地震重现期对于斜坡稳定性的影响；修宗祥等(2016)考虑了土体非均质性，基于极限平衡方法对地震荷载下南海荔湾3-1气田管线路由海底峡谷段典型斜坡的稳定性进行了分析，结果表明地震水平加速度明显降低了该区域斜坡的稳定性。

综合而言，前人已经开展了大量研究，但目前仍存在不少问题：(1)极限平衡法分析波浪荷载，目前主要使用艾里波理论进行简化，得到其对海底面的压力，随着深度不同，压力会逐渐减小，但是现阶段计算所用简化后的艾里波荷载未完全反映波浪在海底土体上的拉压交替作用特点； (2)通用的拟静力方法将地震力视为恒定荷载，但真实的地震动力会随着时间变化而改变，引发孔隙水压力动态变化，显著影响斜坡稳定性结果； (3)动力荷载会引发土体强度弱化问题，即波浪和地震荷载将会改变海底斜坡坡面形态并弱化岩土体强度，降低复杂荷载作用时边坡的安全系数(Rodriguez-Ochoa et al.，2015；Zheng et al.，2019)，忽略侵蚀和弱化则会存在安全隐患，当遇到极端波浪和地震荷载，斜坡容易发生严重失稳破坏，造成更大损失。因此考虑真实荷载的动力效应、侵蚀和强度弱化对于海底斜坡稳定性研究具有重要的现实意义。

为此，本文基于曹妃甸海底斜坡案例，将有限元法和极限平衡法相结合，考虑简化波浪荷载和地震荷载的动力效应，开展海底斜坡的动态稳定性分析工作。深入研究极端波浪荷载和地震荷载下边坡的破坏模式，探讨侵蚀与岩土体强度弱化后的海底斜坡稳定性变化规律以及海底斜坡形态改变和强度弱化对斜坡稳定性的影响机制。

1 曹妃甸海底斜坡工程地质条件

曹妃甸又名“沙垒甸”，地处唐山市南部沿海，位于中国渤海北部海岸线上，如图 1 所示。强烈的水动力环境和泥沙运动导致曹妃甸港区海底地形非常复杂。由于潮流的作用，港区南部深槽发育良好，深槽的坡度也相对较陡，约为4°～9°(方中华， 2014)。

图 1 曹妃甸港位置图Fig. 1 Location of Caofeidian Port

取曹妃甸港区南部深槽处南北方向坡度最陡处截面为最典型截面，建立曹妃甸海底斜坡模型，如图 2 所示。其中斜坡剖面南北向距离约1500 m，定义平均海平面高程值为0 m，取海底面以下80 m范围内土层厚度，共分6个土层，主要物理力学参数见表 1。海平面下的土取饱和重度，斜坡北部①粉细砂层岩土体露出水面部分，在计算中取天然重度17.6 kN · m-1，总体采用有效应力准则，计算不同工况下的曹妃甸海底斜坡稳定性。

图 2 典型海底斜坡剖面图Fig. 2 Cross-section of typical submarine slope

表 1 曹妃甸海底斜坡物理力学性质指标(褚宏宪等， 2016)Table 1 Physical and mechanical properties of Caofeidian submarine slope

2 海底斜坡稳定性分析方法

在海底斜坡稳定性评价中，基于Geo-Studio程序，利用有限元法获得斜坡体内部的渗流场和动应力场分布，结合极限平衡法完成稳定性评价，具体过程如下。

首先建立力学计算模型，考虑计算精度与计算效率，以先整体划分、后局部加密方式进行有限元网格剖分，使用边界长度10 m的三角形与四边形单元对整体区域进行网格剖分，对可能出现临界滑动面的①、②土层区域单元设定边界长度1 m进行加密。共计得到26 773个节点， 26 254个单元，见图 3。

图 3 网格剖分图Fig. 3 Mesh grid

考虑渗流场地下水渗流和超孔隙水压力消散。在任一点处一定时间内流体流入流出单元体的差等于土体系统储水量的变化，即x和y方向外部施加的通量之和改变率等于单位体积含水量的改变率，二维渗流一般控制方程可表示为：

(1)

∂θ=mw∂uw

(2)

式中：H为总水头；kx为x方向渗透系数；ky为y方向渗透系数；Q为施加的边界流量；θ为单位体积含水量；t为时间；mw为储水曲线的斜率；uw为孔隙水压力。

对于瞬态问题，单位体积含水量的变化通过式(2)与孔隙水压力联系。应用加权余量的伽辽金方法求解控制方程，简化可得到瞬态二维渗流方程的有限元格式：

[K]{H}+[M]{H}，t={Q}

(3)

式中： [K]为单元特征矩阵； [M]为单元质量矩阵； {H}为节点水头向量； {H}，t为 {H}对时间t的导数； {Q}为单元上施加的流量矢量。

通过计算有限元控制方程，可以求解渗流场，得到各个单元的孔隙水压力uw。

然后考虑动应力场，分析由于地震冲击波动态载荷作用下的土动力学问题。系统动态响应的控制运动方程可以表示为式(4)，其中对于荷载向量，由体荷载、边界荷载作用力、集中荷载作用力和地震荷载作用力共同组成，即式(5)。地震力荷载通过节点加速度向量和质量矩阵作积得到，即式(6)，以Cholesky法求解有限元方程得到海底斜坡地震动力作用下的每一单元、每一高斯点应力及应变。

(4)

{F}={Fb}+{Fs}+{Fn}+{Fg}

(5)

(6)

进一步，结合极限平衡法，取拟分析圆弧滑动面，将滑动面上的岩土体划分为设定数目的条块，滑动面则由若干个条块底面组成。映射有限元高斯值到节点并取平均值，得到极限平衡法滑动面上各底面中心的应力状态f，见式(7)。依据莫尔圆方程计算得到底面中心的正应力和下滑剪应力，见式(8)。

f=[N]{FG}

(7)

(8)

式中： [N]为插值函数矩阵； {FG}为高斯点的应力值向量。

据已得到的海底斜坡正应力和下滑剪应力，对拟分析圆弧滑动面进行分析：对每一个条块，记底面长度为β，底部作用的下滑力为Sm，底部抗剪力为Sr(由抗剪强度有效应力指标c′、φ′计算得到)，对滑动面上条块底部应力直接积分，按下式计算安全系数Fs。

(9)

通过滑动面搜索与计算，找到最小安全系数圆弧面为临界滑动面。至此完成安全系数计算，用于海底斜坡稳定性评价。

3 考虑极端波浪的海底斜坡稳定性

当未遇极端波浪灾害时，曹妃甸港海底斜坡上主要存在两种工况：其一是海平面高程为0 m时的天然工况，其二是考虑曹妃甸地区大落潮(张娜等， 2020)时海平面绝对高程从5 m骤降至- 2 m的大落潮工况。天然工况下计算安全系数为5.973，斜坡稳定性良好；大落潮工况下，安全系数降为5.672，这是因为由于瞬态水降，引发了顺坡向的渗流，使得斜坡稳定性有所降低。在此基础上讨论极端波浪灾害的影响。

极端波浪荷载会增加岩土体剪切应力，激发土体产生超孔隙水压力，引起斜坡土体失稳(孙永福等， 2006)。海洋中的波浪形式多样，对于开阔地势及较为规则的海底斜坡上波浪荷载的模拟，通常以艾里波理论表示。对于斜坡受力，波浪的波高、波长和水深是影响稳定性的重要因素。艾里波理论中一阶线性波波浪t时刻对于横坐标为x海底斜坡表面某点的波压力p可表示为(刘敏等， 2015；刘博等， 2016)：

p=p0sin(λx-ωt)

(10)

(11)

式中：p为距离水面平均深度为H的海底地面受到的理论波压力(kPa)；p0为波浪引起的海底压力变化幅值(kPa)；γw为海水的重度，取10.3 kN · m-3；H为海底面距离水面的深度(m)；Lw为波长(m)；h为波高(m)；T为周期(s)；ω为波浪的圆频率，表示为ω=2π/T；λ为波数，可表示为λ=2π/Lw， 1/m。

图 4 不同时刻波浪荷载简化示意图Fig. 4 Simplified diagram of wave load at different timea. t=0； b. t=T/2

波浪的重现期为不同程度的波浪出现一次的平均间隔时间，本文分别考虑重现期为5 a和50 a的波浪对于曹妃甸港海底斜坡的影响。重现期5 a波长取80 m，波高取3.75 m，周期取7.69 s；重现期50 a波长取90 m，波高取4.78 m，周期取8.60 s。

利用上述方法，可计算曹妃甸海底斜坡不同重现期波浪荷载工况下的安全系数，结果如表 2 所示。

表 2 不同重现期波浪荷载作用下安全系数Table 2 Safety factors of submarine slopes under wave loads with different recurrence intervals

对于重现期为5 a的波浪，波长与波高相对较小，波浪荷载作用下的斜坡尚处于稳定。但相较于水面为0的无波浪情况，安全系数下降了3左右，可见波浪荷载对海底斜坡稳定性影响显著。对于重现期为50 a的波浪，斜坡安全系数稍大于1，已临近失稳。可知在巨浪循环拉压荷载作用下，海底斜坡极易失稳。相较于单一波浪荷载方向简化方式，分段拉压荷载施加方式获得更低的安全系数，更能体现波浪荷载真实作用，可为极端波浪荷载作用下的海底斜坡相关设计和评价提供参考。

4 考虑地震动力效应海底斜坡稳定性

地震作用会使海底斜坡孔隙水压力累积上升、土体强度降低，引起土体塑性变形、砂土液化等问题，最终导致斜坡失稳破坏(褚宏宪等， 2016)。本文分别考虑拟静力和动力地震荷载作用，开展海底斜坡稳定性分析与评价，具体过程如下。

4.1 拟静力加载法

以拟静力法加载，普遍用地震系数KE来描述：

(12)

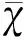
依据《建筑抗震设计规范》(GB50011-2010)，列出地震烈度与地震系数的关系(表 3)，曹妃甸处于7度0.15g烈度区，按8度近震设计地震加速度值作为曹妃甸地区可能遇到的最不利的地震荷载进行模拟。

表 3 曹妃甸海底斜坡地震设防烈度与计算安全系数关系表Table 3 Relationship between the seismic fortification intensity of the Caofeidian submarine slope and the calculated safety factor

因此设置工况中地震系数为0.05～0.20g。利用拟静力加载法，计算可得各地震加速度值下曹妃甸天然海底斜坡安全系数，结果见表 3。可知，当地震加速度值小于加速度设定值0.15g时，斜坡尚安全；处于加速度设定值情况下，安全系数稍大于1，临界于破坏状态；当地震加速度值大于烈度区地震加速度设定值情况下，斜坡安全系数小于1，已破坏。

4.2 动力加载法

依据历史上唐山地区地震波数据(峰值加速度为0.477g)，以曹妃甸地区地震烈度设计加速度0.15g为峰值进行整体等效修正，修正后加速度时程曲线如图 5a 所示。设定海底斜坡边界条件为左右边界辊支撑(水平方向固定、竖向自由运动)，底面为固定支撑，而后开展有限元和极限平衡法计算，得到安全系数为0.678。相比于拟静力荷载，安全系数大幅度下降，斜坡已严重失稳。

为了描述岩土体变形，以Newmark法计算岩土体位移，基本原理是获得有限元计算斜坡土体应力后，减去初始静应力σs即获得动应力，在整个滑面累加得到总动剪力，即由地震引起的附加剪力。将总动剪应力除以拟分析滑动面上岩土体重量W作为平均加速度值，与临界加速度ay作差后对时间t作二次积分，即得到地震累积的相对位移LE，表达式如下：

(13)

取临界滑裂面内拟滑动岩土体中心点(360，-30)为代表，研究其附近岩土体的相对位移值，如图 5b 所示。

图 5 地震动力效应图Fig. 5 Seismic dynamic effect diagrama. 地震时程曲线； b. 相对位移曲线

可以看出，相对位移整体先增大后减小，当t=12.0 s时位移达到最大值0.37 m。动态地震波使斜坡位移随时间波动，位移极值与地震时程曲线波峰相对应，地震波中期为最不利的阶段，此时中前期的地震波峰作用显现，同时新时刻的地震波峰也持续影响，使斜坡产生较大的位移，威胁其安全性。

5 特殊环境下海底斜坡稳定性

当海底斜坡遭受长期反复的极端波浪荷载作用时，冲刷侵蚀加剧，将导致海底斜坡形态发生改变(王艳等， 1999)。基于该斜坡的原始形态和土层状况，假定位于坡脚的粉细砂全部被侵蚀，形成新的斜坡，如图 6 所示。另外，极端波浪和地震动力作用下，斜坡土体会呈现强度弱化现象，且岩土体弱化程度为10%～20%，严重时高达50%或更多(Rodriguez-Ochoa et al.，2015)。鉴于曹妃甸海底斜坡尚未受到破坏性循环荷载，强度折减过大，斜坡自然状态失稳导致动力效应研究无现实意义等情况，本文分别考虑侵蚀但不发生弱化、侵蚀且发生10%弱化、侵蚀且发生20%弱化共3种情况，开展前述各类荷载条件下的海底斜坡稳定性计算分析，结果见表 4。

图 6 考虑侵蚀海底斜坡截面图Fig. 6 Cross-section of the eroded submarine slope

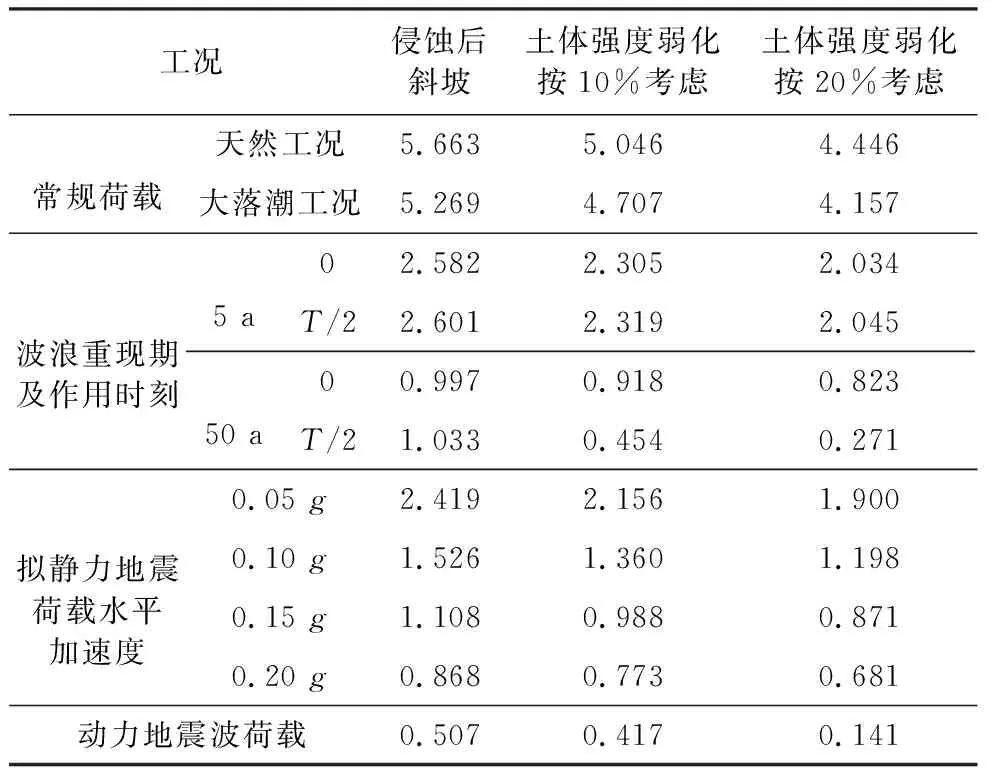
表 4 考虑坡面侵蚀与土体强度弱化后的海底斜坡稳定性Table 4 Stability evaluation of submarine slope after erosion and weakening

5.1 天然、大落潮工况下海底斜坡侵蚀弱化效应

海底斜坡未受侵蚀时天然工况和大落潮工况下计算安全系数分别为5.973和5.672。分析侵蚀导致斜坡形态改变的影响，即海底斜坡形态改变后，天然工况安全系数降低约0.3，大落潮工况降低约0.4，可以看出，单纯侵蚀方式导致海底斜坡形态改变并未使斜坡失稳，安全系数降低程度不明显。

将侵蚀后海底斜坡模型强度参数进行10%折减，考虑侵蚀与土体强度弱化共同作用，可以看出天然工况安全系数下降值约0.9，大落潮工况安全系数下降值接近1.0，两个效应的综合作用相较于单纯的侵蚀作用更易导致斜坡失稳。

考虑强度进一步弱化，对岩土体强度参数进行20%折减，两个工况的安全系数都下降了1.5左右，降低幅值相对较大，对斜坡的影响也较明显，因此考虑斜坡侵蚀及岩土体强度弱化效应是十分有必要。

5.2 极端波浪荷载下海底斜坡的侵蚀弱化效应

考虑到波浪荷载的周期性，t=T/2×i(i=0、2、4……)时，波浪作用下安全系数相等；同理t=T/2×i(i=1、3、5……)时，安全系数也相等。当波浪荷载重现期分别为5 a和50 a时，各取3个周期进行分析，计算结果如图 7 所示。

图 7 不同重现期波浪荷载作用下侵蚀弱化斜坡安全系数Fig. 7 Safety factor diagram of eroded and weakened slope under wave loads with different recurrence intervals

仅考虑斜坡的侵蚀效应时，对比未侵蚀斜坡和侵蚀后斜坡在波浪一个周期内最小安全系数变化情况。重现期为5 a和50 a的波浪荷载作用下，侵蚀工况下斜坡安全系数分别降低了约6.2%和2.3%。由此可见，侵蚀对重现期小的波浪荷载影响更明显；对于重现期更大的波浪，波浪破坏力为主要降低安全系数的因素，侵蚀变化导致的安全系数降低程度不明显。

考虑斜坡的侵蚀与弱化作用时，分析未侵蚀斜坡与侵蚀且强度弱化两种工况下斜坡在波浪一个周期内最小安全系数变化情况。重现期为5 a波浪荷载作用下，与未侵蚀斜坡相比，岩土体强度弱化10%和20%工况的安全系数分别降低了16.3%、26.1%。当重现期为50 a时，斜坡均已失稳，随着斜坡岩土体弱化程度增加，分别降低55.5%、73.4%，这是由于斜坡已处于严重破坏状态，强度弱化会使得安全系数产生较大程度的降低。

5.3 地震荷载下海底斜坡的侵蚀弱化效应

使用拟静力加载法计算地震作用下斜坡安全系数，取各工况下的安全系数值与水平地震加速度值进行分析，如图 8。由图可见，当水平地震加速度值逐级增大时，安全系数也逐渐下降，但下降幅度逐渐减小。当地震加速度小于等于0.10g，各工况斜坡均保持稳定；当加速度为0.15g，岩土体强度弱化10%和20%工况斜坡发生失稳；当加速度为0.20g，所有工况下的海底斜坡均失稳破坏。对应曹妃甸地区抗震设防烈度情况，未发生侵蚀与强度弱化前斜坡尚能保持稳定，一旦海底斜坡发生侵蚀和强度弱化，斜坡立即失稳破坏，由此可见，侵蚀和强度弱化已经成为了地震灾害中斜坡失稳破坏的重要因素。

图 8 不同地震烈度荷载作用下侵蚀弱化斜坡安全系数Fig. 8 Safety factor of eroded and weakened slope under different seismic intensity loads

由表 4 可知，当动态地震波作用于侵蚀后的斜坡时，地震荷载及动态水力变化导致斜坡受力增大，伴随着岩土体抗剪强度降低，安全系数大幅度下降，且弱化程度越大，破坏程度越强。本文研究中，当侵蚀与弱化20%时，海底斜坡处于最危险状态，安全系数为Fs=0.141，临界滑动面如图 9 所示。相较于静力法地震荷载，动态地震波对于斜坡的破坏更为严重。可见不能忽视复杂荷载造成斜坡侵蚀与岩土体强度弱化效应以及真实地震波所具有的动力效应。