黏土中水平受荷大直径单桩设计方法的对比研究*

周 媛 郑敬宾 王 栋

(①中国海洋大学山东省海洋环境地质工程重点实验室， 青岛 266100， 中国) (②中国海洋大学环境科学与工程学院， 青岛 266100， 中国)

0 引 言

随着不可再生资源的不断消耗，风力发电是目前世界上发展最快、最有商业价值的绿色能源技术之一，仅次于水力发电(李红有等， 2019)。近年来，随着海上施工和设计技术的提高，海洋已经成为一个迅速发展的风电市场。海上风机的基础形式多种多样，包括单桩、吸力基础(Ding et al.，2015； 陈林平等， 2020)、群桩支撑的高层承台基础(Qi et al.，2014)等，风机基础的研究对风机的顺利建设和安全使用意义重大(刘晓磊等， 2020)。在各种海上风机基础型式中：大直径单桩有施工便利、造价经济等优点，是当前应用最广泛的海上风机基础型式(Ramírez et al.，2020)。海上环境复杂多样，在海上风机运行过程中，主要受到风、浪、流等水平荷载的作用，如图 1所示。

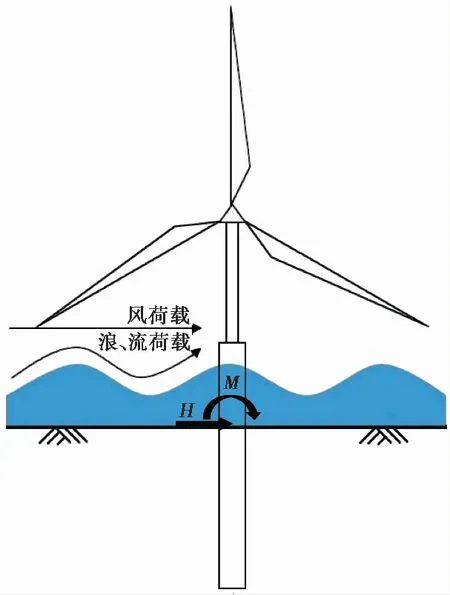
图 1 风机单桩基础受力图Fig. 1 Force diagram of monopile foundation

对于支撑海上风机的大直径单桩来说，其竖向承载力通常容易满足。但为了保障上部风机的正常使用极限状态，设计中对水平荷载作用下的桩头位移和转角有着极为严格的要求。例如DNV GL(2017， 2018)规范要求，海上风机单桩基础在设计使用年限内的桩顶累积转角不得超过0.5°(安装施工允许的0.25°误差也包含在内)。因此，大直径单桩的水平受荷响应一般是其设计的主控条件。

在设计时，人们普遍将上部结构所受水平荷载等效为泥线处的水平集中力(H)和倾覆力矩(M)。目前，应用最广泛的水平受荷桩分析方法是p-y曲线法，即将土体抗力简化为沿桩身分布的一系列非线性弹簧，采用弹簧响应来描述土体水平阻力p与桩身侧向位移y的关系，例如Matlock(1970)和Reese(1974)等基于现场试验提出的黏土与砂土中的p-y曲线。国内设计单位普遍依托API规范(API， 2014)，规范中推荐采用的是Matlock(1970)提出的p-y曲线。

API规范主要针对的是海上导管架平台的桩基础设计，建议的p-y曲线来源于直径D不超过2 m的桩基现场试验，理论上仅适用于大长径比的细长桩。然而，为了满足设计要求，目前海上风机一般采用大直径的单桩基础，常见直径范围达到D=4～7.5 m，长径比通常为L/D=2～6(Page et al.，2017)，远小于Matlock(1970)现场试验采用的L/D>10的桩基，对大直径单桩的桩身受力特性进行现场测试存在许多难点(马加骁等， 2020)。因此，API规范(2014)推荐的p-y曲线公式是否适合长径比较小的海上风机大直径单桩受到了广泛关注。已有研究表明(Byrne et al.，2015a, 2015b； 龚维明等， 2015； 孟晓伟等， 2019)，API规范推荐的方法可能过于保守，会低估黏土的初始刚度和极限抗力，导致设计的桩径和桩长过大，虽然能够达到安全标准，但在工程应用中不具有经济效益，而且会造成运输和安装困难。基于此，DNV GL(2018)规范建议在单桩设计中通过有限元分析校准弹簧响应。Byrne et al. (2015a, 2015b)通过现场试验发现，水平荷载作用于大直径单桩时，桩基除水平抗力外还会受到桩底集中力和桩身分布力矩等抗力作用。在土体多弹簧模型的基础上，有一些具有代表性的方法，其中Zhang et al. (2017a, 2017b， 2019)对黏土中大直径单桩(L/D=5～10)的土体反力弹簧进行了广泛的数值研究并指出，在大多数实际情况下，桩底的集中力矩反力可以忽略不计。张海洋等(2020)通过有限元模拟，将桩土界面粗糙度与桩径效应纳入考虑，对API方法中土体的极限承载力进行了修正，提出了适合大直径刚性桩的修正p-y曲线。Wang et al. (2020)通过离心机试验和数值模拟研究，认为水平受荷大直径单桩的旋转中心总在距离泥面约0.8L处，旋转中心以下的桩土响应可以等效为作用在该点的集中力矩。Fu et al. (2020)的有限元分析表明，大直径单桩桩身与桩底受到的摩擦力不可忽略，因此在分析计算时除了p-y曲线，还需要考虑反应桩身分布力矩和桩底剪力的弹簧模型。

本文通过比较现有规范和新近发展的3种静力荷载下水平受荷桩分析方法，并与模拟整桩水平响应的三维有限元结果进行对比，重点讨论已有方法的适用性和优缺点。以此为基础，研究不同长径比情况下，最适用于大直径单桩分析的设计方法中各个主要参数对预测结果的影响，总结影响水平受荷大直径单桩桩身响应的主要因素，为工程设计中大直径单桩分析方法的选取提供依据。

1 分析方法

本文对比的水平受荷桩分析方法包括：(a)API规范(2014)建议的桩身水平弹簧p-y曲线； (b) Zhang et al.(2017b)提出的桩身水平弹簧p-y曲线； (c) Wang et al. (2020)提出的考虑桩身弹簧p-y曲线和旋转中心弹簧MR-θR曲线的方法； (d) Fu et al. (2020)提出的同时考虑桩身水平弹簧p-y曲线、桩底剪力弹簧s-y曲线和桩身旋转弹簧m-θ曲线的方法，如图 2所示。

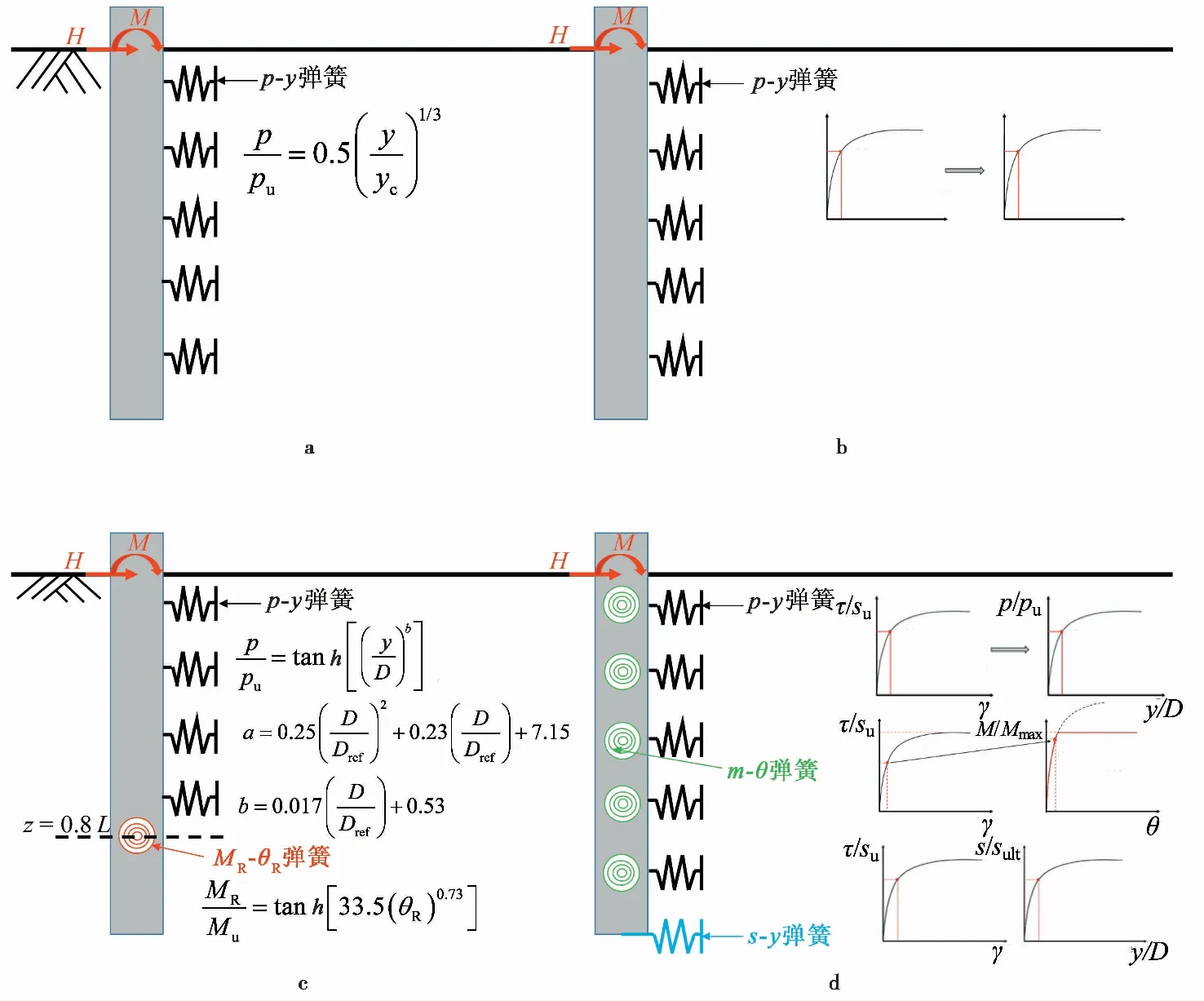
图 2 水平受荷桩分析方法示意图Fig. 2 Analysis methods for pile under horizontal loada. API规范法； b. Zhang et al.(2017b)方法； c. Wang et al.(2020)方法； d. Fu et al.(2020)方法

如前所述，API规范推荐的是Matlock(1970)提出的p-y曲线：

(1)

式中：p为水平抗力；pu为极限水平承载力并采用Matlock(1970)推荐的承载力系数；y为水平位移；yc=2.5×εc×D，其中，εc为原状土进行三轴不排水试验时50%最大偏应力对应的轴向应变，经验值一般取0.01。

Zhang et al. (2017b)建议按照一定比例缩放单剪试验的土体应力-应变(τ-γ)曲线(如图 2b所示)，以此得出适用于特定土体的p-y曲线。归一化水平抗力p/pu与归一化剪应力τ/su(su为单剪试验得到的不排水抗剪强度)对应，归一化水平位移y/D根据剪应变γ进行缩放，缩放关系如下：

(2)

(3)

式中： 计算pu时采用Zhang et al. (2017a)推荐的承载力系数； 系数ξe1=2.6和ξp1=1.35+0.25α基于平面应变条件下薄片“桩身-土”相互作用的有限元结果拟合得到；α为桩土界面粗糙系数(0≤α≤1)，α=0和1分别对应界面完全光滑和完全粗糙； 剪应变(γ)为弹性剪应变(γe)和塑性剪应变(γp)之和：

(4)

式中：γe=τ/Gmax，Gmax为土体初始剪切模量。

Wang et al. (2020)基于离心机试验和数值模拟结果，假定大直径单桩在受到水平荷载时，旋转中心总在泥面以下0.8L深度处，即y=0，旋转中心以下的桩土响应可以等效为作用在该点的集中力矩(如图 2c所示)。因此Wang et al. (2020)方法仅预测旋转中心以上部分的桩身响应。此时，桩身水平弹簧p-y曲线和旋转中心处集中力矩弹簧MR-θR曲线的表达式为：

(5)

a=0.25D2+0.23D+7.15

(6)

b=0.017D+0.53

(7)

(8)

(9)

式中： 计算pu时采用Jeanjean(2009)推荐的承载力系数；Mu为旋转中心的最大抗倾覆力矩；su-0.8L为表示距泥面0.8L深度处的土体不排水抗剪强度。

Fu et al. (2020)指出，与细长桩相比，大直径单桩水平受荷过程中产生的桩底剪切抗力以及桩身轴向摩擦导致的分布力矩不可忽略。因此，在Zhang et al. (2017b)方法的基础上提出了多弹簧梁柱模型，包括沿桩身分布的p-y水平弹簧和m-θ旋转弹簧以及桩底s-y剪力弹簧。每种弹簧响应都能与单剪试验的应力-应变(τ-γ)关系建立联系，其中水平弹簧响应仍然根据式(2)～式(4)确定。

归一化桩身分布力矩m/mmax和桩身转角θ与应力-应变曲线的缩放关系如下：

(10)

(11)

mmax=D2αsu

(12)

式中：m为桩身分布力矩；mmax为分布力矩的极限值； 系数ξe2=1.15，ξp2=0.17～0.5基于有限元结果和理论推导得到，Zhang et al.(2017b)建议取值ξp2=0.45。

与p-y曲线的缩放类似，归一化桩底剪力S/Sult随位移y/D的变化曲线与τ-γ曲线的缩放关系如下：

(13)

(14)

(15)

式中：S为桩底剪力；Sult表示桩底剪力极限值，等于土体不排水抗剪强度与桩底面积之积(式15)； 根据数值模拟结果拟合的系数ξe3=0.3，ξp3=0.12。

2 有限元模型与土体性质

为了验证上述水平受荷桩分析方法，本文开展了全面的桩土相互作用三维有限元分析。通过有限元模拟结果与不同分析方法预测结果的比较，探讨黏土中水平受荷大直径单桩分析方法的适用性。下面将对建立的有限元模型和采用的土体性质进行描述。

2.1 有限元模型

利用大型通用有限元软件ABAQUS建立图 3所示的有限元分析模型。考虑问题的对称性，采用半模型以提高计算效率。数值分析结果表明图 2所示的土体模型尺寸足以避免边界效应的影响。为了方便建模，基于抗弯刚度等效将钢管桩替换为实心桩。在本文的分析中，考虑钢管桩直径为D=6 m，壁厚t=0.06 m，等效抗弯刚度为1.04×109kN·m2。泥面以下的桩长L分别为30 m和60 m，相应的长径比L/D=5和10。桩头高出泥面30 m，通过在桩头施加不同大小的水平集中力，模拟桩基在泥面处受到的水平集中力和倾覆力矩。

图 3 黏土中水平受荷大直径单桩三维有限元模型(L/D=5)Fig. 3 Three-dimensional finite element model of monopile under horizontal load in clay(L/D=5)

采用一阶缩减积分六面体单元(C3D8R)离散土体和桩。为提高数值计算精度，在桩端附近区域以及以桩基轴线为中心，半径为2D的圆柱区域内划分更加精细的网格，最小单元尺寸为D/30。考虑桩基与黏土相互作用时接触面上产生吸力，因此假定桩-土接触面完全粗糙且不分离。该假定在黏土的“土-结构”相互作用有限元模拟中被广泛应用(Monajemi et al.，2009； Zou et al.，2018)。土体模型侧面与底部约束法向位移，对称面约束法向位移及绕对称面水平向和竖向的转角。需要注意的是，当采用基于总应力的土体模型模拟不排水条件时，土体的自重对其力学响应没有影响(Fu et al.，2020)，因此，下述有限元分析结果均假定土体是无重土。

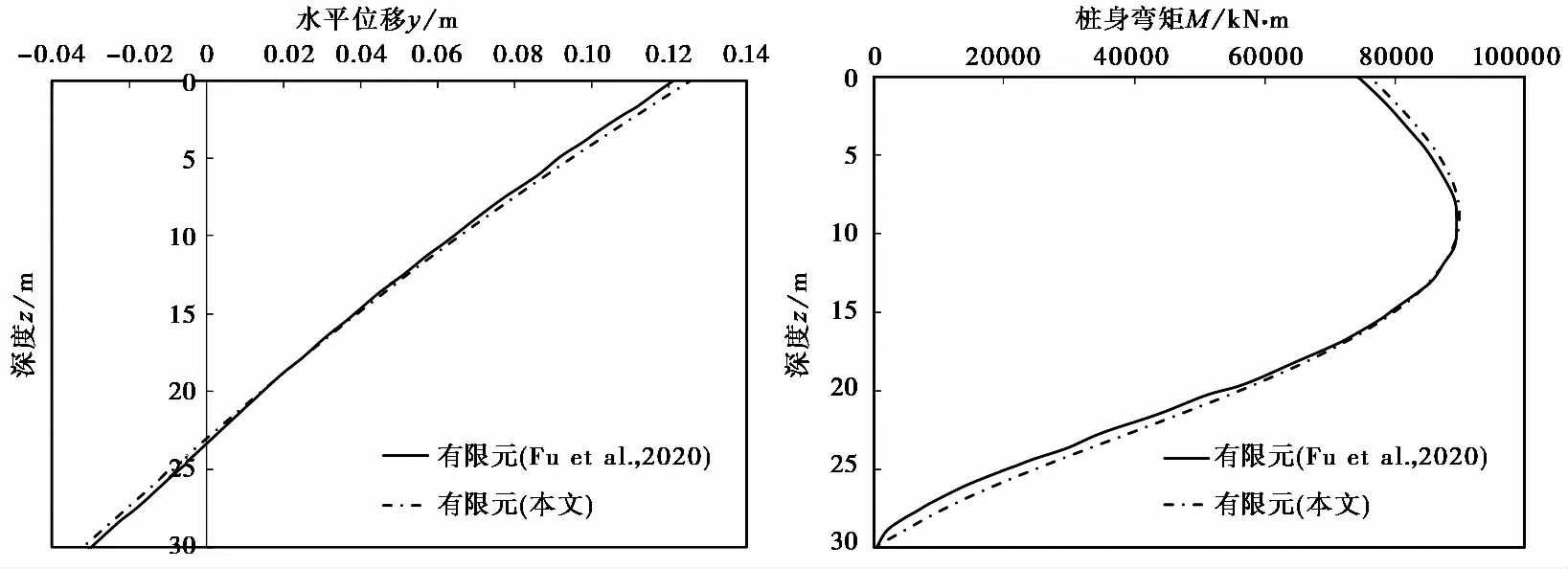
图 4 有限元结果对比图Fig. 4 Comparison of finite element analysis results

建立了与桩基长度相等、与桩基轴线重合的梁单元“beam”，并通过ABAQUS的“embedded region”约束设置，使其在分析过程中与桩基轴线具备相同的位移和变形。梁单元抗弯刚度设置为桩基的一百万分之一。通过上述设置，能够在结果中直接输出梁单元的弯矩，根据抗弯刚度缩小的比例，桩基的桩身弯矩是梁单元的一百万倍。

2.2 土体性质

采用Tresca模型描述土体的屈服响应。泊松比取0.49，充分考虑黏土完全不排水条件的同时保证了计算的收敛性。弹性模量E与不排水抗剪强度su之比保持定值，对应的剪切模量G可以通过下式计算：

(16)

为了能够灵活地考虑各种土体性质的不同，本文使用NGI-ADP模型(Grimstad et al.，2012)描述黏土不排水条件下的应力-应变曲线，其屈服应力τ与剪应变γ的关系如式(4)所示，包含弹性响应和塑性响应两部分。弹性响应中Gmax的大小通过式(16)计算，而塑性响应中屈服应力与塑性剪应变的关系采用下式计算：

(17)

2.3 有限元结果验证

3 方法对比

图 5 不同方法结果对比Fig. 5 Comparison of results on different methodsa. L/D=5，H=2000 kN，M=60 000 kN · m; b. L/D=10，桩顶H=5000 kN，M=150 000 kN · m

从图中可以看出，根据API方法求得的桩身水平位移和转角最大，而Wang et al.(2020)方法的预测的位移与转角最小。与有限元结果相比，当L/D=5时，Wang et al.(2020)方法低估了最大位移和转角(泥线处)约36.0%与31.8%，当L/D=10时，则分别低估了约26.3%与15.1%。由此可见，Wang et al.(2020)方法用于设计时可能会偏于危险。此外，从式(5)～式(9)可以看出，Wang et al. (2020)提出的p-y曲线与MR-θR曲线仅依赖于桩基直径的大小，无法考虑土体变形特性的影响。若土体刚度Gmax/su减小，Wang et al.(2020)方法将进一步低估桩身变形响应，造成对位移和转角的过分低估。不仅如此，Wang et al. (2020)方法中的公式仅适用于均质或强度随深度线性增加的黏土，对于强弱交替的多层土地层，无法代入梁柱分析模型进行分析计算。

Fu et al. (2020)方法与Zhang et al. (2017b)方法预测的位移和转角均小于API规范方法结果，但大于有限元结果。对于更接近于细长桩的情况(L/D=10)，这3种方法预测的位移和转角结果差别并不大。与有限元模拟得到的桩基泥面处位移相比，API方法、Zhang et al.(2017b)方法、Fu et al.(2020)方法分别高估了27.5%、16.6%和15.0%。对于长径比L/D=5的大直径单桩，API规范提供的设计方法过分保守，与有限元结果相比，分别高估泥面处位移和转角约5倍和4倍。在偏于安全的预测结果中，Fu et al. (2020)提出的基于3种土体弹簧模型的预测结果与有限元结果最为接近。这说明随着长径比的减小，桩身分布力矩与桩底剪力的影响随之增大。

综上所述，Fu et al. (2020)提出的同时考虑p-y曲线、s-y曲线和m-θ曲线的三弹簧模型更贴近大直径单桩的真实响应，且设计结果偏于安全。因此，后文将针对Fu et al.(2020)方法进行研究，讨论各个参数对预测结果的影响。

4 Fu et al.(2020)方法的参数分析

4.1 初始剪切模量Gmax

图 6 初始剪切模量Gmax 的影响Fig. 6 Influence of initial shear modulus Gmaxa. L/D=5，H=1200 kN，M=36 000 kN · m; b. L/D=10，H=5000 kN，M=150 000 kN · m

从图6中可以看出，对于Fu et al.(2020)方法，在相同水平荷载作用下，土体初始剪切模量Gmax越大，桩身的水平位移与转角越小。当L/D=10、εc取上下限值时，API方法的预测值分别与Fu et al. (2020)方法及有限元分析采用Gmax/su=100和400时的预测值相近。但当L/D=5时，API方法的预测上限值明显更高。对于刚度较高的土体(例如Gmax/su>400的情况)，有限元结果和Fu et al.(2020)方法预测值均小于API方法的预测下限值。可见，API方法比Fu et al.(2020)方法保守得多，且随着桩基长径比的减小，这一趋势愈加明显。不仅如此，Fu et al. (2020)方法得到的泥面处水平位移和转角与有限元模拟结果更为接近，且能更有效地考虑土体初始模量对桩身水平响应的影响。

4.2 破坏塑性剪应变

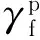
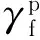
图 7 破坏塑性剪应变的影响Fig. 7 Influence of plastic shear strain on failure a. L/D=5，H=1200 kN，M=36 000 kN · m; b. L/D=10，H=5000 kN，M=150 000 kN · m

4.3 桩土界面粗糙系数α

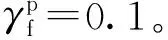
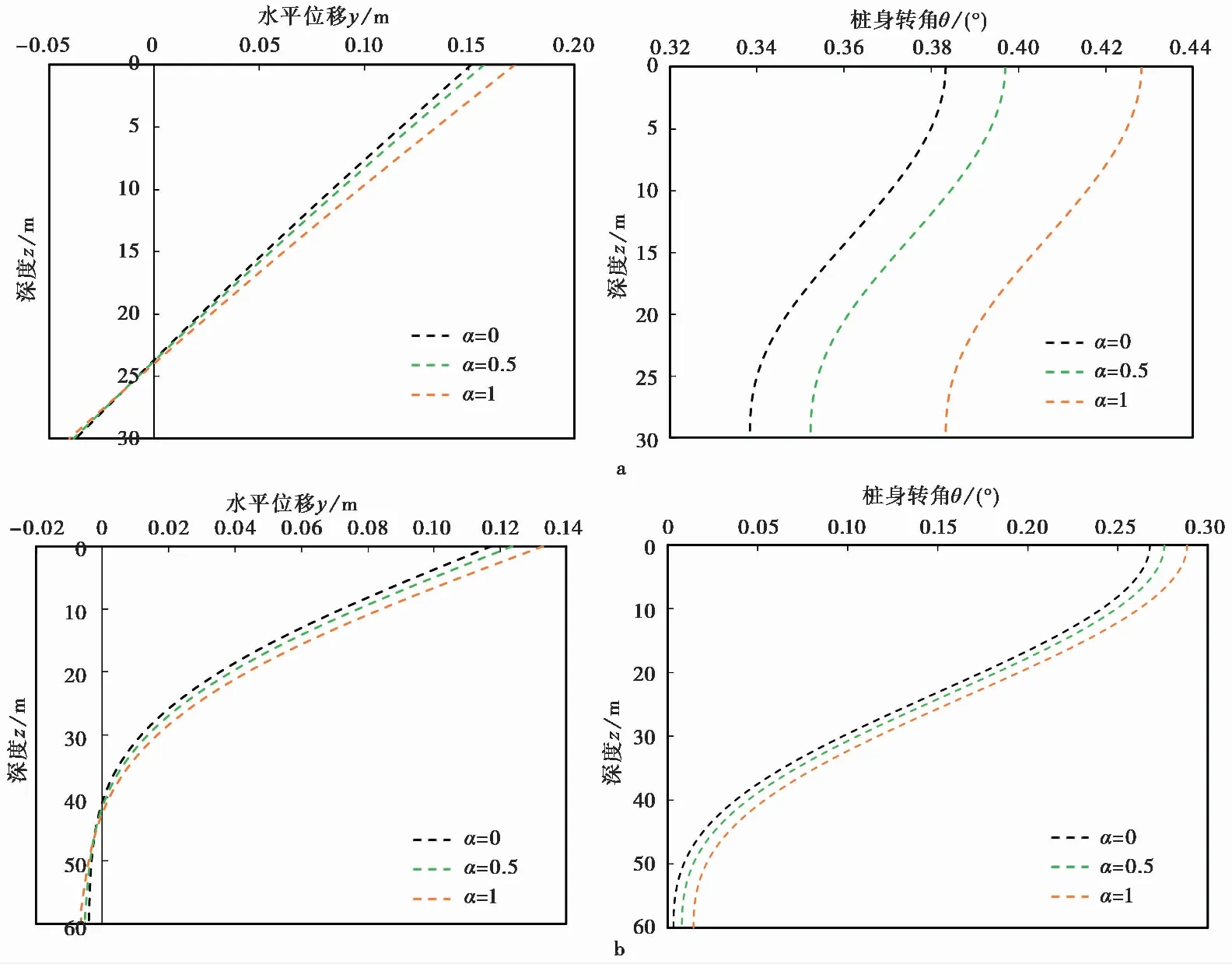
图 8 不同α条件下预测结果的对比Fig. 8 Comparison of prediction results under different αa. L/D=5，H=5000 kN; b. L/D=10，H=10 000 kN

预测结果表明，随着桩土界面粗糙系数α的增大，桩身在水平荷载下产生的位移和转角也相应增大。这是因为在Fu et al.(2020)方法中，对于相同的应力-应变τ-γ曲线，系数α的增大意味着缩放得到的p-y曲线被“拉长”(式3)，桩身水平荷载传递响应变“柔”。需要注意的是，随着系数α的增大，由桩土界面摩擦引起的桩身m-θ旋转弹簧所能够发挥的力矩极限值也将随之增大(式12)。但桩土界面粗糙度对p-y曲线的影响仍占主导作用，因此当粗糙系数从α=0增加到α=1，L/D=5和10时的桩顶位移分别增大约13.5%和13.3%，最大转角分别增大约11.7%和7.7%。可见无论长径比如何，α的取值对桩身位移与转角的预测值都有一定影响。

4.4 与桩身分布力矩有关的缩放系数ξp2

从图9中可以看出，系数ξp2对桩身在水平荷载作用下产生的位移的影响十分有限。对于L/D=5的情况，当ξp2从0.17增加到0.5，泥线处的水平位移和转角仅分别增加约4.8%和5.1%，而当长径比L/D为10时，变化可以忽略不计。由此可见，尽管Fu et al.(2020)方法中建议的ξp2取值范围为1/6～1/2，但当L/D≥10，预测得到的桩身响应几乎不受系数ξp2的影响。

图 9 不同ξp2 条件下预测结果的对比Fig. 9 Comparison of prediction results under different ξp2a. L/D=5，H=5000 kN; b. L/D=10，H=10 000 kN

5 结 论

本文对比了4种分析水平受荷单桩桩身响应的预测方法，包括传统API方法以及新近发展的Zhang et al. (2017b)方法、Wang et al. (2020)方法和Fu et al. (2020)方法，并通过与三维有限元分析结果的比较，探讨了各个方法对大直径单桩的适用性。不同方法预测结果与有限元结果的对比表明，对于大直径单桩水平响应的预测，API方法最为保守，而Wang et al. (2020)方法预测得到的桩身位移和转角最小。综合比较而言，Fu et al. (2020)方法预测结果更为合理，且具备其他方法所不具备的优势。

在上述结论基础上，合理变化Fu et al. (2020)方法中的4个可变参数，讨论了参数对预测结果的影响，得出了以下结论：

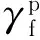
(2)桩土界面粗糙系数对桩身响应有一定影响，α越大，水平受荷桩的桩身水平位移与转角越大，且长径比越小这种影响越显著。

(3)与桩身分布力矩有关的缩放系数ξp2的影响较为有限，当长径比L/D≥10时，其在建议范围0.17～0.5内变化的影响可以忽略不计。