基于优化遗传重采样的辅助粒子滤波检测前跟踪方法

张春景， 柳晓鸣

(大连海事大学，辽宁 大连 116000)

0 引言

检测前跟踪(Track-Before-Detect,TBD)技术可充分利用多帧未进行门限处理的传感器原始数据提高信噪比(SNR)，同时实现对微弱目标的检测和跟踪[1]。粒子滤波(PF)方法[2-4]是一种经典的TBD方法，能有效处理任何线性和非线性系统模型、高斯和非高斯噪声模型，故得到了广泛应用。但粒子退化一直是降低粒子滤波检测前跟踪(Particle Filter Track-Before-Detect,PF-TBD)方法性能的根本原因，研究者们主要通过选取重要性分布函数或改进重采样来解决粒子退化问题，保证了有效粒子数量[5]。

辅助粒子滤波检测前跟踪(Auxiliary Particle Filter Track-Before-Detect,APF-TBD)[6-8]方法在采样前先做重采样，使重采样后的粒子移动到似然函数高值区，较有潜力的粒子被延续到下一时刻，但重采样会使粒子陷入匮乏状态，可通过改进重采样进一步优化该方法。基于优化遗传重采样的粒子滤波检测前跟踪用优化后的遗传重采样代替PF-TBD方法的重采样[9]，一定程度上解决了粒子匮乏问题，但该方法仍然采用状态先验转移分布作为重要性分布函数。文献[10]将正则化思想引入辅助粒子滤波(Auxiliary Particle Filter,APF)的重采样中，在保证粒子有效性的同时，解决了粒子匮乏问题，但只有状态噪声较小时，正则化粒子滤波才能达到较高的滤波精度，可将此改进思想引入APF-TBD方法中。本文提出了基于优化遗传重采样的辅助粒子滤波检测前跟踪(Auxiliary particle filter track-before-detect based on optimized genetic re-sampling,OGRAPF-TBD)方法，在APF-TBD的重采样中应用优化后的遗传重采样算法，保证有效粒子数量的同时，增加了粒子多样性，故OGRAPF-TBD方法具有更稳定的检测跟踪性能。仿真实验验证了本文所提方法的优越性。

1 系统模型

1.1 目标运动模型

假设微弱目标在x-y二维平面内运动，该目标的状态方程可表示为

xk=fk(xk-1+wk)

(1)

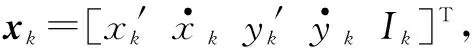
以目标存在变量Ek∈{0,1}表示k时刻目标是否在观测区域内，Ek=1,表示目标存在，Ek=0,表示目标不存在。假设初始时刻目标的存在概率λ=P(E1=1)为已知参数。从Ek-1到Ek的转换被建模成马尔可夫链[11]，即

(2)

式(2)可通过转移概率矩阵描述[11]为

(3)

式中，Pb，Pd和1-Pb分别代表目标的“出生”、“死亡”和“生存”概率。

1.2 雷达观测模型

雷达提供了观测区域的一系列二维图像(单位为帧)，每帧由Nx×Ny个分辨单元组成，Nx和Ny分别代表x轴和y轴上的分辨单元数。每个分辨单元(i,j)是大小为Δx×Δy的矩阵，中心位置为(iΔx,jΔy)，i=1,2,…,Nx，j=1,2,…,Ny。

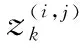
(4)

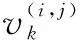
(5)

式中，Σ为已知的模糊参数，表示目标的扩散程度。

分辨单元(i,j)的似然函数为

(6)

式中

(7)

联合似然函数表示为

(8)

实际中，存在的目标只会把强度贡献给其临近的分辨单元，分别用Ci(xk)，Cj(xk)表示被目标影响到的分辨单元的(i,j)标注集合，则似然比为

(9)

式中：Ci(xk)={x0-p,…,x0-1,x0,x0+1,…,x0+p}，预设值p代表分辨单元(i,j)被目标影响的程度，x0代表xk的最大能量单元序号；H1表示假设目标存在；H0表示假设目标不存在。

2 OGRAPF-TBD

2.1 APF算法原理

APF算法由PITT和SHEPHARD提出，通过交换重要性采样和重采样过程将最新量测值考虑到重要性分布函数中。联合密度函数为

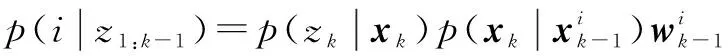
(10)

式中，i为辅助变量。

选择满足以下比例的重要性密度函数

(11)

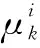
(12)

式中：ij为在k-1时刻预测xk的采样粒子；N代表粒子总数。

综上可知，APF算法的具体步骤如下。

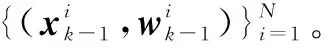
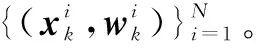
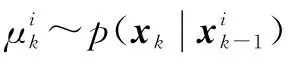
2.2 优化的遗传重采样思想

传统遗传重采样中被选中的粒子可能达不到局部最优点，而且对随机选择的粒子进行交叉操作会降低粒子利用率[9]，优化的遗传重采样主要改进了选择和交叉算子，具体步骤如下所述。

1) 轮盘赌选择：粒子权值就表示粒子适应度，自然选择通过轮盘赌方法和精英选择来模拟，精英选择保证了父代中的最优粒子能被选择到下一代，轮盘赌的具体步骤如文献[12]。

2) 排序分组交叉(交叉概率为Pc)：首先，按粒子适应度对随机被选中的NPc个粒子进行降序排列；在此基础上，将粒子分为高、低适应度粒子集两组；最后，按序号m对粒子进行交叉操作，即

(13)

(14)

3) 变异(变异概率为Pm)：对随机被选中的NPm个粒子进行变异操作，即

(15)

4) 排序选择：从上述产生的(N+NPc+NPm)个粒子中选择N个适应度最高的粒子。

2.3 OGRAPF-TBD原理

结合上述内容，基于优化遗传重采样的辅助粒子滤波检测前跟踪方法的具体步骤如下。

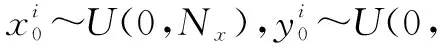
(16)

4) 计算粒子权重并归一化

(17)

8) 判决目标是否存在，即

(18)

9) 若目标存在，估计其状态

(19)

3 仿真验证

为证明OGRAPF-TBD方法在检测跟踪性能上的优势，本文设计了不同低SNR条件下的仿真实验。假设已生成40帧数据序列，每帧由Nx×Ny=50×50个分辨单元组成，每个分辨单元大小Δx×Δy=1×1，雷达扫描时间间隔T=1 s，模糊参数Σ=0.7，目标对分辨单元的影响程度p=3，测量噪声方差σ2=1。目标在第7帧出现，第8～35帧做匀速直线运动，第36帧消失。目标运动模型表示为

xk=F·xk-1+wk

(20)

式中，F为状态转移矩阵，即

(21)

(22)

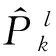
图1所示为进行1000次蒙特卡罗实验后3种方法对目标平均发现概率的估计。

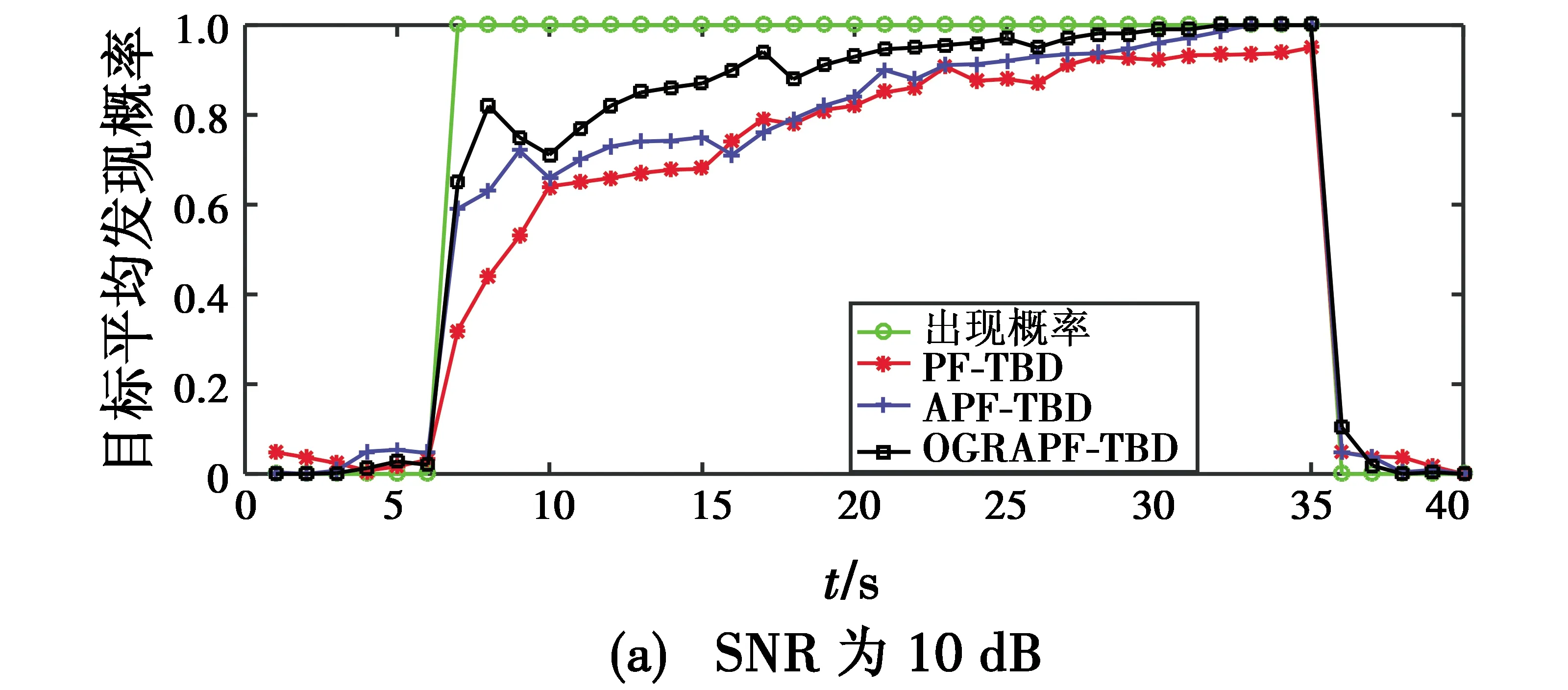
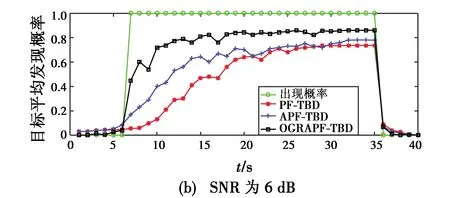
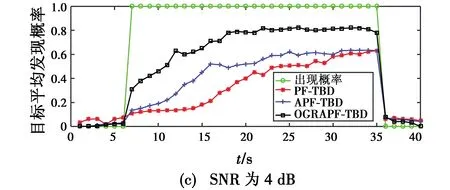
图1 目标平均发现概率估计Fig.1 Estimation of average target detection probability

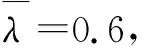
图2为进行1000次蒙特卡罗实验后3种方法对目标位置均方根误差(RMSE)的对比。

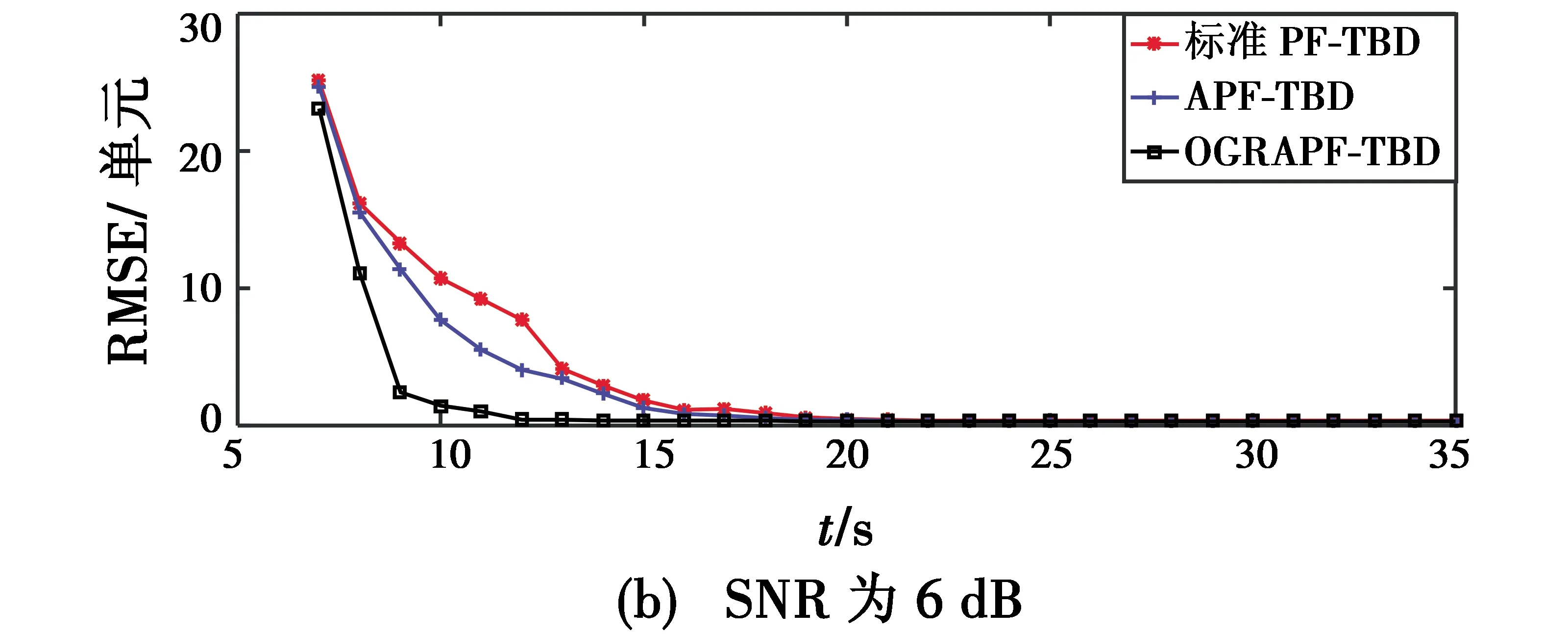
图2 目标位置RMSEFig.2 RMSE of target location

容易发现，SNR一定时，OGRAPF-TBD方法的跟踪精度最高，尤其当SNR分别为6 dB和4 dB时最为明显。之后，随着SNR的下降，3种方法的位置RMSE都在不同程度上增大，但OGRAPF-TBD方法的变化更加稳定，原因是OGRAPF-TBD方法从优化重要性分布函数和改进重采样两个角度保证了粒子的有效性和多样性，说明OGRAPF-TBD方法的适用能力更强。

表1为3种方法在SNR为6 dB时不同粒子总数下总帧数运行时间的比较。

表1 总帧数运行时间Table 1 Running time of total frame number s

很明显，随着粒子数的增加,每种方法总帧数运行时间都在延长；而且，当粒子数一定时，OGRAPF-TBD方法的总帧数运行时间最长，大概是APF-TBD方法的1.3倍，PF-TBD方法的2.267倍，说明本文所提方法是以牺牲总帧数运行时间为代价来优化检测跟踪性能的，原因是优化的遗传重采样中包含两次选择操作并采用了排序分组的交叉操作，比APF-TBD方法和PF-TBD方法中的重采样过程更为复杂。

4 总结

本文为在低SNR条件下更好地检测跟踪目标，提出了OGRAPF-TBD方法。用优化后的遗传重采样代替APF-TBD方法中的重采样，既将当前观测信息引入了重要性分布函数，也对重采样过程进行了改进，保证粒子有效性的前提下，进一步解决了APF-TBD方法的粒子匮乏问题。在不同低SNR条件下进行的仿真实验表明，SNR一定时，OGRAPF-TBD方法具有更高的发现概率和跟踪精度，并且随着SNR的下降，OGRAPF-TBD方法的检测跟踪性能变化更加稳定，适用能力更强。