基于博弈论的高冲突证据融合方法
2022-01-22徐吉辉田文杰史佳辉陈玉金王晓琳
徐吉辉, 田文杰, 史佳辉, 陈玉金, 王晓琳
(空军工程大学装备管理与无人机工程学院,西安 710000)
0 引言
DS证据理论[1-2]是一种可以有效融合多源信息的不确定推理方法,目前被广泛应用于风险评估[3]、方案决策[4]、故障诊断[5]、状态评估[6]等领域。但传统证据理论在融合高冲突证据时,往往会导致悖论问题,因此国内外许多专家学者都对其进行了改进[7-15]。其中,修改证据源的方法保留了经典Dempster组合规则的交换律和结合律,便于进行复杂的合成运算。因此,本文的研究重点放在证据源的预处理上。
YAGER[7]通过对合成公式进行改进来解决高冲突证据问题;孙全等[8]通过引入证据可信度概念对证据合成公式进行改进,弥补了传统DS证据理论和Yager合成公式的不足;MURPHY[9]平均赋予每条证据相同的权值,解决了证据间的冲突问题;文献[10-11]用Joussleme距离来衡量证据间的冲突程度,确定每条证据源的修正权重,提供了新的解决思路;张欢等[12]使用皮尔逊相关系数衡量证据间的相似度来确定权重,也取得了一定的效果;文献[13-15]通过证据综合不确定度和相似度来计算证据的修正权重系数,对于修正证据源的考虑更加全面。但上述研究存在着以下不足:淡化了冲突证据的存在价值,在进行多证据融合时效果并不理想;忽略了证据间的关联关系和自身不确定性对融合结果的综合影响;虽然考虑到证据综合不确定度和相似度对证据结果的影响,但并未有效组合。
针对上述问题,本文深入分析了4种典型的悖论问题;求解证据综合不确定度和相似度,基于博弈论对两者进行有效组合,以确定其修正权重系数,据此修正原始证据,最后使用传统DS证据组合规则进行证据融合;通过冲突证据融合对比分析、多证据融合对比分析、相似方法对比分析等3个方面与其他方法进行比较。由此发现,所提改进证据理论考虑问题更加全面,在处理冲突问题上精度更高、识别速度更快。
1 传统DS证据理论及其存在的缺陷
1.1 DS证据理论算法
在证据理论中,设Θ为识别框架,识别框架Θ中的子集两两相互排斥,包含Θ的全部识别对象,通常用2Θ表示。∀A⊆Θ,若函数m:2Θ→[0,1],满足
m(∅)=0
(1)
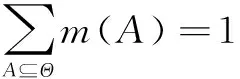
(2)
式中:∅为空集;函数m为Θ上的基本概率分配(BPA);m(A)表示证据对命题A的信任程度,若m(A)>0,称A为识别框架Θ上的焦元。
对于∀A⊆Θ,有限个m1,m2,…,mn在识别框架Θ上,DS证据理论合成规则为
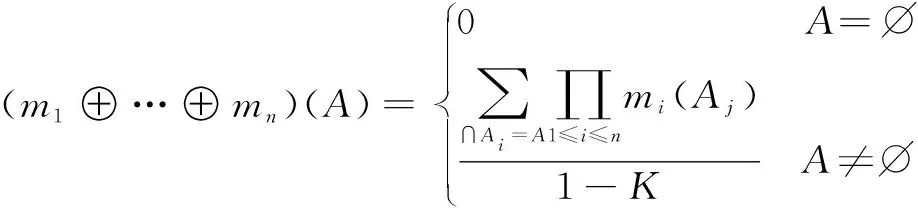
(3)
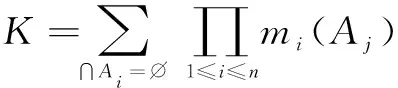
(4)
式中:Aj表示第j个命题;Ai表示包含命题A的集合;K为冲突因子,表征证据间的冲突度,K越大,表明证据间的冲突越大。
1.2 DS证据理论的缺陷问题及分析
通常情况下,传统DS证据理论在信息融合方面能够取得良好的效果,但面临高冲突证据时,得到的结果可能会与常理不同。常见的高冲突证据及其BPA与DS融合结果如表1所示,包括完全冲突、0置信冲突、1置信冲突、极度冲突。
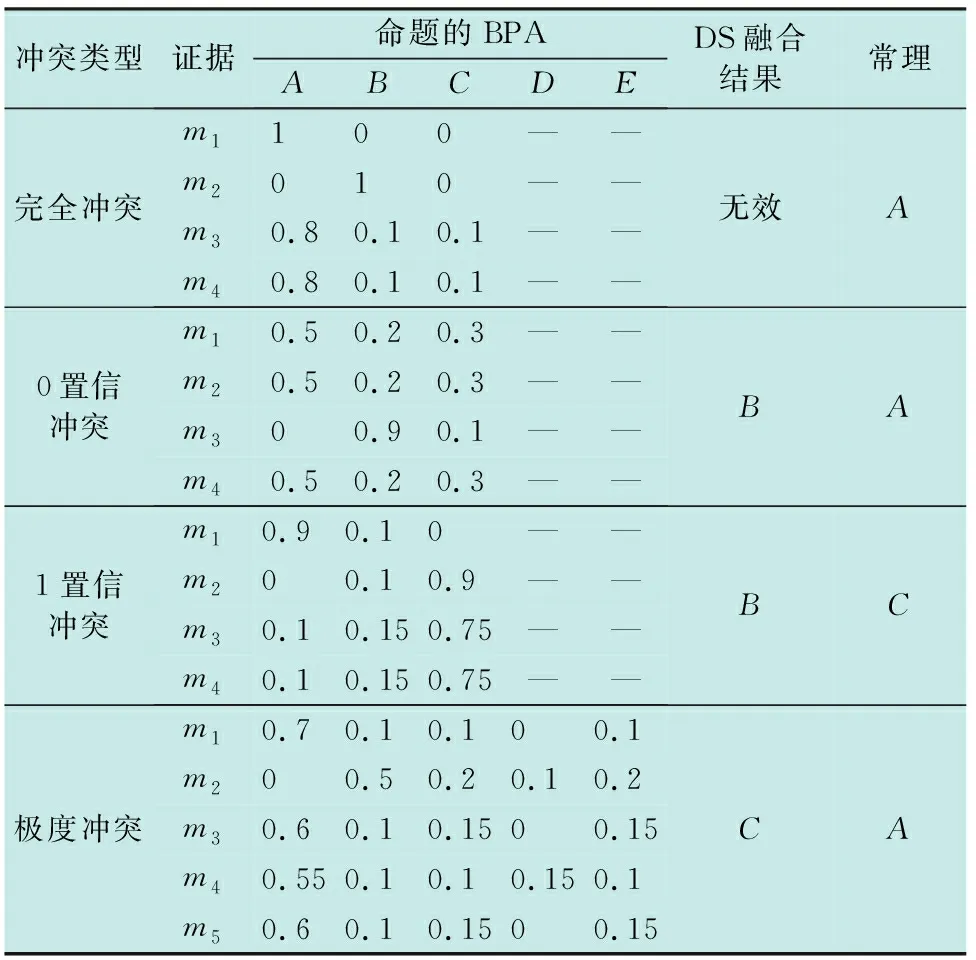
表1 常见高冲突证据Table 1 Common high-conflict evidence
完全冲突:通过式(4)计算可得1-K=0,即分母为0,无法进行融合,所以DS融合规则无效。
0置信冲突:m3(A)=0,说明证据m3对命题A完全否定,即使证据m1,m2,m4支持命题A,但在证据融合后仍然m(A)=0,与常理为命题A不符,所以融合失败。
1置信冲突:因为m2(A)=0,m1(C)=0,导致所有的概率指向全都为命题B,与常理为命题C不符,所以融合失败。
极度冲突:虽然大多证据支持命题A,但m2(A)=0,又因为m1(D)=m3(D)=m5(D)=0,使用传统DS融合规则得到概率指向为命题C,与常理为命题A不符。
针对上述高冲突的证据悖论问题,本文从证据源预处理出发,通过权重系数对证据源进行修正,保留传统的DS证据融合规则,以确保改进DS证据理论的完好性。
2 基于博弈论的改进DS证据理论
通过计算证据的可信度权重和证据间的相似权重,基于博弈论进行组合赋权,目的是对证据的综合不确定度和相似度进行优化协调,从而降低证据自身的随机性和不具体性,以及证据间的冲突性对计算结果的单一影响,确保两者间的一致,使修正证据在融合后更有利于做出正确决策。
2.1 基于类哈利熵和Shannon熵的可信度权重确定
在证据理论中,可以用不具体性和随机性描述证据的综合不确定度[16]。证据的不具体性V(m)可用类哈利熵[17]描述,具体表达形式为
(5)
式中,|A|表示命题A中元素的个数,当命题中只有1个元素时,V(m)=0,说明证据中无不具体性。
证据的随机性S(m)可用Shannon熵[18]描述,具体表达式为
(6)
式中,|A∩B|表示命题A,B中相同元素的个数。
证据的综合不确定度T(m)为不具体性和随机性之和,则
T(m)=V(m)+S(m)=
(7)
当T(m)为0时,为方便计算,保证可信度权值的准确性,令T(m)=0.001。
综上可得,基于综合不确定度的可信度权重系数为
(8)
2.2 基于皮尔逊相关系数的相似度权重确定
在同一识别框架Θ中,证据间存在的相似关系必然会导致计算结果的不精确。本文基于皮尔逊相关系数计算证据间的相似度,确定其相似度权重系数以保证结果的准确性。计算流程如下。
1) 计算证据相关程度。根据皮尔逊相关系数计算两两证据间的相关性,以计算证据mi和mj的相关性si j为例,算式为
(9)
式中,E为数学期望。
2) 建立相关性矩阵S。S由两两证据的相关系数构成,可表示为
(10)
由于si j∈[-1,1],si j≤0时表明两证据负相关,为保证权值计算的准确性,以及降低高冲突证据的影响,本文将si j≤0的结果统一赋值为0.001。
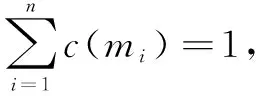
(11)
2.3 基于博弈论的组合赋权
基于博弈论的组合赋权[19],即极小化最优权重与各个权重之间的偏差,寻找最满意的权重向量,保证修正证据的科学合理。计算流程如下。
1) 构造赋权模型。假设有L种赋权方法对证据进行赋权,构造基础权重向量集
ωk={ωk1,ωk2,…,ωkn}k=1,2,…,L
(12)
可得最优权重向量为
ω*=λωΤ
(13)

2) 确定线性方程组。对权重向量进行最优线性组合,旨在保证ωk和ω之间的离差最小,即min‖ω-ωk‖2。
由此可知,基于博弈论的组合赋权构造的求解模型较为简洁,可以归结为一组包含有多个目标函数的交叉规划模型,进行求解计算得到的综合权重,能够达到多种权重赋值方法在整体上的相互协调、均衡一致的效果。
根据微分原理对min‖ω-ωk‖2进行求导,可得
(14)
3) 计算组合权重系数。由式(14)可求得线性组合系数λ=(λ1,λ2,…,λL),对其进行归一化,可得
(15)
由式(15)可得最优权重向量为
(16)
由式(16)可得修正证据为
m(Ai)=ω*m(Ai)T
(17)
式中,m(Ai)=(m1(Ai),m2(Ai),…,mn(Ai))。
3 算例分析
为验证本文提出方法的有效性,从高冲突证据融合、多证据融合、相似方法对比这3个方面进行分析比较。
3.1 高冲突证据融合对比分析
针对1.2节所提出的4种常见高冲突证据类型,本文选择传统DS证据理论、文献[9]、文献[10]及文献[12]方法与本文方法进行证据融合对比分析,计算结果见表2。
由表2可知,本文在处理完全冲突、1置信冲突、极度冲突证据融合问题上结果均与常理一致,对于这3种冲突皆有效。在处理0置信冲突时,m(B)>m(A)且两者相近,融合结果与常理不同,现分析如下:本文相对于其他方法考虑的角度更加全面,从证据自身的综合不确定度和证据之间的相似度出发,对两者进行有效组合,解决了相似度单一影响证据结果的问题。在0置信冲突中,证据m1,m2,m3,m4的综合不确定度T(m)、可信度权重系数αi、相似度权重系数βi及综合权重系数ω*如表3所示。
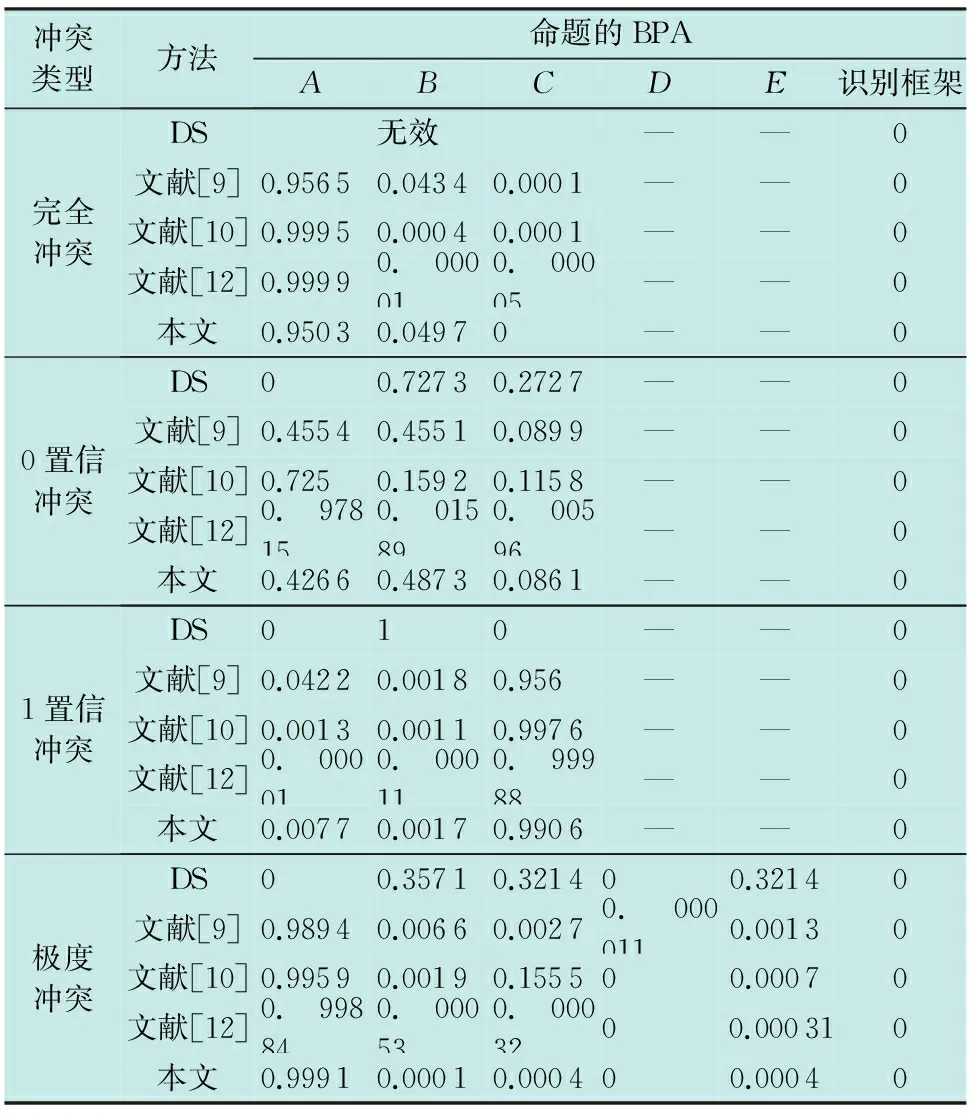
表2 高冲突证据融合结果Table 2 Results of conflict evidence fusion
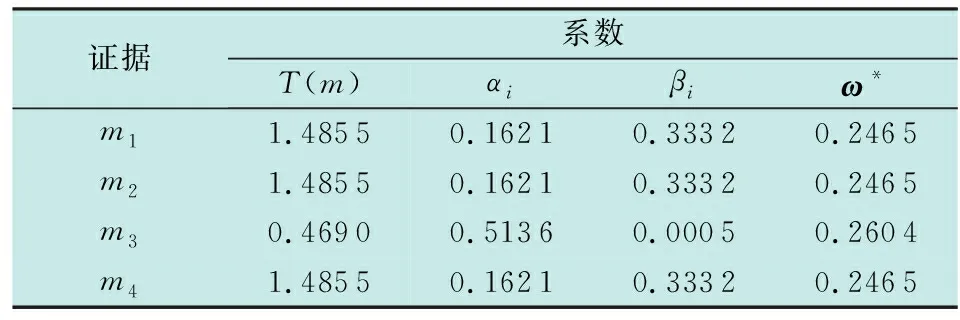
表3 0置信冲突中证据的权重Table 3 The weight of evidence in 0 confidence conflict
由表3可知,证据m3中仅含有2个焦元,而其他证据中有3个焦元,根据熵增原理,焦元越多,越混乱,因此,证据m3的综合不确定度较小。通过式(8)计算可得证据m3的可信度远大于证据m1,m2,m4。经过皮尔逊相关系数计算可发现,m3的相似度与其他证据的相似度差别较大。本文基于博弈的思想,通过式(17)计算证据的综合权重系数,可得证据m3的权重系数稍大。经过证据融合得m(B)略大于m(A)。对于完全冲突存在命题为0、但融合结果却可以指向常理命题的现象,主要是证据m1,m2可信度权重高,证据m1,m3,m4相似度远大于m2,导致证据m1综合权重极大,因此融合结果为命题A。同理可得,1置信冲突和极度冲突在证据融合后能指向常理命题。
究其原因,本文算法从每条证据皆合理的原则出发,保留证据的独立性、相关性和客观性。与其他方法相比,虽然对常理证据的概率分配偏小,但降低了BPA的敏感性,避免了相似度对证据融合的单一影响,提高了证据融合的鲁棒性。
3.2 多证据融合对比分析
多证据融合结果的合理性是衡量改进方法有效性的重要因素。为检验本文算法多证据融合的有效性,选择证据m1为0.5,0.2,0.3,m2为0,0.9,0.1,m3为0.55,0.1,0.35,m4为0.55,0.1,0.35,m5为0.55,0.1,0.35,与传统DS证据理论、文献[7-9]方法进行对比分析,分为4组进行实验,融合结果的常理命题BPA如表4所示。
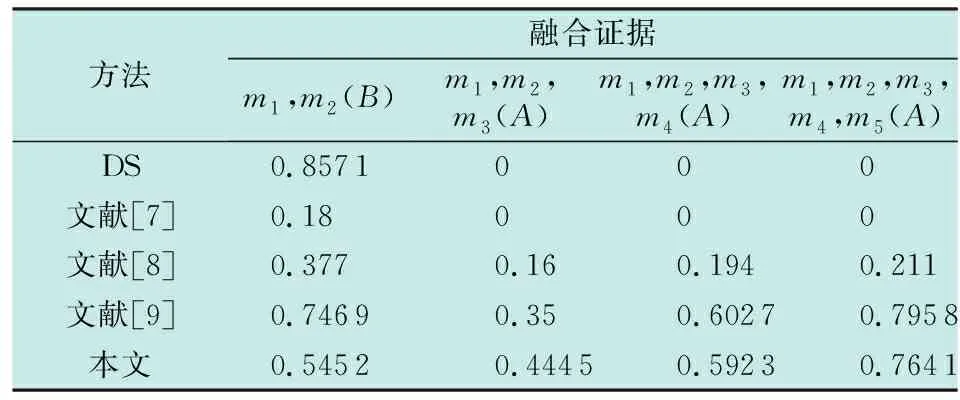
表4 常理命题BPATable 4 BPA for common sense propositions
对于传统DS方法,0置信问题导致m(A)=0恒成立,在应用中显然不符合实际。同时,文献[7]也没有解决此类问题,将冲突证据归入未知邻域中,本质上无法摆脱传统DS证据理论的“一票否决”问题,尤其在处理两个证据以上的问题时往往是失效的,因此在实际应用时也不予考虑。文献[8]在文献[7]的基础上引入可信度概念,虽然解决了“一票否决”问题,但并不能有效指向常理命题。文献[9]对证据进行平均再融合,虽然可以判断出与常理相同的结果且效果稍好,但丧失了证据间的关联性,同时没有相关理论做支撑,比较适合处理较为相似的证据,因此在本文实验中有一定优势。为更加直观地进行比较分析,常理命题BPA如图1所示。
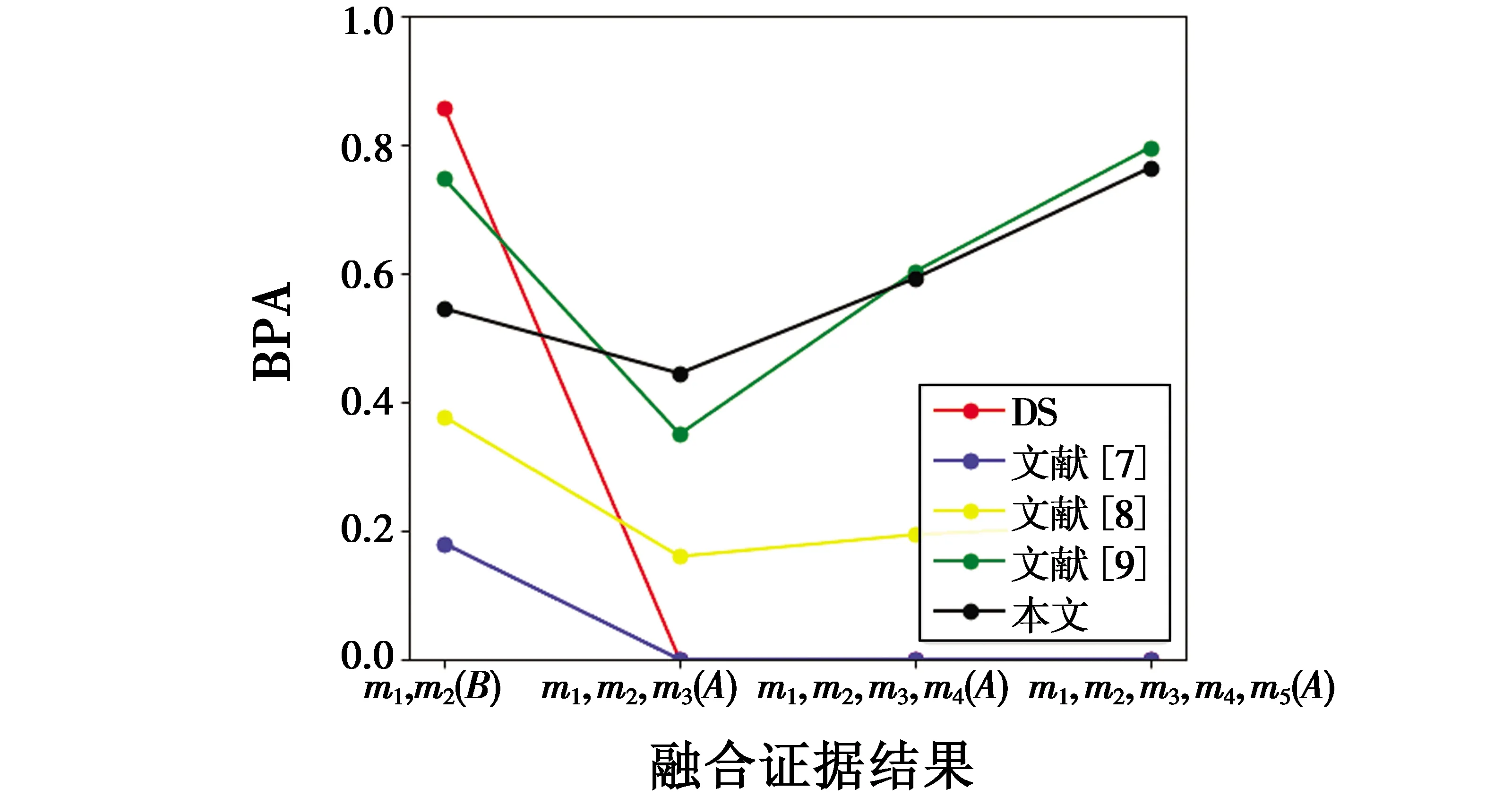
图1 常理命题比较Fig.1 Common sense proposition comparison
实验中,本文方法虽然在两证据融合时效果稍差,但仍能指向常理命题,且与其他方法相比,在后续几组多证据实验中,识别常理命题的速度更快,其概率指向都处于较高的水平。由此说明,本文方法在处理多证据融合问题时更具有一定的优越性。
3.3 相似方法对比分析
文献[13-15]也考虑到从证据自身不确定度和证据间的相似度进行赋权来改进证据理论。为验证本文方法的有效性,与文献[13-15]方法进行比较分析,选择文献[13]的数据作为实验数据,如下:m1(A)=0.41,m1(B)=0.29,m1(C)=0.3;m2(A)=0,m2(B)=0.9,m2(C)=0.1;m3(A)=0.58,m3(B)=0.07,m3(A,C)=0.35;m4(A)=0.55,m4(B)=0.1,m4(A,C)=0.35;m5(A)=0.6,m5(B)=0.1,m5(A,C)=0.3。
对以上5个证据体进行融合,分为4组进行实验,计算结果见表5。
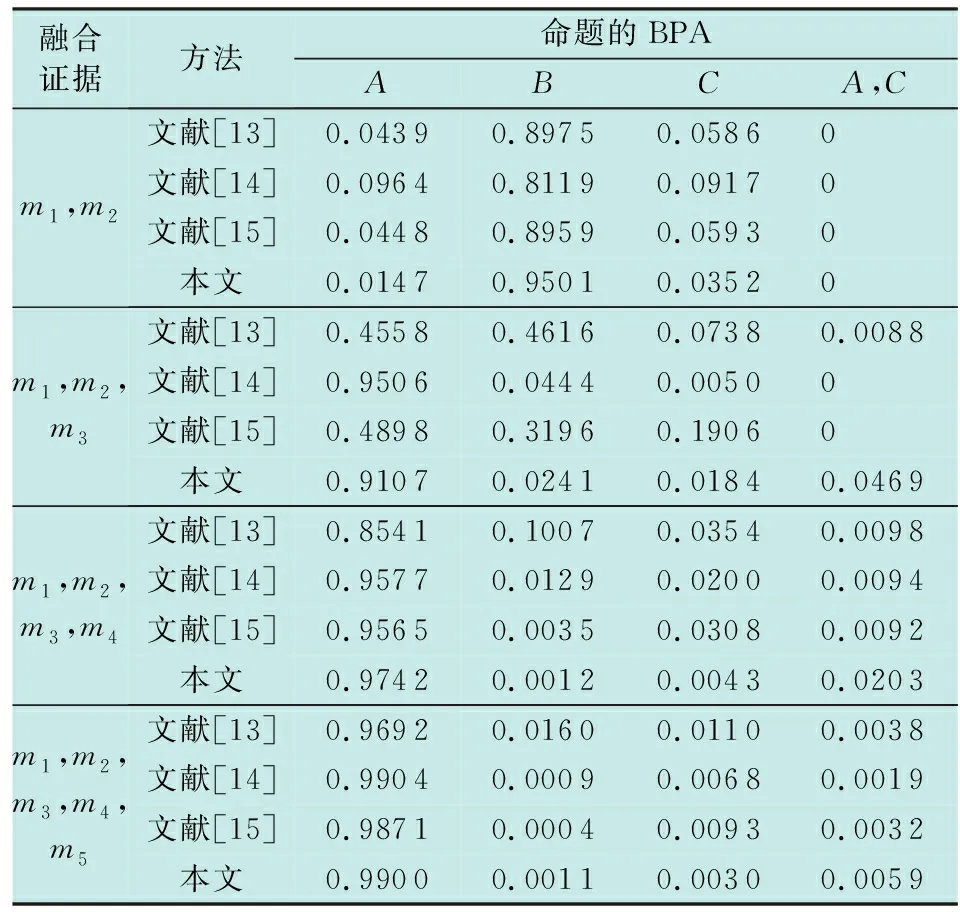
表5 多证据融合的BPA比较Table 5 Comparsion of BPA in multiple evidence fusion
由表5可知,4组实验进行证据融合,所得最大概率指向分别为B,A,A,A,与常理保持一致,说明本文方法对以上4种组合均有效。
文献[13]虽综合考虑证据不确定度和证据间相似度,但仅对两者进行平均赋权,没有考虑到针对不同情况二者权重系数并不相同的问题,不符合客观实际,因此结果最差;文献[15]则以证据是否相似为前提判断证据是否可信,再进行不确定度的计算以确定权重分配,二者并未处于一种并列的关系,导致相似度高的证据赋予的权重较高,实验取得效果并不理想;文献[14]方法思路与文献[15]相同,因为采用的信度熵方法衡量不确定度具有一定的优势,所以实验取得的效果优于文献[13,15];本文方法则以证据自身不确定度和证据之间相似度处于一种并列关系为前提,基于博弈论进行组合赋权,常理命题BPA高于其他方法,同时,识别常理命题的速度远超于其他方法,能极大地降低识别结果的不确定性。图2可以反映出本文方法效果更加显著。
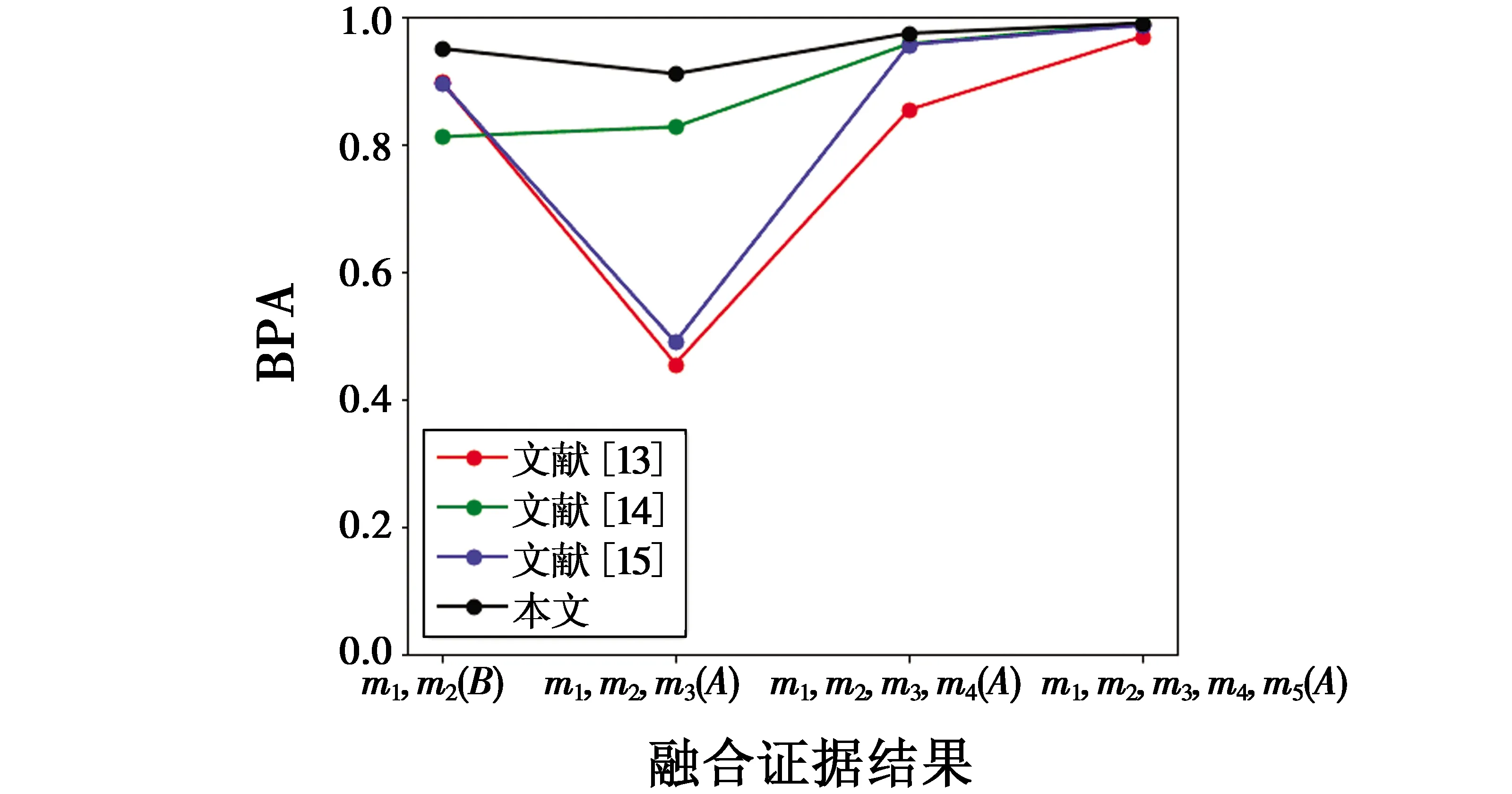
图2 相似方法的常理命题BPAFig.2 Common sense proposition BPA for similar methods
4 结束语
当高冲突证据融合时,传统DS证据理论无法做出合理判断。针对这一问题,本文从修正证据体权重的角度出发对证据理论进行改进,得到一种新的证据理论算法,特点如下。
1) 解决了修正证据考虑不全面的问题。以随机性、不具体性描述证据不确定度,同时考虑到证据相似度的影响,使用二者对证据进行修正,使计算结果更加贴合实际。
2) 对证据进行合理组合赋权。在组合权重的过程中引入博弈论,降低基于证据不确定度赋权的随意性和基于相似度赋权的绝对性,所得改进的修正权重更加合理有效。
3) 提高了识别常理命题的速度及准确性。通过改进证据理论能够对有效信息进行融合,提高融合信息精度,又可以使融合后各命题的BPA快速收敛,降低信息融合过程中的不确定性,有利于进行快速决策。
4) 可以广泛应用于工程实践。进行专家决策时,由于专家的可信赖程度不同,当意见不一时,往往无法合理赋权,通过改进证据理论可以科学地融合专家信息,保证最终决策结果的合理性。
