120阶群的完全分类

陈松良，石昌梅，欧阳建新，莫贵圈

120阶群的完全分类

陈松良，石昌梅，欧阳建新，莫贵圈

（贵州师范学院 数学与计算机科学学院，贵州 贵阳 550018）

设是120阶群，证明了共有47个互不同构的类型，其中Sylow5-子群正规的群有44个，而Sylow5-子群不正规的群有3个。

有限群；同构分类；群的构造

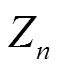
1 主要结果

定理1120阶群共有47个互不同构的类型，其中Sylow 5-子群为正规子群的有44个不同构的类型，Sylow 5-子群为不正规子群的有3个不同构的类型。

2 定理1的证明

定理1的证明需要下面的引理。

引理1设是24阶群，则必同构于下列15种类型之一[1]：

引理2如果是5-子群不正规的60阶群，那么必同构于5次交错群5。

证明 见文献[4]之推论1。

注1 文献[4]中引理2的证明过程不完整，遗漏了以下两种构造：

因此，当Sylow 5-子群正规时，60阶群恰有12个互不同构的类型，加上Sylow 5-子群不正规的60阶群只有一个，故60阶群总共有13个互不同构的类型。

以下恒设是120阶群，是的Sylow 5-子群。

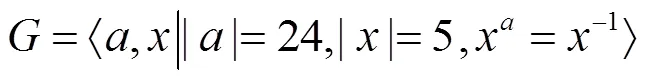
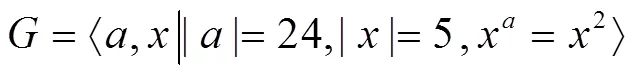
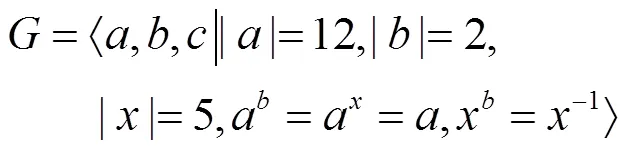
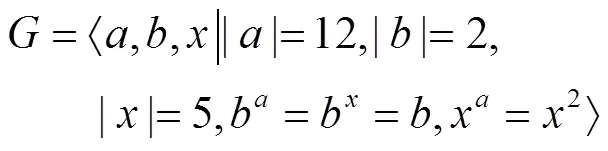
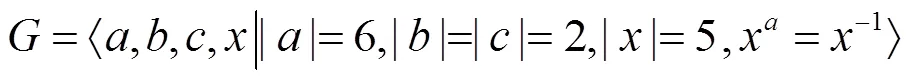
与(6)是同构的。

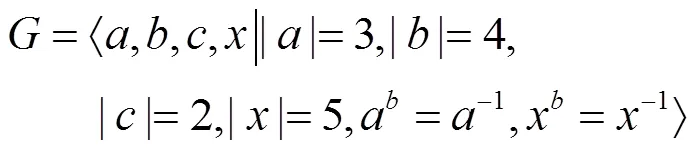
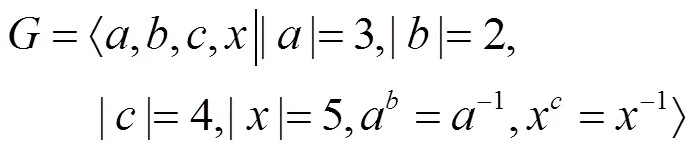
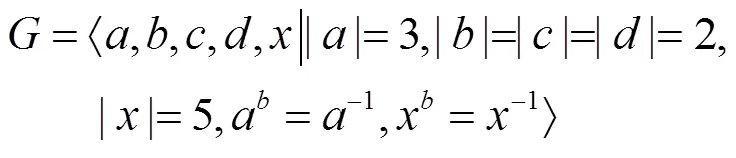
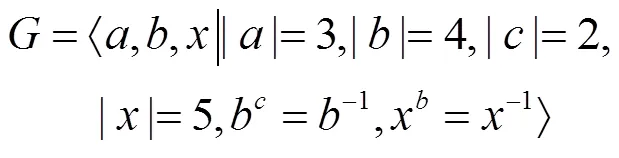
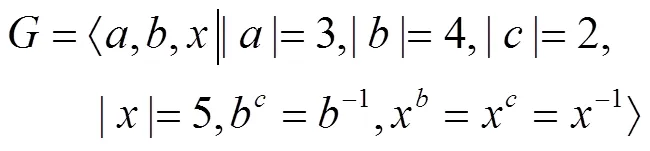
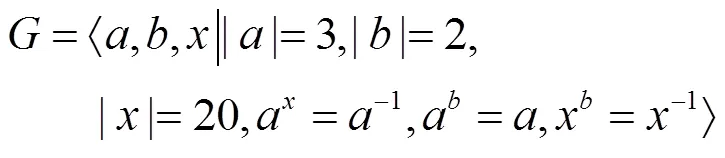
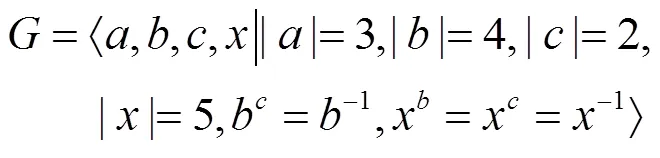
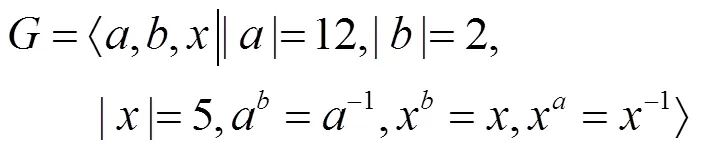
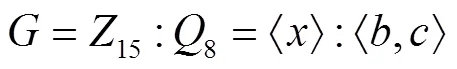
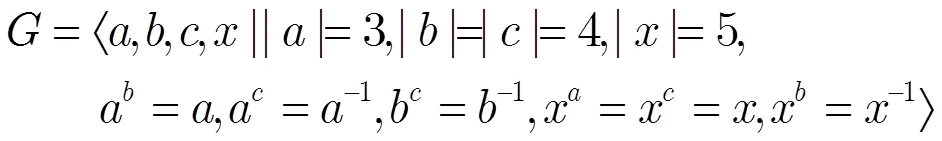
但上述构造中，若将，分别记为与，则可知它与(27)是同构的。

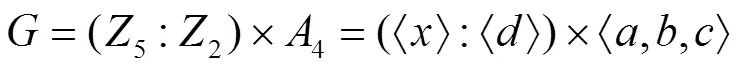
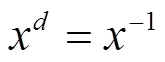
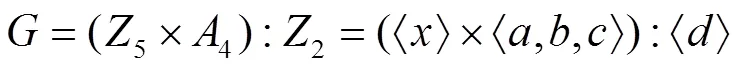
其中

引理3证毕。

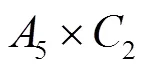
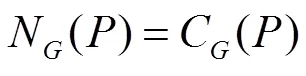
如果没有2阶正规子群，那么是不可解的。考虑的置换表示

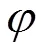
由引理3和引理4可知，定理1成立。

[1] 陈松良,欧阳建新,李惊雷.3阶群的完全分类[J].海南师范大学学报(自然科学版),2010,23(3):253-255.

[2] 陈松良.论p3q2阶群的构造[J].华中师范大学学报(自然科学版),2016,50(3):321-325.

[3] 陈松良,黎先华.33阶群的完全分类[J].吉林大学学报(理学版),2018,56(4):793-796.

[4] 陈松良,欧阳建新,李惊雷.论60阶群的构造[J].唐山师范学院学报,2012,34(2):22-24.

[5] 陈松良,蒋启燕.关于83阶群的一个注记[J].唐山师范学院学报,2016,38(2):1-4.

[6] 徐明曜.有限群导引(上册)[M].北京:科学出版社,1999.

[7] Robinson D J S. A course in the theory of groups[M]. Berlin: Springer-Verlag, 1982.

[8] Kurzweil H, Stellmacher B. The Theory of Finite Groups [M]. New York: Springer-Verlag, 2004.

Complete Classification of Groups with Order 120

CHEN Song-liang, SHI Chang-mei, OUYANG Jian-xin, MO Gui-quan

(School of Mathematics and Big Data, Guizhou Education University, Guiyang 550018, China)

Whenis a group of order 120 it was proved thathas 47 nonisomorphic structures. If its Sylow 5-subgroups are normal, it has 44 nonisomorphic structures. If its Sylow 5-subgroups are non-normal, it has 3 nonisomorphic structures.

finite group; isomorphic classification; structure of group

O152.1

A

1009-9115(2021)06-0003-04

10.3969/j.issn.1009-9115.2021.06.002

国家自然科学基金项目（11661023），贵州省科技计划资助项目（黔科合基础[2017]1136），贵州省省级重点学科（ZDXK[2018]007号）

2021-01-19

2021-11-08

陈松良（1964-），男，湖南双峰人，博士，教授，研究方向为代数学及其应用。

（责任编辑、校对：赵光峰）