我国信用风险缓释凭证定价模型研究

2022-01-21郑德渊温乃馨

会计之友 2022年3期

郑德渊温乃馨

【关键词】信用风险缓释工具; 结构模型; 资产变现率

【中图分类号】 F234.3;F830.91 【文献标识码】 A 【文章编号】 1004-5937（2022）03-0016-07

一、引言

2010年10月，中国银行间市场交易商协会发布《银行间市场信用风险缓释工具试点业务指引》，我国信用衍生品发展正式启动。2016年，《银行间市场信用风险缓释工具试点业务规则》及《中国场外信用衍生产品交易基本术语与使用规则》相继出台，进一步规范我国信用衍生品市场的发展。我国信用缓释工具体系包括：信用风险缓释凭证（Credit Risk Mitigation Warrant，CRMW）、信用风险缓释合约（Credit Risk Mitigation Agreement，CRMA）、信用违约互换（Credit Default Swap，CDS）、信用联结票据（Credit-Linked Notes，CLN）。

我国市场上发行的信用衍生产品主要是信用风险缓释凭证。Wind资讯数据显示：2018年发行CRMW产品50单，名义本金64.25亿元，参考实体35家，标的债券46只;2019年发行CRMW产品91单，名义本金100.57亿元，参考实体62家，标的债券91只;截至2020年9月共有55家CRMW创设机构。鉴于此，本文针对该类产品展开研究。

我国信用风险缓释凭证产品的条款、交易方式及流动性与成熟市场信用衍生品存在明显差异[ 1 ]，直接应用成熟市场上的信用衍生品定价模型必然存在较大误差，建立适应中国缓释凭证条款特征的定价模型，既有理论价值也有实践意义。相对精准的定价模型有助于投资者准确判断投资价值，有助于凭证发行机构和中介机构合理确定公允价值，也有助于监管机构制定相应的监管政策和指导意见。

本文的学术贡献包括三个方面：第一，以KMV模型为基础，以资产不足以偿还全部债务测度破产违约概率，以资产可变现价值低于短期有息负债测度支付违约概率，综合考虑破产违约和支付违约两类信用事件，得到符合产品条款特征的缓释凭证定价模型;第二，以公司资产价值服从几何布朗运动为前提，通过引入时变变现率参数，运用伊藤定理得到资产可变现价值变动过程，并基于此假设计算支付违约概率，克服了传统财务指标仅能静态衡量公司支付违约风险的弊端;第三，选择2018—2020年间作为缓释凭证参考实体出现最为频繁的红狮控股为对象，利用公司资产负债表财务数据和相关市场交易数据，估计挂钩该公司超短期融资券的缓释凭证的理论价格，比较模型计算结果差异，分析差异产生原因，确定应用模型过程中应当重点关注的参数，提供切实可行的模型应用方案。

二、文献综述

（一）国外信用衍生品定价模型研究

国外信用衍生品定价模型分为三类：第一类是结构模型[ 2 ]。该类模型通常假定公司价值服从几何布朗运动，将长期债务以一定比例折算后与短期债务加总作为违约点，利用期权理论，从可观测的股票价值及股票波动率信息中倒推出資产价值及资产波动率，进一步得到破产违约距离和破产违约概率，以违约概率为基础可得信用衍生品的理论价格。结构模型广泛应用于我国商业银行[ 3 ]、房地产企业[ 4 ]、上市公司[ 5 ]及地方政府[ 6 ]债务信用风险度量中，并以其较好的信用风险预测能力被理论界和实务界广泛认可。本文针对破产违约概率和支付违约概率的研究，以KMV这一典型结构模型为基础展开。

第二类是简约模型[ 7 ]。该类模型未对公司资产价值变动过程做任何假定，也未考虑违约发生内在机制，而是直接以外生的泊松过程刻画公司破产违约事件变动规律，以此预测未来特定时间间隔内破产违约概率，进而确定信用衍生品价格。本文未直接采用简约模型计量破产违约和支付违约概率，但借鉴简约模型的思路，参照我国债券违约历史数据信息，以外生方式确定信用事件发生时债券投资者的现金回收比例。因此本文建立的信用缓释凭证定价模型是一类兼具结构模型和简约模型特征的混合模型。

第三类是信用利差模型[ 8 ]。该类模型通过建立信用利差曲线、分析信用利差波动率和信用利差相关系数来确定信用衍生品价值。此类模型的研究成果与本文模型关联程度较弱。

（二）国内信用衍生品定价模型研究

我国学者针对信用衍生品定价模型展开一系列研究。雎岚和施虓文[ 9 ]、张强和吴敏[ 10 ]、任达和赵倩倩[ 11 ]分别运用简约模型构建我国信用风险缓释工具定价模型，选取当时市场流通的CRMW产品对定价模型的合理性和有效性进行实例验证和应用分析，并提出相应政策建议。雎岚和施虓文[ 9 ]采用蒙特卡洛模拟法估计债券现金回收率，并将凭证购买方违约风险考虑在模型中，张强和吴敏[ 10 ]、任达和赵倩倩[ 11 ]利用债券收益率曲线估计违约强度，这三篇文献均将破产违约与支付违约信用事件统一处理，模糊了两类信用风险的差异。扈文秀和李茹霞[ 12 ]运用混合模型思路构建我国CRMW产品定价模型，采用蒙特卡洛模拟方法估计挂钩我国地方政府债的CRMW产品价格，该模型的构建思路与本文最为接近，但两类模型所研究的产品类型不同，考虑的信用事件类型各异，测度违约概率的方法也不一样。

三、模型建立

（一）基本框架

我国信用风险缓释凭证产品通常采取起始日付费、到期日实物交割方式，凭证挂钩标的债券为单一短期债券，且凭证必须与标的债券捆绑销售，不能裸买，凭证条款规定的信用事件为参考实体发生破产、支付违约、债务加速到期、债务违约和偿付变更。目前已发行的凭证产品多以发生破产违约、支付违约作为缓释凭证标的信用事件，本文重点围绕这两类违约风险展开。

按照缓释凭证标准合同文本规定，破产违约包括参考实体解散、不能清偿到期债务且资产不足以清偿全部债务或明显缺乏清偿能力、书面承认其无力偿还到期债务等九种类型，支付违约指参考实体未按约定在标的债务的付息日和本金兑付日足额履行支付义务，未支付款项总金额超过适用的起点金额，且在适用的宽限期届满时仍未纠正①。考虑到相关指标的可量化程度，本文将破产违约限定为公司资产不足以偿还公司总体债务情形，其发生概率为破产违约概率，对应的违约距离为破产违约距离。以公司资产可变现价值低于短期有息负债余额度量支付违约信用事件，其发生概率为支付违约概率，对应的违约距离为支付违约距离。

按照凭证条款设计与安排，凭证到期日与标的债券到期日相同。到期日信用事件发生时，凭证买方将所持公司债券转让给凭证卖方，凭证卖方将到期日债券本金和利息支付给凭证买方。到期日信用事件未发生时，凭证买卖双方没有现金流交换，凭证丧失保护作用。

因此，缓释凭证到期日？子时凭证购买方的现金流结构为：

其中：CRMW？子表示到期日凭证现金流，W？子表示凭证到期日参考实体资产价值，B？子表示到期日参考实体应偿还债务余额，B1？子表示到期日参考实体应偿短期有息负债，B1？子为债务余额的一部分，到期日标的债券面值与利息支付金额之和为F？子+I？子。参数？子表示到期日？子时的资产变现率，指到期日公司资产中可以直接变现的比例。参数？茁为现金回收率，表示信用事件发生时债券持有人回收现金金额占应回收债券本金和利息金额的比例，其值介于0～1之间，？茁=1表示凭证发行人全额偿付投资者，？茁=0表示发行人未做任何偿付。

当W？子≥B？子时，？子时资产价值高于应偿还债务余额，参考实体不发生破产违约，以P 表示估值日t时估计的？子时参考实体不发生破产的概率。当 *W？子≥B1？子时，？子时资产可变现价值高于应偿还短期有息负债，参考实体不发生支付违约，以P 表示估值日t时估计的到期日参考实体不发生支付违约的概率。以P 表示估值日t时估计的到期日信用事件不发生的概率，P =min（P ，P ），其中min（x，y）为x值和y值间取最小值的函数，相应地信用事件发生的概率为1-P =1-min（P ，P ）。

估值日t时，信用风险缓释凭证的理论价值为：

其中：CRMWt表示估值日凭证理论价值，PV（）为贴现率函数，贴现率取自与标的债券具有相同信用评级债券的收益率曲线。

（二）破产违约概率

破产违约概率计算分两个步骤：第一步以KMV模型為基础估计资产价值、资产价值增长率及其波动率;第二步利用前步估计结果，计算缓释凭证到期日公司发生破产违约的概率。

KMV模型将估值日股票市场价值Et视为看涨期权，期权执行价格为公司账面债务价值BT，债务集中于未来某一时点T到期，通常设为T=1，以公司最近一个资产负债表日“短期负债+1/2*长期负债”作为BT的近似。到期日T时，期权收益结构为：

其中：ET为到期日T时期权价值，WT为到期日T时参考实体资产价值。模型假定资产价值Wt服从几何布朗运动：dWt= WWtdt+σWWtdZ，其中 W为资产预期增长率，σW为资产波动率，两参数取值均为常数，dZ为标准维纳过程。

KMV模型以期权定价理论为基础，结合信用风险分析模型的思路，利用期权估值模型、期权与标的资产间敏感性关系式，建立联立方程组，倒推出估值日t时资产价值Wt。

以Black-Scholars模型计算出的t时股票市场价值Et为：

其中：

rf表示无风险利率，N（·）为标准正态分布的概率分布函数。

由伊藤定理，股票市场价值Et与资产价值间的关系可描述为：

由式（2）和式（3）可知，股票波动率σE满足条件：

利用一段时间内可观测的股票市场价值Et及其波动率σE数据，求解由方程（2）和方程（4）组成的联立方程组，估计每个交易日资产价值Wt，并据此计算资产价值增长率 W和波动率σW。

t时估计的缓释凭证到期日？子参考实体不发生破产违约的概率为P =P（W？子≥B？子│Wt）=P（lnW？子≥lnB？子│Wt），由资产价值Wt服从几何布朗运动，？子时资产价值变动过程可表示为：

据此可得公司不发生破产违约信用事件的概率为：

（三）支付违约概率

支付违约概率计算思路与破产违约概率相似。资产变现价值变动过程以 tWt表示，参数 t表示t时资产变现率，取值介于0～1之间，反映资产变现能力， t值越大表明公司资产流动性越好，变现能力越强，其值越小表明公司资产流动性越差，变现能力越弱。参数 t随时间推移而变化，称之为时变变现率。由伊藤定理可得资产变现价值 tWt服从几何布朗运动：d（ tWt）= tWt[ Wdt+σWdZ]，其中 W= W+ 。特别地，当参数 t不随时间变化时， W= W，为恒定变现率情形。与公式（5）类似，时变变现率假设前提下，t时估计的到期日？子时公司不发生支付违约信用事件的概率为：

四、模型应用

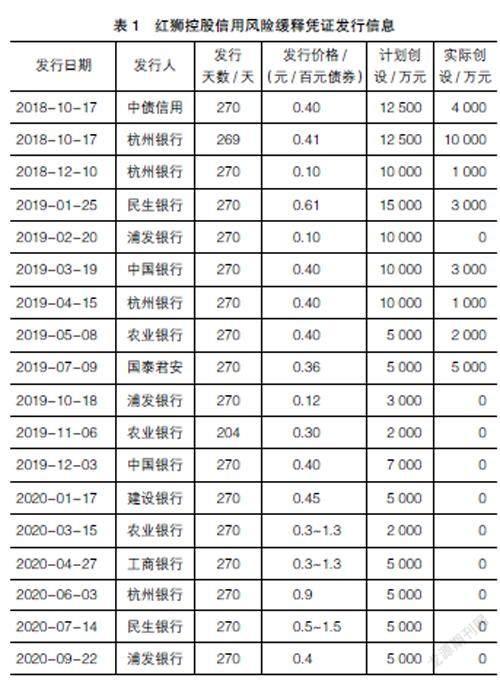
本文选择红狮控股集团有限公司（以下简称红狮控股）为对象，2018年、2019年、2020年市场发行参考红狮控股短期融资券的CRMW产品分别为3单、9单和6单，针对该参考实体债务发行的CRMW产品数量排名居前，其中发行成功8单，未成功10单，发行基本信息见表1。选择红狮控股为对象，着眼于以下两点考虑：一方面，针对公司短期融资券的缓释凭证产品发行频率高，市场影响力大;另一方面，从发行成功率和发行价格的变化中，观察公司信用风险动态变化特征对凭证价格的影响。本文选择2018年10月17日、2019年1月25日、2019年4月15日和2019年7月9日发行成功的信用风险缓释凭证为对象，应用前述CRMW理论定价模型，估计凭证理论价格，并对相关因素做敏感性分析。

（一）相关参数选择

红狮控股是一家非上市公司，营业收入主要来自水泥相关产品，因其股票价值及波动率无法直接获取，本文选择中证水泥指数②作为参照，以缓释凭证发行日前250个交易日该指数收益波动率作为红狮控股股票收益波动率σE的替代，同时计算水泥指数成分股平均市盈率，以行业平均市盈率为基础估计红狮控股股票价值，选择定存整取一年期利率作为无风险收益率。水泥行业相关股票交易数据、水泥行业相关公司财务数据、无风险利率rf数据取自CSMAR数据库，红狮控股财务数据、短期融资券发行信息、缓释凭证发行信息取自上清所网站和银行交易商协会网站。

本文以距离估值日最近一个资产负债表日“短期负债+1/2*长期负债”作为应偿还债务余额总额BT值的近似，以公司资产负债表短期负债信息披露“短期借款（商业银行融资的流动资金贷款）+应付票据（向商业银行融资的银行承兑汇票）+其他流动负债（超短期融资券和短期融资券）”计算得到公司短期有息负债B1？子。

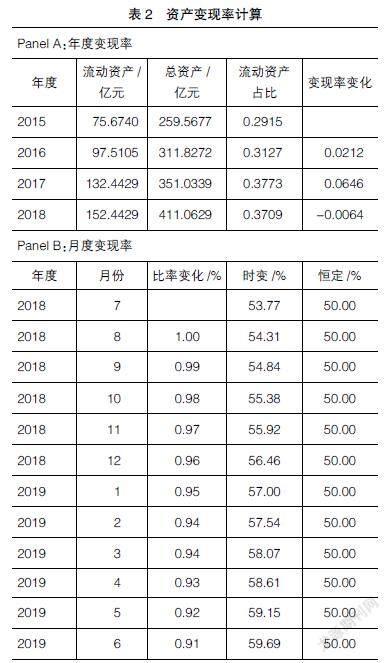
2015—2018年间，红狮控股流动资产占总资产比例平均为35%，考虑部分长期资产的变现能力，将恒定资产变现率参数值选择为0.50，时变资产变现率相关估计结果见表2。针对2014—2019年间103个主体发行的288只未结束违约流程且无偿付记录违约债券的统计表明[ 13 ]，我国债券平均估算现金回收率为23.50%，地方国有企业估算现金回收率约为30%，民营企业估算现金回收率约为10%。综合考虑红狮控股行业地位、竞争能力和财务信息，本文将现金回收率参数？茁设定为地方国有企业和民营企业债券平均现金回收率的平均值，取值为0.20③。

（二）估值过程

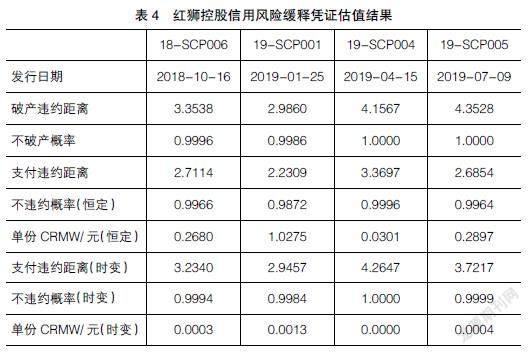
首先，基于迭代法求解方程组，估计方程（2）和方程（4）建立的联立方程组中的未知参数，得到估值日前250个交易日中每个交易日的资产价值Wt，以此为基础计算资产价值增长率的平均值 = ln（），并计算资产波动率σW，由伊藤定理可得资产价值增长率 W= + σ2W/2。其次，以上述参数估计值为输入变量，结合其他参数取值，利用公式（5）计算债券存续期内参考实体不会发生破产的概率，利用公式（6）计算债券存续期内债券不会发生违约支付的概率。最后，利用公式（1）计算缓释凭证理论价格。相关参数选择见表3，估计结果见表4。

（三）估值结果及敏感性分析

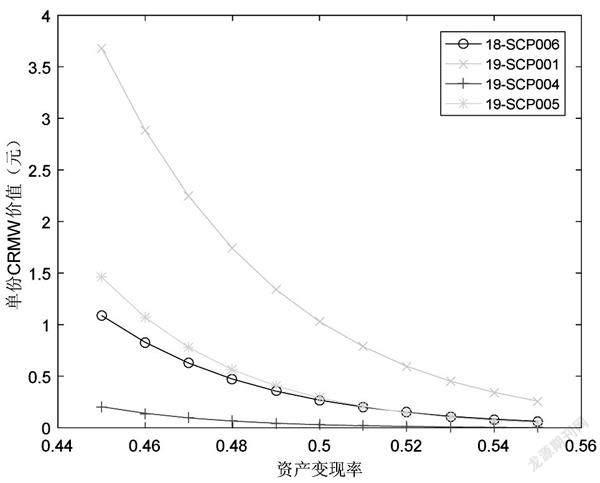
模型估计结果表明，资产变现率恒定时，参考红狮控股100元面值18-SCP006、19-SCP001、19-SCP004和19-SCP005超短期融資券所发行的单份CRMW价值分别为0.2680元、1.0275元、0.0301元、0.2897元，资产变现率变动时，同一品种的CRMW价值分别为0.0003元、0.0013元、0元、0.0004元，而同一品种CRMW产品的市场发行价格分别为0.40元（0.41元）、0.61元、0.40元和0.36元。总体而言，恒定资产变现率假设之下得到的凭证理论价格，远高于时变资产变现率假设之下相应产品的理论价格。

由于时变变现率更能准确反映资产变现能力变化情况，也更符合公司营运实际状况，基于该假设得到的凭证理论价格更为合理。各产品实际创设金额远低于计划创设金额，以及2019年10月以后参考红狮控股超短期融资券的所有CRMW产品全部发行失败的实践均表明，市场对CRMW产品认可程度较低，进一步佐证了时变变现率假设的合理性。

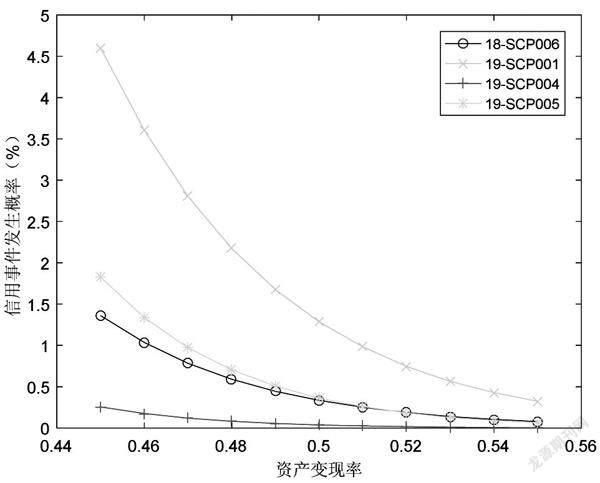
图1和图2结果显示，当资产变现率指标以0.50为基准向上或向下发生变动时，公司支付违约概率与CRMW理论价格变化剧烈，资产变现率直接影响公司发生支付违约的概率，进而与破产违约概率综合作用影响信用事件发生概率，成为影响CRMW价值的关键性要素。这一敏感性分析结果表明，模型应用过程中必须高度关注资产变现率指标选择。

五、结论

本文以计量信用风险的结构模型和简约模型为基础，充分考虑我国信用风险缓释凭证标准条款中规定的信用事件既包括参考实体出现破产，也包括标的债券发生支付违约，建立符合我国凭证产品条款实际的凭证定价模型，为我国缓释凭证定价提供坚实理论基础。

本文基于公司资产价值变动过程服从几何布朗运动假设，通过引入时变变现率参数，运用伊藤定理得到资产变现价值变动过程，进一步得到支付违约概率计量指标，并将破产违约概率与支付违约概率综合纳入缓释凭证定价过程中，构建缓释凭证理论定价模型。

本文以我国已发CRMW产品中参考实体出现频率较高的红狮控股为目标，选取挂钩红狮控股超短期融资券的四批CRMW产品为对象，采用估计KMV模型参数的基本思路，应用迭代法估计资产价值及其波动率，据此估计参考实体破产违约概率，并结合资产变现率参数，估计参考实体支付违约概率，最终得到单份CRMW的理论价格。

研究结果表明：第一，基于时变变现率假设得到的凭证理论价格较为合理;第二，支付违约风险是信用风险缓释凭证价值的重要来源;第三，资产变现率是影响CRMW产品价值的敏感性因素。本文建立的理论模型、选择的参数估计方法及采取的模型估计流程，可推广应用于我国市场信用缓释凭证产品定价过程中，助力债券投资者、债券发行人、凭证投资者、凭证发行人、资产评估机构确定合理的CRMW产品公允价值，对促进我国债券市场和信用衍生品市场健康有序发展具有积极意义。

我国资本市场尚未建立起完备的破产信息数据库和支付违约信息数据库，本文计算出违约距离后，利用正态分布概率函数计算破产违约概率和支付违约概率，未能结合参考实体所处行业、规模、资本结构等公司特质性因素建立起违约距离与真实违约概率一一对应关系，更准确地说，本文的破产违约概率应称为破产可能性指标，支付违约概率应称为支付违约可能性指标。此外，模型理论价格是市场参与主体确定产品价格的基础，最终交易价格需要市场参与者结合宏观经济、市场环境、公司财务状况尤其资产变现率等因素相应调整后得到。

本文可从以下几方面拓展研究：第一，本文以市场数据为基础计算参考实体资产价值及其波动率，据此得到CRMW的理论价格，未来可研究以资产负债表账面数据为基础计算相关参数时，破产违约概率、支付违约概率、CRMW理论价格如何变化，并分析这些计算结果与市场数据为基础计算结果间的差异及产生原因;第二，无论理论上还是实践中，资产变现率参数都是影响支付违约概率的重要影响因素，可结合我国资本市场已发生债券违约案例，利用市场数据估计变现率参数;第三，本文假定无风险利率保持恒定，可结合利率期限结构相关模型，研究随机利率情形下的缓释凭证定价模型。

【参考文献】

[1] CHOUDHRY M.Corporate bonds and structured financial products[M].Oxford：Butterworth Heinemann Elsevier，2004.

[2] CHOUDHRY M.Structured credit products：credit derivatives and synthetic securitization[M].Singapore：JohnWiley & Sons（Asia），2010.

[3] 王佳，黎晗.基于修正KMV模型的商业银行信用风险度量研究[J].经济研究导刊，2018，14（13）：47-52.

[4] 王慧，张国君.KMV模型在我国上市房地产企业信用风险度量中的应用[J].经济问题，2018，40（3）：36-40.

[5] 王传鹏，李春蕾.基于修正KMV模型的上市公司信用风险测度[J].会计之友，2018（13）：93-99.

[6] 张祥华，张梦春，丁华.基于KMV 模型的地方政府债务风险防控对策研究：以黑龙江省为例[J].会计之友，2020（2）：75-80.

[7] DOUGLAS R.Credit derivative strategies：new thinking on managing risk and return[M].Manhattan：Bloomberg Press，2007.

[8] BIELECKI T R，RUTKOWSKI M.Credit risk：modeling，valuation and hedging[M].北京：世界圖书出版公司，2013.

[9] 雎岚，施虓文.适用于中国的信用风险缓释工具定价模型[J].数量经济与技术经济研究，2013，30（1）：103-116.

[10] 张强，吴敏.信用风险缓释工具定价研究[J].证券市场导报，2012（3）：71-77.

[11] 任达，赵倩倩.中国信用风险缓释工具设计与定价实证研究[J].系统工程学报，2013，28（4）：480-487.