利用字典学习方法的声速剖面反演研究

邢传玺，张东玉，宋 扬，吴耀文，谢李祥

（1.云南民族大学电气信息工程学院，云南昆明 650500；2.哈尔滨工程大学水声技术重点实验室，黑龙江哈尔滨 150001；3.哈尔滨工程大学水声工程学院，黑龙江哈尔滨 150001）

0 引 言

目前，关于水声学研究的热点主要集中在水下定位、目标探测以及声呐系统性能的研究[1]。声速作为最为基础的水声环境参数，是了解和研究水声信道结构和水声传播的重要前提。采用直接测量的方法测量水声环境中的声速，需要耗费大量的物力人力，采用反演的方法能节省资源[1]。对于匹配场处理，海洋声速剖面的估计需要使用有限的声学数据对声场进行反演[2]。这样的反问题是一个非线性且不确定性很高的问题[3]。经验正交函数（Empirical Orthogonal Function,EOF）方法也称特征向量分析方法，被普遍应用在声速剖面的表示上，按照声速剖面样本矩阵得到经验正交函数，并取前n阶表示声速扰动，换言之，使用n个正交基表示海区的声速扰动[4]。为了在调整参数搜索大小的同时确保物理上可行的解决方案，至少需要将声速剖面（Sound Speed Profile,SSP）建模为前三阶EOF的总和来对SSP反演进行正则化[2]。但是，这种正则化方法对前几阶EOF系数具有最小能量约束，得到的 SSP估计值通常分辨率比较低。

已经有学者将K-奇异值分解（K-Singular Value Decomposition,K-SVD）字典学习应用于水声领域，用于在声传播实验中对声速剖面进行表示[5]。K-SVD算法是一种流行的字典学习方法，它通过找到向量的字典，以最佳方式对训练集中的数据进行分区，使用少数字典向量描述每个原始信号。K-SVD字典学习方法主要有两个阶段[5]：构建字典阶段以及利用构建的字典对样本进行稀疏表示阶段。这两个阶段的任何一个阶段都有许多不同算法可供选择。相对于使用主成分分析（Principal Component Analysis,PCA）得出的EOF，K-SVD算法得到的学习字典（Learning dictionary,LD）并不限于正交。因此LD能提供更好的信号压缩，由于矢量是平均的，因此更接近原始信号。

结合以上分析，本文讨论了利用K-SVD算法在声速剖面反演中的应用和稀疏表示方法，使用K-SVD算法生成了描述测量的声速剖面观测值的一维海洋SSP数据的LD，对K-SVD字典学习算法进行了说明，并根据K-SVD方法评估了重建性能。给出了LD和EOF的SSP重建结果。结果表明，与在相同数据上训练的前几阶EOF相比，所得LD中的每个字典原子都说明了更多的SSP变化，有更小的重构误差，反演精度更高。

1 基本原理

1.1 射线理论

利用水声传播实验的结果对海洋环境中的声速进行建模反演，传播模型的计算精度决定了反演结果的精度，因此选择合适的传播模型进行建模十分重要[6]。在海洋环境中，从水听器的垂直线阵列（Vertical Line Array,VLA）观察到的声压使用射线理论进行正向建模。声线模型的解是波动方程的近似解。

在直角坐标系下，射线模型中s处的声压可表示为[7]

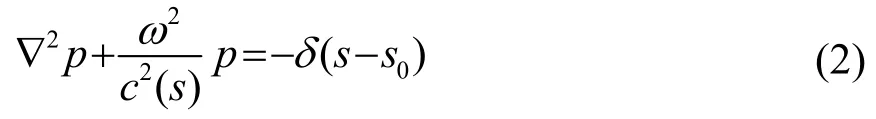
使ω的同次项相等得到声源s0到接收点s1的传播时间[7]：

1.2 K-SVD算法

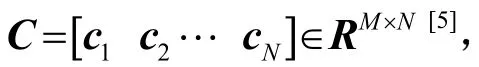
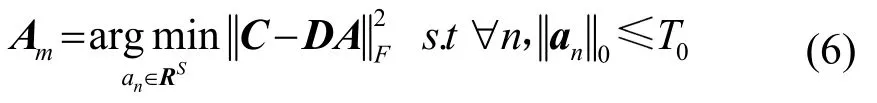
其中，T0为稀疏系数，也称其为稀疏度[10]。

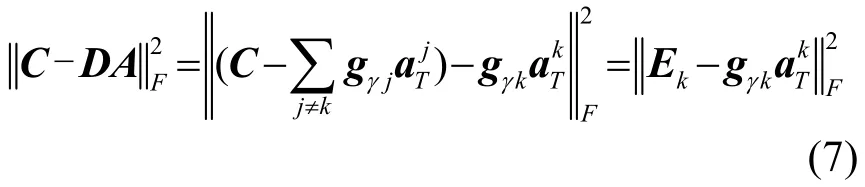
此时优化问题可描述为[10]

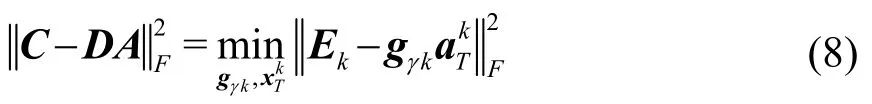
2 声速剖面稀疏表示

结合字典学习K-SVD方法，首先对实测得到的声速剖面在N个时间点进行采样，声速剖面在深度上具有M个值，得到声速剖面训练信号的集合，从获得的数据中训练SSP字典，根据式（8），利用稀疏方法中的OMP表示出训练信号的稀疏向量，对于k个元素的字典，OMP能够以k步收敛到字典元素跨度上的投影[8]。在进行有限次数的迭代之后，OMP会针对字典的所选子集提供最佳的稀疏向量值，表示声速剖面。

本文所述的反演过程实质就是利用K-SVD更新得到目标函数中最优的稀疏系数和最优字典，生成声速剖面的表示模型。

K-SVD算法反演的数据处理和声速剖面表示的流程图如图1所示。算法的输入为声速剖面训练样本C。输出为字典D和稀疏表示系数A。

计算的具体步骤如下：

（1）获取训练信号集：从实际测量的声速剖面中获得N个声速剖面，并采用插值法，插值得到深度上等距离离散的声速值，转化到K个垂直标准层，得到声速矩阵CM×N，即SSP训练样本集C。

（3）稀疏编码：使用OMP算法求解式（1）的目标方程，得到稀疏系数矩阵A。

（4）K-SVD字典更新：依次更新字典的原子，经过k次迭代后得到字典Dk。

（5）算法停止准则：停止条件设置为迭代次数或者重构信号和原信号之间的误差率，以决定迭代是否继续。

（6）算法逐列更新完字典后，用新字典Dk做稀疏分解，并判断是否达到停止条件，如果达到终止条件，得到最优字典和稀疏系数矩阵。

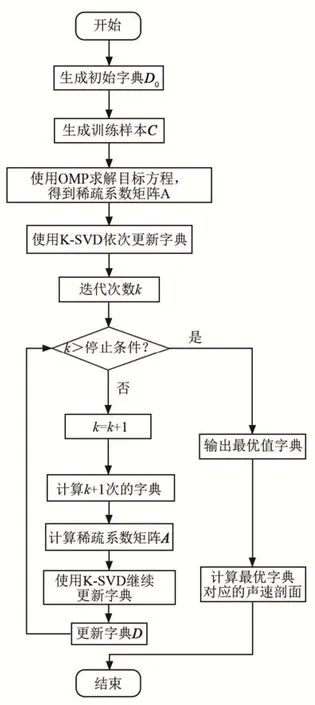
图1 K-SVD算法流程图Fig.1 The flow chart ofK-SVD

3 反演方法

声速剖面反演实质就是将测量的声场数据，通过一定的代价函数和搜索策略，估计待反演的参数，再重构形成反演后的声速剖面[11]。

仿真采用的海洋环境如下：海底为液体海底，声速为1 700 m·s-1、密度为1.5 g·cm-3、吸收为0.5 dB·λ-1（λ为波长），海水深度为25 m。发射信号频率采用200～600 Hz、长度为3 s的加Blackman窗进行幅度调制的线性调频脉冲，且声源位于水下深度10 m处，收发距离为1 km，采用1列8个均匀间隔的垂直线阵列单元，在6～20 m范围内接收声信号。

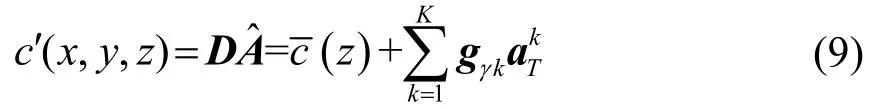
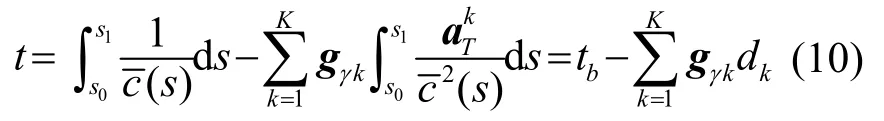
式中，tb为背景声速下的声传播时间；dk为沿背景声速下特征声线的积分小项[12]。

采用式（11）作为代价函数P：

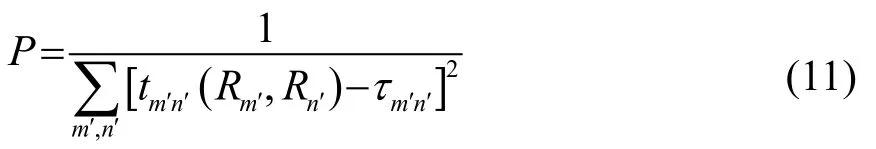
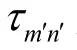
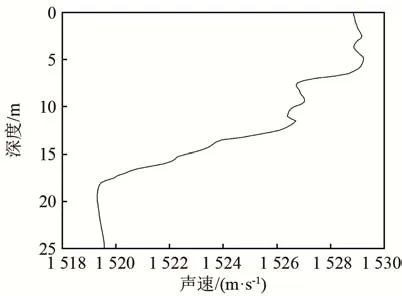
图2 进行敏感度分析的声速剖面Fig.2 A sound velocity profile for sensitivity analysis

从图3中可看出代价函数对于待反演参数的敏感性良好，且在实际值的位置出现了最大值。

声速剖面反演流程如图4所示，步骤如下：

（1）使用K-SVD算法生成的字典，来计算声速剖面；

（2）将计算的声速剖面代入射线传播模型中，进行拷贝场计算，计算得到本征声线的传播时间，并将计算结果代入代价函数与测量真值进行匹配[14]，根据代价函数的计算结果，重新生成字典，重新生成一个新的声速剖面；

图3 反演参数对应的敏感度因子Fig.3 Sensitivity factors of inversion parameters

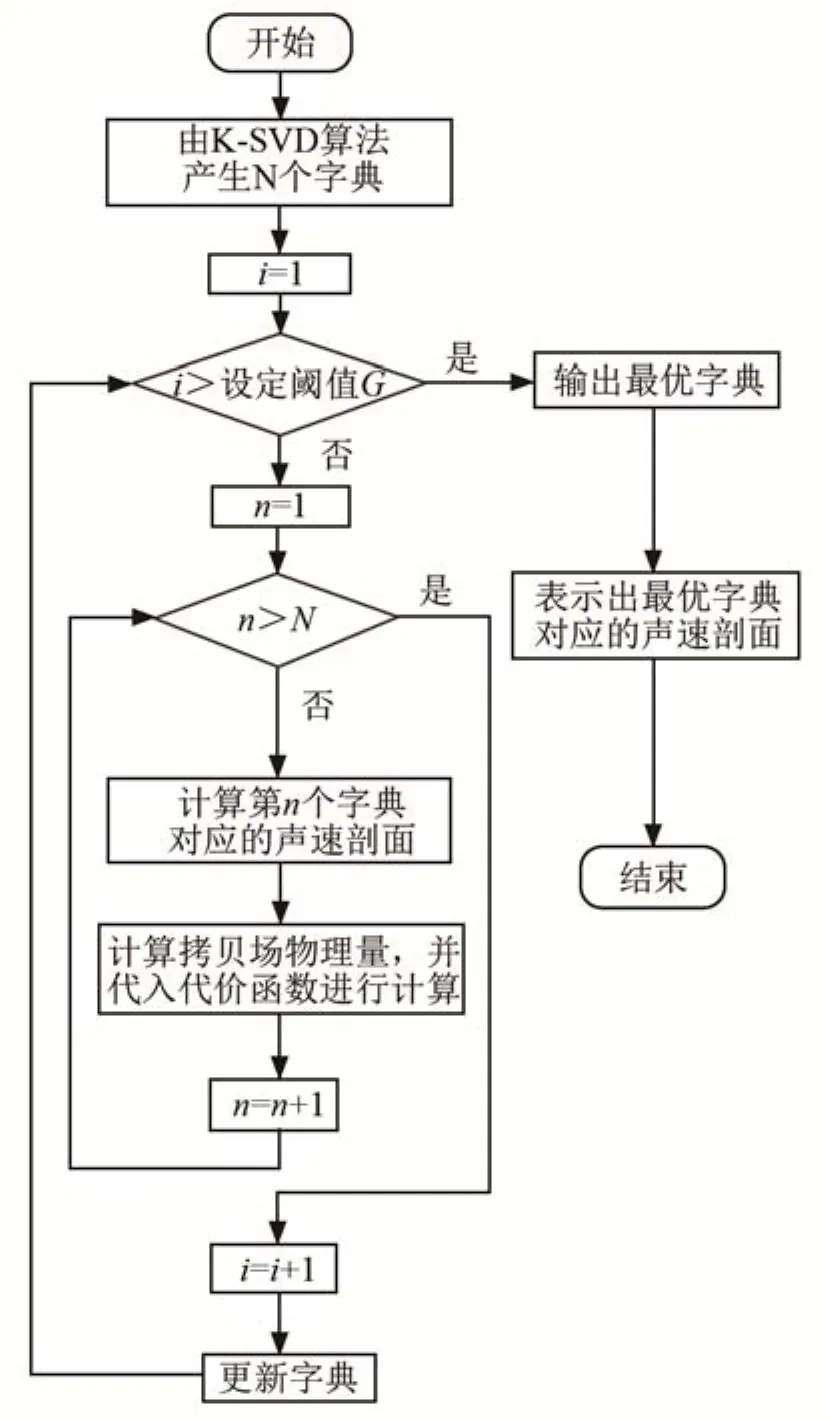
图4 声速剖面反演流程图Fig.4 The flow chart of SSP inversion

（3）重复步骤（2），在没有达到设定的阈值G前不断计算；

（4）完成初始设定的代数计算后，如果得到的结果最优值收敛在某数值附近，则说明反演算法稳健[6]，将代价函数取得最优值时的字典代入式（9）求解声速剖面，并将其作为最终的反演结果。

4 实验分析

为了验证字典学习方法优于EOF方法，利用中国黄海某海域进行的声速剖面反演实验测量的声速剖面数据进行EOF和K-SVD方法的验证。声速剖面取自作者分别于2013～2015年期间在中国黄海某海域利用温盐深系统（Conductivity,Temperature,Depth,CTD）测量的实际数据。该数据记录了0～25 m深度范围的CTD测量数据，深度分辨率为0.1 m。通过将原始CTD数据转换为SSP并减去平均值，可以从数据集中获得训练样本。将采样序列中的50（N=50）个声速剖面作为训练集。使用保形三次样条插值将配置文件统一下采样至K=25点[13-15]。SSP样本集如图5所示。

首先检验K-SVD方法对训练样本的重构性能，用50个声速剖面样本集来训练K-SVD算法的LD，图6分别显示了使用EOF和K-SVD方法生成的经验正交函数和字典原子对声速变化的方差贡献率。从图6可以看出，EOF方法生成的经验正交函数只有前5阶经验正交函数的系数可以提供有关海洋SSP变化的信息，采用K-SVD方法生成的所有字典原子都能够提供海洋声速变化的有用信息。

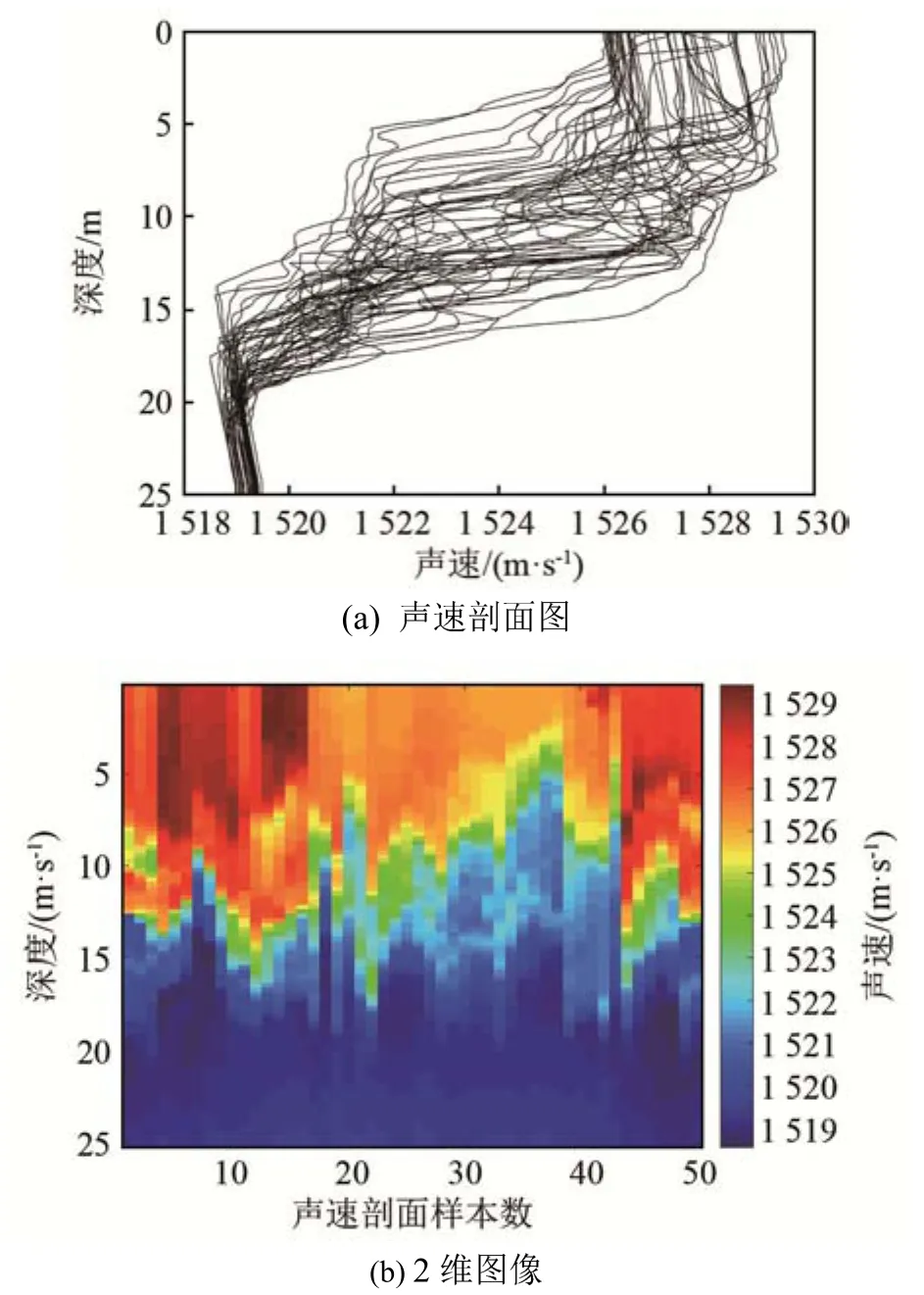
图5 声速剖面样本及其2维图像Fig.5 Sound speed profile samples and their two dimensional representation

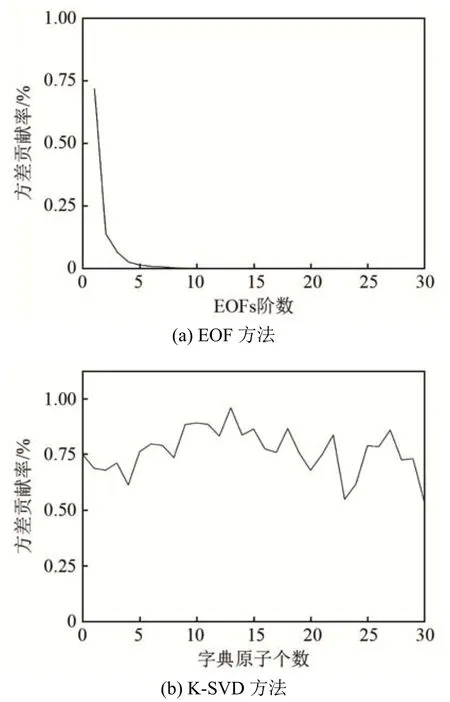
图6 EOFs阶数和字典原子数对声速变化的方差贡献率Fig.6 Variance contribution rates of EOFs order and number of dictionary atomics to variation of sound velocity

采用一个随机矩阵作为训练的初始字典，将实际测量的 50个样本作为训练字典的样本数据集，用除去样本集外的其他测量数据，来进行声速剖面的反演实验。

测量数据来源于2013年在中国黄海某海域测量的数据，实验分别采用爆炸声和线性调频信号作为声源信号，其中线性调频信号频率为 200～600 Hz，声源位于水下10 m深处，利用矢量水听器和4元垂直阵接收信号，矢量水听器位于水下9 m深处，4元垂直阵的深度范围为5～10 m，收发相距10 km。字典原子数K设为20，稀疏度T设为2，每次实验的迭代次数为120次。反演了10条声速剖面，反演结果如图7所示。

为了进一步验证字典学习方法对于声速剖面反演的优点，使用EOF方法生成的第一个经验正交函数的系数作为K-SVD算法的初始字典，对实测的声速剖面进行反演。

使用SSP数据集Y来训练EOF和LD，使用平均误差（Mean Error,ME）来度量两者的重构性能。平均误差EM可表示为[13]

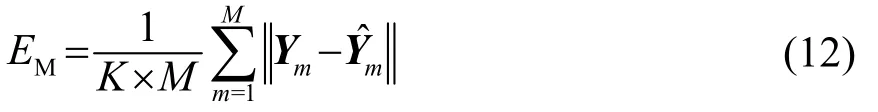
图8（a）是使用EOF方法选前3阶经验正交函数作为基函数得到的反演剖面。图8（b）是使用K-SVD方法得到的一组反演剖面。同等条件下，进行30组反演实验，EOF方法的重构平均误差为0.690 4 m·s-1，K-SVD方法重构的平均误差为0.110 2 m·s-1。从图7给出的两种方法的仿真结果以及计算的平均误差来看，K-SVD方法的重构效果优于EOF方法。结果表明，K-SVD方法仅用一个字典就可以实现EOF方法搜索选择3个以上EOF系数相同的甚至更小的平均误差。

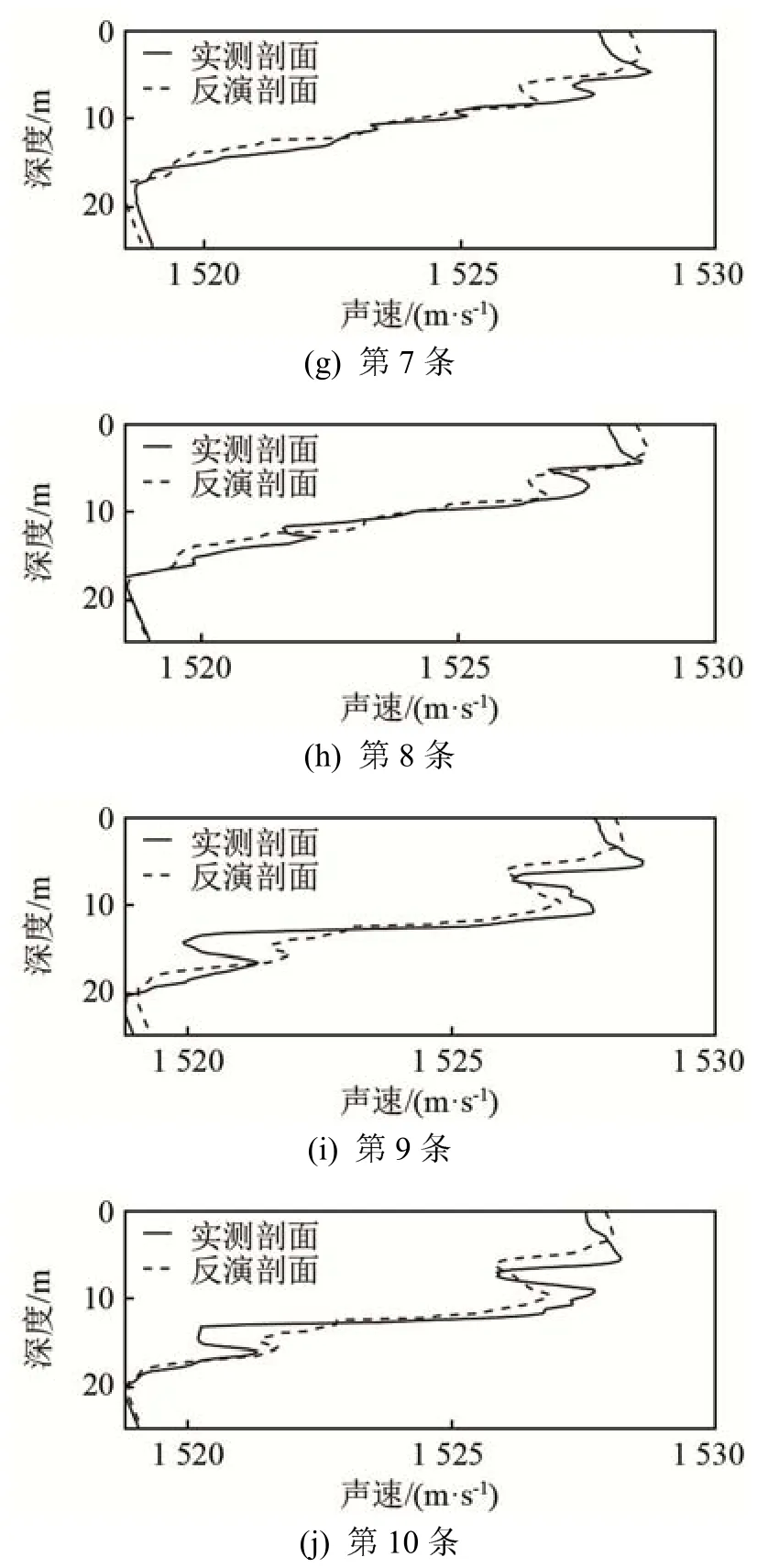
图7 10条实测声速剖面的K-SVD反演结果Fig.7 Inversion results of 10 measured sound speed profiles byK-SVD method

同时使用文献[6]中的混合优化算法对两种方法进行反演参数寻优，在不同的声速剖面下 EOF方法通常需要的迭代次数约是K-SVD方法的5倍。图9显示了K-SVD方法和EOF方法的平均误差收敛曲线，经过30次的迭代，EM降低了近70%。从图9中可以看出，对于K-SVD方法，收敛速度要快得多，并且EOF方法至少需要三个寻优参数，K-SVD方法只有两个寻优参数，计算效率更高。

图8 EOF方法和K-SVD方法声速剖面反演结果Fig.8 Inversion results of the measured SSP by EOF andK-SVD methods

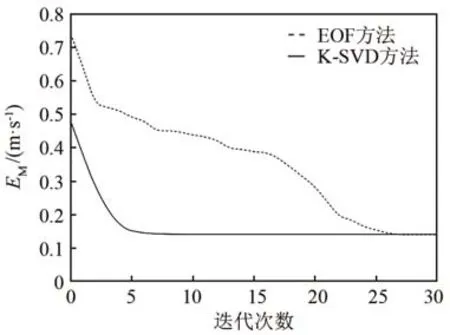
图9 两种方法的声速平均误差收敛曲线Fig.9 Convergence curves of mean error of sound velocity by the two methods

5 结 论

使用字典学习可以生成最佳字典，以稀疏地重建给定的信号。由于这些LD对正交性没有强制要求，因此生成的字典原子可以更好地拟合原始数据。相比于EOF，每个LD基函数对于信号的变化规律都是有益的。提高了基函数对于数据分布的贡献，使用很少的基函数即可近似重构信号，获得更好的反演精度。

采用K-SVD字典学习算法处理了实际测量的声速剖面数据。与EOF方法进行了对比，K-SVD算法比EOF算法使用更少的基函数即可很好地描述SSP的变化。LD中仅用一个系数即可描述每个观测到的SSP中几乎所有的变化。LD中更多的信息元素可实现这种性能提升。说明，在保证精度的前提下，K-SVD方法相比于传统EOF算法简化了算法流程，计算效率更高，平均误差降低了约50%。