基于质量-弹簧模型的驳船-桥墩冲击试验

2022-01-21李志勇王银辉李应根

湖南交通科技 2021年4期

李志勇，罗征，王银辉，李应根

(1.宁波市交通规划设计研究院有限公司, 浙江宁波 315000； 2.浙大宁波理工学院土木工程建筑学院, 浙江宁波 315000)

当代大量跨航道桥梁的建设恶化了船舶原有通航环境，船撞风险与日俱增，如何避免或减轻船舶与桥梁相撞的灾难性后果成为了各国学术界、工程界及管理部门共同关注的问题。常规用于船撞桥梁动力响应分析的非线性接触有限元方法[1]，将大量的工作投入到船舶精细化模型建立上，建模和计算效率低下，难以面向工程设计运用。

考虑到现有方法的局限性，有学者提出了基于质量-弹簧模型的简化动力分析法，简化模型以船舶为研究对象，如图1所示，将船舶简化为具有一定速度的单自由度质点，船艏与桥墩接触撞击相互作用则采用宏观的非线性弹簧单元来表征，即船舶撞击力-撞深(P-a)曲线，将简化质量-弹簧模型与桥梁碰撞，进行结构动力响应分析。经验证此类简化模型在评估远离撞击区的结构总体响应(如位移和内力)和非线性接触数值模拟相差不大。近年来源于结构抗震的冲击谱[2-3]或时程分析方法，如Consolazio等[4]提出的CVIA法(Coupled Vessel Impact Analysis),Cowan等[5]提出的AVIL法(Applied Vessel Impact Load History Method)及樊伟等[6]构建的简化相互作用模型法,逐步向船撞安全领域推广，上述方法无一例外地需要借助船舶撞击力-撞深(P-a)曲线才能开展后期的动力分析。

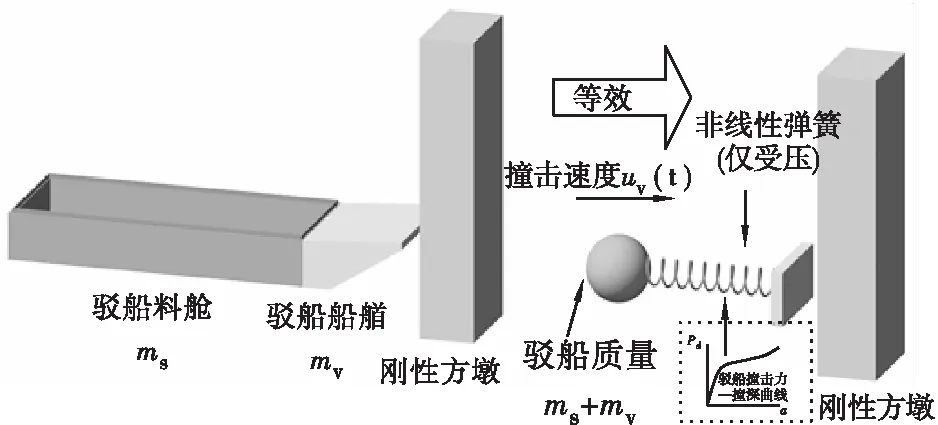
图1 基于非线性宏观单元桥梁船撞动力体系

通过以上论述可以看出，实现基于质量-弹簧模型，桥梁船撞下的动力响应求解方法需要解决的关键在于确定船-桥相互作用非线性弹簧模型及相关弹簧参数。现有文献中，AASHTO规范[7]、欧洲规范对于非线性弹簧模型以及P-a曲线也有不同函数形式的描述，王君杰等[2]通过非线性接触有限元法与基于质量-弹簧模型的方法比较，验证了其精度和实用性。Cowan[8]对驳船与不同形状桥墩(圆墩、矩形墩)的接触-碰撞问题进行数值分析，回归分析得到了驳船的P-a曲线，并发现不同形状的桥墩对该曲线影响显著，指出了AASHTO规范中该曲线未包括被撞结构形状参数的不合理性；Yuan等[9]研究指出，当船艏与桥墩的刚度比小于0.1时，大多数碰撞能量被船舶部分吸收，撞击力对桥墩刚度不敏感，但改变墩形状和尺寸对撞击力学模型参数取值影响较大。张景峰[10]、王君杰等[11-12]提出采用修正半波正弦函数作为驳船-桥墩撞击力的近似荷载模型，利用驳船吨位、撞击速度、撞击径宽比等参数确定撞击荷载曲线；然而，上述撞击荷载力学模型以及P-a曲线的讨论仅限于固定的驳船类型(500 t的JUMBO 驳船)，对于我国航道内船舶普适性尚未可知，船艏刚度的变化也未在力学模型中体现，存在许多关键问题有待完善解决。

鉴于采用船-桥碰撞的精细化数值模拟验证基于质量-弹簧模型的简化数值模拟所得结论，缺少相关试验数据支撑，降低了简化模型计算结果的可信度。同时简化模型中诸如船舶刚度、被撞墩柱的形状等关键参数对非线性弹簧模型及P-a曲线的影响需要进一步研究讨论，基于此，本文通过质量-弹簧模型撞击6根RC墩柱试验，在试验模型满足缩尺条件的前提下，探讨不同撞击速度、弹簧刚度及被撞结构截面形式对RC墩柱撞击力，撞击持续时间的影响规律，通过等效模型和驳船精细化模型对碰撞过程进行有限元模拟，验证了两者的整体相似性，并通过试验结果与现有驳船撞击力学简化模型的分析对比，验证简化模型的适用性。

1 试验概况

1.1 缩尺关系

缩尺墩柱碰撞试验的目的是验证所提出的质量-弹簧模型适用性，鉴于驳船的刚度较大，现有实验条件下，很难用弹簧完全模拟驳船的等效刚度，只能变化不同弹簧刚度，探究其对撞击力时程曲线的影响规律，船舶原型为我国内河航道中比较常见的500 DWT驳船，表1给出了本模型试验的缩尺因子，其中缩尺比例n为1/10。

表1 模型试验缩尺因子参数量纲缩尺因子参数量纲缩尺因子撞击力Fn2时间Tn尺寸Ln弹簧刚度FL-1n位移Ln撞击质量FL-1T2n3速度LT-11

1.2 构件设计

试验共设计了如图2所示的6根不同截面的RC矩形柱及圆柱。其中矩形试验墩的截面尺寸为：20 cm×20 cm、25 cm×25 cm、30 cm×30 cm；而圆形试验墩的直径为：16、20、25 cm，截面尺寸和配筋见图2,部分制作完成的RC试验墩柱见图3。其中试件纵筋等级为HRB335，直径φ 14，纵筋保护层厚度 25 mm；箍筋等级HPB235，直径φ 8，箍筋间距为70 mm，试件混凝土实测强度为44 MPa。

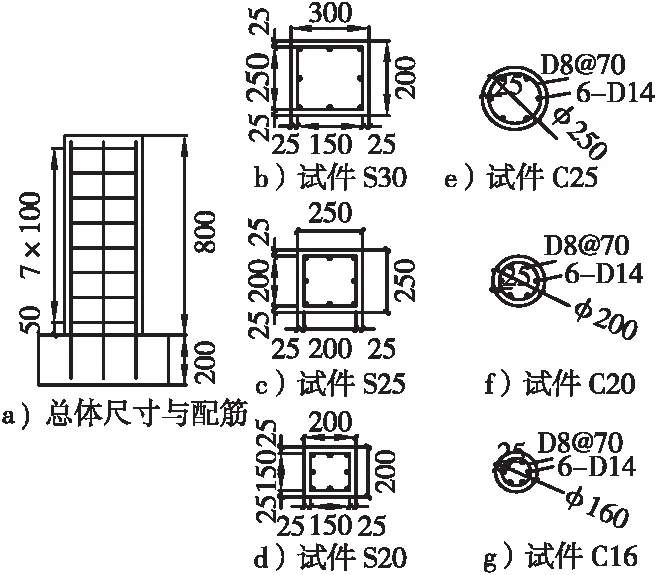
图2 RC柱尺寸及钢筋布置(单位： cm)

图3 部分制作完成RC试验墩柱

1.3 试验装置及测点布置

通过钢框架安装撞击加载装置，撞击加载装置如图4所示。首先利用缆绳及摆杆将撞击器连接于钢框架，其中摆杆用于撞击器实现固定轨迹转动，其次采用缆绳调整撞击器提升高度，使得撞击装置分别从15°、30°及45°下落以获得不同冲击速度，最后，通过测点布置的传感器获得墩柱在撞击作用下的动力需求。试验过程中，撞击箱质量ms不变，为140 kg，如图5所示。撞击箱由弹簧组、螺杆、钢板箱及撞击面钢板4部分组成，弹簧组可以实现模拟船舶撞击过程中船艏压溃屈曲，而撞击力的大小通过撞击刚面板的压力传感器获得。测量传感器布置情况为：撞击面背面墩顶、撞击位置以及距墩底15 cm处布置有加速度传感器、LVDT 动态位移传感器各1个，用于测量桥墩撞击响应；同时，墩柱沿高度布置有若干钢筋应变片，用于测量钢筋撞击过程的动态应变。

图4 撞击试验装置

a) 质量 — 弹簧撞击箱

b) 弹簧组图5 撞击箱

1.4 试验工况

为了研究质量-弹簧模型撞击RC墩柱的动态响应特征，考虑大、中、小、刚性等4种弹簧刚度及3种撞击速度的情况，对上述6根试验墩柱均进行了如表2所示的12种工况的试验。

表2 撞击试验工况工况弹簧刚度/(kN·m-1)撞击速度/(m·s-1)工况弹簧刚度/(kN·m-1)撞击速度/(m·s-1)工况12100.66工况740.66工况22101.50工况841.50工况32102.29工况942.29工况4510.66工况10+∞0.66工况5511.50工况11+∞1.50工况6512.29工况12+∞2.29注:工况10～12未安装弹簧组,改为钢板直接撞击,由于缺少了弹簧的缓冲过程,故等效为弹簧刚度+∞

2 试验结果分析

2.1 撞击力时程对比

为了验证质量-弹簧模型简化分析船桥碰撞过程的合理性和可靠性，本文首先以某500 DWT驳船撞击桥墩获取的撞击力时程曲线为例，与上述质量-弹簧的试验结果进行分析对比。图6、图7分别给出了5 000 DWT驳船船舶模型以及船舶模型数值结果与质量-弹簧试验结果的撞击力时程对比，其中船舶撞击速度为3 m/s，质量 — 弹簧模型撞击速度为0.66 m/s，弹簧撞击刚度为2 100 kN/m。从图7可以看出，船舶模型与试验模型的撞击力时程曲线发展历程基本相近。对于驳船撞击力时程曲线，根据船艏变形过程可将时程曲线概述为以下3个阶段: ① 接触阶段，船艏接触桥墩，随着船艏甲板压溃深度逐渐加大，接触面积逐渐增加，撞击力单调上升；② 屈服阶段,船艏杆件在接触过程中不断地经历接触-弹性-屈曲-塑性状态，撞击力上下振荡，并在某一时刻达到峰值；③ 卸载阶段，船舶反向运动，脱离接触，撞击力下降为零。而对于质量-弹簧撞击力时程曲线，依据弹簧的变形历程可将时程曲线同样的划分为3阶段： ① 压缩阶段,弹簧接触桥墩后，随着弹簧压缩变形加大，撞击力逐渐加大；② 振荡阶段,弹簧组部分弹簧达到最大变形，开始回弹，但同时又有部分弹簧继续变形加载，撞击力时程曲线出现了锯齿状上下振动，并在此阶段达到撞击力最大值；③ 回弹阶段，弹簧组全部达到变形最大值，开始回弹，脱离桥墩，撞击力减小为零。由上述分析可以看出，由驳船撞击桥墩取得撞击力时程曲线与质量-弹簧撞击桥墩试验的撞击力试验曲线发展历程相近。由此可知，在保证适合的质量以及弹簧刚度前提下，质量-弹簧模型能简化船舶撞击桥梁分析过程，在保证计算精度的同时,提高驳船撞击桥梁动力响应分析的计算效率。

图6 500 DWT 驳船撞击圆墩

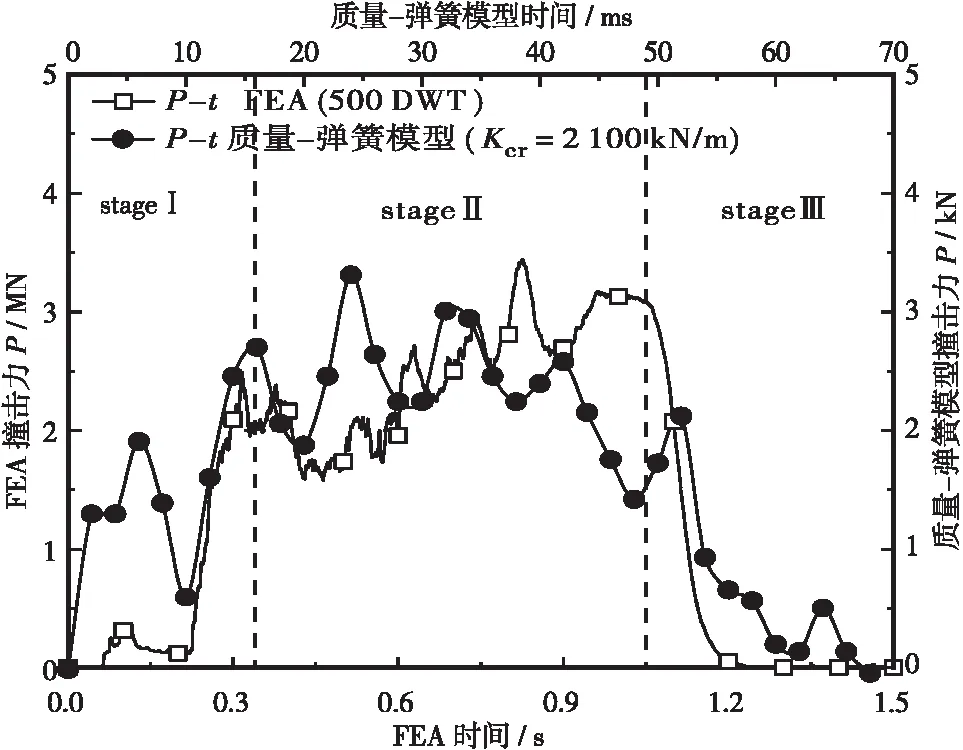
图7 撞击力时程曲线对比

2.2 撞击力时程曲线影响参数分析

船桥碰撞数值模型与质量-弹簧模型，二者变形发展阶段的相似性以及撞击力时程曲线的基本一致，初步表明了质量-弹簧模型简化分析船桥碰撞方法的可行性；在此基础上，将进一步揭示被撞桥墩尺寸、撞击速度及撞击弹簧刚度等参数对撞击力时程曲线的影响规律。图8给出了不同弹簧刚度下RC墩柱撞击力时程曲线，图中以撞击工况采用矩形墩S25、圆墩C16，撞击速度0.66 m/s为例说明，其中Td为撞击持续时间，为撞击装置接触墩柱至脱离墩柱的时间，不包含墩柱自由振动过程。不同撞击刚度下的撞击力峰值和持续时间见表3。从图8、表3可以看出，刚性撞击K0与弹性撞击力时程曲线区别较大，刚性撞击下，在接触混凝土墩柱的瞬间即产生接触力，撞击力瞬时增大，在1 ms左右达到撞击力峰值，然后迅速下降，形成简单唯一主波形，撞击持续时间在15 ms以内；而弹性撞击K1～K3下，撞击过程为强非线性过程，撞击过程弹簧压缩变形，撞击力时程曲线呈现锯齿起伏，说明在碰撞过程中弹簧体系出现了卸载回弹现象。从总体上看，撞击力随时间增加而增大，但由于碰撞曲线的波动性，使得最大撞击力的位置可能出现在碰撞过程中某个峰值处，随后撞击力起伏下降，整个撞击时间持续较长，最长持续时间达到118 ms；同时，随着撞击器弹簧刚度增加，墩柱撞击力峰值逐渐增加而撞击持续时间缩短；其中刚性撞击K0工况下，撞击力峰值最大，而撞击持续时间最短。

图8 不同撞击刚度下撞击力时程曲线

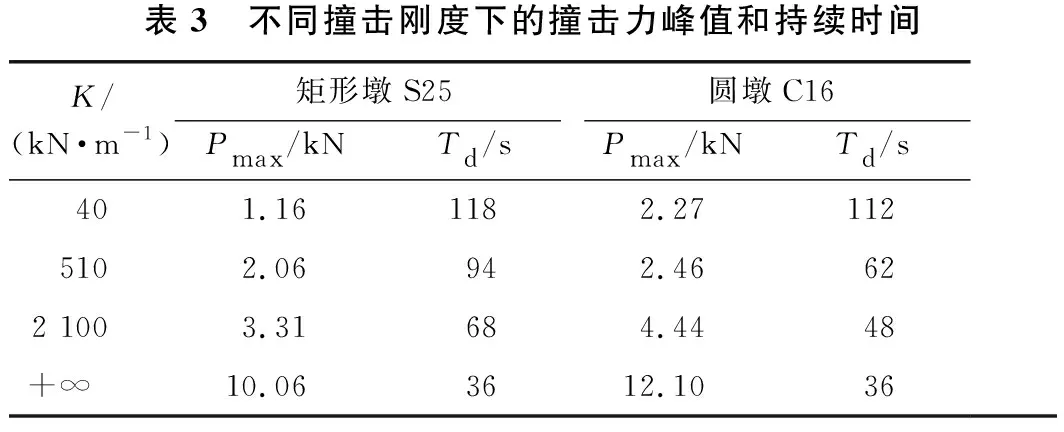
表3 不同撞击刚度下的撞击力峰值和持续时间K/(kN·m-1)矩形墩S25圆墩C16Pmax/kNTd/sPmax/kNTd/s401.161182.271125102.06942.46622 1003.31684.4448+∞ 10.063612.1036

图9给出了不同截面尺寸下墩柱撞击力随时间的变化过程，图中以撞击工况采用弹簧刚度(K)2.1×103kN/m、撞击速度(v)0.66 m/s为例说明。不同截面尺寸下的撞击峰值和持续时间见表4。由图9、表4可知：撞击矩形墩，撞击力峰值Pmax随着撞击墩柱截面尺寸的加大而加大；而撞击圆墩，截面尺寸的加大对撞击力峰值影响不大；同时，相同工况下，矩形墩撞击力峰值Pmax大于圆墩。因为矩形墩截面尺寸增加后，撞击接触面积将变大，撞击力峰值Pmax随着撞击接触面积增大而增大；而质量-弹簧装置撞击圆墩时，撞击接触面积仅为圆墩的部分表面，圆墩直径的增大却没有改变撞击接触面积，故Pmax并未变化。需要特别指出的是，尽管圆墩直径变大引起墩柱刚度增大，但RC墩柱相对撞击器刚度较大，故RC墩柱刚度变化对撞击力峰值Pmax影响不大。

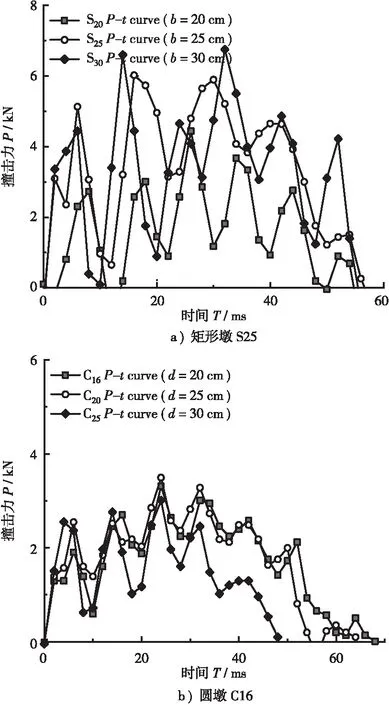
图9 不同截面尺寸下撞击力时程曲线

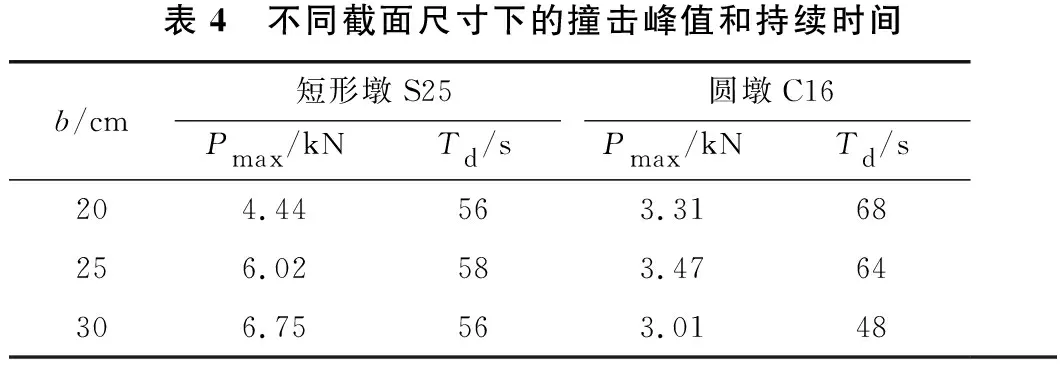
表4 不同截面尺寸下的撞击峰值和持续时间b/cm短形墩S25圆墩C16Pmax/kNTd/sPmax/kNTd/s204.44563.3168256.02583.4764306.75563.0148

2.3 规范计算值讨论

2.3.1美国AASHTO规范[7]

对于驳船，AASHTO规范建议采用双折线模型近似等效P-a曲线，用以计算等效撞击力，强度考虑屈服后强化：

(1)

式中：PB为驳船的撞击力,MN；RB=BB/10.7，为驳船船艏与被撞桥墩的宽度比，其中BB为驳船船艏宽度,m;aB为驳船最大撞深,m。

aB由下式确定：

(2)

式中：Ek为驳船初始撞击动能,MJ。

由上述可知，AASHTO规范公式驳船撞击桥墩的初始接触刚度:

Kcr=PB/aB

(3)

需要注意的是，美国AASHTO规范中考虑了驳船船艏的宽度修正，但没有考虑到被撞桥墩形状对撞击力的影响，存在不合理性。

2.3.2CVIA公式

Consolazio等[4]提出了理想化弹塑性模型近似等效P-a曲线，即CVIA公式，模型中考虑了被撞桥墩形状对撞击力的影响，计算公式如下：

(4)

式中:PBY为驳船屈服撞击力，MN；Wp为矩形(圆)墩截面宽度(直径)，m；VB为撞击速度，m/s；mB为驳船质量，t。

CVIA公式中驳船撞击桥墩的初始接触刚度:

Kcr=PBY/aBY

(5)

式中:aBY为驳船内部衔杆屈服时撞深，建议取值5.1 cm。

对比AASHTO规范与CVIA建议公式可以看出，二者撞击力屈服点Py的选择各不相同，前者采用最大撞深，后者则采用了驳船内部衔杆屈服时撞深，此外P-a曲线中被撞墩柱形状是否考虑也值得关注，上述关键问题需要采用试验数据验证其公式的适用性。

图10给出了各墩柱试件在不同工况下撞击试验得到的撞击力峰值与通过AATHSO规范及CVIA建议公式计算值的对比关系，由图10可见，AATHSO规范计算结果过于保守，而从CVIA建议公式结果接近试验数据关系曲线可以看出，AATHSO规范建议采用驳船最大撞深为撞击力的屈服转折点值得商榷，将会低估初始撞击刚度。同时可以看出，被撞矩形墩柱的截面形状对撞击力结果影响较大，而圆形墩柱影响甚微，与前述试验结果相同。综上所述，用质量-弹簧模型计算船舶撞击力时，弹簧刚度关系(P-a曲线)建议按照CVIA建议的弹塑性简化模型赋值。

图10 规范计算值与试验结果比较

3 算例分析

为了进一步核实简化模型求解驳船-桥墩撞击力的适用性，在LS-DYNA 有限元程序中建立驳船-桥墩精细化数值模型与质量-弹簧简化模型，分别对圆形及矩形桥墩进行碰撞仿真分析，通过P-a曲线对比，验证简化模型求解结果的正确性，其中质量-弹簧简化模型如图11所示。

质量-弹簧简化模型中混凝土墩柱采用实体单元(Solid164)，碰撞面板则采用壳单元(Shell163)，而弹簧组采用弹簧单元(COMBI165)模拟的撞击压溃过程。材料方面，混凝土墩柱为弹性材料(MAT_ELASTIC)，关键的等效弹簧组则采用弹塑性弹簧材料模型(MAT_SPRING-ELASTOPLASTIC)，按照CVIA建议公式，输入力-位移曲线并考虑弹簧组非线性刚度及阻尼特性，碰撞钢板采用塑性随动强化模型(MAT_Cowper-Symonds)，考虑材料应变率的塑形应变效应。

图12给出了上述弹簧以及驳船两种模型以3m/s初始速度撞击矩形墩(截面长度为1 m和3m)及圆墩(截面直径1 m和3 m)的P-a曲线。

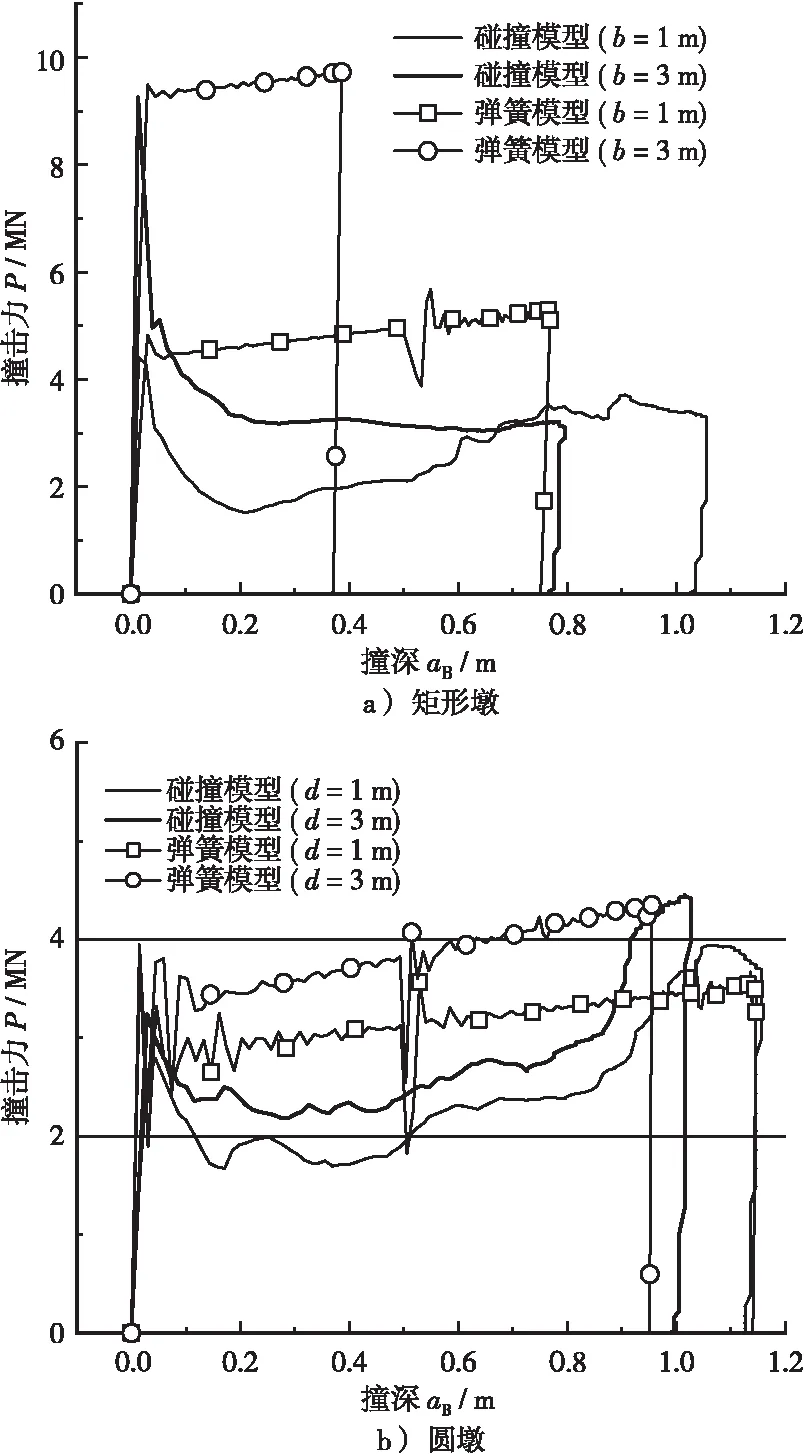
图12 撞击力-撞深比较

由图12可知，圆墩的撞击工况，采用质量-弹簧简化模型的计算结果，无论是撞击力峰值以及最终撞深与驳船碰撞模型都吻合较好；然而矩形墩的撞击工况下，尽管2类模型在撞击力峰值吻合较好，但质量-弹簧模型分析所得最大撞深明显小于驳船碰撞模型结果。原因在于驳船撞击矩形墩柱后，船艏发生剧烈变形，撞击力迅速达到峰值，结构发生塑性变形耗散初始动能，但随后船艏会发生部分回弹变形，撞击力会出现明显卸载阶段；然而，船艏采用CVIA建议的弹塑性模型表征P-a曲线，撞击力屈服后进入塑形变形并未考虑变形回弹，因此撞深计算结果偏小，但峰值撞击力结果拟合较好;同时考虑到质量-弹簧模型极大地简化了驳船模型，可实现撞击力的快速确定，满足结构初步设计阶段的需求。