基于移位内插互质阵列高分辨DOA估计*

曾耀平， 刘 洋

(西安邮电大学 通信与信息工程学院，陕西 西安 710121)

0 引 言

波达方向(direction of arrival,DOA)估计是阵列信号处理的关键技术之一，在雷达、通信、卫星导航等都发挥着重要作用[1]。近年来，由于稀疏阵列[2]更大阵列孔径和自由度，基于稀疏阵列的DOA估计逐渐受到广泛关注。文献[3]提出一种嵌套阵列，通过N个阵元最多可获得o(n2)的阵列自由度，但是互耦效应会影响波达方向估计的结果。文献[4]提出一种互质阵列，用M+N-1个阵元可获得o(mn)自由度，但虚拟域的孔洞缺失导致最大可用自由度减少。文献[5]提出一种虚拟阵列协方差矩阵稀疏重建的DOA估计算法，重构虚拟域协方差矩阵来提高阵列自由度，但算法复杂度略高。文献[6]研究了基于压缩感知的互质阵列DOA估计，降低计算复杂度，但非均匀虚拟域中信息缺失以及预定义空间网格点造成估计偏差问题有待解决。文献[7]提出一种基于互质阵列内插无网格化DOA估计算法，利用了全部接收信号信息，利用所有虚拟阵元，寻找最接近内插虚拟阵列协方差矩阵的协方差矩阵来进行DOA估计。

本文提出一种移位互质阵列虚拟内插的无网格化DOA估计研究，首先对互质阵列改进形成移位互质阵列，其次对虚拟域缺失孔洞填充形成连续虚拟线阵，最后通过原子范数最小化的优化设计和内插虚拟阵列协方差矩阵稀疏重建进行DOA估计。所提出的方法进一步提高阵列孔径和自由度，解决虚拟域信息缺失和预定义网格点产生的误差，仿真结果体现了算法的有效性。

1 移位互质阵列与信号模型

简单互质阵列模型，由一对满足互质条件的均匀线性阵列以首个阵元重叠的方式构成。设子阵列1有M个阵元，间距是Nd；子阵列2有N个阵元，间距为Md；d=λ/2，共包含M+N-1个阵元如图1。本文对简单互质阵列的两个均匀线阵进行错位偏移，令阵元数为M的阵列相对于阵列数为N的阵列向后偏移M的整数倍，称之为移位互质阵列如图2。通过差集数组扩展到虚拟域，当M+N>7时，互质阵列至少含有MN个虚拟阵元,其中2(M+N-1)+1个连续均匀虚拟阵元，移位互质阵列至少含有MN+M-1个虚拟阵元，其中2(M+N-1)+2M个连续均匀虚拟阵元。在保证阵元个数不变的情况下，移位互质阵列构成的虚拟域中增加了阵元数量，提高阵列自由度。

图1 互质阵列

图2 移位互质阵列

假设目标空间有K个目标信号入射到移位互质阵列上，入射信号方位角为θ=[θ1,θ2,…,θk]T，[·]T为转置操作，则在t时刻接收信号的模型为

(1)

对于第k个入射信号的方向向量a(θk)可以表示为

(2)

(3)

式中pk为第k个入射信号的功率，E[·]为期望，(·)H为共轭转置操作，理想协方差通常取采样协方差进行近似代替，则采样协方差可由采样快拍数据表示为

(4)

当采样快拍数在平稳遍历的情况下趋于无穷时，采样协方差矩阵趋近于理想协方差矩阵，但是当采样快拍数受限时，二者之间的差异会影响DOA估计。

2 移位互质阵列虚拟域孔洞填充

为了提升阵列自由度，现将互质阵列和移位互质阵列推广至虚拟域如图3、图4。

图3 M=3，N=5的简单互质阵列的非均匀虚拟阵列

图4 M=3，N=5的移位互质阵列的非均匀虚拟阵列

虚拟阵列等价信号可以通过向量化接收信号的协方差矩阵R得到

yv=vec(R)=Avp+σ2i

(5)

式中Av=[a*(θ1)⊗a(θ1),a*(θ2)⊗a(θ2),…,a*(θk)⊗a(θk)]∈C(M+N-1)2×K,p=[p1,p2,…,pk]T包含k个入射信号的功率，i=vec(I),⊗为克罗内克积，vec(·)是对矩阵进行向量化，(·)*为取共轭，Av对应于虚拟阵列的导引向量。其中虚拟阵元位置可以定义为

V={ui-uj|，ui,uj∈S,i,j=0,1,…,M+N-1}

(6)

差集数组中有大量重复元素，非均匀虚拟阵列通过取差集数组中的唯一值得到：Sv⊆{±(Mn-Nm)|m=0,1,…,M-1,n=0,1,…,N-1}，对应的等价虚拟信号通过选取yv中相对应位置的元素获得

(7)

一对m=3，n=5的互质整数，物理阵元个数不变的情况下，互质阵列包含21个阵元位置差，其中连续阵元位置差的范围是[-7,7]，共有15个连续阵元位置差；移位互质阵列包含23个阵元位置差，其中连续阵元位置差的范围是[-10,10]，共有21个连续阵元位置差。移位互质阵列使虚拟域中阵元个数增加，自由度提高。

以上虚拟阵列均存在若干缺失元素，如果将奈奎斯特采样定理的统计信号处理方法直接引入非均匀虚拟域中，将会引起信号模型失配[8]。现有普遍做法是仅提取其中一段均匀连续虚拟阵列进行信号处理，将非连续部分丢弃[9]，非连续部分虚拟阵元所包含的有效信息未得到充分利用，导致DOA估计性能出现一定的衰减。为了利用虚拟域的全部有效信息，本文使用矩阵填充的方法，主要针对数据缺失的情况下重建矩阵[10]，具体为在孔洞位置插入虚拟阵元，将内插虚拟阵元视为未工作状态的天线阵元，将其对应的接受信号初始化为零，内插虚拟阵列初始化为

(8)

因此,得到移位互质阵列虚拟域连续的内插虚拟阵列V如图5，内插虚拟阵列为包含2(M-1)N+2M+1个虚拟阵元的虚拟均匀线阵。其中有两种虚拟阵元，一种是原始非连续虚拟阵元，一种是内插虚拟阵元。内插虚拟阵列的等价接收信号yI包含虚拟域的全部有效信息，可用于奈奎斯特采样限制的统计信号处理，式(8)中假设内插虚拟位置初始信号为0，为了实现有效DOA估计，需要优化方法恢复内插虚拟阵元位置的信号。

图5 移位互质阵列虚拟内插V

3 重构算法

首先将理想状态下内插虚拟阵列等价接收信号表示为

yC=ACp

(9)

式中AC=[aC(θ1),aC(θ2),…,aC(θk)]∈C|V|×K为内插虚拟阵列的导引矩阵。

将内插虚拟阵列分成每份含L=(|V+1|)/2个子向量，则理想条件下内插虚拟阵列等价接收信号向量可表示为Y={yc1,y2c,…,ycL}，为了进行连续化参数表示，Y的原子集合可定义为

Ω={ac(θ)eH(θ)|θ∈[-90°,90°]}

(10)

式中e(θ)=[1,e-jπsin(θ),…,e-jπ(L-1)sin(θ)]T为L个虚拟阵列和首个参考虚拟阵列之间的相位偏移，Y的原子范数表示为

‖Y‖=inf{h>0︰Y∈hconv(Ω)}

(11)

式中 conv(Ω)为原子集合的凸包，式(11)中是多采样理想虚拟信号原子范数的定义，需要做到通过最少的个数的原子对Y进行原子分解。内插虚拟阵列协方差矩阵R(z)为Toeplitz矩阵，矩阵中的所有元素可以通过其首列构造。因此，内插虚拟阵列协方差矩阵R(z)的重构可以转化为首列向量z的重构[11]。内插协方差矩阵首列z与首个参考虚拟阵列yc1所对应的等价接收信号相同，其原子范数可表示为

(12)

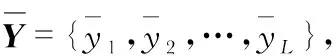
(13)

(14)

式中 〈·〉为向量中第l个元素。

通过最小化向量z原子范数的优化来重构内插虚拟阵列的协方差矩阵。需要定义一个二值向量g∈RL区分参考矩阵中的原始阵元与内插阵元，各元素值与参考虚拟阵列中的阵元一一对应，原始阵元对应的值为1，内插阵元对应的值为0。移位内插虚拟虚阵列协方差矩阵Toeplitz重构方法可表示为

subject to‖R(z)

(15)

式中G=ggT∈RL×L为构造的二值矩阵，区分Rv中的内插阵元初始化等价信号和原始非均匀阵列等价信号。为哈达马积，‖·‖F为Frobenius范数，ε为阈值参数，用于约束拟合误差。式(15)可用于凸优化问题进行求解，等价表示形式为

subject toR(z)≥0

(16)

式中ξ为权衡原子范数和拟合误差的正则化参数。同时原子范数最小化问题可以进一步表示成矩阵求迹最小化问题

subject toR(z)≥0

(17)

μ=ξ/L通过内点法可得到内插虚拟阵列重建的协方差矩阵R(z)。

对移位互质阵列内插协方差矩阵进行特征分解，由于信号子空间和噪声子空间正交，可采用谱峰搜索进行DOA估计。MUSIC算法的空间谱可以表示为

(18)

本文所提的移位互质阵列虚拟阵元内插的DOA估计算法流程。如下：

1)一对满足互质条件的均匀线阵；2)移位互质阵列；3)通过式(4)求移位互质阵列采样协方差阵列；4)通过式(7)移位互质阵列虚拟域等价接收信号；5)通过式(8)内插虚拟阵列信号初始值；6)通过式(9)～式(12)对理想虚拟信号的研究，实现DOA估计连续参数表示；7)通过式(13)、式(14)构建内插虚拟阵列协方差矩阵的参考矩阵；8)通过式(15)～式(17)的优化设计，求重建的内插虚拟阵列协方差矩阵；9)通过式(18)进行谱峰搜索，获得DOA估计值。

4 仿真实验

利用MATLAB仿真实验来检验算法性能，实验采用一对m=3,n=5的互质整数。

实验1不同信源数算法的仿真性能

假设空间中有7个均匀分布于[-60,60]的信源，信噪比为20 dB，采样快拍数为T=200，互质阵列和移位互质阵列均可以对7个信源进行有效实现如图6(a)；当信源增加到10个时，互质阵列空间谱估计存在信源缺失情况，移位互质阵列可以对这10个均匀分布于[-45,45]的信号进行有效估计如图6(b)；通过本文算法，虚拟域连续阵元范围是[-13,13]，从而可以对13个均匀分布于[-60,60]的信源有效实现如图7。说明虚拟阵列内插能够有效利用虚拟阵列所提供的全部阵列自由度。

图6 自由度性能对比

图7 虚拟内插下的自由度性能

实验2 不同信噪比和快拍数下算法精度性能估计

为了验证改进算法的估计精度，定义均方误差数学表达式如下

(19)

式中K为波达方向个数，Q为蒙特—卡罗次数，θk,q为第q次蒙特—卡罗实验的第k个信号的估计角度，θk为第k个DOA。取Q=200的实验平均值为最终结果。本文算法对比于简单互质阵列MUSIC算法和移位互质阵列SS-MUSIC算法如图8所示。根据仿真结果表明，随着信噪比的不断增大和快拍数的不断增加，本文算法均方根误差最小，因此本文算法性能优于原互质阵列算法和移位互质阵列空间平滑算法。

图8 算法精度估计性能对比

5 结 论

针对互质阵列可估计信源数不足，自由度仍低的问题。本文提出一种移位互质阵列内插虚拟阵列协方差矩阵无网格化重建算法，对互质阵列进行移位处理，明显增加虚拟阵列阵元数量，提高阵列自由度；采用虚拟阵元内插的方法，将非均匀虚拟阵列转变为一个均匀虚拟阵列，增大虚拟阵列孔径；最后，通过对原子范数最小化的优化设计和协方差矩阵稀疏重建来进行DOA估计。仿真结果表明：本文算法将虚拟域信息全部有效用于DOA估计中，极大地获得自由度的提高，并且无网格化重建算法使估计精度等性能也有较大提高。