一种基于非线性惯性权重的海鸥优化算法

秦维娜，张达敏，尹德鑫，蔡朋宸

(贵州大学 大数据与信息工程学院，贵阳 550025)

1 引 言

为解决现实生活中的复杂优化问题，来自生物和自然物理现象的启发，提出了被囊群算法[1](Tunicate Swarm Algorithm，TSA)、浮游算法[2](Mayfly Algorithm，MA)、旗鱼优化算法[3](Sailed Fish Optimizer，SFO)、绯鲵鲣优化算法[4](Yellow Saddle Goatfish Algorithm，YSGA)等优化技术以解决各领域的优化问题.

海鸥优化算法(Seagull optimization algorithm，SOA)是由Dhiman和Kumar在2019年提出一种新的基于生物行为启发的元启发式算法[5]，其思想源于自然界中海鸥的迁徙和攻击行为，与遗传算法和粒子群算法相比，SOA算法易于实现、参数调整简单，因此被用来解决一些计算量较大的问题，在实际的工业应用中也被证明了它的适用性[6].

但是，海鸥优化算法存在的易陷入局部收敛，多样性差等问题，尤其在解决一些比较复杂的多峰搜索问题中.目前，针对海鸥算法的改进是加入Lévy飞行机制[7]，通常通过增加种群的规模对算法的性能有一定的改善，但同样存在缺陷：1)不能从根本上克服早熟收敛问题；2)会增加算法的运算量.在粒子群算法非线性权重的基本思想引导下[8-10]，为了更好的平衡全局搜索能力和局部搜索能力，通过引入非线性动态惯性权重调整海鸥的位置距离，使用12个基准测试函数对标准PSO，GA，SOA和本文方法进行仿真实验，测试结果表明，本文所提算法与其他3个优化算法相比具有更好的优化性能.

2 海鸥优化算法及相关参数解析

海鸥优化算法是从海鸥的迁徙和攻击模型中得到启示的一种基于群体智能的随机搜索算法[11].在使用海鸥优化算法时，每只海鸥为D维搜索空间中的一个搜索个体，海鸥的迁徙和攻击过程即为该个体的搜索过程[12].海鸥的新位置可根据最佳代理搜索的位置和迁移位置来进行动态调整，在海鸥优化算法中，每个海鸥个体包含了以下几个元素：每只海鸥的位置，以及搜索到的全局最优位置Pgbest和海鸥的适应度值.

1)迁徙(探索全局)

在海鸥飞行过程中，从当前位置移动到下一个位置，迁徙行为模拟海鸥群体的位置移动过程.因此，在探索阶段，海鸥位置移动过程应满足3个条件：

a)避免碰撞：通过附加变量A定义一个模型，从而避免相邻海鸥间的碰撞，算法迭代利用附加控制因子变量A计算更新海鸥的位置.

(1)

(2)

fC的值设置为2，表示变量A的频率控制范围为[0，fC].

b)相邻经验：在模型A的控制下避免海鸥的位置冲突，海鸥群中的候选个体试图向最佳邻居所在的方向移动探索优值.

(3)

B=2×A^2×rd

(4)

rd表示[0，1]之间产生的随机值

c)移动向最佳位置搜索代理：最后，搜索代理可以更新其相对于最佳搜索代理的位置.

(5)

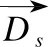
2)攻击(搜寻局部)

海鸥在迁徙过程中用翅膀和重量保持高度，并在飞行中不断的变化自身的攻击角度和速度.当需要发起攻击时，海鸥在三维平面上盘旋，x、y和z平面的运动行为描述如下：

x=r×sink

(6)

y=r×cosk

(7)

z=r×k

(8)

r=u×ek×ν

(9)

k表示随机角度值在[0，2Π]范围内，v、u是海鸥群体成螺旋状攻击猎物时的定值，r是海鸥形成的螺旋半径，e是自然对数的基数.使用式(5)-式(9)计算海鸥的攻击位置：

(10)

2.1 改进海鸥优化算法惯性权重

海鸥的迁徙行为是海鸥优化算法的一个重要部分，其中附加变量A用来控制海鸥群位置，避免海鸥在飞行的过程中发生个体间的碰撞，不产生重复的优化值，附加变量A对解决优化问题以及平衡算法有着重要作用.常用的A的更新方式如下：

A(i)= fc-i×(fc/maxgen)

(11)

其中，i为当前迭代次数；maxgen为最大迭代次数；fc为频率控制参数，初始值设置为2；式(11)表示A的值由2线性递减至0.记海鸥优化算法为SOA.

本文提出的非线性递减控制因子的海鸥优化算法(I-SOA)，该方法中A的值在递减的过程中呈现一个非线性的变化趋势(如图1所示)，可以更好的改善全局寻优能力，每次迭代既能避免海鸥之间的位置冲突，也可以更好的平衡探索与开发.该策略可以被形式化描述，如式(12)所示：

A(t)=fc-fc×(2×(t/T)exp(h)-((t/T)^2))

(12)

其中，t为算法当前执行迭代次数，T是算法执行的最大迭代次数.

图1 控制因子A随迭代次数的变化趋势Fig.1 Variation trend of control factor A with the number of iterations

在实际的算法解决优化问题中，寻优过程呈现的是一个非线性的曲线下降趋势，过程也极其复杂，因此若附加控制因子A纯粹的以线性递减的方式模拟海鸥种群的迁徙过程，就会降低实际算法寻优搜索能力.为此，本文做了2方面的改进：1)非线性变化的附加变量控制因子A与实际海鸥群体的迁徙过程更加匹配，与原SOA算法相比，非线性的前期骤减和后期缓慢递减能够加快算法的收敛能力，使算法搜索精度更加准确；2)附加变量A的值受h的影响，增加A取值的随机性，随机指数与遗传算法的变异因子类似[13]，这将有助于保持种群的多样性.

2.2 莱维飞行

莱维飞行提供了一种随机游走机制来正确控制局部搜索，这种机制被用来进一步缓解SOA过早收敛的缺点，它是由法国数学家Paul Levy提出，增加算法种群位置的多样性[14]，它描述如下：

Le(γ)≈μ-1-φ

(13)

(14)

(15)

其中，0<φ≤2，D、G～N(0，σ2)，Γ(x)是Gamma函数，μ表示步长，φ=2/3.

增加莱维飞行后更新的海鸥群体更新位置算法部分为：

(16)

算法执行流程如图2所示.

Step2.计算海鸥群体随机初始位置的适应度值，并通过比较找出最优适应度值.

Step3.根据式(12)利用改进后的非线性公式计算

新的附加变量A的值.

Step4.根据式(1)-式(16)计算新的海鸥位置，并检查更新后的位置是否越界.通过非线性的控制权重因子A对海鸥的迁徙位置更新，能够提高算法前期搜索寻优的的全局能力增强算法后期迭代寻优的局部搜索能力，其次，莱维飞行能够增加海鸥种群攻击位置的多样性，寻优精度提高的同时避免算法后期寻优局限局部最优.

图2 算法执行流程图Fig.2 Algorithm execution flow chart

Step5.得到海鸥更新的位置，再次计算更新后的海鸥个体位置适应度值，通过比较再次更新的位置和最优适应度值.

Step6.算法执行是否运行至最大迭代次数，若运行到达则算法结束；若不满足，则跳转到Step 3继续搜索.

3 仿真实验及分析

3.1 测试函数

实验采用12个典型基准测试函数以及4个不同的群智能优化算法进行对比分析(如表1所示)，其中f1、f2、f3、f4、f5是多峰函数，对算法的全局探索能力有更好的检验能力；f6、f7、f8、f9、f10、f11、f12为单峰函数，用来评估算法寻优精度以及收敛速度.

表1 本文选用的12个测试函数Table 1 Nine test functions selected in this paper

3.2 算法测试分析

将所提出的I-SOA算法与标准PSO、GA、SOA算法对比实验，从而验证所提I-SOA的算法性能.函数变量维数D=30，种群规模N=100.T=1000，A的起始值为2，实验重复执行30次.实验结果统计30次运行的最优解均值(Mean)和标准差(Std.Dev)，具体实验结果见表2.

表2 各算法的优化结果(D=30，N=100)Table 2 Optimization results of each algorithm(D=30，N=100)

从表2可以看出，本文所提出的I-SOA算法在7个测试函数上具有较明显的优势，而且在f6上的结果也只是略差于SOA算法，因此可以说明本文所提出的I-SOA算法有较高的寻优能力.此外，从12个对比函数可以看出本文提出的I-SOA算法相比标准PSO，GA的寻优结果都好，尤其对于f2、f4来说，I-SOA的收敛速度提高，因此，本文的I-SOA算法求解问题具备更好的性能.

本文的I-SOA算法通过非线性的递减附加变量A控制避免碰撞的海鸥迁徙到新的位置，能够有效的解决原SOA算法所存在的问题，并且加快算法的收敛速度，在较少的迭代次数中搜索到函数优值，增强算法稳定寻优性能.

图3-图14给出4个优化算法在12个测试函数求解优值的迭代次数和适应值变化曲线图.从图中可以看出，I-SOA在绝大部分测试函数中都具有更快的收敛速度，并且I-SOA除了在单维函数f7、f9上略差于PSO外，在其他测试函数上均能在少的迭代次数下取得函数的最优值，附加变量控制因子A的非线性递减策略能够充分的模拟海鸥群体迁徙过程的位置更新过程，更加精准的对应算法的寻优过程，使算法有更高的寻优精度，更快的收敛速度.

图3 函数f1的收敛结果对比Fig.3 Comparsion of convergence results on f1 function

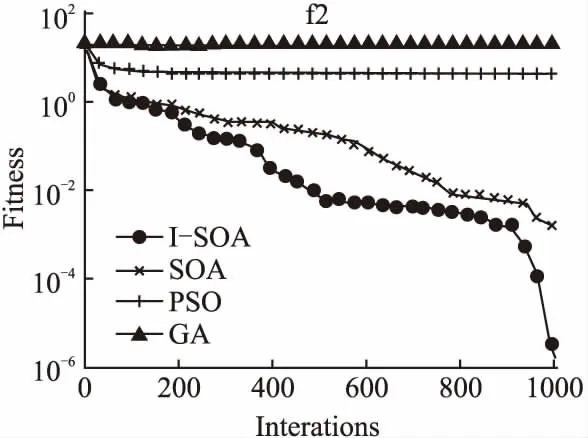
图4 函数f2的收敛结果对比Fig.4 Comparsion of convergence results on f2function

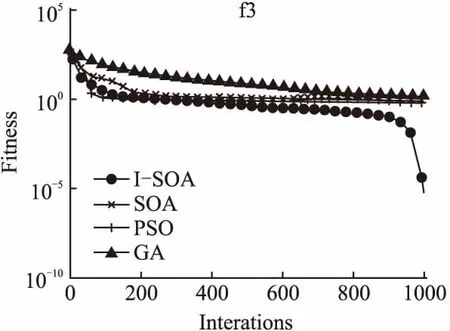
图5 函数f3的收敛结果对比Fig.5 Comparsion of convergence results on f3 function

图6 函数f4的收敛结果对比Fig.6 Comparsion of convergence results on f4 function

图7 函数f5的收敛结果对比Fig.7 Comparsion of convergence results on f5 function

图8 函数f6的收敛结果对比Fig.8 Comparsion of convergence results on f6 function

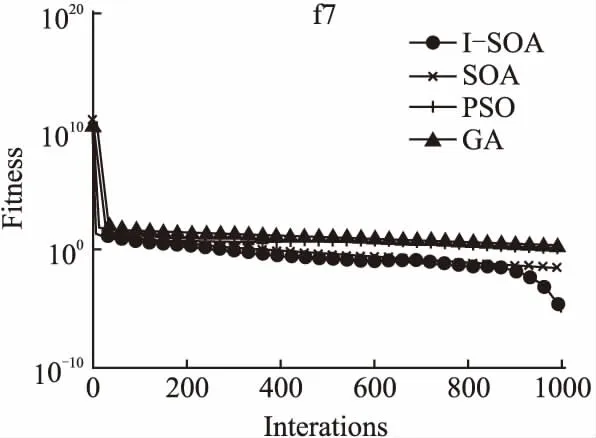
图9 函数f7的收敛结果对比Fig.9 Comparsion of convergence results on f7 function

图10 函数f8的收敛结果对比Fig.10 Comparsion of convergence results on f8 function

图11 函数f9的收敛结果对比Fig.11 Comparsion of convergence results on f9 function

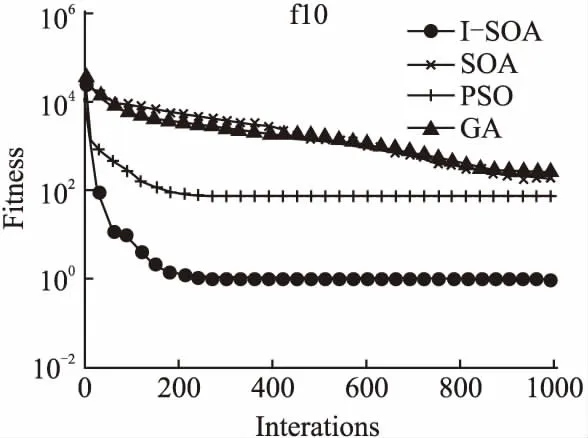
图12 函数f10的收敛结果对比Fig.12 Comparsion of convergence results on f10 function

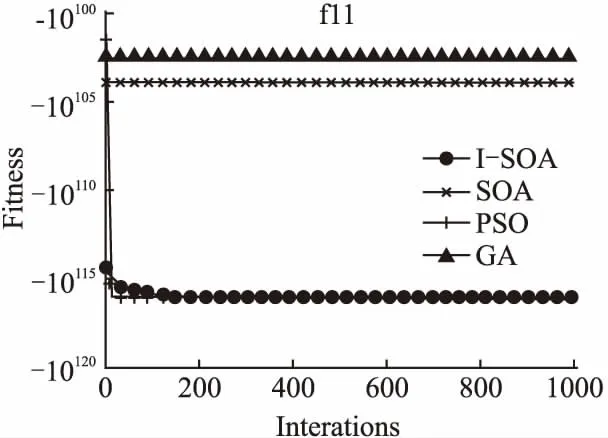
图13 函数f11的收敛结果对比Fig.13 Comparsion of convergence results on f11 function

图14 函数f12的收敛结果对比Fig.14 Comparsion of convergence results on f12 function

4 结束语

本文提出的一种非线性改变控制因子A的值的海鸥优化算法(I-SOA).一方面，突破了原有算法中附加变量A呈线性递减的约束，既能避免了海鸥位置的冲突，又能让算法获得更好的全局寻优能力和跳出局部收敛的能力.另一方面，随机因子h和莱维飞行增加种群的多样性.仿真结果表明：对比于标准PSO、GA算法和SOA算法，I-SOA算法的寻优性能有了显著的提升，加速算法的收敛和提高算法的求解精度.将I-SOA算法解决实际场景解决问题验证算法性能，将是下一步的研究内容.