基于G-DPSO算法的决策树轴承故障诊断方法

2022-01-20张炎亮颜健勇

工业工程 2021年6期

张炎亮，颜健勇

(郑州大学管理工程学院，河南郑州 450001)

对机器可用性需求的日益增长，使得制造业中对旋转机械的轴承故障诊断重视度也在加强。一直以来，人们对能够自动可靠地决定机器健康状况的技术用于机器状态监测的振动分析已被证明是近几十年来工业中的一种受欢迎的工具。轴承广泛应用于飞机、汽车、机床等现代机械设备，所以对其故障分析十分必要。通常，故障诊断包括故障信息的采集、故障特征提取和故障模式识别。故障特征提取方法有很多[1-4]，影响机械设备正常运行因素的多样性和故障信号表现行为的多变性使得准确提取信号特征较为困难，因此，如何准确提取轴承故障特征信息是当前故障诊断领域研究的重点问题。Narendiranath等[5]为了对轴承故障状态进行检测，使用经验模态分解(empirical mode decomposition，EMD)和Hilbert-Huang变换(HHT)进行特征提取。Dhamande等[6]考虑齿轮和轴承的复合多故障，从振动信号的连续小波变换和离散小波变换中提取新的复合故障特征。Hamed等[7]探讨在不进行预处理、解调、去噪和滤波的情况下，利用时域和频域的统计特性对轴承的振动信号进行提取。Lahmiri[8]将VMD与EMD进行比较，使用信噪比和均方误差作为性能指标。

在故障模式识别中，人工神经网络[9-10]、支持向量机[11-13]、决策树模型[14-15]等作为智能识别器在机械故障诊断领域得到了广泛的关注和研究，取得了良好的应用效果。然而，任何模式识别问题中，任何模式识别系统中最重要和最不可或缺的任务之一是使用特征选择方法来克服维数问题的诅咒。在过去几年中，从初始集合中选择特征的算法的选择是大量研究的焦点，并且已经提出了大量算法，其中，粒子群优化算法(particle swarm optimization，PSO)在特征选择中的应用引起了很多关注。唐晓红等[16]通过粒子群算法迭代寻优的特性寻找非局部均值算法(non-local means，NLM)的最优M和P参数，以此消除噪声并提取故障信息。李鑫等[17]采用PSO与局部阈值算法(niblack算法) 相结合的方法，构建样本特征空间，进而进行故障诊断。Huo 等[18]采用基于PSO和基于BFGS(Broyden-Fletcher-Goldfarb-Shanno)的拟牛顿最小化算法，求解模型的最优参数，从而进行故障特征提取和故障分类。李嫄源等[19]采用PSO优化算法对分类器的参数以及所选核函数参数进行寻优，并将寻优结果与其他寻优算法结果进行比较分析，对轴承故障诊断具有较好的实用性。

随着故障诊断研究的不断深入，各类优化算法对分类参数的优化效果已经趋于饱和，传统的针对分类参数的优化已经很难取得明显的分类优化效果提升。由于特征提取困难，本文提出将PSO优化算法与分类模型相结合的方法来诊断轴承故障，在传统特征提取基础上，将G-DPSO算法与决策树模型相结合，得出识别度高的特征向量，提升轴承故障信号故障诊断效果。

1 算法实现

1.1 决策树算法简介

目前，常用的决策树算法有ID3算法和C4.5算法[20]，其主要原理如下。该算法应用了信息熵的概念，随机变量X的信息熵表达式如下。

其中，n表示X的取值，pi表示取值为i的概率。

条件熵表达式如下，它度量了随机变量X在随机变量Y的条件下的不确定度。

定义

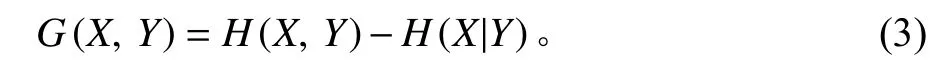
其中，G(X,Y)代表信息增益。

令子节点m上的样本集为D=(x,y)，其中x=(x1,x2,···,xN) 表示特征变量，y=(y1,y2,···,yN)表示响应变量。对于任意分裂点 θ =(a,tm)，a和tm分别对应特征变量和分裂点临界值，θ 将样本集D分为左右两枝，分别记为Dleft(θ)和Dright(θ)。

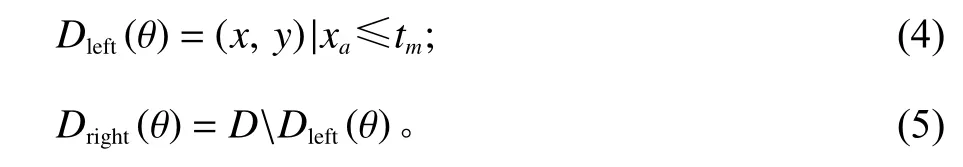
在理想情况下，子节点中的样本集是“纯净的”，但在现实中该情况较少发生。因而引入不纯度值评价不同分裂点θ。

在分类问题中，不纯度函数I表达式为

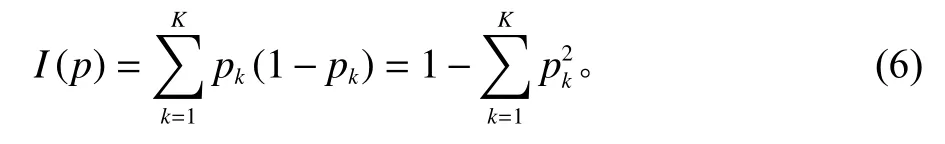
其中，K表示类别；pk表示第k个类别的概率。

令不纯度函数为I(·)，分裂点的不纯度函数I可写成

其中，|D|表示节点m上的样本数目，随后可以求得最小化不纯度函数的最优分裂点

按相同方法迭代分裂Dleft(θ∗)和Dright(θ∗)，直至决策树深度达到上限或子节点样本数少于事先规定的样本数。

1.2 基于G-DPSO算法的决策树故障诊断模型

在Kennedy等[21]提出的PSO算法中，粒子群根据评价规则，不断调整自己的位置向最优位置移动，粒子群根据自身的记忆性进行一步步的迭代，记忆迭代更新方式如下。

其中，j和d分别代表第j个粒子和第d维；T为迭代次数；M为个体最优粒子，M为全局最优粒子；粒子更新速度为vjd;c1和c2为加速因子；r1和r2为[0, 1]区间的随机数；ω为惯性权重；U(0,1)表示0∼1服从均匀分布的随机数。

目前运用广泛的PSO算法虽然拥有较强的搜索能力，是各个领域优化的研究热点，但在面对一些复杂问题时往往容易陷入局部最优解。本文对粒子的搜索速度进行限制，对ω进行动态调整，随着迭代次数进行，粒子在搜索到的最优解附近区域变慢速度，慢慢搜索，直到寻得全局最优目标。通过引入动态调整的惯性权重ωp来对粒子的速度进行动态更新，得到动态粒子群优化(DPSO)算法。

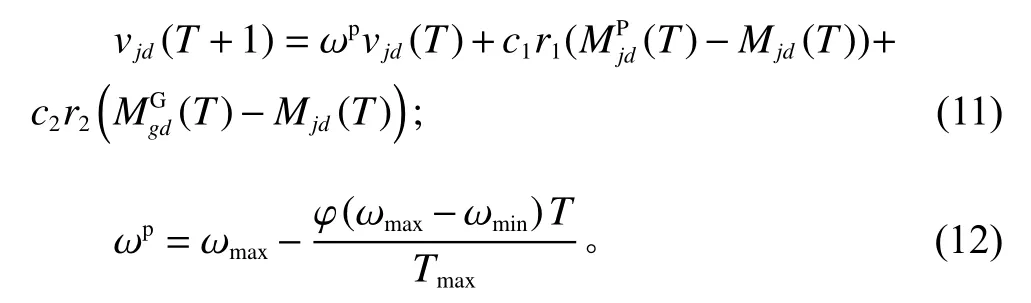
其中， ωmax和 ωmin分别表示最大惯性权重和最小惯性权重；φ为[0, 1]中随机产生的经验值；Tmax为设置的最大迭代次数。从公式中可以看出，刚开始ωp的值比较大，在 ωmax附近，随着迭代的进行，ωp的值减小，减小到 ωmin附近。由于粒子群算法中惯性权重的减小并不一定是线性的，为了保证惯性权重变小的随机性，本文通过区间[0, 1]中随机产生的经验值φ 来调整惯性权重的随机性。

在充分利用PSO算法优点的基础上，对PSO中的惯性权重进行动态调整，得到DPSO算法，再将信息熵与DPSO相结合，将信息熵增益作为DPSO的适应度函数，得到G-DPSO算法。信息熵本身就能够用来进行特征选择，这将使特征子集得到更好的验证，粒子个体质量得到更好的评价。通过DPSO算法与信息熵增益相结合的形式，根据熵增益最大的原则使特征信息分类最大化，从而找出最适合分类的几个特征变量用于分类器分类。信息熵增可以用来进行特征选择，且模型构建速度较快，作为适应度函数来评价基因子集将进一步提升故障信号特征的分类精度和选择的效率。采用决策树进行分类，运用到信息熵的知识，通过G-DPSO算法对轴承振动信号故障信号特征分类得到最佳子集，再运用决策树分类器对最佳子集进行分类，有利于进一步提高分类的准确性，提高故障诊断效果。

通过G-DPSO算法对轴承振动故障信号特征进行选择，得到类可分性最大化的最优特征子集。最后采用决策树分类模型对最优特征子集进行分类，从而实现对轴承故障进行诊断。图1流程很好地解决了故障信号特征信息冗杂和特征信息不足造成的误诊率偏高的问题，对比传统故障诊断流程以期得到更好的故障诊断效果。

图1 故障诊断流程图Figure1 Flow chart of fault diagnosis

如图1所示，对原始故障信号数据进行特征提取，在G-DPSO粒子的初始阶段，粒子的初始速度和初始位置通过以下公式产生。

通过G-DPSO算法选择最合适的特征集，使类别可分离性最大化，从而提高分类性能。

从公式中可以看出，粒子初始化后的位置里只含有数据0和1，假设总共有L个特征，考虑到每个粒子维数都要一致，本文的1代表选取该特征，0表示丢弃该特征。通过对相应位置的特征数据集进行适应度分析，根据迭代公式进行迭代，不断得到新的最优个体粒子和全局最优粒子，直到迭代结束。输出此时得到的全局最优粒子，其对应的特征集数据则是类可分性最大化的特征集数据。

将得到的特征集数据分成两份，一份用于训练决策树模型，另一份用来测试决策树模型精度，从而实现对轴承故障进行诊断。

2 实验分析

2.1 数据收集

本文使用的振动数据来自西储大学轴承数据中心网站的轴承测试数据集[22]。西储大学轴承数据中心网站的轴承测试数据集数据和故障种类众多，为减少数据的分析量，同时保证数据的有效性，从数据库中选取5种故障类型。5种故障分别为外圈故障断层直径为0.007 in (0.017 18 cm)、滚珠故障断层直径为0.007 in、内圈故障断层直径为0.007 in、内圈故障断层直径为0.014 in (0.035 56 cm)、内圈故障断层直径为0.021 in (0.053 34 cm)。根据轴承故障位置不同，在故障断层尺寸为0.007 in时，选取外圈、滚珠和内圈3种故障类型；根据轴承故障断层直径不同，在轴承内圈分别选取故障直径为0.007 in、0.014 in和0.021 in，3种故障。

2.2 信号处理和特征提取

为了便于计算机数据处理，本文将外圈故障设为1，滚珠故障设为2，内圈故障3种不同磨损尺寸0.007 in、0.014 in和0.021 in分别设为3、4和5，每种故障状态收集40组样本，每组样本为3 000个样本点，5种状态共200组样本，共600 000个样本点。将每种故障状态的40组样本的前25组作为训练样本，5种状态共125组；后15组作为测试样本，5种状态共75组。

特征提取在基于振动的故障诊断中非常重要。采用不同的特征提取方法对最终的模型精度测试结果有很大的影响。特征提取方法有很多，本文主要从振动信号的幅域、频域提取特征。

在幅域中，通过对信号进行处理可以提取不同统计特征：平均值、均值标准误、标准差、中位数、极差、偏度、峰度、方差、均方递差等9个特征。文中统计特征结果具体由Minitab软件计算获取。

在频谱域中，原始信号的频谱通常不包含有关轴承故障的诊断信息，因为故障脉冲会被结构共振放大。小波变换是很好的频谱处理方法，使用db10小波进行尺度为5的分解，以其中一个样本为例，对故障信号进行分解和重构，其中一个样本的原始信号和重构信号图如图2所示；对故障信号进行分解后得到1 ～ 5层高频细节信号如图3所示，从而运行得到第1层高频细节信号的包络谱(如图4所示)。从包络图中可以得到每组样本数据的能量熵，每组样本数据的能量熵是轴承故障数据中的一个比较重要的特征。同时，采用小波包变换方法，输入信号时域图像，对每组故障信号进行4层小波分解(如图5)，求得小波包分解后各个频段的样本能量(如图6)。

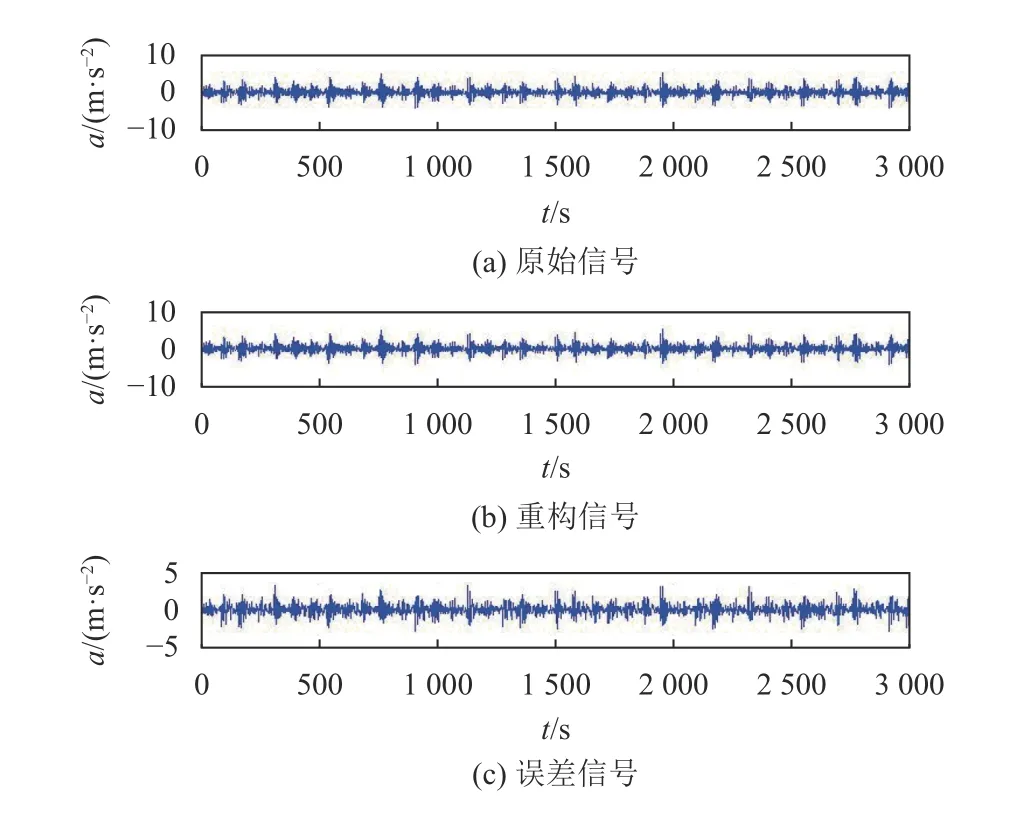
图2 故障信号重构Figure2 Fault signal reconstruction

图3 小波分解后的1 ～ 5层高频细节信号Figure3 1-5 Layer high frequency detail signal after wavelet decomposition

图4 高频信息包络图Figure4 High frequency information envelope map

图5 4层小波分解图Figure5 Wavelet decomposition diagram

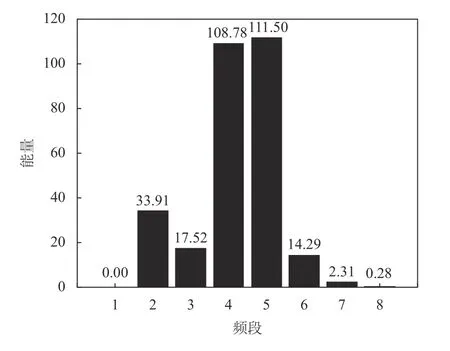
图6 各个频段能量图Figure6 Energy diagram of each frequency band

分别对所选的200组轴承故障信息样本数据进行运算，提取出200组具有18个特征变量的轴承故障信号特征向量数据集。通过结合信息熵的G-DPSO算法对提取的18个特征进行特征选择，得出最优子集，转换后得到相应的8个特征向量集；同时，采用主成分分析方法(principal components analysis，PCA)对提取出的18个特征向量集进行降维处理，得到PCA集，采用决策树模型对特征数据集进行故障诊断分析。

3 轴承故障诊断方法性能评估

为了验证模型方法的有效性，采用决策树分类模型分别对不同的特征变量所对应的轴承故障信号特征向量数据集(单特征集、全体特征集)进行分类预测测试，以及对G-DPSO算法优化后的特征变量相对应的轴承故障信号特征向量数据集(最优特征集)进行分类预测测试，同时与采用PCA方法提取的故障数据特征集进行分类预测对比。其分类预测结果如表1所示，表1为采用4种不同集合对不同故障类型的综合预测结果，图7 ～ 10分别为PCA集、全体特征集、单特征集和最优特征集对故障类型的诊断结果。

图7 故障诊断结果(PCA集)Figure7 Result of fault diagnosis (PCA sets)

表1 故障诊断测试结果Table1 Fault diagnosis test results %

图8 故障诊断结果(全体特征集)Figure8 Result of fault diagnosis (entire features sets)

图9 故障诊断结果(单特征集)Figure9 Result of fault diagnosis (standard error sets)

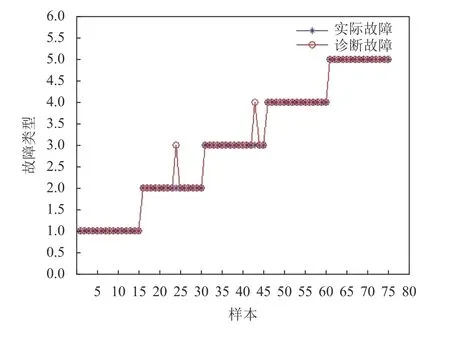
图10 故障诊断结果(最优特征集)Figure10 Result of fault diagnosis (the selected sets)

从结果分析来看，对最优特征集进行故障诊断时得到的诊断分类准确率比较高，高于97.3%，验证了模型方法的有效性。当只考虑故障位置1、2、3这3种故障类型时，无论是采用单特征还是全体特征，故障诊断准确率都偏低，低于90%。当只考虑轴承故障断层尺寸大小时，由于实验中选取的故障尺寸(0.007 in、0.014 in、0.021 in)成倍数关系，尺寸相差较大，易于区分故障类型，选取合适的单特征和选取全部特征进行故障诊断，诊断效果很好，准确率都高达100%。当对5种故障类型进行故障诊断时，既有内外圈的故障区别，也有故障断层直径大小的区别，诊断准确率都有所降低。而采用全体特征或单特征数据，诊断准确率都明显下降。可见，故障类型多少对故障诊断准确度有影响。故障类型分得越细，种类越多，诊断难度越高，此时采用最优特征集得到的诊断效果最好。

从整体上分析，在轴承故障诊断中，对于简单故障，提取合适的单一特征进行故障诊断效果较好。而在实际生产过程中，轴承故障受各种因素影响，故障类型复杂，提取单一特征诊断效果有限，需要采用多特征融合提高诊断准确率。由于特征信息的冗余，故障特征向量不是越多越好，需要提取适当的特征向量集。使用G-DPSO算法优化后的最优特征集进行分类诊断结果稳定，且准确率很高，超过97%，能够到达预期效果，这也验证了优化PSO算法与决策树相结合的方法在故障诊断应用中的有效性。