带可选时间窗的车辆调度多目标优化方法

文/黄埔生 曾强

1.引言

车辆调度问题（Vehicle Routing Problem,VRP）最早由学者Dantzig和Ram ser于1959年提出，其一般定义如下[1]：对一系列装货点和卸货点，组织适当的行车路线，使车辆有序地通过它们，在满足一定的约束条件下，达到一定的目标。车辆调度的优化目标有很多，大致可分为两类：一类是有利于物流企业的目标，如配送路程最短[2]、配送成本最低[3]、配送车辆最少[4]；另一类是有利于客户的目标，如延迟时间最短[5]、满意度最高[6]等。其中，配送成本和客户满意度是两个最根本、最重要的优化目标。送货的准时性是决定客户满意度的核心因素之一。在此背景下，带时间窗约束的车辆调度问题（Vehicle Routing Problem w ith Time W indow s,VRPTW）成为一个重要研究课题。多目标车辆调度问题属于NP-hard问题。常用的多目标优化方法有“间接法”和“直接法”两种。间接法是将多目标转换为单目标、再采用单目标优化法进行求解的方法，该方法的缺点是受人工干扰因素较大且不能得到一个完整的Pareto解集以供决策[13]。NSGA算法于1994年被Srim ivas和Deb提出[7]，其优点包括非劣最优解均匀分布、优化目标数可以任意选择[8]。文献[9-10]通过对以上方法定量研究得出“NSGA算法性能优于其他算法”的结论。2002年，Deb[11]在NSGA的基础上又提出了带精英策略的非支配排序遗传算法（NSGA II），大大提高了NSGA算法的性能。基于以上分析，本文针对一类带可选时间窗的车辆调度问题，提出了一种基于NSGA II算法的多目标优化方法。

2.问题描述

某配送中心0服务于n个客户，为其配送某种货物。假设条件：①车辆完成配送后需回到配送中心；②客户的需求时间窗为软时间窗；③客户的需求时间窗不唯一；④一个客户能且只能被一辆车服务；⑤客户的需求量已知，客户的需求时间窗已知，配送中心与各客户、各客户之间的行驶路程已知，每个客户被服务的时间、车辆从配送中心出发的时间已知；⑥车辆可24小时随时出入配送中心；⑦同一车型耗油量不考虑载重量的影响；⑧车辆有w个车型，各车型数量不限。要求：合理安排车辆及其配送路径，使其配送总成本最低、平均客户满意度最高。该问题的优化目标如下：

式（1）表示配送总成本最小化；式（2）表示平均客户满意度最大化。

其中，客户满意度的度量方法如下：在软时间窗环境下，客户i的满意度可用图1所示的曲线进行度量（以客户i提供2个可选时间窗为例）。图中有 4个变量，分别为 ei、ai、bi、li，满足 ei≤ai≤bi≤li。其中，ai、bi为客户 i满意的最早送达时间和最晚送达时间，[ai，bi]为客户 i的满意服务区间；ei、li分别为客户 i可接受的最早送达时间和最晚送达时间，[ei，li]为客户i的可接受送达区间。设t是客户i的货物送达时间，则该送达时间对于客户i的第j个时间窗的满意度函数Sij(t)如式（3）所示。客户i的满意度如式（4）所示。

图1 客户i满意度度量

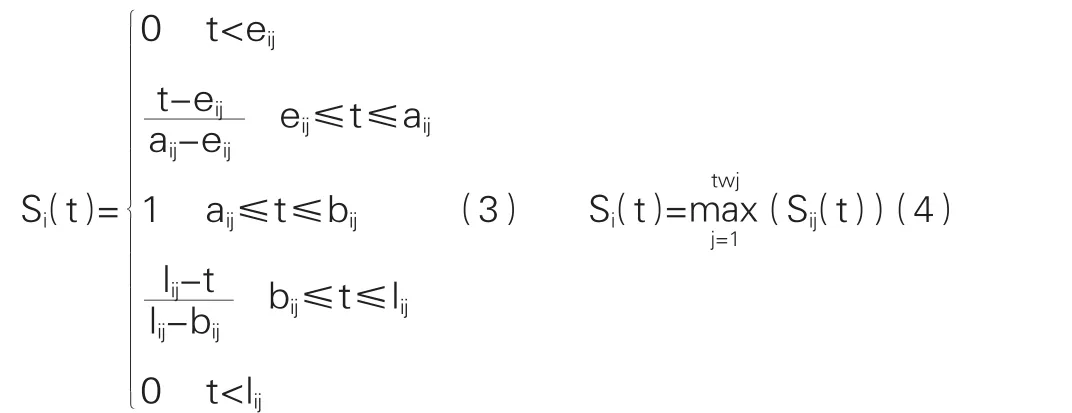
3.NSGAII算法设计

3.1 算法流程

取ps为偶数，本文算法流程如图2所示。

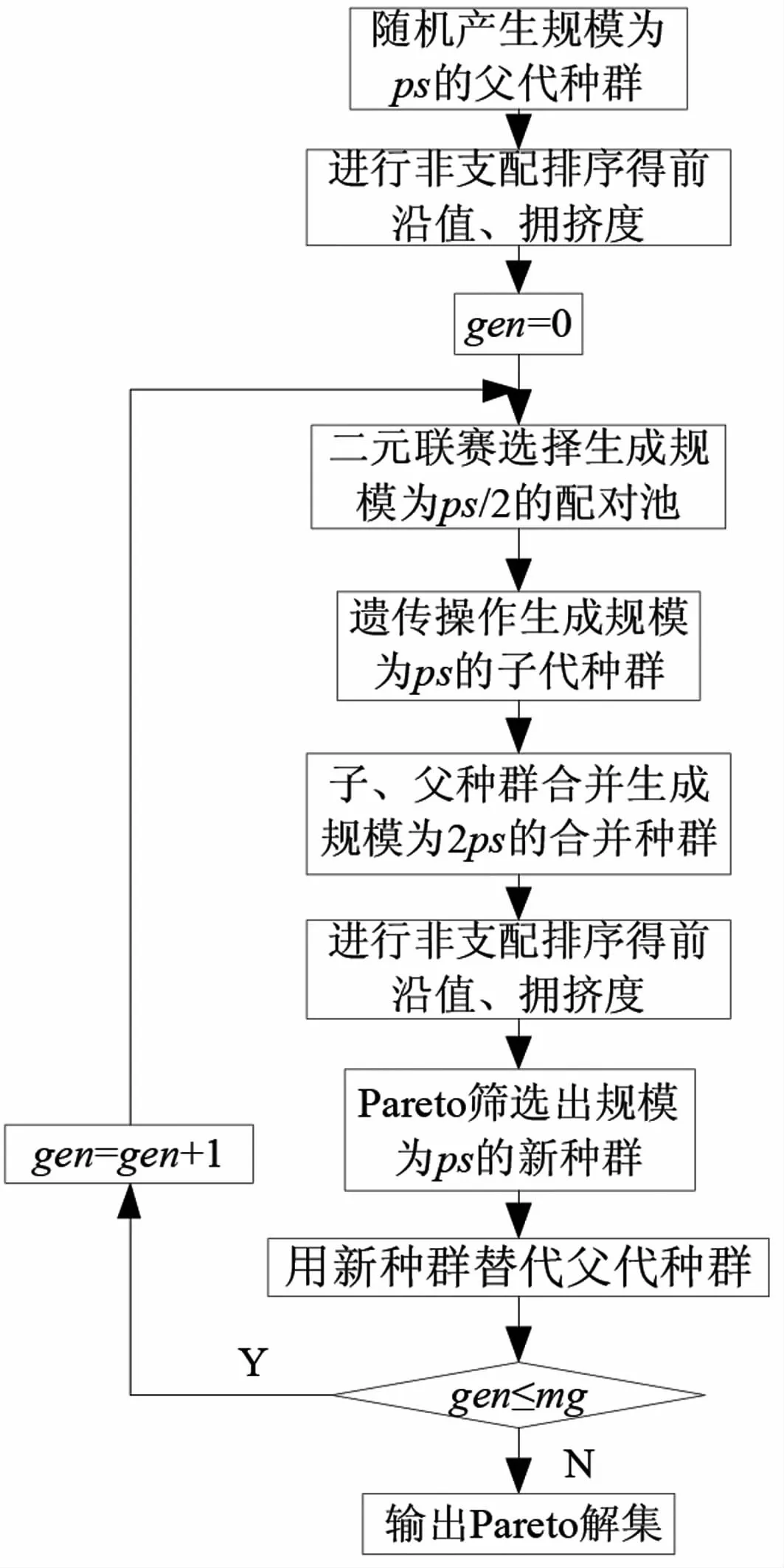
图2 算法流程

3.3 编码方式。采用“整数”方式编码[12]，用1～2dt-1的随机序列表示一个个体。图3是一个dt=13，长度为25的个体的编码。该编码表示共用6辆车进行配送。车辆1为客户7、8配送，行驶路径为0→7→8→0；车辆2为客户4、3配送，行驶路径为0→4→3→0；车辆 3、4、5、6同理。

图3 编码方式

3.5 交叉操作。采用“分段交叉”的方式进行交叉操作[21]。以dt=13为例，交叉操作如图4所示。随机产生两个长度为2dt-1的染色体A和B，其中||部分为交叉片段，同理，染色体B操作也是如此。产生的子代个体需要用到函数kexing判断其是否可行。若A’可行，则取A’，否则取A；若B’可行，则取B’，否则取B。

图4 交叉操作

3.6 变异操作。采用“两点对换变异”的方式进行变异操作[21]。随机产生两个不相同的变异点 m point1和 m point2，设m point1=6、m point2=17，变异前后的染色体片段如图5所示。同样，变异后的个体仍需要用到函数kexing进行判断其是否可行。若A’可行，则取A’，否则取A。

图5 变异操作

3.7 目标值转化。由于NSGAII算法在计算时，要求优化目标均为最大化或者最小化，故需对式（2）中所构建的目标函数进行处理。本文将优化目标中的式（2）按照式（5）进行最小化转换。

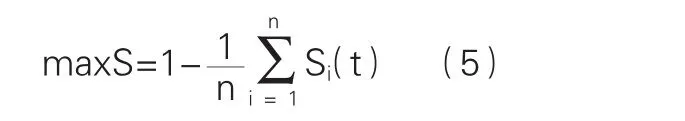
3.8 解码操作。解码操作的目的是通过个体编码解析出配送路径，然后求得优化目标：配送总成本和1-平均客户满意度。以图3所示的个体为例进行说明：配送总成本计算方法如下：由客户7、8所需货物总量，选择车辆1的车型（不低于其载重量的最小额定载重所对应的车型），以此类推，求得此配送路线的所用车型和总车数；根据各车型调车成本和车数求得调车成本，汇总得到总调车成本；将每一车辆行驶路程、单位路程耗油量、单位耗油成本相乘得到运输成本，将运输成本汇总得到总运输成本；将总调车成本与总运输成本相加得到配送总成本。1-平均客户满意度的计算方法如下：通过个体编码，求得车辆到达每个客户的时间t，根据式（3）计算送达时间t在该客户每个需求时间窗下的满意度，按式（4）计算该客户的满意度，按式（2）计算平均客户满意度，按式（5）计算1-平均客户满意度。

4.案例分析

河南省某物流企业有一个配送中心0，服务于13个客户。客户1-13为分布在13个不同城市的客户，配送中心及客户所在的城市如表1所示。现有某种货物需要为这13个客户配送，配送中心与各客户以及各客户之间的路程矩阵如表2所示。

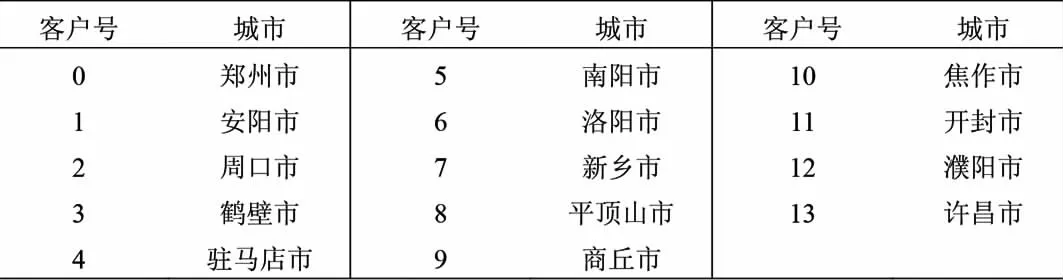
表1 配送中心及客户

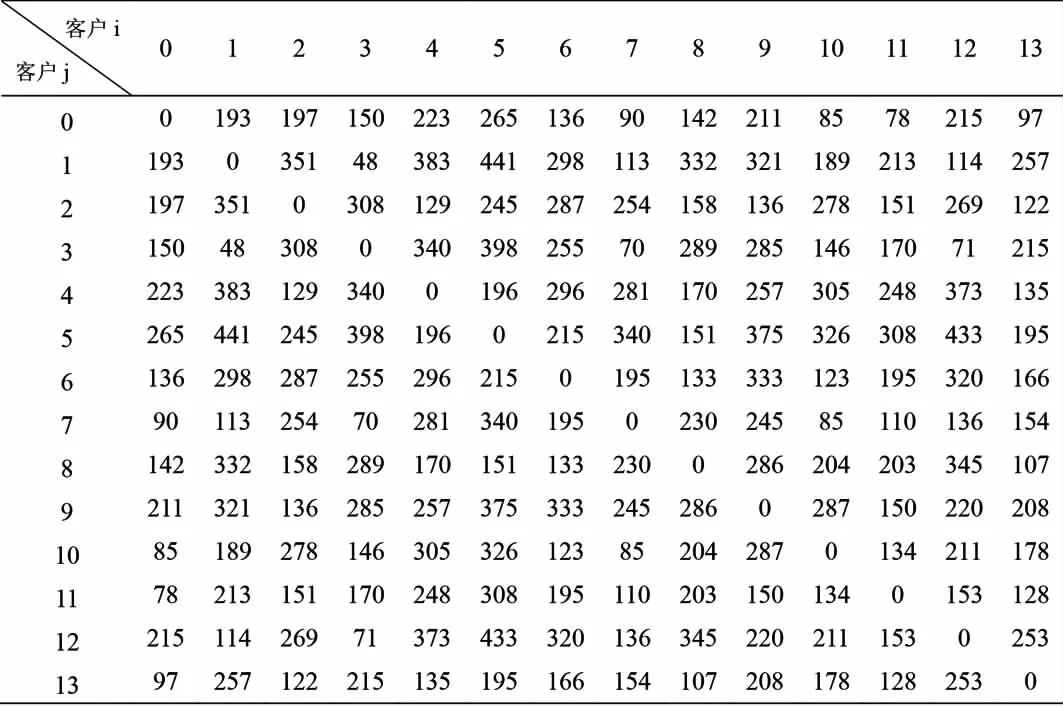
表2 路程矩阵（单位：km）

设置算法的种群规模ps为50，迭代次数m g为300，交叉比例cr为0.7，变异比例m r为0.3。设此物流企业有1、2、3、4四种车型：对应的额定载重量分别为 12t、15t、18t、21t，调车成本分别为400元、500元、600元、700元，单位路程耗油量分别为1.5L/km、2 L/km、2.5 L/km、3 L/km；各客户的货物需求量如表3所示；各客户提供的时间窗已知。配送车辆出发时间为2020/12/15 4:30，每个客户的服务时间为30分钟。

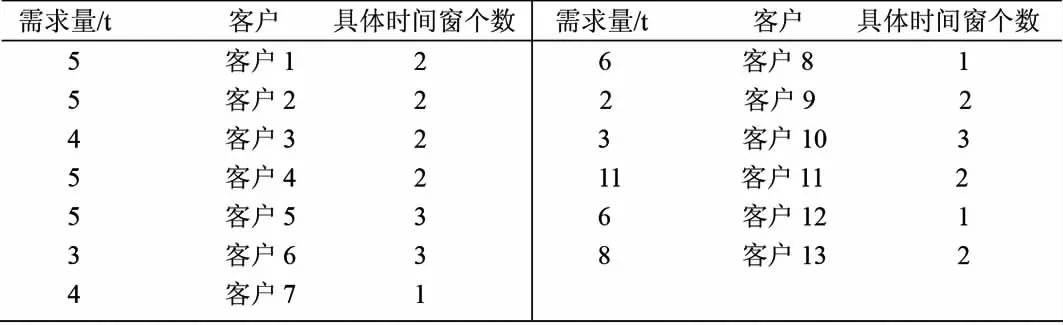
表3 客户需求量

运行算法多次，均能得到稳定的Pareto解集。图6是其中一次的输出结果。其中，Pareto解A的参数如图7所示。

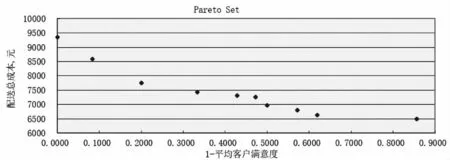
图6 Pareto解集

图7 Pareto A

图7 中,A解配送总成本为6524.3元，1-平均满意度为0.7854，是配送总成本最低的一个配送方案。共选择6辆车，分别为 5辆1型车、1辆2型车。其中车 1载重量为 15t(5+5+5=15)、配送客户分别为2、4、5，选择的是客户2的第2个时间窗、客户4的第2个时间窗、客户5的第1个时间窗；车2载重量为 12t（4+6+2=12）、配送客户分别为 7、12、9，选择的是客户7的第1个时间窗、客户12的第1个时间窗、客户9的第2个时间窗；车3载重量为12t(3+3+6=12)、配送客户分别为10、6、8，选择的是客户10的第1个时间窗、客户6的第2个时间窗、客户8的第1个时间窗；车4载重量为9t(5+4=9)、配送客户分别为1、3，选择的是客户1的第2个时间窗、客户3的第1个时间窗；车5载重量为8t、配送客户为13，选择的是客户13的第1个时间窗；车6载重量为11t、配送客户为11，选择的是客户11的第1个时间窗。为了比较可选时间窗与单时间窗的不同，把客户1-13的第一时间窗保留，其余的时间窗删除。重新计算得到单时间窗下的Pareto解集如图8所示。

比较图6和图8的Pareto解集，可以发现：当配送总成本都为6780元时，带可选时间窗的“1-平均客户满意度”为0.5733，对应平均客户满意度为0.4267；单时间窗的“1-平均客户满意度”为0.7618，对应平均客户满意度为0.2382；当配送总成本都为7000元时，带可选时间窗的“1-平均客户满意度”为0.5000，对应平均客户满意度为0.5000；单时间窗的“1-平均客户满意度”为0.7141，对应平均客户满意度为0.2859；当配送总成本都为7443元时，带可选时间窗的“1-平均客户满意度”为0.3330，对应平均客户满意度为0.6670；单时间窗的“1-平均客户满意度”为0.5000，对应平均客户满意度为0.5000；当配送总成本都为8600元时，带可选时间窗的“1-平均客户满意度”为0.0876，对应平均客户满意度为0.9124；单时间窗的“1-平均客户满意度”为0.2500，对应平均客户满意度为0.7500；即当配送总成本相同或相近时，带可选时间窗问题的平均客户满意度比单时间窗问题的平均客户满意度高。产生这种现象的原因是可选时间窗下可选择性高，使得平均客户满意度高。

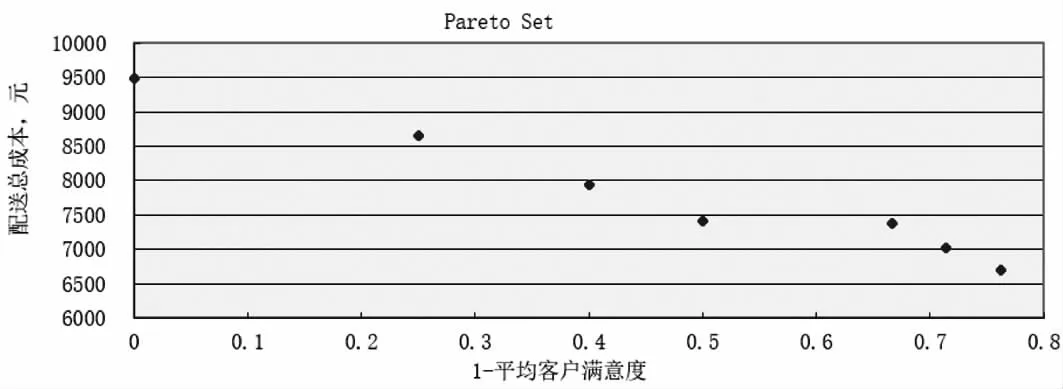
图8 单时间窗下的Pareto解集

5.结语：

针对一类带可选时间窗的车辆调度问题,提出了一种基于NSGA II算法的多目标优化方法。描述了以配送总成本最低、平均客户满意度最高为优化目标的多目标问题，设计了带精英策略的非支配排序遗传算法（NSGA II）对该问题求解。案例分析表明，当配送总成本相同或相近时，带可选时间窗问题的平均客户满意度比单时间窗问题的平均客户满意度高。本文算法收敛性较好，能够在较短的时间内得到Pareto解集，供调度员决策。