机场道面预防性养护评价指标综合改进灰色预测模型

黄学林，王观虎，龙小勇，陈正磊，李柯，陈奇奇

(空军工程大学 航空工程学院，陕西 西安 710038）

机场道面预防性养护评价指标[1]是反映道面使用性能变化规律和判定道面预防性养护最佳时机的重要指标。建立准确的指标预测模型，了解道面预防性养护评价指标的衰减变化规律，对于机场道面适时采取预防性养护措施、进行精确化管理至关重要。常用的指标预测模型按照建模原理的不同主要分为三大类：确定型模型[2]、概率型模型[3]和其他预测模型[4-5]。确定型模型以经验回归为主，易于建模，但是无法反映预测指标影响因素的不确定性；概率型模型可以描述影响因素的变异性，但是预测结果不够直观，并且需要大量的原始数据作为支撑；其他预测模型的数学方法原理比较复杂，但是能够较好地描述数据的一般规律，解决原始数据不足的问题，其中应用较为广泛的就是灰色预测模型[6]。考虑到影响机场水泥混凝土道面预防性养护评价指标衰减的因素众多，主要分为物理力学因素、外部环境因素以及内部材质因素。这些影响因素具有很大的随机性和变异性：飞机荷载的大小和横向分布是随机的；作用于机场道面的温湿度、降雨等环境因素具有很大的不确定性；受到施工材料和施工技术的影响，机场道面结构层变异性明显。鉴于众多不确定性因素的影响，不便采用确定型模型直接对原始数据进行回归分析，并考虑到军用机场数据采集困难，现有的原始数据难以建立概率型模型，本文研究构建机场道面预防性养护评价指标的灰色预测模型来解决军用机场道面“小样本”、“贫信息”的问题。邓聚龙[7]提出了灰色系统理论，此后，国内外众多学者对灰色系统理论开展了广泛的研究，在完善灰色理论的同时将该理论应用到各个领域。贾建中等[8]率先将灰色理论引入到机场道面领域，预测了反映道面使用性能的各项参数；张耀华[9]通过分析机场道面性能的历史数据，探究其内在发展规律，建立了道面使用性能的灰色预测模型；王观虎等[10]利用灰色预测理论对道面剩余寿命进行预测，建立了机场水泥混凝土道面的剩余寿命预测模型，并尝试采用结构参数优化的方式对模型进行改进。上述研究均起到了较好的应用效果，具有一定的精度，这表明灰色预测理论能够有效应用于道面性能预测研究。然而，以上研究成果仅仅是对灰色预测理论应用于道面性能预测方面的简单尝试，缺乏系统深入的研究。而且这些研究所建立的预测模型往往是针对特定对象，不能应用于道面预防性养护评价指标的预测。因此，有必要开展基于灰色预测模型的水泥混凝土道面预防性养护评价指标预测研究。

1 概况

1.1 水泥混凝土道面预防性养护评价指标体系

军用机场道面评价指标的研究主要借鉴普通水泥混凝土道面和路面性能评价指标，军用机场水泥混凝土道面与普通水泥混凝土道面和路面的路用性能评价指标的差异并不显著，军用机场道面主要依据其特殊性，主要对外观质量、平整度、防滑性能和承载强度等4个方面评价道面性能，军用机场道面与普通道面和路面性能指标的限值存在差异，同时指标下面的子指标也存在差异。本团队通过研究军用机场水泥混凝土道面的性能，构建了机场水泥混凝土道面预防性养护评价指标体系，包括结构承载强度指标、抗滑性能指标、损坏状况指标和平整度指标[11]。一般来说，道面等级号和摩擦因数随着时间的推移逐渐减小，道面破损指数和国际平整度指数与之相反，一旦超过允许的临界值，必须采取预防性养护措施。

1.2 灰色预测模型适用性分析

灰色系统理论将数据序列视为符合一定变化规律的灰色量，采取适当数据变换处理的方法，生成规律性更强的新数列，进而利用微分拟合法得到相应的生成函数。大多数数据序列经过变换处理后呈现指数规律，因此，采用灰色预测模型要求系统必须满足一定的指数规律[12]。

研究表明机场水泥混凝土道面使用性能衰减进程符合指数变化规律，根据道面病害类型和使用性能不同可以分为3个阶段：病害初发期、病害爆发期和病害稳定期。因此，道面破损指数增长趋势呈S形曲线，为满足道面正常使用要求，最好在病害爆发期之前采取预防性养护措施，一旦进入病害稳定期，一般需要采取大中修或改建措施。从图1中可以看出，处于预防性养护临界值之前，道面预防性养护评价指标发展状况符合指数规律。因此，道面预防养护评价指标的预测适合采用灰色预测模型。

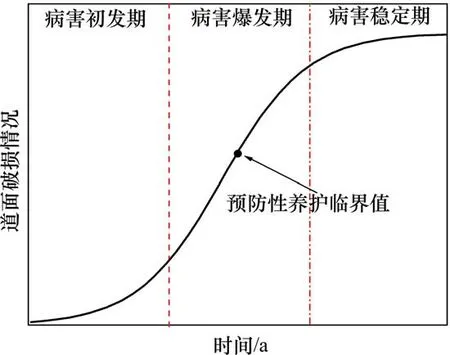
图1 道面使用性能阶段Fig.1 Usage performance stage

1.3 数据的采集与处理

由于军用机场道面性能检测数据较少，且数据的时间序列不完整，无法得到连续的预防性养护评价指标数据，为解决该问题，国内外学者进行了相关的研究，孙立军[13]提出了时间—空间转换法，把同一类型的机场道面在不同寿命时间点的道面性能状况(空间分布)当作同一道面在不同寿命时间点的表现(时间变化)，以延长数据的时间序列。本文前期研究发现，在大量历史数据的统计下，时间—空间转换法的预测精度和采用同一设施长时间积累数据所建立模型的精度是一致的，在本文研究中误差影响可以忽略。本文应用此方法，得到了某军用机场连续的预防性养护评价指标数据。

2 综合改进灰色预测模型构建

2.1 经典GM(1,1)模型

灰色预测模型是一种基于灰色系统理论的现代预测模型，该模型的优势在于利用有限的数据信息即可建立模型对未来值进行预测。GM(1,1)模型是灰色预测模型中最经典的模型，经过国内外学者的研究改进，已经被广泛应用到经济、材料、能源、交通等领域[14-15]。

定义某灰色过程的数据为原始数据序列，设序列X(0)=(x(0)(1),x(0)(2),···,x(0)(n))为原始数据序列，其中，x(0)(n)≥0,k=1,2,···,n。

设X(1)=(x(1)(1),x(1)(2),···,x(1)(n))序 列 为X(0)的1次累加生成序列1-AGO，其中：

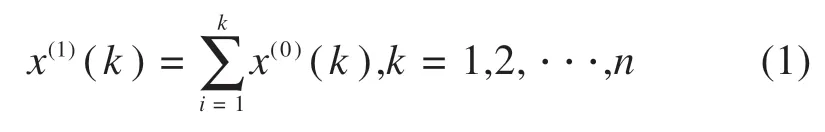
设Z(1)=(z(1)(2),z(1)(3),···,z(1)(n))为1次 累加生成序列X(1)的紧邻均值生成序列，其中：

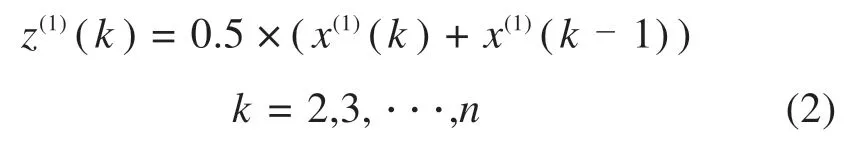
设序列X(0)，X(1)和Z(1)如上所述，称式(3)为GM(1,1)模型的基本形式，也称为GM(1,1)模型的灰色微分方程，这是含1阶方程及1个变量的差分方程。

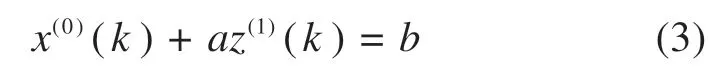
式中：a为模型的发展系数，主要反映x(1)(k)的发展趋势；b为模型的协调系数，主要反映数据间的变化关系。

构造GM(1,1)模型的最小二乘估计参数向量来求解参数a和b，最小二乘估计参数向量β如式(4)所示。

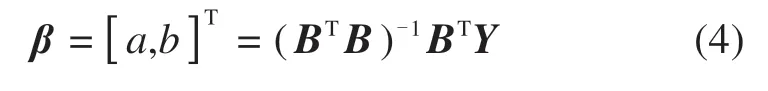
其中：

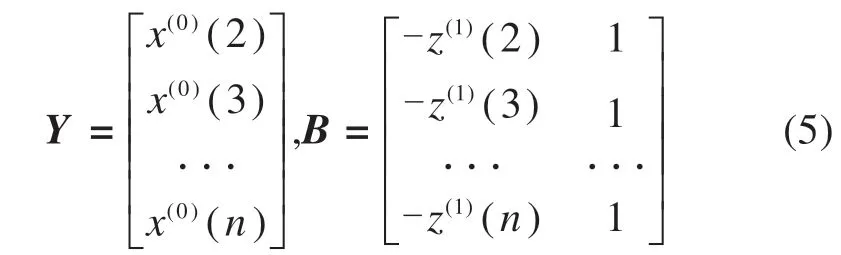
构建GM(1,1)模型的灰微分方程x(0)(k)+az(1)(k)=b的白化微分方程如下：

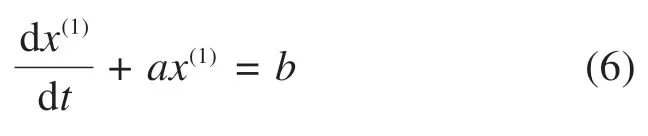
求解式(6)，得GM(1,1)模型时间响应函数如下：

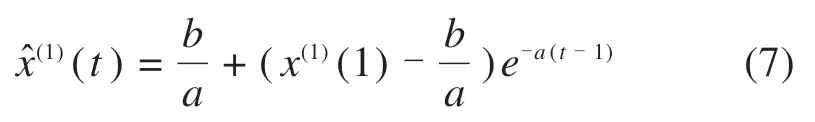
将式(7)离散化，并取初始值x(1)(1)=x(0)(1)，得到累加序列X(1)所对应的预测序列)如下：

对作1阶累减还原，得到的预测方程如下：

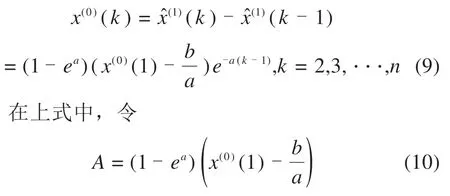
则式(9)可以简化为

2.2 经典模型与优化模型存在的不足

GM(1,1)模型的预测精度受原始序列光滑性的影响较大，如果原始序列光滑性较差，会导致预测值与实际值偏差较大，模型精度较差。在构造模型结构参数时，具有一定的随机性，所构造的参数并不能保证模型的精度最高。

GM(1,1)模型对于系统的规律性描述会随着时间的推移逐渐失真。灰色预测模型是在预测逼近曲线和坐标平面时间轴围成的区域内，通过微分拟合法构建的模型。夹在预测模型上下界之间的灰平面会随着时间的推移逐渐增大，呈漏斗状展开，如图2所示。

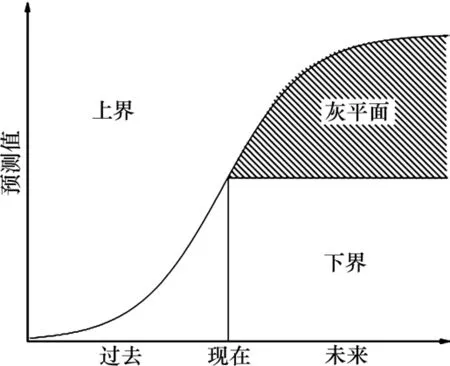
图2 灰色预测模型灰平面Fig.2 Gray plan of the gray prediction model

由图2可知，未来预测值与当前实际值间隔时间越长，灰平面范围越大，预测模型的预测精度越低。由此可见，经典灰色预测模型中能够反映系统客观规律的只是靠近当前时刻的预测数据，距离较远的预测值精度较低，只能用来描述数据序列的变化趋势，参考意义显著降低。

GM(1,1)模型完全依赖模拟结果而忽视预测趋势，往往出现“过拟合”现象，导致预测模型的理论精度与实际精度相差较大。

目前常用的模型优化方法有原始数据预处理和结构参数优化两大类。部分现有优化方法缺少系统性，仅仅是从某一个方面对预测模型进行改进，没有考虑改进模型的整体性和结构参数的相关性。部分模型优化方法脱离实际情况，并没有对研究对象进行灰色预测模型适用性分析。

2.3 综合改进模型的建立

2.3.1 模型改进思路

考虑到经典模型以及现有优化模型存在的不足，在构建道面预防性养护评价指标灰色预测模型时，为了提高预测精度，首先对原始数据进行检验及预处理，提高原始数据的光滑性，然后考虑到改进模型的整体性和结构参数的相关性以及初始值及背景值是相互影响的原因，对预处理得到的数据进行初始值及背景值同步改进，最后为了延伸灰色预测模型的实效范围，提高预测精度，就必须提高模型的白化程度，通过不断补充新信息的方式对当前时刻附近的灰空间进行白化处理，达到缩小模型灰平面的目的。通过这3步优化方法对GM(1,1)模型进行综合改进，进而构建道面预防性养护评价指标的综合改进灰色预测模型(以下简称“综合改进模型”)，具体的改进流程如图3所示。

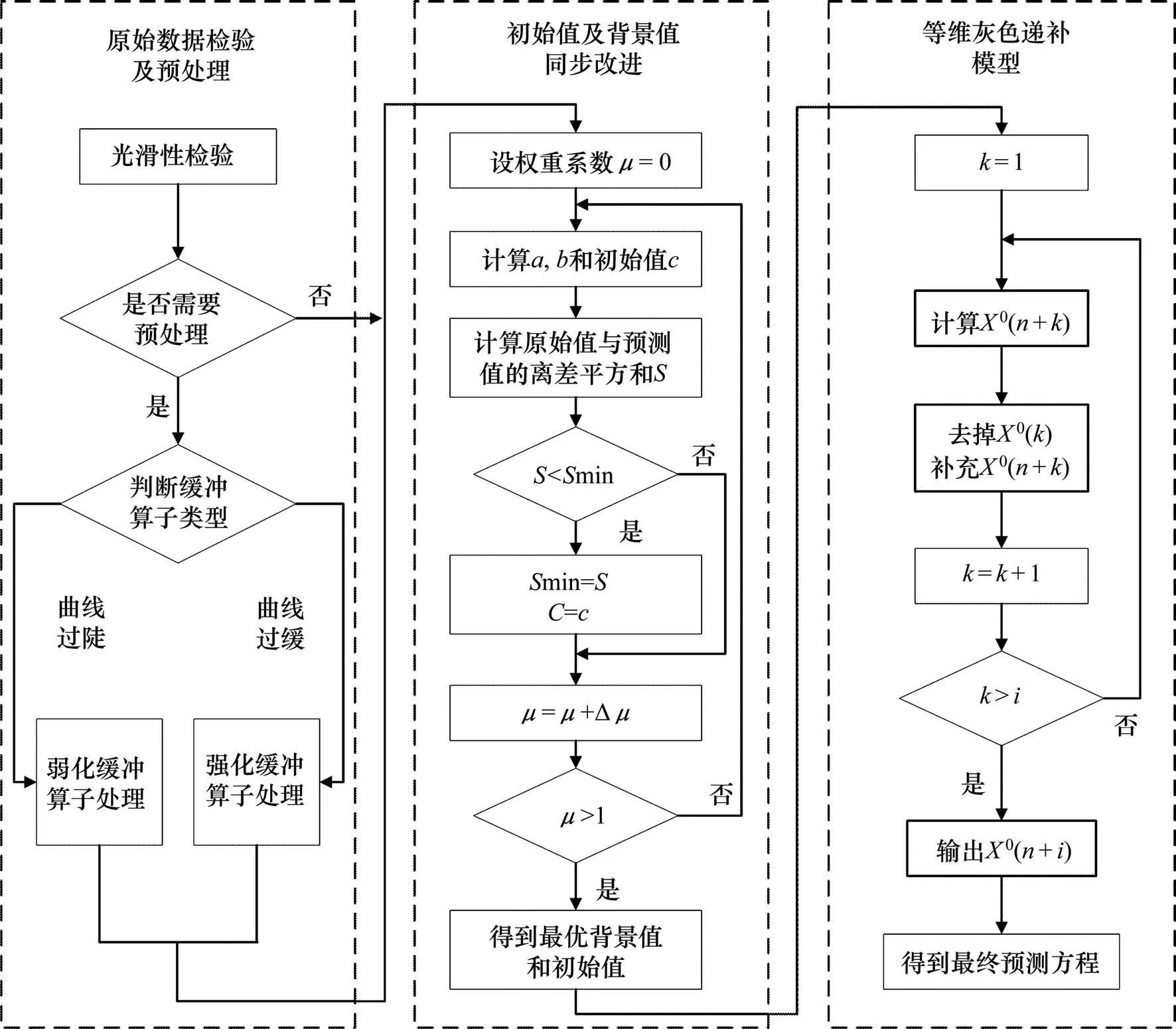
图3 综合改进流程图Fig.3 Integrated improvement flow chart

2.3.2 原始数据检验及预处理

在构建灰色预测模型之前，首先对道面预防性养护评价指标进行光滑性检验。若通过检验，则可以直接采用改进结构参数的灰色预测模型建模。若没通过检验，则必须先对评价指标序列进行预处理，才能保证最终模型的预测精度。本文采用光滑比对原始序列进行光滑性检验。

设原始序列

定义光滑比为：

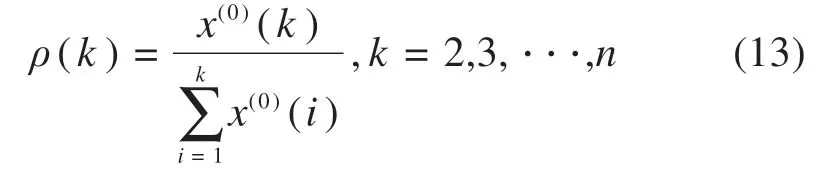
当ρ(k)符合公式(14)中的条件时，序列X(0)可以视作准光滑序列。

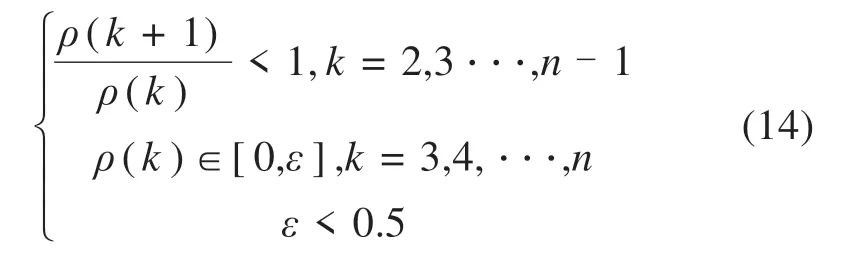
如果检验发现建模序列不满足光滑性要求，必须选择合适的缓冲算子对其进行预处理，使其满足光滑性条件之后再进行建模。

本文采用党耀国等[16]提出的灰色缓冲算子，通过对建模序列进行数据处理，优化建模序列的变化趋势，从而将定性分析结果融入到系统未来发展趋势之中，改善建模序列光滑性，提高模型预测精度。

设原始序列X=(x(1),x(2),···,x(n))，缓冲序列XD=(x(1)d,x(2)d,···,x(n)d)，则定义式(15)为平均弱化缓冲算子，式(16)为平均强化缓冲算子。

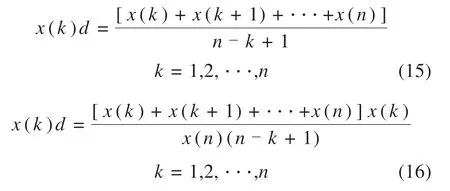
2.3.3 初始值及背景值同步改进

在经典GM(1,1)模型基础上对模型的初始值和背景值进行同步改进，以预测值和实际值的离差平方和作为改进依据，选取离差平方和最小的初始值和背景值作为最终的结构参数，建立初始值及背景值同步改进的灰色预测模型。

首先对背景值z(1)(k)进行改进，令

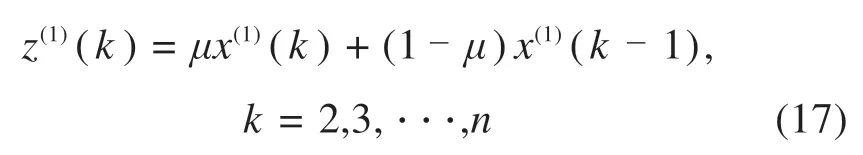
其中：z(1)(k)为改进后的背景值；μ为权重系数，μ∈[0,1]。

利用最小二乘法求解式(3)所表示的灰色微分方程，得出含有权重系数μ的参数a和b。

接着对模型初始值进行改进，继续求解微分方程式(6)，这里初始值不再取x(1)(1)=x(0)(1)，而是用待定常数c来表示，得到时间响应函数如下：

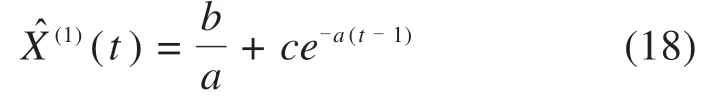
其中：为X(1)序列的预测序列；c为待定常数。将式(18)离散化，得到改进后X(1)的预测序列X̂(1)如下：

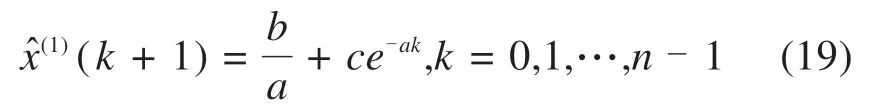
将式(19)累减得到原始序列X(0)的预测序列为：

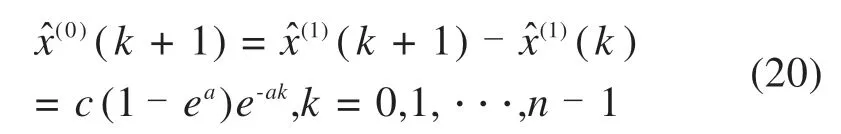
令C=c(1-ea)，将C代入式(19)和式(20)中可得：

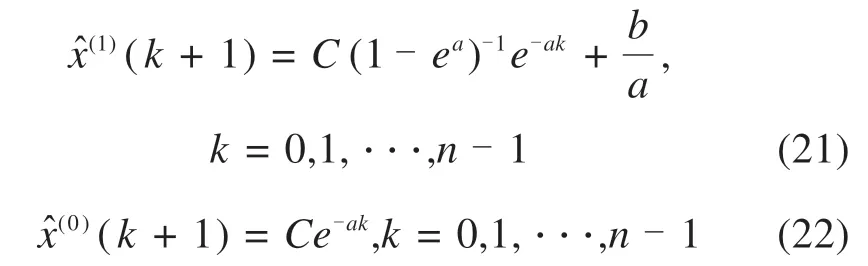
通过预测值与实际值的离差平方和最小来确定待定常数C。

构造预测值与实际值的离差平方和S如下式所示。

将式(22)代入式(23)得：

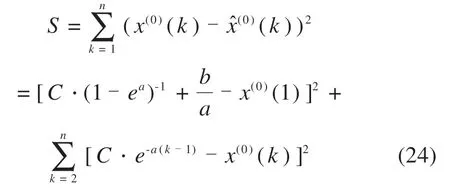
代入式(21)和式(22)可得：

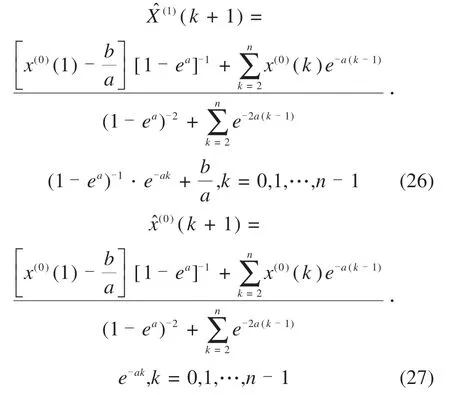
设初始权重系数μ=0，计算该权重下实际值与预测值的离差平方和，然后在此基础上给权重系数μ增加一个微小量Δμ，即μ+Δμ⇒μ，重复该过程，直至μ=1，选取实际值与预测值离差平方和最小的权重μ作为最优权重系数，进而得到该权重下的初始值及背景值，最终采用最优权重系数所对应的预测方程式(27)对数据进行预测。

2.3.4 等维灰色递补模型

鉴于经典GM(1,1)预测精度随着时间推移逐渐降低，距离预测时刻较近时期的信息对于该时期的预测将更有价值。为了提高预测精度，必须对上述优化灰色预测模型进行改进。先利用当前序列建立灰色预测模型获得一个预测值，将该预测值作为已知值补充到建模序列中，同时去掉距离当前时刻最久的数据，建立新的灰色预测模型，以此类推，直至得到目标时刻的预测值为止。具体建模过程如下：

将原始序列X(0)的n个数据组成的序列建立灰色预测模型，通过式(27)预测得到(n+1)，然后将(n+1)作为信息补充到X(0)中，并将X(0)中最老的数据x(0)(1)去掉，形成新的序列如下：

通过新的序列预测得到(n+2)，然后将(n+2)作为信息补充到中，再把中最老的数据x(0)(2)去掉，形成新的序列如下：

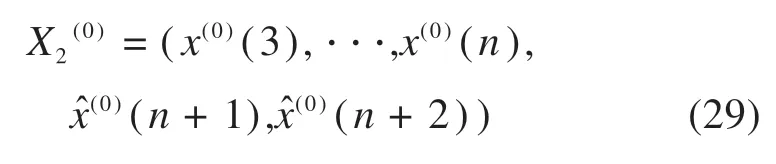
依此类推，可以得到改进后各年的预测值(n+i)。

2.4 模型建立与求解

为了验证综合改进模型的有效性，选取东北季冻区军用机场作为主要研究对象，基于某军用机场道面检测数据，参考周围同类军用机场道面检测数据，采用时间-空间转换的方法，得到该机场连续时间内的道面性能数据。鉴于机场水泥混凝土道面预防性养护评价指标中，道面破损指数与其他指标关联度最大，最具代表性，因此本文选用破损指数为代表对综合改进模型进行检验。选用连续8 a的道面破损指数数据，用于模型精度检验，如表1所示。

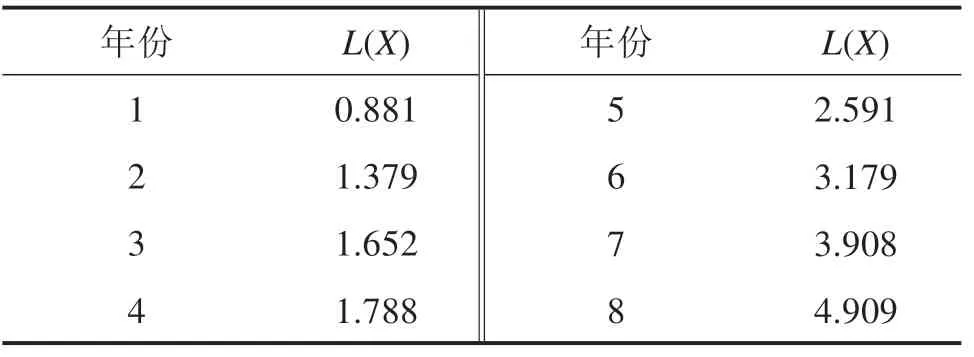
表1 道面破损指数统计表Table 1 Statistical table of pavement damage index

在建立灰色预测模型之前对道面破损指数实测值进行光滑性检测，结果如表2所示。从表2中可以看出第2年之后所有年份的光滑比ρ(k)值均小于0.5，且值均小于1，满足准光滑序列要求，不需要对原始数据进行缓冲算子处理。

表2 光滑性检测表Table 2 Smoothness test table

基于多步改进方法，利用MATLAB软件建立如图3所示的道面预防性养护评价指标综合改进灰色预测模型，并对其进行编程计算。

3 模型精度检验

3.1 模型精度检验方法

模型性能包括模拟性能和预测性能2个方面，本文主要利用相对模拟误差和相对预测误差对模型进行精度检验，在此基础上，选用后验差法进行辅助精度检验，尽可能使预测模型精度符合实际情况。

3.1.1 相对误差法

选取原始序列X(0)前n个数据组成的序列建立灰色预测模型，通过模型计算得到相应的模拟序列和预测序列。

将模拟序列的相对模拟误差序列记为ΔS，即：

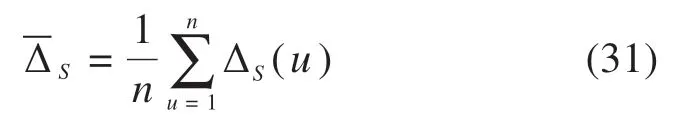
同理，将预测序列F̂(0)的相对预测误差序列记为ΔF，即：

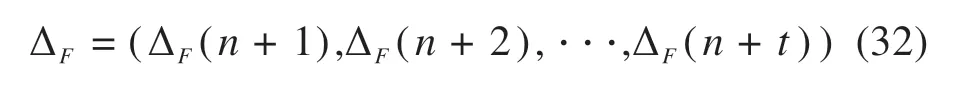
3.1.2 后验差法

后验差检验是根据预测模型的预测值与实际值之间的方差比和小误差概率等统计量进行检验的方法，它是以残差为计算基础，统计残差较小的点出现的概率，以及有关预测误差方差的指标大小，后验差计算的具体步骤可参考文献[17]。其中，指标C和P的取值为C>0，0≤P≤1。方差比C越小越好，C越小说明相比于建模序列离散程度，预测模型得到的时刻残差拟合程度很高。小误差概率P越大越好，P越大，表明残差以较高的概率分布在残差平均值周围。结合C与P2个指标，对预测模型的精度进行评定，具体等级划分可参考文献[17]。

3.2 精度检验

3.2.1 多步改进过程精度纵向对比检验

从道面破损指数原始序列L(x)中选取前5 a的数据，用于创建模型和检测模拟精度，选取后3 a的数据用于检测模型的预测精度，分别采用传统GM(1,1)模型，初始值及背景值同步改进模型以及综合改进模型对道面预防性养护评价指标进行预测，预测结果如表3所示。

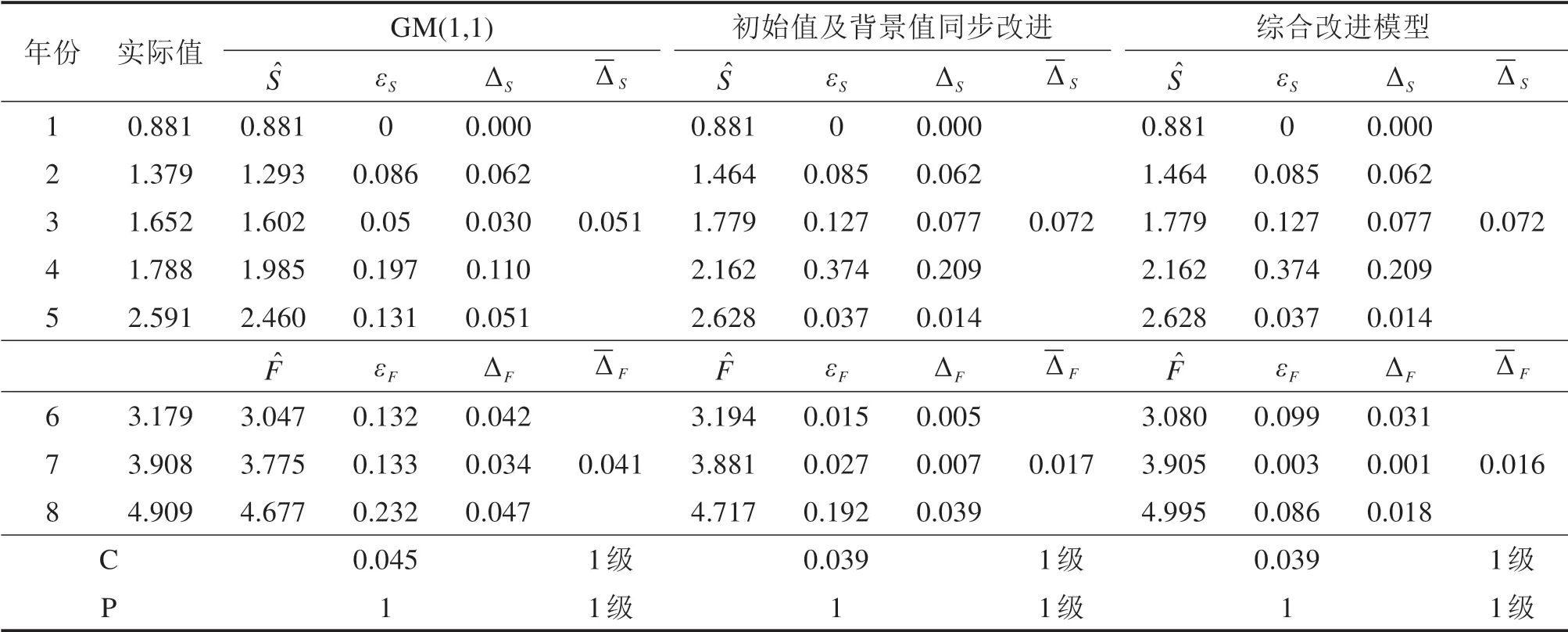
表3 模型预测结果对比分析表Table 3 Comparative analysis table of model prediction results

分析表3可以看出，经典GM(1,1)模型和初始值及背景值同步改进模型的小误差概率P都为1，精度等级为1级，后验差比值C都小于0.35，精度等级也是1级，进一步说明灰色预测模型适应于道面预防性养护评价指标预测。经典GM(1,1)模型的模拟精度较高，但是预测精度较差，出现了“过拟合”的现象。通过初始值及背景值同步改进的方式减缓了经典GM(1,1)模型的增长趋势，改进后的模型更加符合机场道面性能变化规律。从表3中可以看出，初始值及背景值同步改进模型虽然模拟精度不如经典GM(1,1)模型，但是预测精度相比于经典模型有了大幅度提高，并且方差比也有改进，说明综合改进模型可以提高灰色预测模型的精度。在初始值及背景值同步改进模型的基础上，综合改进模型采用等维递补的方法，降低了灰平面，进一步提高了预测精度。因此，综合改进模型达到了提高模型预测精度的目的。

3.2.2 与马尔可夫预测模型的精度横向对比检验

为了进一步验证综合改进模型应用于水泥混凝土道面预防性养护评价指标预测的可行性，进一步检验预测模型精度，将综合改进模型的预测结果同马尔可夫预测模型的预测结果进行对比。这里同样选取道面破损指数作为原始数据，马尔可夫预测模型与综合改进灰色预测模型的精度对照如表4所示。

从表4中可以看出，相比于马尔可夫预测模型，综合改进模型在相对模拟误差、相对预测误差上都有了很大的提高。考虑到军用机场道面检测数据少，且不同地区观测数据异质性较高，导致马尔可夫预测模型很难得到稳定的参数估计或者得到的参数主观性较高。因此，综合改进的灰色预测模型更适合于军用机场道面预防性养护评价指标的预测。

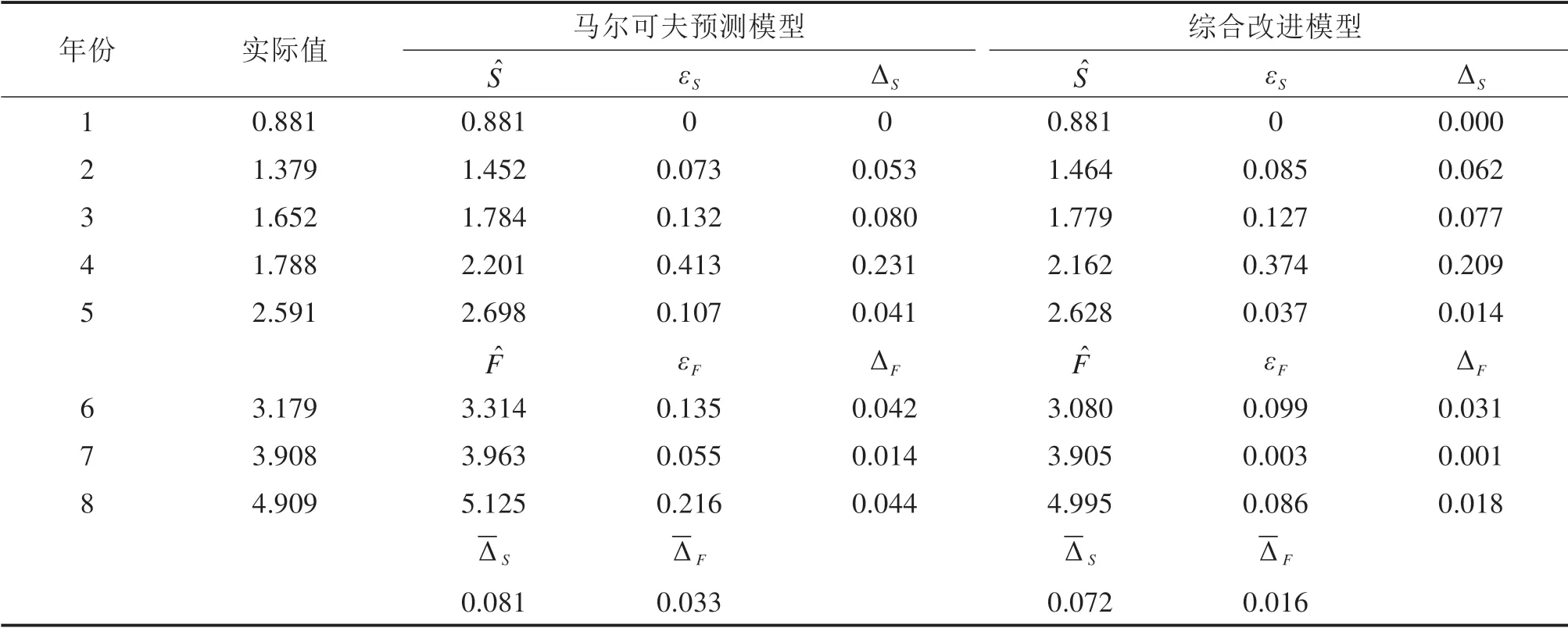
表4 预测结果对比分析表Table 4 Comparative analysis table of forecast results

4 案例分析

根据某军用机场预防性养护的需求，利用时间—空间转换法对机场的道面样本进行道面年龄及指标数据重构，得到了该机场跑道道面各项指标的重构数据。为了确定道面预防性养护的最佳时机，选取该机场第1～5 a的预防性养护评价指标数据作为性能预测的原始数据。采用综合改进模型分别对破损指数、摩擦因数、边角剥落率、表面剥落率、表面裂缝率、板间错台率、国际平整度指数和PCN等8个指标进行预测。通过对综合改进灰色预测模型进行MATLAB编程计算，先对原始数据进行检验与预处理，然后进行初始值及背景值同步改进，最后利用等维灰色递补得到预测结果（如图4所示），可以看出道面预防性养护评价指标之间存在密切的联系，当一种指标达到养护临界值，另外的指标也达到或接近相应临界值，即需要采取预防性养护措施。通过分析各个指标的预测结果和指标养护上下限，确定预防性养护最佳时机。

通过查阅相关资料，得出各个指标预防性养护上下限值，结合图4中各个预防性养护评价指标预测值，可以得出各个指标预防性养护上下限值对应的年限，具体情况如表5所示[11]。

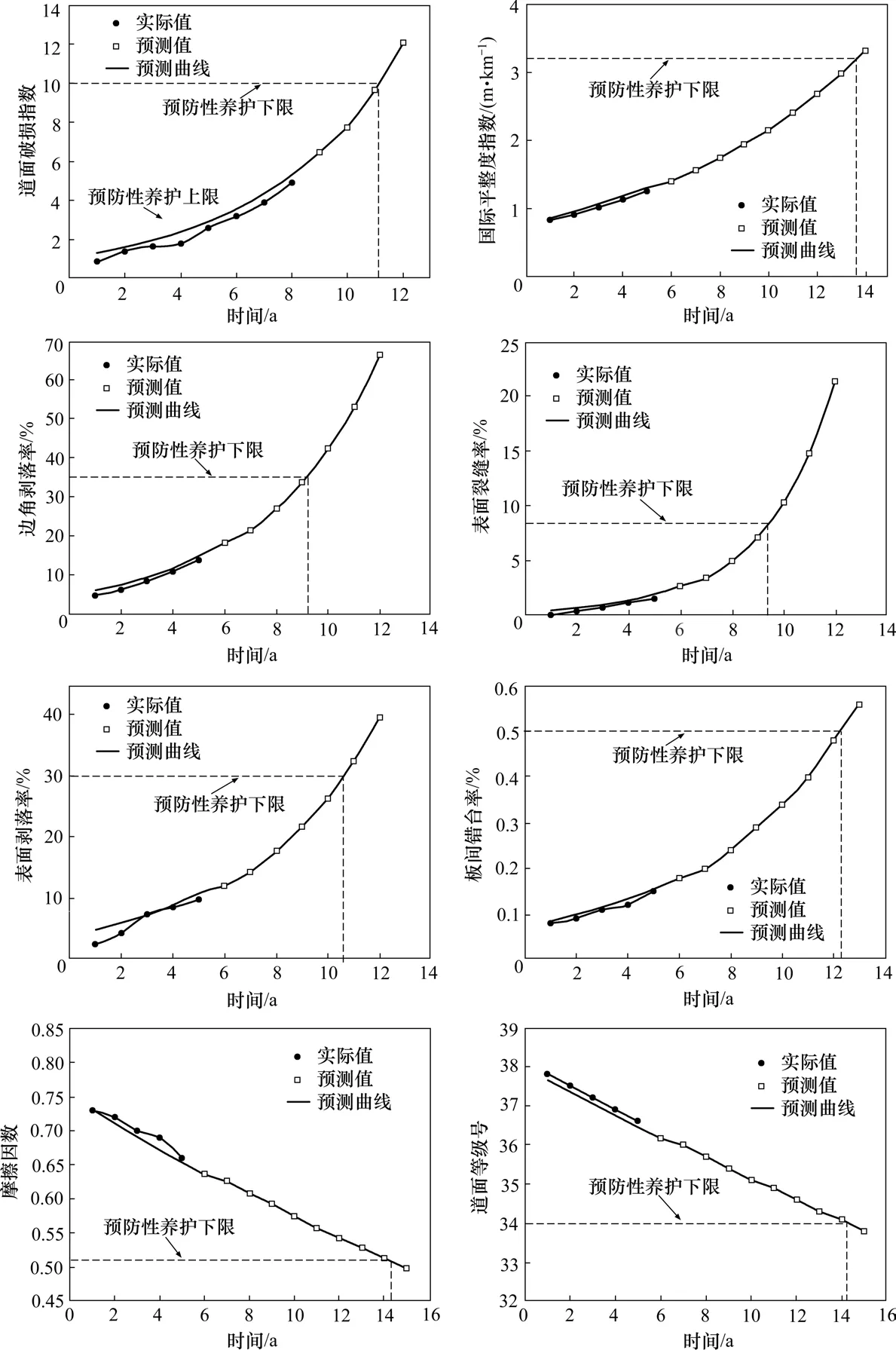
图4 道面预防性养护评价指标预测Fig.4 Prediction of pavement preventive maintenance evaluation index

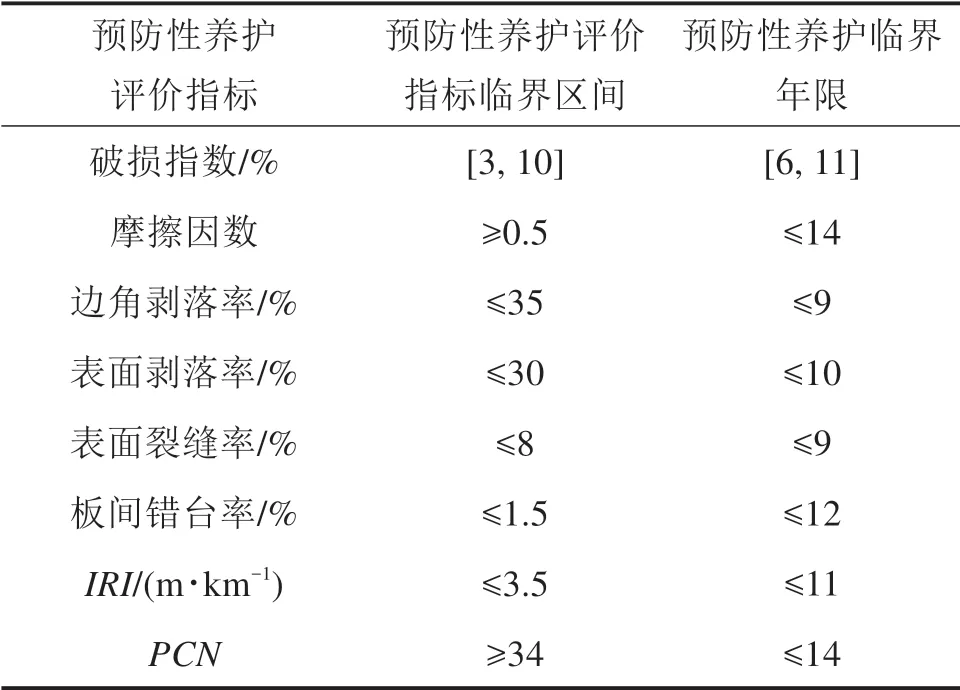
表5 预防性养护评价指标临界年限统计表Table 5 Statistical table of critical age of preventive maintenance evaluation indicators

综合分析表5中各个预防性养护评价指标对应的预防性养护临界年限，基于时间窗的基本理论，计算各个指标所对应的预防性养护时间段的交集，同时考虑到军用机场飞行训练任务的特殊性，得出该军用机场采取预防性养护措施的最佳时机为6～9 a，即预防性养护总时间窗为[6,9]。

采用综合改进的灰色预测模型，可以对全国各个地区的军用机场道面预防性养护指标进行预测，判断出最佳养护时机，便于科学精准地对军用机场采取预防性养护措施，进一步延长军用机场的使用寿命。

5 结论

1)结合军用机场水泥混凝土道面的特点，基于道面性能指标数据少且采集困难的现状，通过适用性分析引入了灰色预测模型；通过分析灰色预测模型以及现有优化方法存在的不足，采用原始数据预处理、初始值及背景值同步改进以及等维灰色递补等方式对经典GM(1,1)模型进行优化改进，构建了水泥混凝土道面预防性养护评价指标综合改进灰色预测模型；经过纵向和横向对比，验证了模型的精度，说明综合改进的灰色预测模型更适用于军用机场水泥混凝土道面预防性养护评价指标的预测。

2)利用综合改进的灰色预测模型对某军用机场的表征道面性能的8个指标进行预测，结合各个指标预防性养护判定标准以及军用机场的特殊性，计算出该机场预防性养护最佳时机为第6～9 a。本文的研究方法和预测模型可为下一步军用机场道面实施精确化预防性养护措施和养护年限提供参考。