计及风险规避的综合能源系统分布鲁棒优化调度

2022-01-20张美金张馨玥才志君

电力需求侧管理 2022年1期

张美金，张馨玥，才志君

（1.辽宁工程技术大学电气与控制工程学院，辽宁葫芦岛 125105；2.国网吉林省电力有限公司检修分公司，长春 130000）

0 引言

为提倡绿色、环保、经济的电力运行，风能、天然气等清洁能源在电网的应用逐渐广泛，由此也带来一些问题，新能源出力的不确定性和不易控性为系统的稳定性带来风险［1］，甚至出现系统崩溃等问题，如风电的反调峰特性使得新能源消纳问题突出，以及出现电网、气网、热网的耦合问题［2］。因此，研究含风电不确定性规避的综合能源系统优化运行对系统经济性和稳定性运行具有实际意义。

目前综合能源系统已成为一种趋势，已有文献对电-热网、电-气网的互联做了研究，也对电-热-气三网互联的系统经济运行和调度以及系统规划做了分析，文献［3］设计了一个综合需求响应（integrated de⁃mand response，IDR）方案，以P2G设备、热泵、多种存储设备和灵活负荷的运行为基础，综合考虑多个系统之间的相互作用，实现了电力、天然气和供热互联系统的优化调度。然而，随着可再生能源装机容量不断扩展及综合能源系统研究的持续推进，风电渗透率对电网的经济运行也带来一定挑战，因此在系统优化运行中有必要规避风电不确定性带来的风险。针对风电不确定性问题，有文献提出随机规划和鲁棒优化的方法，文献［4］提出考虑电-热耦合等约束条件下的鲁棒机组组合模型，使风电消纳问题得到了优化，但由于随机规划和分布鲁棒的保守性，电网经济运行未达到理想效果。随着不确定性问题的研究，逐渐出现新的分布鲁棒方法用于此类问题的研究，文献［5］提出分布鲁棒的实时调度方法，用一阶矩、二阶矩表示风电的不确定分布，并通过重构线性化技术将原模型转换为线性模型，通过简化模型来求解问题。文献［6］在考虑风电场出力与负荷响应量相关性的基础上，建立以成本最小化为目标的日前优化调度模型。除了通过改进模型本身来提高模型的可行性和准确度，还提出一种数据驱动的分布式鲁棒优化模型。文献［7］以集成的燃气-天然气耦合系统为基础，提出了一种数据驱动的分布式鲁棒优化模型，通过大量真实数据参与运算，使结果更精确。由此可见，可行数据的筛选以及风电的不确定性程度，也是决定模型可行性的关键环节，因此需将数据驱动方法与风电模糊集结合来求解优化问题。文献［8］提出一种基于模糊优化集对分析理论的需求侧用户响应潜力评估方法，通过分析影响该模式下用户参与响应的因素，建立用户评估指标体系，但由于仅选取了常规火电机组下与用户响应特性密切相关的核心指标，并未讨论电-热-气综合能源电网以及风电机组的并网对用户需求响应的影响，因此本文将以综合能源系统为背景，考虑风电的不确定性，建立含风电模糊集的系统优化运行模型。

本文所建立的综合能源系统是在计及风电不确定性的基础上，考虑电、热、气3种能源，以电网约束、热网约束和气网约束为条件，加入热电解耦CHP设备、P2G设备和储电、储热装置的互联系统。针对这一系统，提出一种具有风险规避的分布鲁棒优化模型，用条件风险值作为风险测度，表示风电机组出力的不确定性，并用L1范数构建概率分布模糊集，实现综合能源系统的经济运行，改善风电消纳问题，最后通过算例验证和分析不同场景下模型的可行性。

1 综合能源系统结构

综合能源系统是电、热、气3种能源的统一协调系统，具备电、热、气能源的转化和储蓄功能，对风、光剩余的消纳起到一定作用，能够实现能源的经济调度和分配。在电-气耦合和电-热耦合过程中，采用具有P2G技术的设备和热电解耦的CHP设备，通过电、热、气的相互转化，提高能源利用率，优化系统运行。

1.1 P2G技术

P2G技术是电能储存的新思路，同时也为大量清洁能源的储存提供合理方式，能够提高电-热-气互联综合系统的供能稳定性。电转天然气经过两个化学反应过程后产生甲烷和水，转化效率约为45%～60%［9］。P2G数学模型可以由能源转化效率来建立，即

式中：QP2G,i,t为第i个P2G设备在t时段产生的天然气流量；ηP2G为P2G设备的效率；PP2G,i,t为P2G设备的功率；Hgv为天然气热值，取9.883 kWh/m3。

1.2 热电解耦的CHP

CHP的工作原理是利用热回收系统将燃气产电过程中的余热收集并输出热能，提高系统运行效率和经济性能，用热电比表征其效率，即

式中：u(t)为CHP实时热电比；为t时刻CHP的发热功率；为t时刻CHP的发电功率。

热电解耦CHP的结构模型如图1所示。

图1 热电解耦CHP结构Fig.1 Heat⁃electric decoupling structure of CHP

解耦的CHP以低温余热有机朗肯循环（organic Rankine cycle，ORC）系统代替固有CHP的以热定电的运行方式，使发电余热一部分进入余热利用ORC系统产生电能，另一部分被热系统收回直接供热给热负荷［10］。

1.3 综合能源系统结构

综合能源系统主要包括燃气锅炉、电锅炉等类型的常规机组、风机、储电装置，以及P2G设备和热电解耦的CHP设备，结构图如图2所示。

图2 综合能源系统结构Fig.2 Structure of integrated energy system

在该系统中，P2G在谷荷时段将风电转化为天然气，峰荷时段通过CHP的气-电转化来实现削峰填谷。两者的联合调度以容易大量存储的天然气为媒介，协调电源与负荷需求，实现电能的峰谷和时空的补偿，平滑净负荷曲线，缓解高渗透率风电间接拉大负荷峰谷差的问题，提高系统运行可靠性。

2 综合能源系统优化运行模型

2.1 目标函数

综合能源互联系统的优化运行，以系统的总运行成本最小为优化目标，其中包括火电机组、气网的发电和启停成本、CHP模式转换成本和风电场的弃风成本，目标函数表示为

式中：T为一个运行周期的时段总数；f1为常规发电机组发电成本和启停成本总和；f2为系统天然气机组运行成本；f3为CHP模式转换总成本；f4为弃风成本；Np、Ng和Nw分别为系统中火电机组、气源和风电场的数量；c1i、c2i、c3i为运行发电机组的成本比例；PG,i,t为火电机组的有功出力；csti和cspi分别为发电机组的启、停费用；为1表示发电机组状态为开机，为1表示发电机组状态为关机；gj为天然气源的成本系数；Qg,j,t为天然气气源的流量；btran,i,m,n为第i个CHP设备模式转换的启停成本；vn,i,t为第i个CHP设备在n模式下的状态，为1表示模式启动，为0表示模式停止；ξ为弃风惩罚系数；和PW,l,t分别为风机的预测出力和实际出力。

2.2 约束条件

2.2.1 电力网络约束

电力网络约束主要分为电功率平衡约束、电压电流约束、线路功率约束、火电机组出力约束等。

电功率平衡约束为

电压电流与线路功率约束为

式中：Pi,j,t和Qi,j,t分别为输电线路传输的有功、无功功率；xi,j和ri,j分别为线路电抗、电阻参数；Ui,t为节点i电压幅值；Ii,j,t为线路电流幅值。

2.2.2 天然气网络约束

天然气网络模型主要包括天然气气源、管道和储气罐，具体约束如下。

天然气流量平衡约束为

式中：Ng表示天然气系统总的网络节点；Qg,i,j,t为气网节点间的天然气流量；和分别为与节点i连接储气罐的出气流量和进气流量；QGB,i,t为节点i的燃气锅炉所消耗的气源流量；Qg,L,i,t为气网用气负荷；QCHP,i,t为节点i的CHP所消耗的气源流量。

天然气管道流量约束为

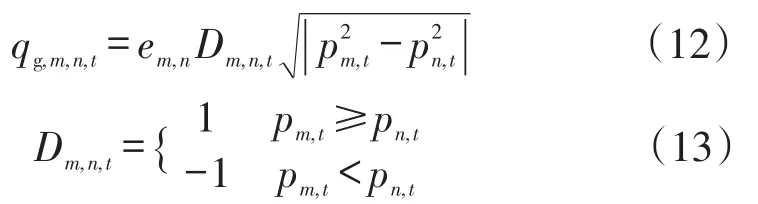
式中：em,n为与管道温度、长度、直径和摩擦系数等因素有关的传输系数；Dm,n,t为管道内天然气流动方向；pm,t和pn,t分别为m管道和n管道在t时段的气压。

供气约束和节点气压约束分别为

式中：qmax,g,m,n和qmin,g,m,n分别为气管道mn的流量最大值和最小值；pmax,m和pmin,m分别为管道节点的气压最大、最小值。

2.2.3 热网约束

在建立的模型中，热能来源于燃气锅炉和CHP机组，约束包括热功率平衡约束、CHP机组的功率约束和热电解耦CHP的约束。

热功率平衡约束为

式中：HGB,i,t为第t时刻第i台电锅炉的供热功率；NCHP为CHP机组的数量；NGB为电锅炉装置数量；HCHP,i,t为CHP机组对系统的供热功率；HL,t为系统t时刻的总热负荷功率；ηGB为燃气锅炉的能源转化效率。

2.2.4 风力约束

风力约束可表示为

3 分布鲁棒优化调度模型

3.1 目标函数

由于电力网和气网的潮流约束都为二次非线性约束，采用二阶锥规划的方法，将其条件松弛后转化成线性规划，便于计算机的运算，加快计算速度。转化前，先对变量定义，令，对电网潮流约束进行松弛变换，得到

则电网-气网潮流的二阶锥标准型为可以写成

根据式（3），可以将此问题的分布鲁棒模型分为两阶段，即外层的主问题和内层的子问题，求出最坏情况下的目标函数最优值，基本模型为

式中：x为第一阶段的决策变量，第一阶段包括发电机组、热电联产机组和电转气设备的启、停成本和各能源的储存成本；X为非空第一阶段问题可行集；EP(·)为求期望函数；c为式（3）的系数向量；Q(x,ω)为第二阶段的最优解，ω为第二阶段的随机变量，要求在发电机组重新优化调度的过程，考虑最坏情况下，对ω不确定风力出力的消纳与储存，使得系统能源消耗最小的最优解；ρ为集合Ω上包含真实概率分布P的分布模糊集。第二阶段模型为

式中：y为第二阶段的决策变量；Y为第二阶段的决策变量可行域，代表式（19）—式（20），是经过二阶锥松弛后的决策变量；q(ω)为考虑风电不确定性情况下与第二阶段决策变量之间的耦合关系；W、T(ω)和h(ω)分别为由式（8）—式（18）确定的向量和矩阵。

3.2 基于风险规避的分布鲁棒优化模型

将式（21）两阶段鲁棒优化的基本模型展开为一般形式［11］

式中：ℛ[•]为风险测度，表示风电出力的X为非空第一阶段问题可行集；λ为风险值的权重大小；为线性关系等式。

在文献［12］中，条件风险值（conditonal value of risk，CVaR）表示为对每个x得到的损失函数L(x,ω)的条件风险值CVaRβ，将此条件风险值作为风险测度，其具体表达式为

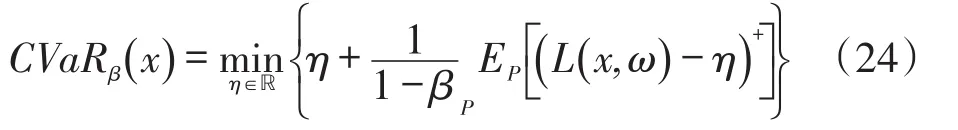
式中：（f）+为取f与0中的较大值；η为风险值。将式（24）代入式（23），用含置信度β的CVaRβ表示式（23）中的风险测度，可得含风险值的两阶段分布鲁棒优化模型为

式中：λ为风险值的权重大小，表示风电出力的不确定性程度，作为控制两阶段分布鲁棒优化结果的变量；β为置信度，限制模糊集的变化范围，作为控制CVaRβ的变量。

3.2.1 构造模糊集

用概率质量p和标称概率质量p0之间的L1范数表示总变差，当Ω是有限集时，基于L1范数的模糊集定义为

式中：p0为标称概率质量，即风电出力的初始概率值，可以基于历史数据进行构建；d为通过数据驱动方法确定的容度，由风电机组出力的历史数据得到，d≥0。由于使用概率密度函数描述风电出力分布，为了使模拟更加精确，因此需要用模糊集对风力的出力分布进行约束，通过控制d的大小，限制模糊集的变化范围。

3.2.2 重构两阶段分布鲁棒优化模型

对每一个ωi∈Ω，有 Probp{ω=ωi}=pi。对于，给定常数d≥0，可以将表示为

由于通过选择d>0，总可以保证存在概率分布P0属于模糊集ρ的内部，即Slater条件（强对偶性的充分条件）成立。因此，可将第二阶段问题描述为

假设p0已知，对于给定的风险值λ∈[0,1]，置信区间β∈(0,1)，令 ℛ(·)=CVaR(·)，基于风险规避的一般分布鲁棒模型（23）等价于式（29）

通过此模型，可以得到第二阶段最恶劣情况下的最优目标函数值。最恶劣情况指弃风率最大且风电机组成本最高情况下的最小综合能源运行总成本，满足此条件。

4 算例分析

4.1 算例系统构成

在IEEE 39节点电力系统和7节点气网系统下仿真。共10台发电机组，总装机容量为6 967 MW，总电力负荷为5 941.5 MW，其中包括6台火力发电机，2台燃气机组，1台CHP热电联产装置，1台P2G设备。

将不同机组组合运行的情况分为以下场景。

场景1：不含P2G设备、热电解耦CHP设备、热储、电储，仅考虑风电不确定性的电力系统经济调度。

场景2：加入热电解耦CHP设备的风电不确定性的电力系统经济调度。

场景3：加入热电解耦CHP设备和P2G设备的风电不确定性的电力系统经济调度。

场景4：加入热储、电储、热电解耦CHP设备和P2G设备的风电不确定性的电力系统经济调度。

场景5：加入热储、电储、热电解耦CHP设备和P2G设备，未考虑风电不确定性的电力系统经济调度。

4.2 仿真结果分析

不同场景下风电机组出力情况如图3所示。由场景2、3与场景1对比得，加入CHP热电解耦装置对供热出力影响较大。加入P2G设备后，风电机组的总出力提升，弃风率得到改善。

图3 各场景下风电机组出力情况Fig.3 Wind turbine output in various scenarios

不同场景下的火电机组出力情况如图4所示，加入热电解耦CHP设备、P2G设备和电储、热储装置后，火电出力减少。

图4 各场景下火电机组出力情况Fig.4 Output of thermal power units in various scenarios

不同场景下的供热出力情况如图5所示，热电解耦CHP设备可以在电负荷很高的时候发挥作用，将燃气机组产生的余热转化为电能以供应负荷，增大了CHP设备电功率输出极限和热能的利用效率。

图5 各场景下供热出力情况Fig.5 Heating output in various scenarios

场景4中的储电和热储装置出力情况如图6所示。在谷荷期即弃风严重期，储电装置储存过剩风电，储热装置放热满足热负荷供电，降低火电机组的出力。在峰荷时期即非弃风严重期，储电装置通过放电满足电负荷，减少火电的出力，提升火电机组的可调节性与灵活性。

图6 场景4中储电和热储装置出力情况Fig.6 The output of power storage and heat storage devices in scenario 4

不同场景下的弃风率以及综合成本如表1所示。通过场景1—4对比可得，加入热电解耦CHP设备和P2G设备能有效减少系统运行成本和弃风率，加入储电和储热设备后，综合成本减少幅度增加。通过场景4和场景5的弃风功率和综合成本对比可得，在加入条件风险值之后，采用模糊集合来约束不确定量，降低模型的保守度，新能源消纳能力在分布鲁棒优化调度的基础上增强，综合成本也得到降低。

表1 各场景下的弃风功率和综合成本比较Table 1 Comparison of abandoned wind power and comprehensive cost in various scenarios

通过验证，可得热电解耦CHP设备、P2G设备以及储电、储热设备和考虑风电不确定性的调度方法增强了电力网运行的灵活性、经济型与环保性，提高了风电消纳能力，降低了弃风率，为新能源消纳提供更多思路，同时降低系统成本，实现经济、绿色运行，验证了系统模型的可行性和有效性。

4.3 不同风险值和置信度下的结果分析

风险值对综合成本的影响如表2所示，风险值越大，表示电力公司承受的有关风电的不确定性风险会变小，此时风电的出力小，对系统稳定运行带来的影响小，主要由常规机组供电满足负荷需求，较风电出力大的情况，运行成本大。当λ的值超过0.5时，对运行成本的影响不再明显，即当风电出力对系统带来的影响可以忽略时，此时运行成本的大小主要受置信度的影响。在进行实际调度时，可以选择适当的风险值，达到最经济的调度方案。

表2 风险值对综合成本的影响Table 2 Effect of risk value on comprehensive cost万元

不同置信度下的综合成本如表3所示，随着置信度增加，运行成本也会增加。我们可以将置信水平解释为系统的安全指数，当置信水平取为80%时，表示系统经济调度过程中最大损失不超过设定值的概率为80%。由于风电出力的不确定性，会使得系统运行总存在一定的损耗，我们可以通过控制置信度来控制损耗的大小，实现系统的最优经济调度。

表3 置信度对综合成本的影响Table 3 Impact of confidence on comprehensive cost万元

不同置信度水平下的VaRβ和CVaRβ的值如表4所示，通过设置不同的置信度值，影响一天系统调度过程中不同设备的运行情况，从而影响综合成本。由表4可知，随着置信水平的增大，VaRβ和CVaRβ的值都会增大，表示系统面临的调度风险增加。随着置信度的不断增大，VaRβ和CVaRβ的增加程度变缓，且VaRβ和CVaRβ之间的差距逐渐缩小。

表4 不同置信度下的VaRβ和CVaRβ值Table 4 VaRβandCVaRβvalues under different confidence levels万元

4.4 不同历史数据下的结果分析

不同历史数据个数下的系统综合成本比较如表5所示。当历史数据增加时，得到的结果越稳定，即结果的概率分布允许偏差减小，模型越不保守，接近于实际运行情况。通过分别设置24 h和72 h的仿真时长，以折算到24 h的系统综合成本为分析对象，可以看出适当延长仿真时间得到的综合成本值波动较小且更经济，输入的历史数据个数越多，效果越明显，验证了模型对系统经济运行的有效性。