我国线性代数教学研究热点分析——基于科学知识图谱的可视化分析

2022-01-20段华斌

湖南科技学院学报 2021年5期

吴争段华斌

吴争段华斌

（湖南科技学院信息工程学院，湖南永州 425199）

针对现有线性代数教学领域的综述研究都是基于传统综述分析方法的现状，以中国学术期刊网络出版总库（CNKI）中2243篇线性代数教学领域期刊文献为数据集，运用科学知识图谱法对线性代数教学领域进行了可视化分析。首先，构建线性代数教学领域的关键词共现图谱，分析了线性代数教学领域的研究方向；然后，绘制了关键词聚类图谱，归纳出我国线性代数教学领域的六大研究热点。

线性代数教学；文献研究；科学知识图谱

当前，世界正处于信息化技术、数字化技术推动的第三次工业革命时期，在此背景下，我国工程教育改革迎来了新的发展。线性代数是一门工科类专业必修的数学基础课程，其传统教学存在知识点过于抽象、教学方法滞后、考核方式单一等问题[1]。为了使线性代数课程达到工程教育认证标准，需要对线性代数教学领域有一个全面而详细的了解，因此，线性代数教学领域的文献综述具有重大意义。

我国虽然已有部分针对高等数学教学的文献研究，例如燕学敏等[2]研究对比了国内外数学思想方法，钱月凤[3]对数学建模在数学教学领域的应用进行了汇总归纳，桂德怀等[4]对高职学院的数学课程改革情况进行了综述分析。但是专门针对线性代数教学的文献综述较少，难以深入反映线性代数教学的独特性。本文运用科学知识图谱法，围绕关键词展开了可视化分析，归纳出线性代数教学研究热点分布情况，为我国线性代数教学提供了借鉴。

本文的组织结构如下：第1节介绍了数据来源及所使用的的研究方法；第2节基于线性代数教学领域的文献构建了关键词知识图谱；第3节归纳出线性代数教学领域的六大研究热点；最后第4节在全文总结的基础上对后续研究进行了展望。

1 数据来源及研究方法

1.1 数据来源

本文从中国知网（China national knowledge infrastructure, CNKI）的期刊数据库中获取文献数据，检索关键词为：主题“线性代数”AND“教学”，检索数据库选择期刊数据库，期刊来源类别为“全部期刊”。共检索到文献2353篇。人工剔除教授风采、期刊简介等非学术性文献后，共有2243篇有效文献。

1.2 研究方法

本文以CNKI期刊数据库中2243篇线性代数教学领域有效文献作为研究对象，以Citespace软件为分析工具。首先，以期刊文献为基础构建关键词共现图谱；然后，在关键词共现图谱的基础上，绘制出聚类知识图谱。通过研读文献，归纳出线性代数教学领域的研究热点。

Citespace是陈超美教授团队基于科学发展模式理论、科学前言理论、结构洞理论、最佳信息觅食理论、知识单元离散与重组理论开发的一款分析科学文献潜在知识脉络的软件[5]。本文使用的软件版本是CiteSpace5.7 R4，软件参数设置如下：时间分区跨度为1992-2020，时间切片选择1年，节点类型为Keywords，提取对象的方法为Threshold Interpolation，（c，cc，ccv）设置为（2，2，20）、（3，2，20）、（3，2，20），以对数似然率算法算法提取聚类标签，以寻径算法对网络进行裁剪。

2 关键词知识图谱

2.1 关键词分布

关键词是论文研究主题的高度概括，是学术文献的核心。本文通过分析线性代数教学研究相关论文的高频关键词及其共现关系，揭示线性代数教学领域的研究热点的分布及历史演变情况[4]。截至至2020年12月31日，CNKI期刊数据库中收录的线性代数教学领域文献共有2638个关键词，平均而言，每篇文献有4个关键词。线性代数教学改革研究领域中有1895个关键词仅出现1次，有313个关键词出现了2次，111个关键词出现了3次，出现次数不超过3次的关键词占总数的87.91%，如表1所示。可见在线性代数教学领域的文献中绝大部分的关键词都是低频次的，这表明线性代数教学研究主题的具有极强的广泛性，同时在研究深度上有待加强。

表1 关键词分布

2.2 关键词共现图谱

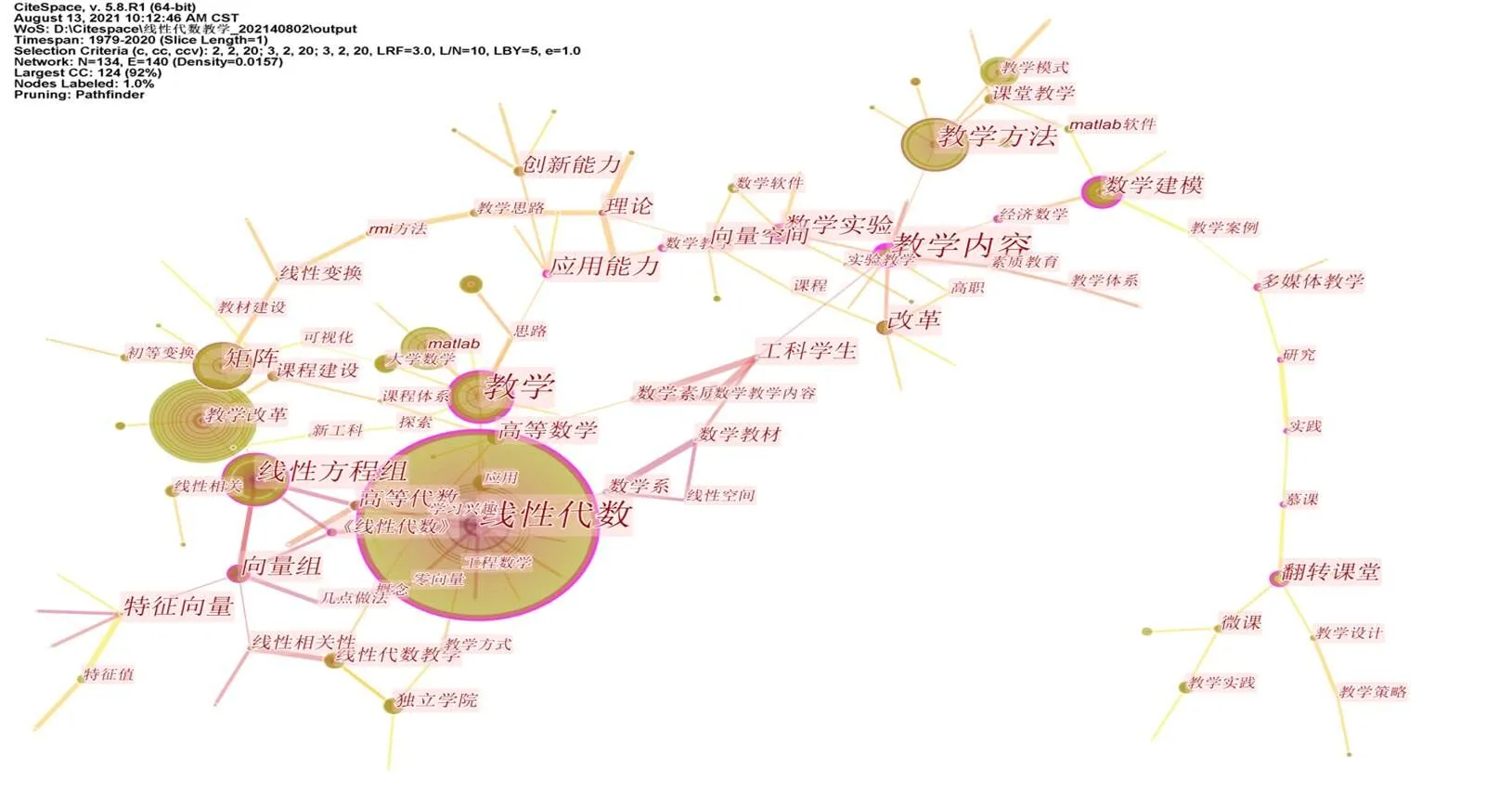
图1 线性代数教学研究关键词知识图谱

以线性代数教学领域的2243篇有效文献为数据，以Citespace5.7 R4软件为工具，构建了关键词共现知识图谱，如图1所示，并且得出线性代数教学领域关键词的频次和中介中心度，部分数据如表2所示。在知识图谱中，关键词的总频次表现为节点大小，如果关键词在共现网络中具有较大影响力，则相应节点具有紫色的外圈，此时称该节点的中介中心度较高。不同关键词之间的关系强弱则通过节点之间的连线（links）反映。

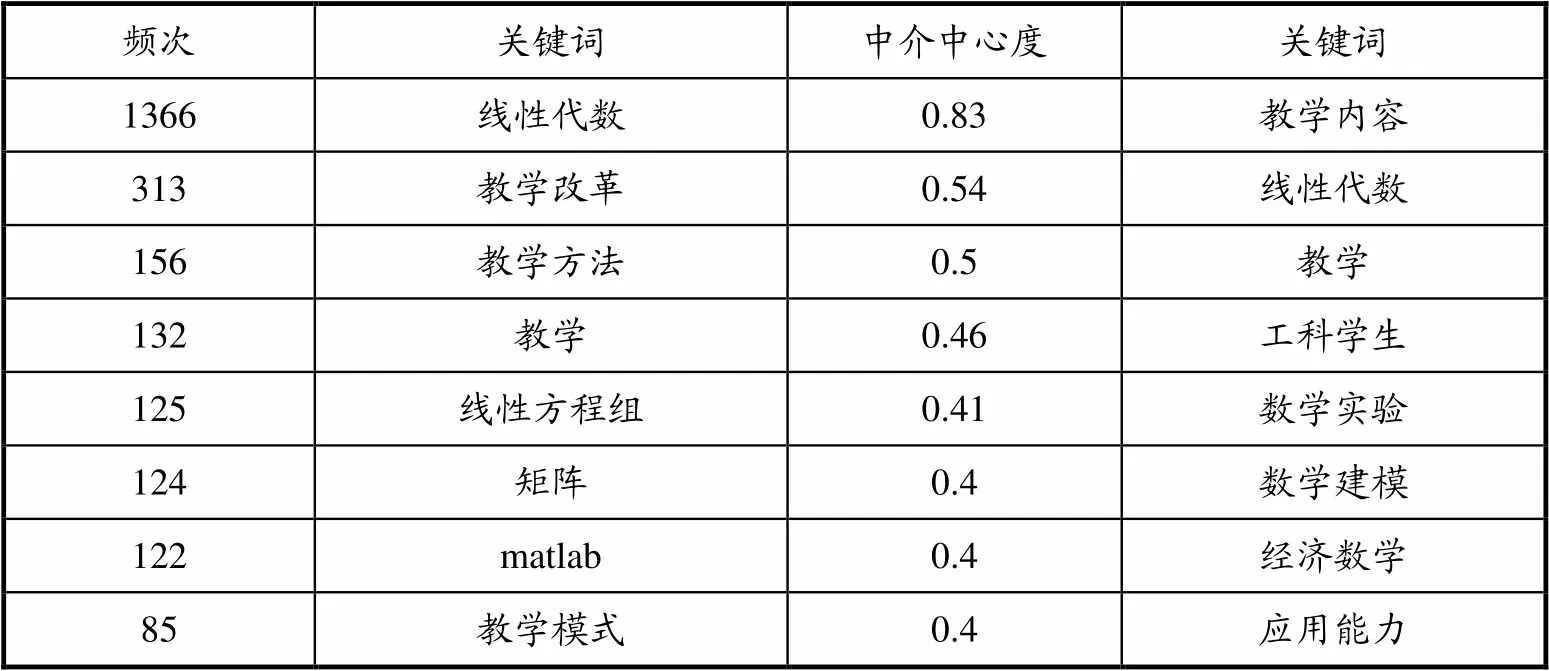
表2 部分关键词的频次与中介中心度

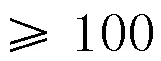
2.3 关键词聚类图谱

使用Citespace5.7 R4的快速聚类功能，绘制线性代数教学领域关键词聚类知识图谱如图2所示，聚类具体参数如表3所示。图2中的Modularity = 0.7833、Silhouette = 0.9387，表明科学知识图谱中聚类结构具有很高的信度。

图2 关键词聚类知识图谱

表3 聚类参数

3 研究热点

结合图2和表3所得，通过研读线性代数教学领域文献，本文将线性代数教学领域的研究热点归纳为6个，并给出每个热点的具体情况：

1）最大的聚类#0，包含18个关键词，Sihouette值为0.921，主要包含改革、教学内容、数学实验、数学软件、教学现状等关键词。居余马[6]提出工科数学教学的内容和体系建设，要为培养面向世界、面向现代化、面向未来的工程技术人才的服务，教学内容要做到从一般到具体的循环渐进。在国际上线性代数教学大致分为两类，以法国为代表的欧洲国家线性代数教学内容以公理化为重心，先线性空间再矩阵，最后教授线性方程组的求解；而美国的线性代数教学截然相反，以矩阵为导向，偏重计算技巧，将计算机技术融入线性代数教学[7]。

2）聚类#1，包含17个关键词，Sihouette值为0.978，主要围绕线性方程组、线性代数、向量组、教学内容、应用型人才等关键词。对于具体教学内容进行改革，借用具体知识点的教学案例，分析知识点之间的衔接，让学生掌握学习的方法，一直是线性代数教学改革总的重要研究领域[8]。

3）聚类#2，包含14个关键词，Sihouette值为1.000，主要围绕翻转课堂、微课、教学设计、慕课、教学实践等关键词。随着信息化技术与互联网技术的飞速发展，结合信息化技术的线上课题已经成为教学改革的热门方向。如何利用新媒体理论，使基于互联网技术的网络授课与传统的课堂教学相结合，是疫情背景下的教学研究新热点[9]。

4）聚类#3，包含13个关键词，Sihouette值为0.910，主要围绕教学方法、数学建模、教学模式、案例教学、课题教学等关键词。线性代数知识的抽象性一直是线性代数教学改革重点关注的问题，尝试将数学建模和案例教学融入线性代数教学，是解决这一难题的主要方向[10]。朱佳俊等[11]尝试将编程实践融入线性代数教学，将抽象的问题与具体案例结合，用问题驱动的方式对教学内容进行安排。赵瑞等[12]给出了一种以数学建模思想为底层逻辑，加速学生综合实践能力养成的教学方法。

5）聚类#4，包含12个关键词，Sihouette值为0.989，主要围绕教学、matlab、行列式、大学数学、辅助教学等关键词。大量教学研究表明，数学软件与数学实验可以有效强化学生对于抽象概念的理解，辅助线性代数教学效果[13]。Matlab以高效矩阵运算、完备的结果可视化、丰富的应用工具箱等优势成为线性代数辅助教学的首选数学软件[14]。

6）聚类#5，包含12个关键词，Sihouette值为0.917，主要围绕教学思路、理论、RMI方法、矩阵、RMI模型等关键词。将先进的教学思路和理论融入线性代数课程教学当中，也是线性代数教学改革的一个方向。单娴[15]将CDIO理论用于线性代数教学，建立了一套循环渐进培养学生理解基础数学知识，掌握自主学习、团队协作、实践创新等能力的教学体系。杨贤仆[16]将“分”与“合”的辩证观点运用于教学，从思想上进行分析，并从具体的表示规律上进行总结，强化了学生在学习线性代数中发散思维的训练与培养。徐海静[17]认为在教学中重视矩阵思维，不仅可以加深学生对线性代数基础知识的理解，还可以达到了教学内容的高度统一。