带锥约束DC复合优化问题的ε-对偶间隙性质

王梦丹 曾方青

带锥约束DC复合优化问题的-对偶间隙性质

王梦丹 曾方青

（湖南科技学院 理学院，湖南 永州 425199）

引入新的约束规范条件，等价刻画带锥约束的DC复合优化问题与其Lagrange对偶、Fenchel-Lagrange对偶问题之间的-对偶间隙性质，推广了前人的部分相关结论。

最优化理论广泛用于工程设计、交通运输、国防等重要领域，具有重要的学术价值和应用前景。同时，很多优化问题都可以看成复合优化问题或者DC优化问题的特例，因此，近年来受到了广大学者的广泛关注。很多学者研究了复合优化问题和DC优化问题的对偶理论、Farkas引理、KKT条件，以及鲁棒分析等[1-9]。2010年，Dinh等[1]利用闭性条件建立了带锥约束的DC优化问题的零对偶理论。方东辉等[5-6]通过共轭函数的下卷积以及函数的近似次微分，给出了复合优化问题的零对偶理论。2019年，在函数不一定下半连续，集合不一定是闭集的条件下，Tian等[7]通过引入新的约束规范条件，建立了DC复合优化问题与其Lagrange对偶问题之间的弱对偶、零对偶、强对偶理论。

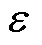
1 记号和定义

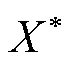
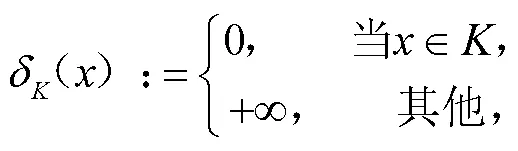
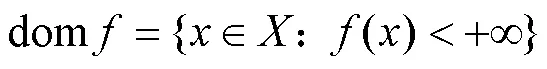
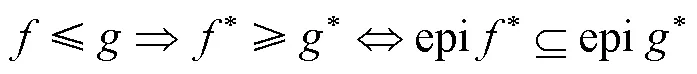
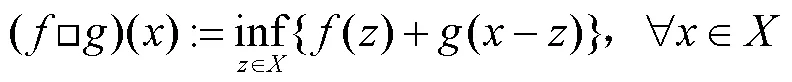
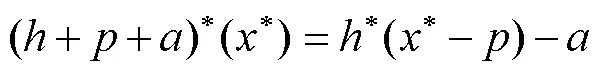
2 主要结果

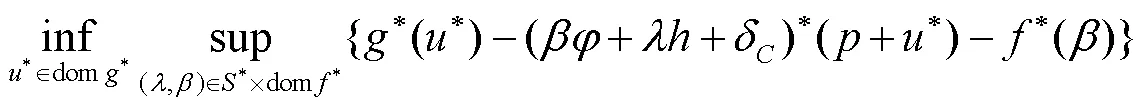
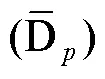
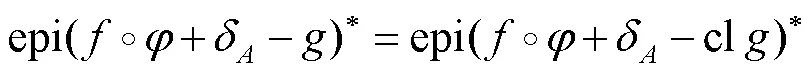
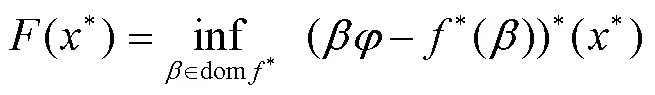
由下端卷积定义可得

从而，

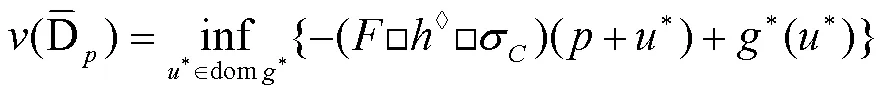
为了简便起见，我们记

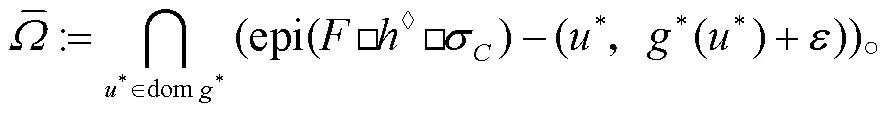
为了研究对偶间隙性质，引入如下约束规范条件：

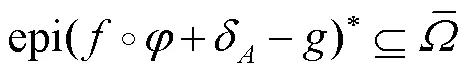
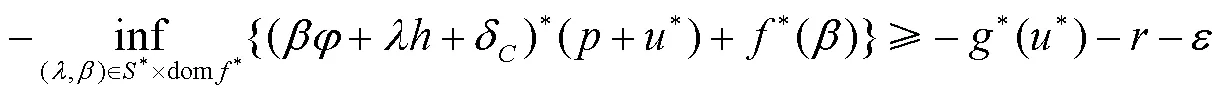
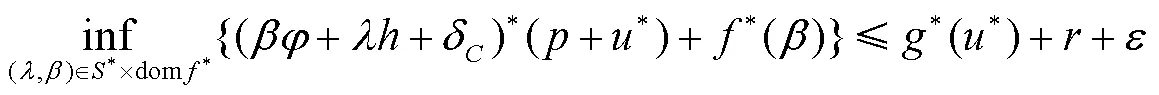
式(6)等价于

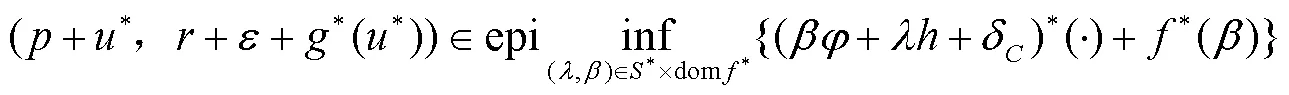
因此，

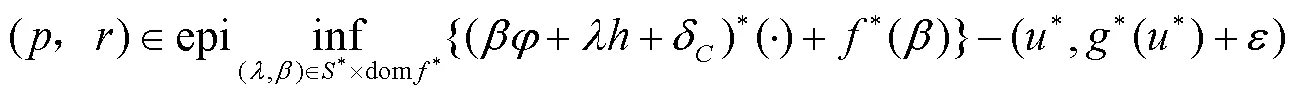
而文献[11]利用

[1]DINH N, NGHIA T T A, VALLET G. A closedness condition and its applications to DC programs with convex constraints[J]. Optimization, 2010, 59(4):541-560.

[2]FANG D H, LI C, YANG X Q. Stable and total Fenchel duality for DC optimization problems in locally convex spaces[J]. SIAM Journal on Optimization, 2011, 21(3):730-760.

[3]AN L T H, TAO P D. The DC (difference of convex functions) programming and DCA revisited with DC models of real world nonconvex optimization problems[J]. Annals of Operations Research, 2005, 133:23-46.

[4]DINH N, MORDUKHOVICH B S, NGHIA T T A. Qualification and optimality conditions for DC programs with infinite constraints[J]. Acta Mathematica Vietnamica, 2009, 34(34):125-155.

[5]FANG D H, ANSARI Q H, ZHAO X. Constraint qualifications and zero duality gap properties in conical programming involving composite functions[J]. Journal of Nonlinear and Convex Analysis, 2018, 19(1):53-69.

[6]方东辉,王梦丹.锥约束复合优化问题的Lagrange对偶[J].系统科学与数学,2017,37(1):203-211.

[7]TIAN L P, WANG M D, FANG D H. Zero duality gap properties for DC composite optimization problem[J]. Journal of Nonlinear and Convex Analysis, 2019, 20(3):513-525.

[8]BOT R I, GRAD S M, WANKA G. Generalized Moreau-Rockafellar results for composed convex functions[J]. Optimization, 2009, 58(7):917-933.

[9]FANG D H, WANG X Y. Stable and total Fenchel duality for composed convex optimization problems[J]. Acta Mathematicae Applicatae Sinica, English Series, 2018, 34(4):813-827.

[13]LONG X J, SUN X K, PENG Z Y. Approximate optimality conditions for composite convex optimization problems[J]. Journal of the Operations Research Society of China, 2017(5):469-485.

[14]LONG X J, XIAO Y B, HUANG N J. Optimality conditions of approximate solutions for nonsmooth semi-infinite programming problems[J]. Journal of the Operations Research Society of China, 2018(6):289-299.

[15]FANG D H, ZHANG Y. Extended Farka's Lemmas and strong dualities for conic programming involving composite function[J]. Journal of Optimization Theory and Applications, 2018,176(2):351-376.

O224

A

1673-2219（2021）05-0011-05

2021-01-08

湖南科技学院应用特色学科建设项目资助（2021）；湖南科技学院科学研究项目资助（21XKY037）；湖南科技学院科学研究项目资助（20XKY063）。

王梦丹（1991－），女，湖南祁阳人，硕士，助教，研究方向为最优化理论研究。曾方青（1993－），女，湖南永州人，硕士，助教。

（责任编校：宫彦军）