偶次平均间断有限元单元内部超收敛点结构

郑玉军 华玉春 汤 琼

偶次平均间断有限元单元内部超收敛点结构

郑玉军1华玉春1汤 琼2

（1.湖南科技学院 理学院，湖南 永州 425199；2.湖南工业大学 理学院，湖南 株洲 412007）

在常微分方程数值解法中，间断有限元法不仅具有高精度，而且对解的光滑性要求较低。考虑常微分方程初值问题的偶次平均间断有限元，在数值计算的基础上研究了单元内部的超收敛点结构及影响因素。

常微分方程初值问题；偶次平均间断有限元；超收敛点；结构

常微分方程初值 问题广泛出现在科学技术、经济等领域中，它有多种数值求解方法，如Euler法、Runge-Kutta法等差分法和有限元法[1-6]。近年来广泛关注的间断有限元法不仅具有高精度，而且对解的光滑性要求较低，因此可应用到求解波动方程与热传方程问题。本文考虑常微分方程初值问题的偶次平均间断有限元[3-6]，在进行了数值计算的基础上研究了单元内部的超收敛点结构及影响因素。

1 偶次平均间断有限元格式

考虑如下问题

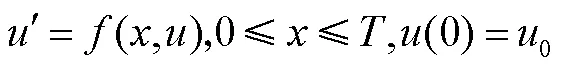
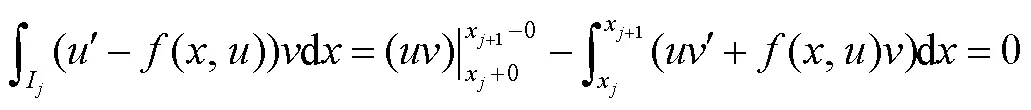
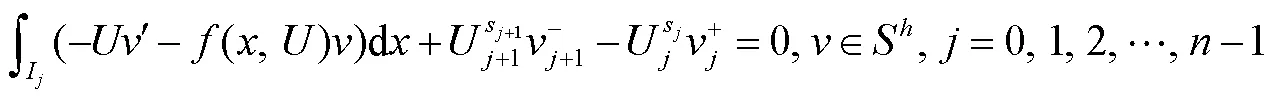
2 偶次平均间断有限元单元内部超收敛点结构

图1、3、5、7、9、11为偶次平均间断零次元误差图，图2、4、6、8、10、12为偶次平均间断二次元误差图，图2、4、6、8误差的量级为10−4，图10误差的量级为10−5，图12误差的量级为10−3。可见，偶次平均间断二次元比零次元精度高些。

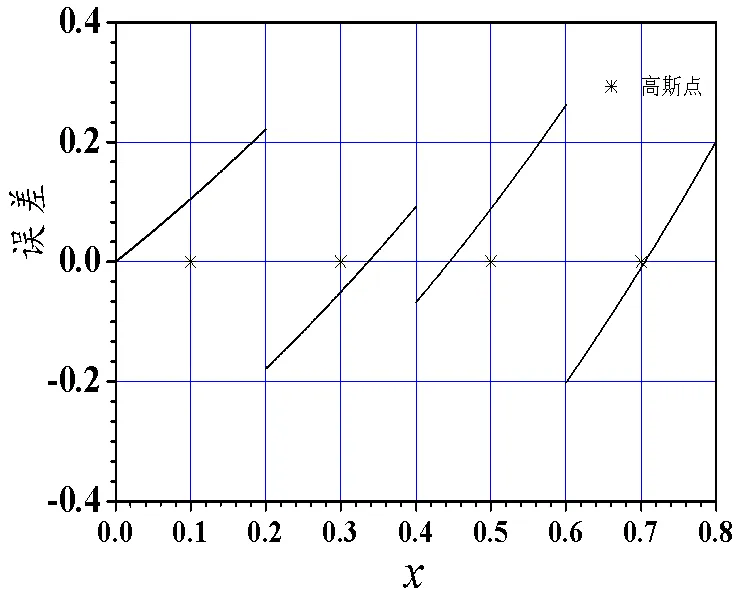
图1 例1的零次元误差

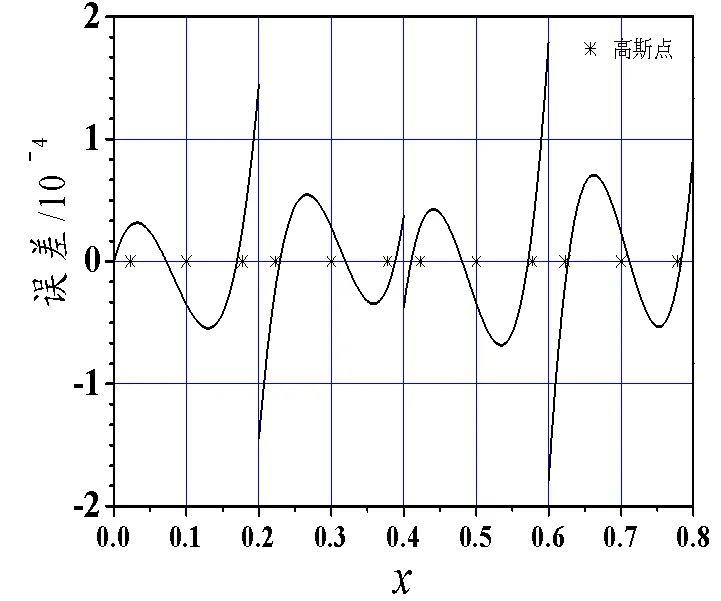
图2 例1的二次元误差

图3 例2的零次元误差

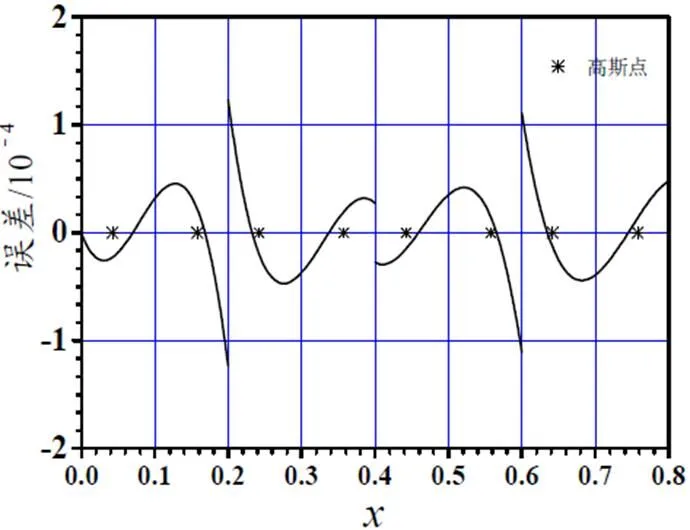
图4 例2的二次元误差

图5 例3的零次元误差

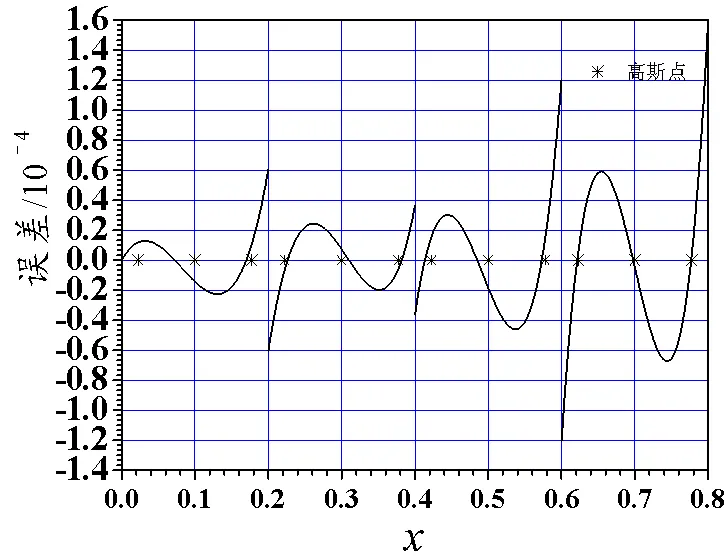
图6 例3的二次元误差

图7 例4的零次元误差

图8 例4的二次元误差

图9 例5的零次元误差

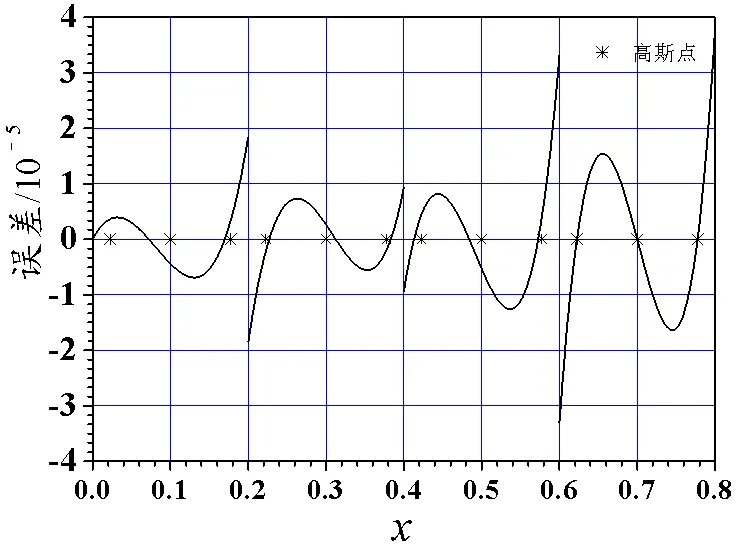
图10 例5的二次元误差

图11 例6的零次元误差

图12 例6的二次元误差

观察4剖分下十二个误差图。例1、3、5的二次元误差图在远离起点的几个单元之后，单元上误差曲线与三次Legendre多项式相当接近，零点与图中的三阶Gauss点非常接近；例1、3、5的零次元误差图，单元上误差曲线与一次Legendre多项式相当接近，每单元内有一个零点。例2、4、6的二次元误差图在远离起点的几个单元之后，单元上误差曲线与二次Legendre多项式相当接近，零点与图中的二阶Gauss点*非常接近；而例2、4、6的零次元误差图，每单元内没有零点。文献[5-6]表明这些Gauss点*是超收敛点。

为探讨单元内部超收敛点的结构与哪些因素有关，改变初值。

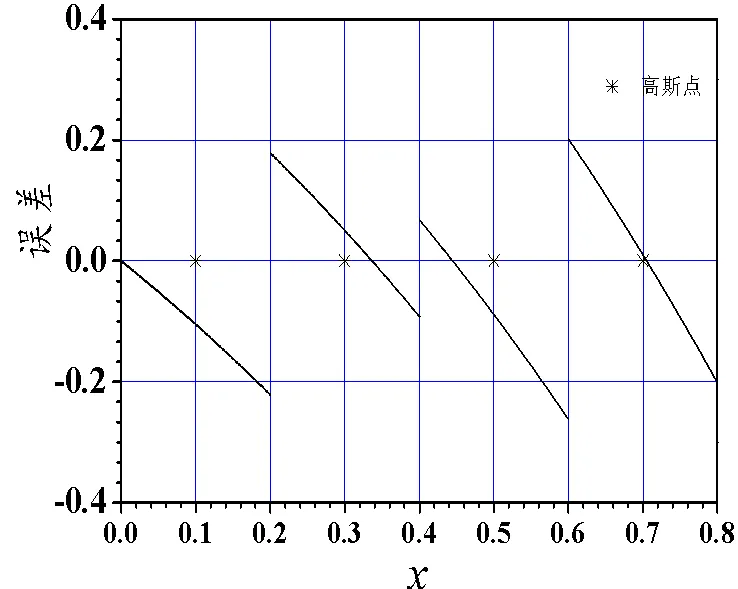
图13 例的零次元误差

图14 例的二次元误差

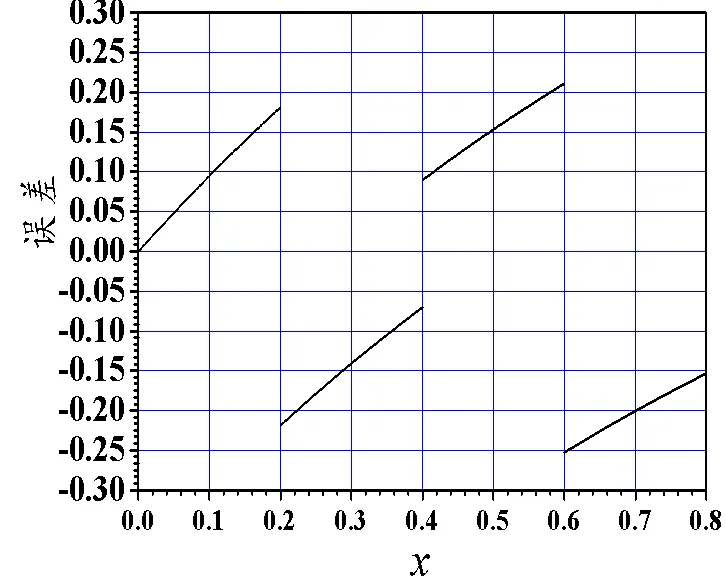
图15 例的零次元误差

图16 例的二次元误差

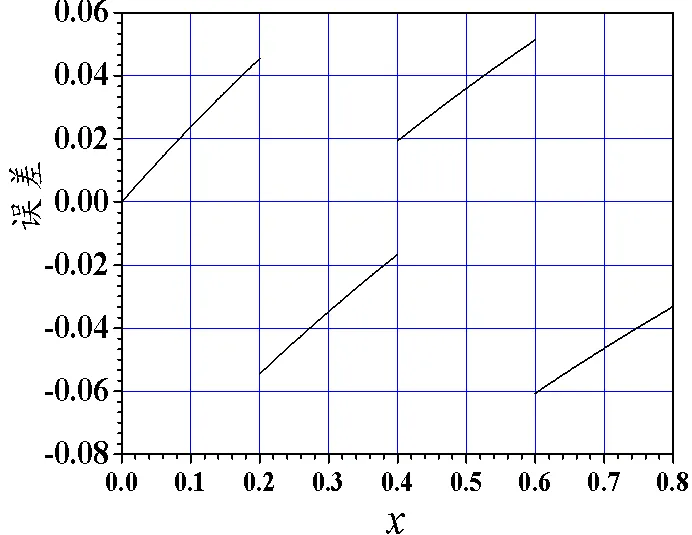
图17 例的零次元误差

图18 例的二次元误差

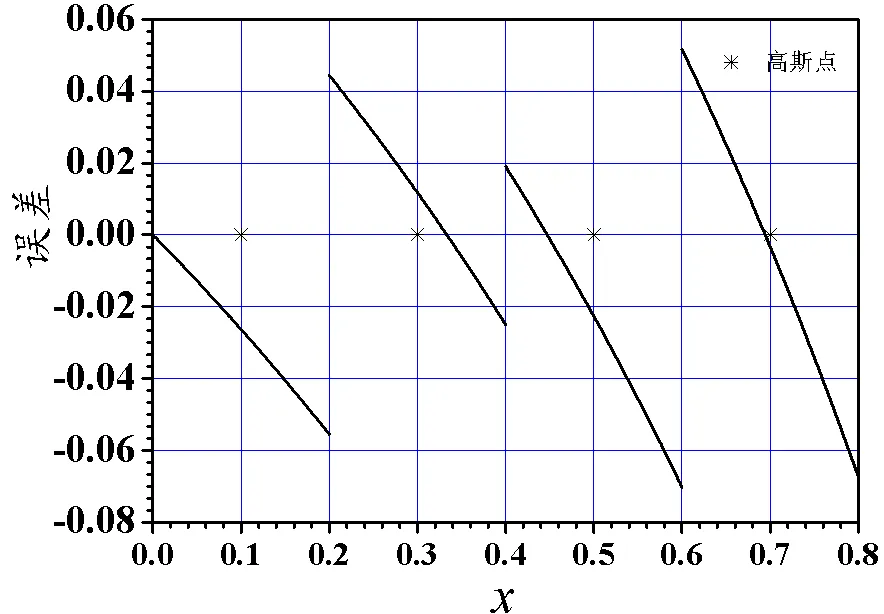
图19 例的零次元误差

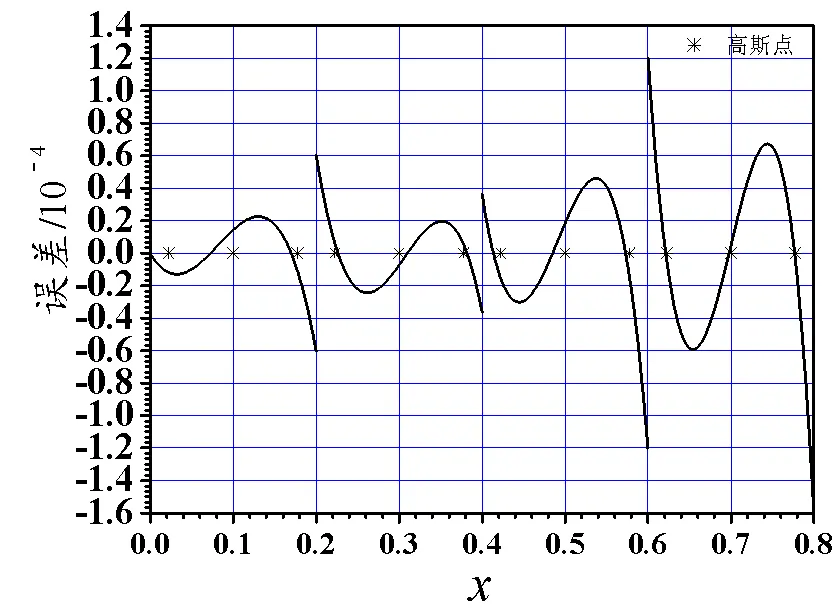
图20 例的二次元误差

表1 单元内部超收敛点个数

[1]陈传淼.有限元超收敛构造理论[M].长沙:湖南科学技术出版社,2001:19-255.

[2]陈传淼.科学计算概论[M].北京:科学出版社,2007:11,138-159.

[3]Delfour M, Hager W, Trochu F. Discontinuous Galerkin methods for ordinary differential equations[J]. Mathematics of Computation, 1981, 36(154):455-473.

[4]李灿华.常微分方程的一类强间断有限元法[D].长沙:湖南师范大学,2006.

[5]郑玉军.常微分方程初值问题的一类间断有限元[J].湖南科技学院学报,2011,32(8):11-12,18.

[6]郑玉军,陈传淼,汤琼.非线性常微分方程初值问题的偶次平均间断有限元[J].延边大学学报(自然科学版),2012,38(4):270-274.

O241.8

A

1673-2219（2021）05-0007-04

2021-03-13

2018年湖南科技学院科学研究项目（18XKY063）；2020年度湖南省自然科学基金面上项目（2020JJ4323），2020年度湖南省教育厅科学研究项目（20A211）；2020年湖南科技学院科学研究项目（20XKY059）。

郑玉军（1982－），男，湖南永州人，硕士，讲师，研究方向为计算数学。

（责任编校：宫彦军）