一类特殊形式的定积分极限问题

赵艳辉 邓春红

一类特殊形式的定积分极限问题

赵艳辉 邓春红

（湖南科技学院 理学院，湖南 永州 425199）

根据函数在一点连续和在一点可导的定义，利用可积(连续)函数的有界性和定积分的分部积分法分两种情形对一类特殊形式的定积分极限问题进行研究，得到被积函数在一点连续或在区间上连续时此类极限问题的极限值与区间某一端点的函数值的关系及被积函数在区间(二阶)可导或某点可导时此类极限问题的极限值与区间某一端点的函数值的关系，为此类极限的计算提供了理论依据，并通过具体实例进行了验证。

数列极限; 定积分; 连续函数; 可积性; 可导性

在数学专业的研究生考试和数学竞赛中经常出现一类与定积分有关的数列极限问题，其中定积分的被积函数为(−)f ()，()是抽象函数。由于此类问题主要牵涉到数列极限定义、函数的连续性、函数的可导性和函数的可积性等重要知识，可以说是一元函数微积分重要知识的综合运用，因此研究此类问题的解法不仅可以有效巩固所学知识、找到各知识之间的内在本质联系，起到举一反三、触类旁通的作用，而且可以培养学生严谨的数学思维能力，学会用数学思维的眼光分析问题和解决问题。

关于数列极限和函数极限的求法一般的高等数学教材或数学分析教材介绍得非常详细[1-4]。而对于含有定积分的极限问题却鲜有讨论[5]。本文根据函数在一点连续和在一点可导的定义，利用可积（连续）函数的有界性和定积分的分部积分法分两种情形对一类特殊形式的定积分极限问题进行研究，得到被积函数在一点连续或在区间上连续时此类极限问题的极限值与区间某一端点的函数值的关系及被积函数在区间（二阶）可导或某点可导时此类极限问题的极限值与区间某一端点的函数值的关系，为此类极限的计算提供理论依据，并通过具体实例进行验证。

1 函数f (x)在闭区间端点连续的情形

结论1 (i)设函数()在[，]可积，且在=连续，则有

(ii)设函数()在[，]可积，且在=连续，则有

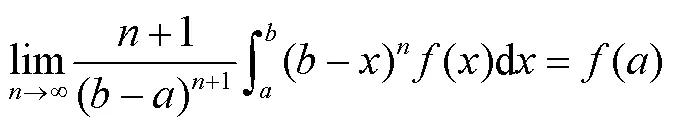
所以有

(5)

所以任给>0，存在自然数，当>时，有

从而由式(5)得：任给>0，存在自然数，当>时，有

同理可证式(2)成立。结论1得证。

当已知函数()在一点连续或在区间连续时，可根据被积函数表达式的特征，利用连续函数的定义及积分区间的可加性将积分区间[，]分成两个小区间[，]和[，]，注意在两个小区间上()−()的处理方式是不同的。如果函数()在区间[，]连续，上述结论自然成立。

将()写成定积分表达式的形式后，可以对绝对值里的表达式进行运算，同时也体现了数学的和谐统一美。

因为积分值不能直接求得，且极限值已知，所以可考虑用数列极限的定义来处理问题。

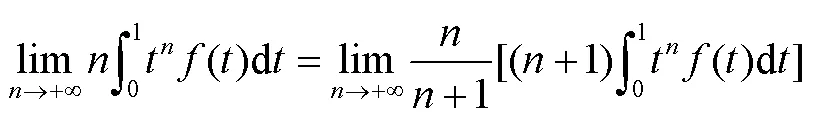
2 函数在闭区间有二阶及以上连续导数的情形

为方便起见，以二阶连续可导为例进行证明。

结论2 (i) 设函数()在[，]二阶连续可导，则有

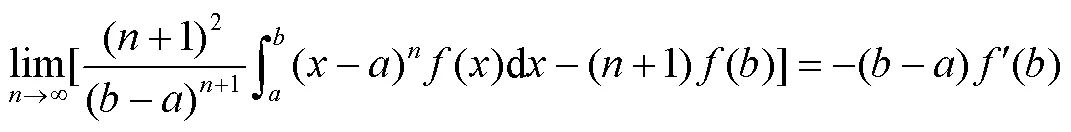
(ii) 设函数()在[，]二阶连续可导，则有

证明：只证结论2中的(i)。依题意，由定积分的分部积分法有

从而有

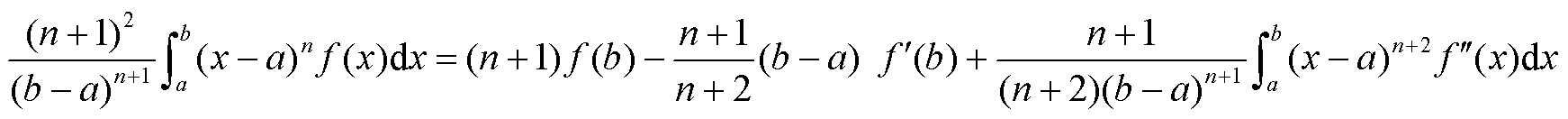
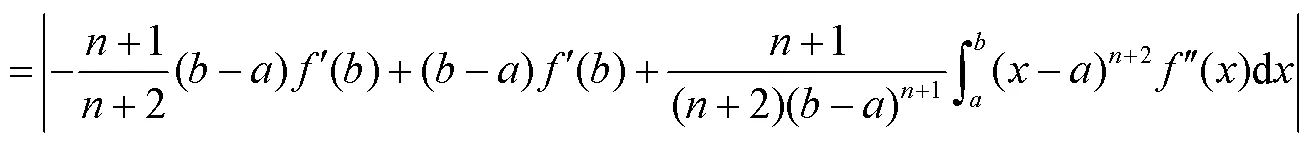
则

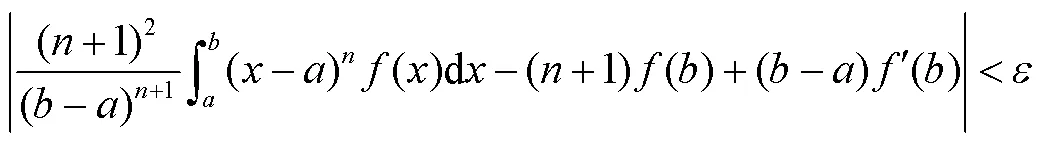
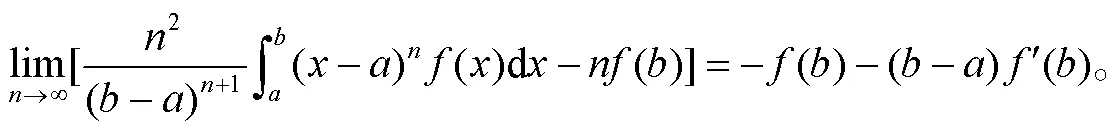
从而式(7)成立。同理可证式(8)和式(9)成立。结论2得证。

例2 设函数()在区间[0，1]上二阶连续可导，求证：

即结论成立。

当函数有二阶及以上的导数时，通常利用带Lagrange余项的Taylor展开式表示此函数，由于导函数具有介值性，所以也不需要导函数连续，利用导函数的介值性处理中值点的导函数值，从而能顺利计算定积分。当已知函数在一点一阶可导时，通常根据函数在一点可导的定义将函数表示出来，只是要注意讨论积分时区间的分割法，以及在不同的区间内积分的不同处理方式，最后求出相应的数列极限即可[6]。

3 结 语

在结论1和结论2中，当积分区间为[，]，被积函数含有()时，极限值与()或()有关，由例1和例2可知。在学习中遇到类似的极限时，可以根据题中所给的条件，如某区间内的可导性、可积性、连续性等条件，结合定积分的性质、函数的连续性、函数的可导性，去分析该类极限的问题。对于与定积分有关的极限问题，如果出现了一点的函数值，通常要将该函数值用相应区间上的定积分形式表示出来，不仅便于讨论，更体现了数学的和谐美以及数学的分类思想。

[1]贺电鹏.极限求法的探讨[J].河南教育学院学报(自然科学版),2017,26(2):44-51.

[2]李东方,谢小军.泰勒公式在求极限中的应用举例[J].科技经济导刊,2018,26(19):175.

[3]李金媛.求数列极限的几种常用方法[J].数学学习与研究,2018(18):6.

[4]华东师范大学数学系.数学分析:上册[M].4版.北京:高等教育出版社,2010:57-64,130-136.

[5]胡丽平.含有积分式的函数的极限[J].天中学刊,2008(5):116-117.

[6]杨学凤,邓秋芳,徐惇儒,等.一类与定积分有关的数列极限问题[J].课程教育研究,2020(8):227.

O172.2

A

1673-2219（2021）05-0003-04

2020-07-07

湖南省自然科学基金面上项目（2019JJ40089）；湖南科技学院应用特色学科建设项目(数学)；湖南科技学院校级一流线下课程建设项目。

赵艳辉（1969－），女，湖南益阳人，硕士，教授，研究方向为多复变函数论。

（责任编校：宫彦军）