纤维织物超高速碰撞热-力学模型与分析

张 祎,王玉林,石景富,于 东,徐铧东,马付健,宋 迪,苗常青

(1.哈尔滨工业大学特种坏境复合材料技术国家级重点实验室,哈尔滨 150001；2.中国运载火箭技术研究院,北京 100076；3.哈尔滨工业大学机电学院机械设计系,哈尔滨 150001；4.中国空气动力研究与发展中心,绵阳 621000;5.电子科学大学机械与电气工程学院,成都 611731)

0 引 言

纤维织物具有较高的比强度、比模量,并且抗冲击性能优异,可柔性折叠,在航天器空间碎片防护方面应用日益增多,如国际空间站密封舱采用纤维织物制成的填充式Whipple防护结构[1-4],Bigelow充气式太空舱采用纤维织物作为其空间碎片防护层[5]。

航天器在轨运行过程中,会受到空间碎片的超高速碰撞,导致被毁伤乃至破坏。在空间碎片超高速碰撞下,航天器防护结构或防护层不仅会产生变形、侵彻、破碎等力学现象,还会产生剧烈的温升、相变及热软化等热学效应[6-9]。

近年来,超高速碰撞热效应的研究受到了越来越多的重视[10-13],但其研究主要集中于传统的金属防护结构,研究发现,热效应不仅会对其力学性能产生显著影响,还会进一步影响其超高速碰撞特性及碎片防护性能[14-15]。受限于实验测试手段的不足[16-17],目前,主要采用数值模拟方法开展超高速碰撞热效应问题的研究,如Povarnitsyn等[12]、唐密等[13]的研究中,采用Johnson-Cook模型模拟了铝板在超高速碰撞过程中产生的碎片云的物相演化及热-力学特性。

纤维材料防护结构或防护层在超高速碰撞下,也会产生剧烈的热效应。目前,对纤维材料超高速碰撞的研究,主要集中于碰撞过程的力学行为和现象,而对其热效应的研究尚未见有文献发表。

对纤维碰撞过程中力学行为的实验研究,是目前纤维材料超高速碰撞研究的主要手段[18-20],研究发现,Spectra纤维与Kevlar纤维织物制成的防护结构,比传统的铝板防护结构具有更加优异的防护性能[19]。纤维结构防护性能与其对弹丸的破碎能力密切相关,不同纤维材料的防护结构对超高速弹丸的破碎能力有显著不同,研究表明,芳纶纤维织物对弹丸有更好的破碎能力[20]。

目前,对纤维结构超高速碰撞力学行为的模拟研究也日益增多,在模拟中,其材料模型主要采用弹性或弹塑性本构模型[21-24],如Shimek等[22]、徐铧东等[23]采用弹塑性本构模型,考虑纤维织物的纱线编织结构,建立了纤维织物超高速碰撞数值模型,模拟其超高速碰撞过程。刘滨涛等[24]基于最大失效应力准则,采用线弹性的正交各向异性本构模型,并考虑纤维织物的纱线编织结构,分别建立了弹丸的SPH模型和纤维织物的FEM模型,模拟得到了纤维织物的超高速碰撞特性及穿孔特征。可以看出,目前对纤维织物超高速碰撞的模拟研究中,纤维材料本构模型主要建立在弹性或弹塑性等纯力学本构关系基础上[25],没有考虑纤维材料的温度、生热等热效应相关的参量,因此,目前对纤维织物超高速碰撞的模拟研究无法分析超高速碰撞过程中的热效应问题,也无法得到其生热、温度场等热学信息。

综上所述,航天器结构在超高速碰撞过程中具有显著的热效应,其热效应对航天器结构的超高速碰撞特性和防护性能有显著影响,目前,对金属结构超高速碰撞中热效应的模拟研究日益增多,但对纤维织物结构超高速碰撞的研究,目前还主要是针对力学行为,尚未有热效应研究的文献发表。为开展纤维织物超高速碰撞过程中的热-力学综合效应研究,本文建立了纤维织物超高速碰撞热-力学单胞数值模型,并分析了碰撞过程中的应力、应变及温度场等热-力学特性。

1 纤维织物超高速碰撞热-力学单胞模型

本文引入Johnson-Cook本构模型及Gruneisen状态方程描述纤维材料的热-力学本构关系,考虑纤维织物纱线编织结构,建立了基于SPH-FEM耦合算法的纤维织物超高速碰撞热-力学单胞模型。

1.1 纤维材料模型

目前,纤维织物超高速碰撞数值模拟中,其材料模型主要是单纯的力学本构模型,如弹性、弹塑性本构模型等,考虑纤维织物在超高速碰撞过程中的热效应,本文引入了Johnson-Cook本构模型[27-28]及Gruneisen状态方程[29]。Johnson-Cook本构模型及Gruneisen状态方程适合具有固定熔点的金属材料,并能够反映应变率强化效应和温度软化效应对材料屈服应力的影响。对于芳纶(对位)、超高分子量聚乙烯等纤维材料来说,其分子链排列规整、取向作用显著、结晶度高且具有较为确定的熔点,故本文采用Johnson-Cook本构模型[28]及Gruneisen状态方程描述纤维材料的热-力学本构关系。

在弹丸冲击作用下,纤维内部静水压力与内能和体积的关系可用Gruneisen状态方程表示为：

(1)

式中:p为静水压力;ρ为密度;e为内能;Γ是Gruneisen参量;η为材料压缩率,压缩为正,拉伸为负。pH为Hugoniot曲线函数上某点的压力值,下标“H”表示Hugoniot曲线函数：

(2)

式中:常数a0,b0,c0可通过线性冲击波速-物质速度关系式求得,该速度关系式为：

Us=Cs+SsUp

(3)

式中:Us为冲击速度；Cs为物质粒子速度；Up为冲击速度与粒子速度的线性相关常量；Ss为斜率。a0,b0,c0计算如式(4)所示：

(4)

其中,ρ0为材料的初始密度,纤维屈服应力Y可用Johnson-Cook模型表示为：

(5)

(6)

1.2 FEM-SPH耦合算法

超高速碰撞数值模拟算法主要采用光滑粒子流体动力学方法(SPH)、有限元法(FEM)等[30-32]。本文综合考虑碰撞过程中弹丸与纤维织物的相互作用,及其破碎、碎片云扩散等问题,采用有限元-光滑粒子流体动力学方法(FEM-SPH)耦合算法模拟弹丸与纤维织物的超高速碰撞问题。首先,对纤维织物几何模型使用FEM法划分网格,在碰撞初始阶段,单元尚未失效时,采用FEM单元,可以模拟超高速碰撞过程中弹丸与纤维织物的纤维束之间的相互作用。其次,在碰撞导致纤维或弹丸失效时,将碰撞失效后的单元转化为相应的光滑粒子,从而可进一步利用SPH方法模拟超高速碰撞导致的弹丸及纤维织物的破碎,及破碎后产生的碎片云特性[33]。

1.3 纤维织物单胞模型

在纤维织物材料模型基础上,基于FEM-SPH耦合算法,针对平纹织物编织结构,建立了纤维织物的单胞模型。为简化分析,织物纤维束的截面形状近似为椭圆形,沿纤维方向的纤维束形状近似为正弦曲线。纤维织物结构及单胞模型如图1所示。

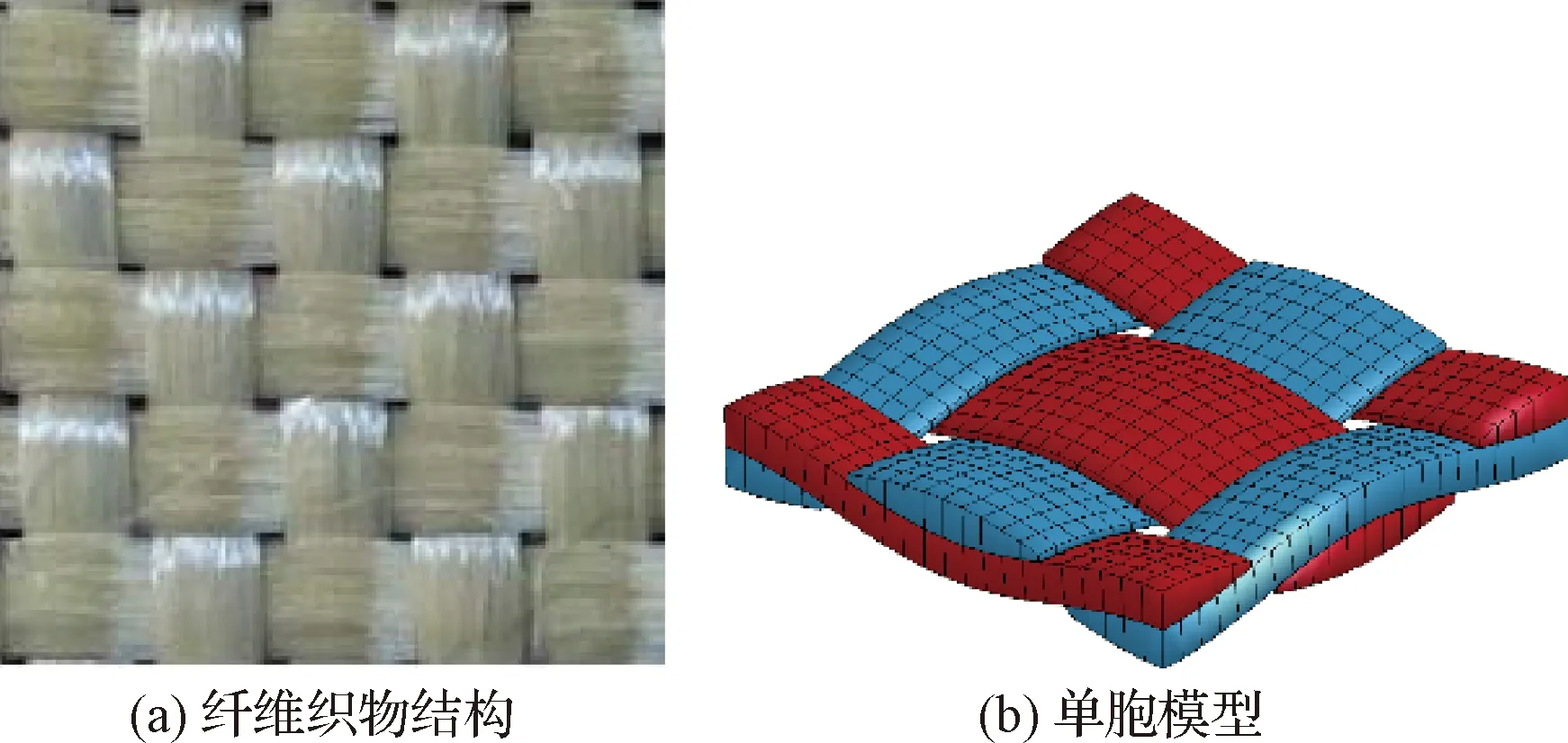
图1 纤维织物结构及单胞模型Fig.1 Fiber fabric structure and unit-cell model

2 纤维织物超高速碰撞热-力学特性分析

本文选取Kevlar49纤维织物作为研究对象,Kevlar纤维是一种高强、高模的聚合物纤维材料,目前已广泛应用为航天器结构材料,并在航天器空间碎片防护方面有一定应用。文献[25]针对Kevlar49纤维进行了力学特性实验研究,分别测量得出了不同应变率下Kevlar49纤维力学特性参数,见表1。

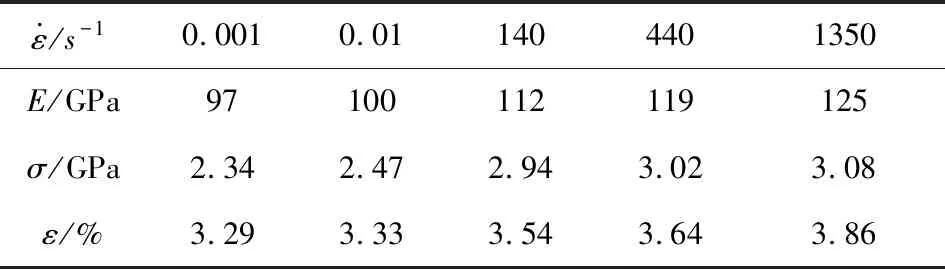
表1 Kevlar49纤维力学特性参数[34]Table 1 Mechanical properties of Kevlar49 fiber[34]

由表1数据结果得到Kevlar49纤维材料Johnson-Cook模型相关参数为：A=2729,B=60.79,C=0.0389,n=1,m=1[34]。

本文利用文献[35]中得到的Kevlar49纤维织物超高速碰撞实验结果,对所建立的纤维织物超高速碰撞热-力学单胞模型进行验证。该实验采用二级轻气炮展开超高速碰撞实验研究,得到了不同速度弹丸对不同厚度纤维织物的碰撞特性。实验中的纤维织物厚度为3.80 mm,7层；弹丸为Al2024T351材料,直径3.97 mm,初始速度为3.80 km/s。

基于纤维织物超高速碰撞热-力学单胞模型,建立了Kevlar49纤维织物与铝弹丸超高速碰撞模拟的数值模型,如图2所示。

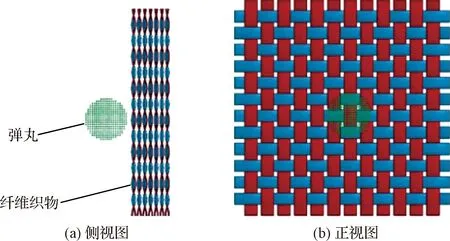
图2 纤维织物超高速碰撞数值模型Fig.2 Numerical model for hypervelocity impact of fiber fabric

2.1 碎片云特性分析

对Kevlar49纤维织物与铝弹丸超高速碰撞模拟及实验得到的结果进行了对比分析,图3给出了弹丸入射面穿孔形貌的对比。

图3 弹丸入射面穿孔形貌图Fig.3 Morphology of perforation on projectile’s incidence surface

从图3可以看出,弹丸入射面穿孔周围的纤维向内卷曲,形成一个近似圆形的穿孔,模拟得到的穿孔面积为13.12 mm2,实验结果为12.56 mm2,计算结果误差为4.4%,说明纤维织物热-力学单胞模型模拟结果与实验结果符合较好。

图4为模拟与实验结果得到的弹丸出射面穿孔形貌对比。

图4中,模拟和实验结果中出射面穿孔边缘纱线均沿弹丸速度方向外翻,这是纤维在碎片云冲击下变形的结果,模拟结果得到穿孔面积为29.32 mm2,实验结果为28.26 mm2,误差为3.75%,与实验所得结果符合较好。

图4 弹丸出射面穿孔形貌图Fig.4 Morphology of perforation on projectile’s surface

从上述结果还可以看出,弹丸出射面穿孔面积远大于入射面,这是由于弹丸破碎为碎片云后,以一定的扩散角穿过多层Kevlar49纤维织物,从而导致其穿孔的出射面尺寸显著大于入射面。

图5为模拟得到的不同时刻碰撞区域剖面应力分布的侧视图。

图5 不同时刻碰撞区域剖面应力分布(侧视图)Fig.5 Stress distribution of impact section zone with time(Side view)

从图5(a)可以看出,碰撞初期,在弹丸碰撞作用下,尚未与弹丸发生碰撞的纤维束已经产生较高的应力集中,这说明弹丸与纤维束、纤维束与纤维束之间发生接触、挤压等相互作用,这是单纯采用SPH模型无法得到的,这也说明了该模型采用FEM-SPH耦合算法在分析相互作用方面的优势。另外,弹丸与纤维织物超高速碰撞后,弹丸首先破碎为碎片云,随后,碎片云以一定的扩散角穿过多层Kevlar49纤维织物,这导致其穿孔的出射面尺寸显著大于入射面。

碰撞过程中弹丸及其所形成的碎片云的动能随时间变化曲线如图6所示。

图6 弹丸动能随时间变化曲线Fig.6 The kinetic energy of projectile with time

从图6可以看出,与纤维织物碰撞后,弹丸及碎片云动能迅速下降,在1.0 μs时基本降至最低,之后动能保持不变,说明弹丸在穿透7层纤维织物的过程中,其能量被纤维织物不断吸收,并在1 μs时完全穿过纤维织物。

2.2 温度场分析

纤维织物与铝弹丸的超高速碰撞过程中,碰撞区域不仅会发生变形、侵彻、破碎等现象,极高的冲击压力还会导致碰撞区域产生剧烈温升,这会导致纤维织物产生软化等热学效应,并影响其超高速碰撞特性及防护性能。图7为超高速碰撞不同时刻纤维织物碰撞区域剖面温度分布。

从图7可以看出,碰撞区域及其周围区域在碰撞过程中发生剧烈的温升,温度峰值为800 ℃,远高于kevlar49纤维分解温度(约500 ℃),这将会导致纤维的分解、碳化,这与实验中观察到的多层纤维织物碰撞区域的碳化现象一致,如图8所示。

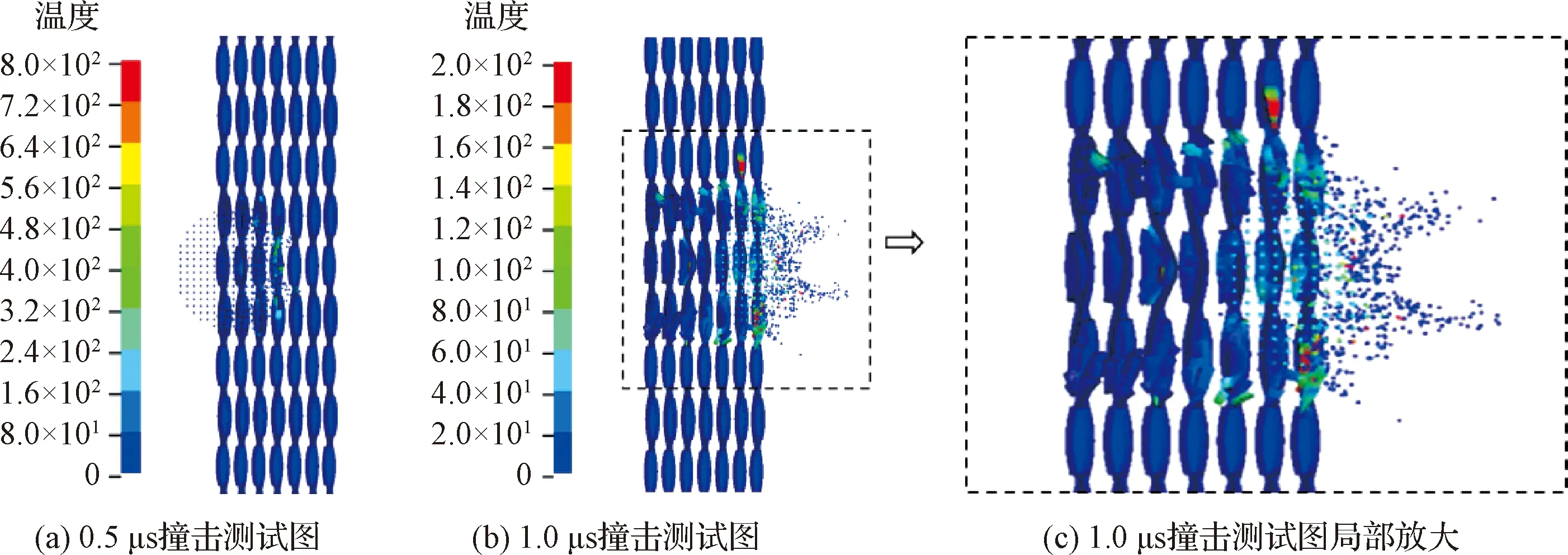
图7 温度云图Fig.7 Temperature cloud

图8 实验中纤维织物剖面图Fig.8 Profile of fiber fabric in the experiment

从图8可以看出,在弹丸穿孔周围的芳纶纤维发生碳化、颜色变黑,验证了计算结果的正确性,也说明了超高速碰撞过程中存在显著的热效应。

为进一步分析纤维织物碰撞过程中温度场分布规律,取A,B,C三个特征点,如图9所示,A点为碰撞区域的中心位置,A,B点处于碰撞区域内,C点处于碰撞区域外。各点温度随时间变化曲线图如图10所示。

图9 A,B,C点位置示意图Fig.9 Location diagram for point A,B,C

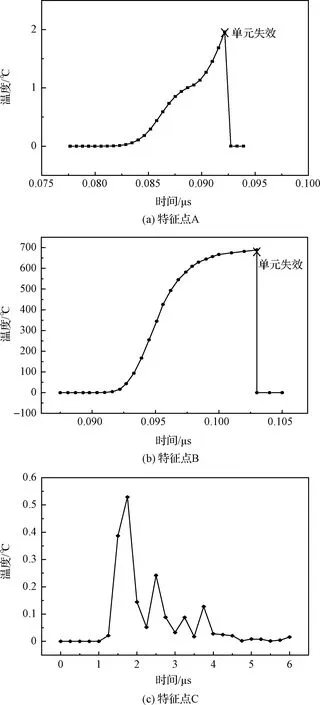
图10 A,B,C点温度变化曲线图Fig.10 Temperature points A,B,C

图10中,各点在极短时间内(6 μs)快速升温且降温,其中B点温度变化最为剧烈,在0.01 μs内温度由0 ℃升到最高温度约700 ℃,说明超高速碰撞所产生的热效应非常显著。曲线图中,由于碰撞区域中的A,B点在碰撞过程中失效,其温度变化也分别在0.093 μs和0.103 μs时中止。此外,碰撞区域外的C点也发生了升温,并分别在1.8 μs时达到峰值,这是碰撞区域产生热量的热传递所导致,但峰值温度很低,是传热时间短,而总的热量有限所致。

3 结 论

本文对纤维织物超高速碰撞热-力学数值模型进行了研究,分析了纤维织物超高速碰撞热-力学特性,得到如下结论：

1)引入Johnson-Cook模型及Gruneisen状态方程,考虑纤维织物的纱线编织结构,建立了纤维织物超高速碰撞热-力学单胞模型,该模型可计算得到纤维织物超高速碰撞过程中的侵彻、破碎、应力、应变等力学信息,及纤维织物的生热及温度场等热学信息,并可给出碰撞过程中纤维之间的相互作用信息。

2)对本文所建立的纤维织物超高速碰撞热-力学单胞模型计算结果进行了验证,其弹丸穿孔面积、断口形貌等计算结果与实验结果符合较好,其中,穿孔面积计算结果与实验结果误差在5%以内,验证了该模型的正确性。

3)模拟结果表明,纤维织物碰撞区域温度场分布与其位置密切相关,距离碰撞区域中心越远温度越低,其温度随时间变化越不明显。而在碰撞中心区域,其温度在极短时间内(约0.1 μs)快速升至峰值(800 ℃以上),这也很好的解释了实验中观察到的纤维碳化现象。

综上所述,本文建立的纤维织物超高速碰撞热-力学单胞模型,为纤维织物超高速碰撞热-力学特性分析提供了有效手段,可为纤维织物碎片防护结构设计提供更为详尽、全面的热-力学信息。