一种低轨星座高精度相位保持方法

刘 奇,向开恒,赵书阁,贺 泉,李小玉,张 楠

(1.航天科工空间工程发展有限公司,北京 100854；2.中国航天科工集团有限公司空间工程总体部,北京 100854)

0 引 言

近年来,利用大型低轨星座向全球提供宽带接入受到了广泛的关注[1],而星座构型稳定是星座发挥其正常功能的基础[2]。理论上,Walker星座中卫星之间的相对位置关系保持不变,但是由于卫星的入轨偏差及摄动力的不同,星座构型发散,从而影响星座的覆盖特性及任务实现,如何维持大型星座的构型稳定是大型星座在轨运行面临的一个关键问题[3]。

Walker星座构型保持的目标可以分解为以下三个方面：1)保持同轨道面卫星同间隔分布,同时还要保持与相邻轨道面的卫星之间的相对相位关系。2)保持轨道平面的等间隔性。3)保持星座整体的轨道高度与设计值的偏差不超过容许值。其中最重要的是第一方面,因为其对星座覆盖的影响最大,此外,通常也称其为相位保持[4]。

根据相位保持方法是控制每一颗卫星的绝对位置还是控制各卫星之间的相对位置,可以将相位保持分为绝对相位保持和相对相位保持。绝对相位保持为每一颗卫星规划相位时间历程,通过施加控制,使每一颗卫星的相位保持在其参考相位附近。相对相位保持的控制目标由每一颗卫星的绝对位置保持变为各卫星之间的相对位置保持,相对相位保持只修正星座内各卫星所受摄动的不同部分,对摄动的相同部分不予修正[4]。绝对相位保持的控制方法比较成熟可靠,有一定的工程应用基础,可以适用于任何星座[5]。此外,通过相位参考值的设置,绝对相位保持还可以同时实现轨道高度的维持。本文所提方法采用绝对相位保持。对于星座内的每一颗卫星,相位保持方法相同,仅参考相位不同,因此后续不针对星座展开描述,直接针对单颗卫星展开描述。

相位保持方法包括摄动补偿方法[5-6]、微分修正方法[7]和极限环保持方法[8]等,摄动补偿方法和微分修正方法的控制目标量都为终端时刻的状态量,并不包括整个时间历程内的状态量,仅适用于单边漂移的长期保持问题,相位保持精度超过1°[7],并不适用于相位保持范围为±0.1°的高精度相位保持问题。极限环保持方法通过调整半长轴,间接实现相位保持在一定范围内,适用于本文所研究的高精度相位保持问题,并且已经应用于静止轨道卫星的东西位置保持[8]。

根据本文第3章的数值仿真分析,对于某低轨卫星相位保持任务,为了实现平相位角偏差的瞬时轨道值(以下简称为“瞬轨值”)±0.1°的保持精度,平相位角偏差的平均轨道值(以下简称为“平轨值”)相对于参考值的变化范围应为±0.03°,极限环保持方法的单次半长轴改变量为28.7 m,因此,作为极限环保持方法的输入,半长轴平轨值的确定精度应尽量高。

对于半长轴平轨值,传统计算方法通常首先确定半长轴瞬轨值,然后采用瞬时轨道要素到平均轨道要素的转换获得。如果采用该计算方法确定高精度的半长轴平轨值,需要时长较长、采样间隔较短、精度较高的卫星定轨数据[9],这将给测控系统带来极大的压力。

由于平相位角随时间的变化趋势主要取决于半长轴,本论文利用这一特性提出了一种基于极限环的高精度相位保持方法。该方法根据实际平相位角与参考平相位角偏差随时间变化的零次项系数、一次项系数和二次项系数,直接反演计算实际半长轴与参考半长轴的偏差初始值和偏差一阶变化率,进而确定极限环控制的轨道机动时刻以及单次轨道机动半长轴改变量,用于实现低轨星座系统高精度相位保持。本方法对卫星的位置、速度确定精度要求不高,典型GNSS接收机的定轨精度即可满足要求；而且不需要对卫星位置、速度数据进行高频率采样,仅仅需要间隔一定时间(例如每隔一天)的位置、速度数据作为相位保持的输入即可,从而可以满足低轨大型星座自主相位保持需求。

1 数学模型

1.1 基于极限环的相位保持方法概述

低轨卫星在大气阻力的影响下,轨道高度产生变化导致卫星的相位相对于参考相位发生持续漂移,相位保持通过施加控制,使卫星的相位保持在其参考相位附近。本文的参考相位时间历程选取为卫星轨道半长轴、偏心率以及轨道倾角不变的条件下的相应值,参考相位对应的轨道称为参考轨道,卫星实际轨道要素与相应参考轨道要素的偏差定义为轨道要素偏差。

极限环保持方法的半长轴偏差与相位偏差的关系示意图如图1所示。由于大气阻力的作用,卫星半长轴减小,相位变化率逐渐增大,当卫星的相位偏差达到边界C时,通过轨道机动,增大卫星的半长轴,使卫星的半长轴偏差由C变为A、相位偏差变化率由正变为负,从而可以使卫星相位偏差从边界A向边界B变化,并且可以通过设置轨道机动的半长轴改变量,使卫星相位偏差达到边界B时的相位偏差变化率为零,之后卫星相位偏差从边界B向边界C变化,卫星的相位偏差变化率由零变为正,并在相位偏差达到边界C时,再次执行半长轴增大轨道机动,从而可以将相位偏差保持在Δλmin与Δλmax之间。

图1 极限环相位保持方法：半长轴偏差与相位偏差的关系示意图Fig.1 Phase keeping method based on limit cycle:The relationship between semimajor axis difference and phase angle difference

1.2 平均轨道要素

平均轨道要素在卫星星座设计中意义重大,使用合适的瞬时轨道要素与平均轨道要素间的转换公式,可以设计出构形更稳定的星座,减少相位维持所消耗的燃料[10]。同时,为了减小短周期项对轨道控制的影响,采用平均轨道要素作为相位保持轨道控制的输入[11]。本文提到的平均轨道要素指的是去除地球非球形带谐主项、田谐主项和大气阻力导致短周期项的拟平均轨道要素,其中的短周期项包括以(半)轨道周期和以(半)天为周期的周期项。

影响低轨卫星星座构形稳定性的主要摄动源包括地球非球形摄动和大气阻力摄动。地球非球形可分为带谐项和田谐项,带谐项与经度无关,主要带谐项J2,J3,J4是地球非球形引力位中对卫星影响最显著的部分[12],文献[13]给出了带谐主项导致的一阶短周期项公式。从地球非球形引力位的角度来看,带谐项是反映地球扁率效应的,而田谐项是反映地球赤道椭率效应的。文献[14]给出了田谐主项J22导致的短周期项公式。

考虑到单个相位保持周期约为十几到几十天,而田谐项主项J22导致的平相位角的短周期项的周期为0.5天,幅度约为0.0055°左右,所以在进行瞬时轨道要素到平均轨道要素转换时,相对于已有方法通常仅考虑地球带谐主项J2,J3,J4的影响,本文同时考虑了田谐主项J22的影响。

大气密度随高度增加而减小,其规律大致随高度呈指数递减。本文为了验证所提方法的可行性,采用一种简化的大气模型,美国标准大气模型(US 1976 Standard Atmospheric Density Model)。文献[9]给出了在该模型下大气阻力导致的卫星运动短周期项公式。

本文采用单点数据解析计算平均轨道要素,即基于瞬时轨道要素迭代计算短周期项,进而确定平均轨道要素。相对于递推方法或滤波方法[15],该方法的优点是在只有单个采样点定轨数据的情况下,可以直接确定该时刻的平均轨道要素,适用于定轨数据采样间隔较大的轨道控制问题。

表1和图2对比了分别去除带谐主项、田谐主项和大气阻力导致的短周期项后相位角偏差平轨值的波动情况,以分析不同摄动因素的影响大小。瞬轨值σo与去除带谐主项导致的短周期项的平轨值σm1的偏差振幅约为5.5×10-2(°),去除带谐主项导致的短周期项的平轨值σm1与去除带谐主项和田谐主项导致的短周期项的平轨值σm2的偏差振幅约5.5×10-3(°),去除带谐主项和田谐主项导致的短周期项的平轨值σm2与去除带谐主项、田谐主项和标准大气阻力导致的短周期项的平轨值σm3的偏差振幅约为7.9×10-8(°)。带谐主项导致平相位角偏差振荡幅度最大,田谐主项导致的振荡幅度比带谐主项导致的振荡幅度低1个量级,大气阻力导致的振荡幅度比田谐主项导致的振荡幅度低5个量级。图2还表明带谐主项和田谐主项导致平相位角偏差振荡周期分别为0.5个轨道周期和0.5天。

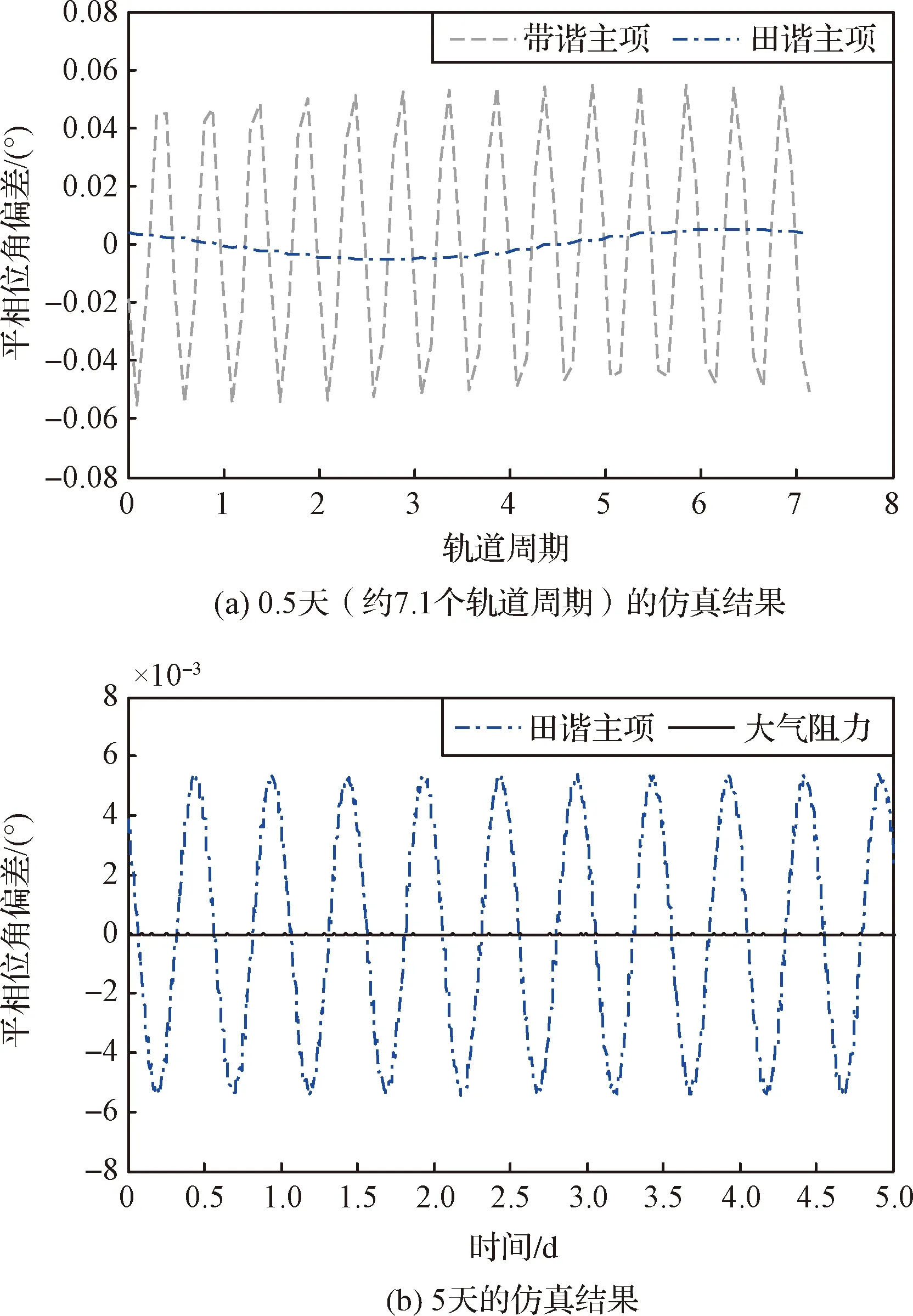
图2 相位角偏差短周期项时间历程Fig.2 Time history of short-periodic terms of phase angle difference

对于本文研究的近圆轨道,大气阻力导致的平相位角短周期项振幅远小于相位保持范围,在进行瞬时轨道要素到平均轨道要素转换时,可以不考虑大气阻力的影响,为了结果的完整性以及后续应用拓展,本文考虑了大气阻力导致的短周期项。

2 相位保持方法

2.1 半长轴偏差与相位偏差的关系

将卫星的近地点幅角ω与平近点角M之和定义为卫星的平相位角λ,本节建立平相位角偏差Δλ随时间变化的一次项系数、二次项系数与半长轴偏差初始值、半长轴偏差一阶变化率的关系。

在考虑地球中心引力场、地球非球形J2项以及大气阻力的情况下,平相位角变化率的解析表达式为[13]

(1)

为了在进行相位保持的过程中,同时实现轨道高度的维持,参考平相位角取为轨道半长轴、偏心率和轨道倾角均为常值对应的平相位角,从而参考平相位角变化率的解析表达式为

(2)

式中：下标c为参考轨道的相应轨道要素。式(1)与式(2)均为三项分量之和,接下来通过一个数值算例对比式(1)的三项分量与式(2)的三项分量之差的量级。表2给出用于平相位角变化率各分量量级对比的实际轨道和参考轨道的轨道要素,表3给出了实际平相位角变化率的各分量与参考平相位角变化率的相应分量的偏差。结果表明：后两项分量偏差的绝对值之和与第一项分量绝对值偏差之比为O(10-3),因此,式(1)与式(2)作差,后两项分量的差可以省略,平相位角偏差Δλ的一阶时间导数近似如下：

表3 平相位角变化率偏差Table 3 Mean phase angle change rate difference

(3)

式中:n的一阶时间导数为

(4)

由于相位保持过程中,实际半长轴接近参考半长轴,并且半长轴的一阶变化率主要由大气阻力导致,所以上式可以近似为

(5)

(6)

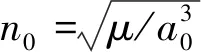
(7)

式中:Δλ0为初始时刻的平相位角偏差。

令

Δλ1=n0-nc

(8)

(9)

可以看出：Δλ0、Δλ1和Δλ2分别是平相位角偏差随时间变化的零次项系数、一次项系数和二次项系数。则式(7)可改写为

Δλ=Δλ0+Δλ1(t-t0)+Δλ2(t-t0)2

(10)

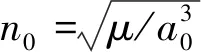
(11)

将上式代入式(8)可得

(12)

式中:Δa0=(a0-ac),为实际半长轴的初始值与参考半长轴的偏差,故Δa0可以由系数Δλ1确定。

(13)

(14)

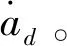
2.2 极限环的周期以及半长轴改变量

由于卫星从控制极限环的边界B(对应的平相位角差为Δλmin)自由漂移到边界C(对应的平相位角偏差为Δλmax)的时间为半个相位保持周期(ΔT/2),并且卫星处于边界B时,实际半长轴等于参考半长轴。以卫星处于边界B为初始时刻,卫星处于边界C为终端时刻,从而此场景下,由于初始时刻实际半长轴等于参考半长轴,从而Δλ1=0,因此,可以获得

(15)

则相位保持的周期为

(16)

所以,在一个相位保持周期,半长轴的衰减量为

(17)

从而,相位保持轨道机动的半长轴偏差目标值为

(18)

在卫星达到边界C时,卫星轨道机动的半长轴改变量为

δa=ΔaT-Δaf

(19)

式中:Δaf是卫星达到边界C时实际半长轴偏差,

(20)

式中:tf是卫星到达边界C的时刻。

对于近圆轨道,半长轴改变量δa所需切向速度增量为[16]

(21)

2.3 相位保持实施方法

本节基于以上两节获得的半长轴偏差与相位偏差的关系以及极限环的周期、半长轴改变量确定方法,给出一种相位保持实施方法。

不妨假设任务开始时刻,卫星的平相位角已经调整到保持区间内,将整个任务的开始时刻作为第一个相位保持周期的初始时刻,由于每一个相位保持周期的实施方法相同,重复采用一个相位保持周期的保持方法,即可实现整个任务周期的相位保持。接下来给出一个相位保持周期的相位保持实施方法,对应的实施框图如图3所示。

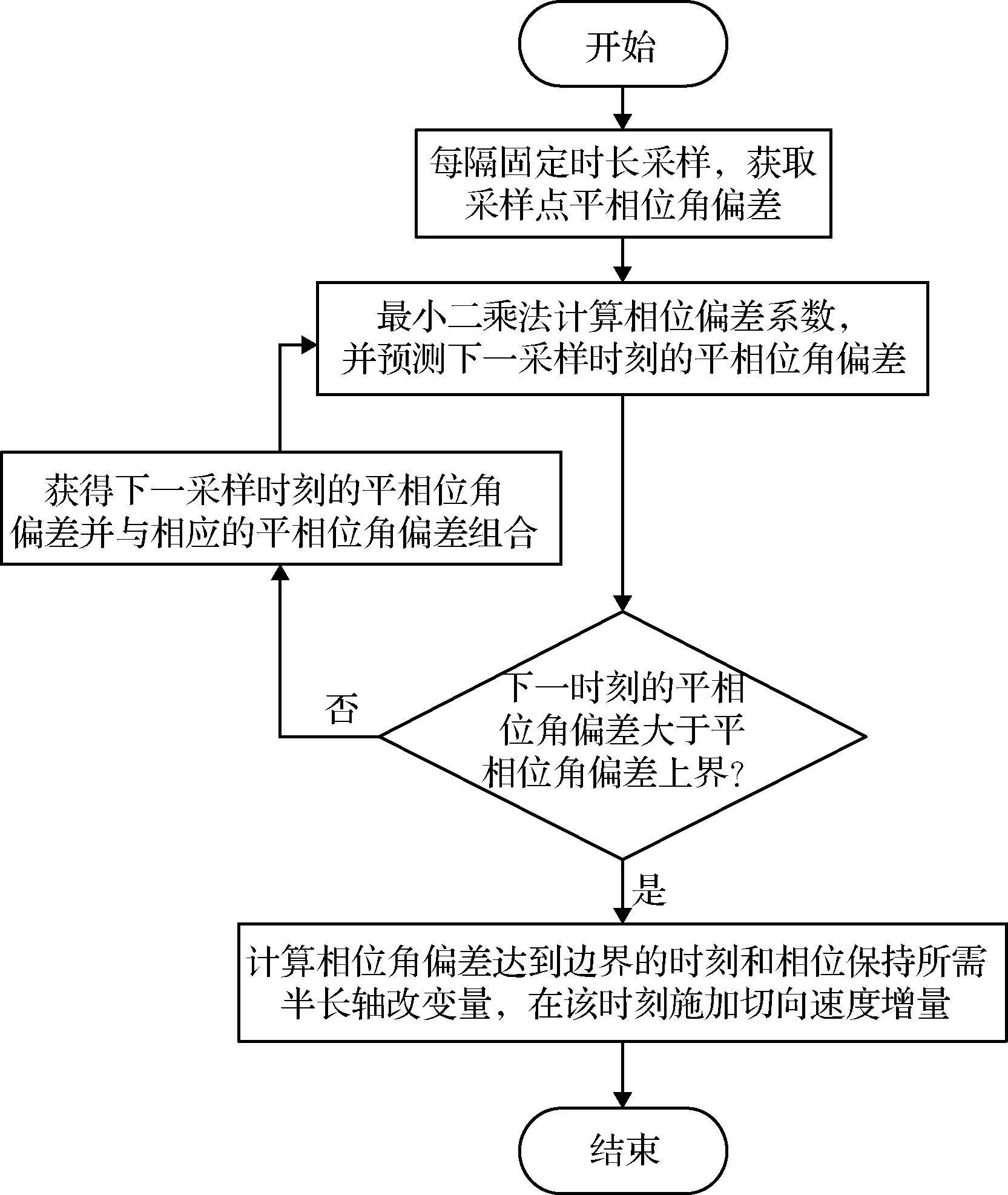
图3 相位保持实施框图Fig.3 Flow chart of phase keeping implementation

1)从初始时刻开始,每隔一定时长采样一次卫星的位置和速度数据,采用1.2节的方法,将其转化为平相位角的平轨值,并将其与相应时刻的参考平相位角作差,获得已采样时刻的平相位角偏差,转到步骤2)。

2)基于采样时刻的平相位角偏差数据,使用最小二乘法计算系数Δλ0、Δλ1和Δλ2。并基于计算获得的系数Δλ0、Δλ1和Δλ2,预测下一采样时刻的平相位角偏差Δλnext,转到步骤3)。

3)如果Δλnext<Δλmax,在当前采样时刻至下一采样时刻不施加相位保持轨道机动,转到步骤4)；如果Δλnext≥Δλmax,则在当前采样时刻至下一采样时刻期间施加相位保持轨道机动,转到步骤5)。

4)获得下一采样时刻的平相位角偏差采样数据后,与已有的平相位角偏差数据组合,转到步骤2)。

3 仿真校验与分析

3.1 仿真校验条件设置

本节通过实际的相位保持任务验证本文提出方法的有效性,仿真算例的卫星参考轨道高度取为800 km,初始轨道要素见表4。卫星的初始质量取为200 kg,太阳帆板面积取为3.5 m2,相位保持任务周期取为180天,定轨数据采样间隔取为1天,三轴位置确定误差取为10 m(1σ),三轴速度确定误差取为0.1 m/s(1σ)。

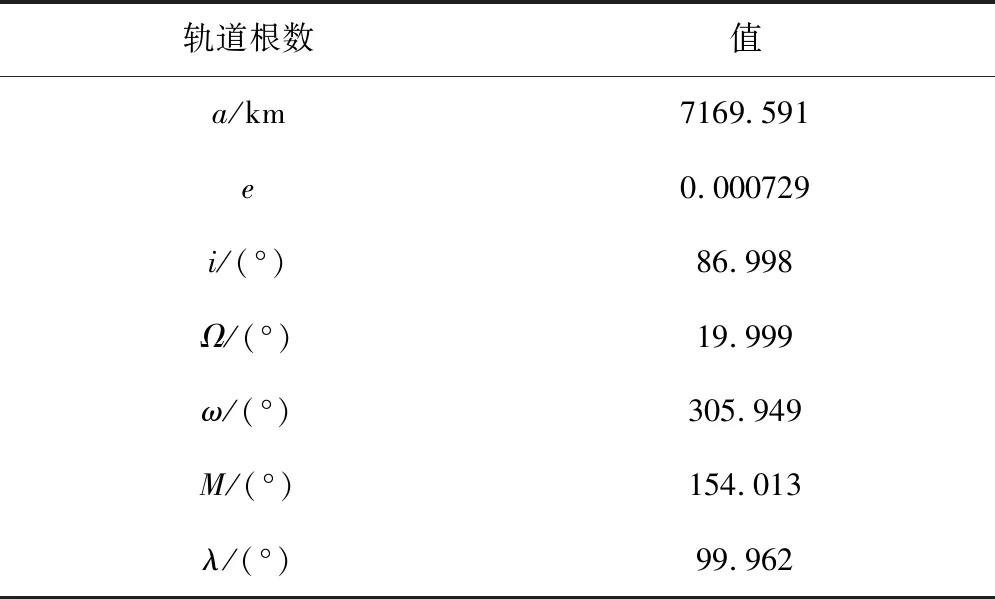
表4初始瞬时轨道根数Table 4 Initial osculating orbit elements

假设任务要求将平相位角偏差的瞬轨值保持在±0.1°的区间内,根据文献[13]的地球带谐主项导致的短周期项公式,由地球带谐主项导致的平相位角偏差瞬轨值振幅约为0.055°；根据文献[14]的地球田谐主项导致的短周期项公式,由地球田谐主项导致的平相位角偏差瞬轨值振幅约为0.0055°；根据文献[9]的大气阻力主项导致的的短周期项公式,由大气阻力导致的平相位角偏差瞬轨值振幅约为7.9×10-8(°),综合瞬平转换中未考虑到的高阶短周期项,且保留一定控制裕度,将平相位角偏差的平轨值保持在区间[-0.03°,0.03°]内,即Δλmin=-0.03°,Δλmax=0.03°。

在半长轴随大气阻力严格一阶线性变化的理想条件下,采用解析方法,根据式(16)计算获得的单个极限环保持周期为14.87天,根据式(17)计算获得的极限环单次控制半长轴改变量为30.06 m。

数值仿真的主要目的是验证所提方法的有效性,因此在建模中只考虑了对低轨卫星影响最大的地球非球形和大气阻力摄动。地球非球形摄动采用WGS84-EGM96模型,Degree和Order设为4,大气阻力摄动采用US 1976 Standard Atmospheric Density Model。仿真开始时间为1st Jan 2020 00:00:00.000 UTCG。

3.2 仿真结果与分析

采用本文提出的相位保持方法进行数值仿真,相位保持全任务周期和某一相位保持周期的平相位角偏差时间历程如图4所示,图中点划线、虚线、实线、点线分别代表瞬轨值、仅去除带谐主项导致的短周期项的平轨值、进一步去除田谐主项导致的短周期项的平轨值、进一步去除大气阻力导致的短周期项的平轨值。图中实线和点线基本重合,是因为由大气阻力导致的振荡幅度太小,比田谐主项导致的振荡幅度低5个量级。从图(a)的全任务周期的仿真结果可以看出平相位角瞬轨值偏差控制在±0.1°以内,平相位角平轨值偏差基本上保持在±0.03°以内,本文所提方法实现了预期的高精度相位保持,仿真结果验证了本文所提方法的有效性。从图(b)的某一相位保持周期的仿真结果可以看出：在去除带谐项导致的短周期项的基础上,再去除田谐项导致的短周期项,可以进一步去除田谐项导致的轨道周期为0.5天的振荡项,证明了本相位保持方法在进行瞬平轨道转换时,去除田谐项导致的短周期项的作用。

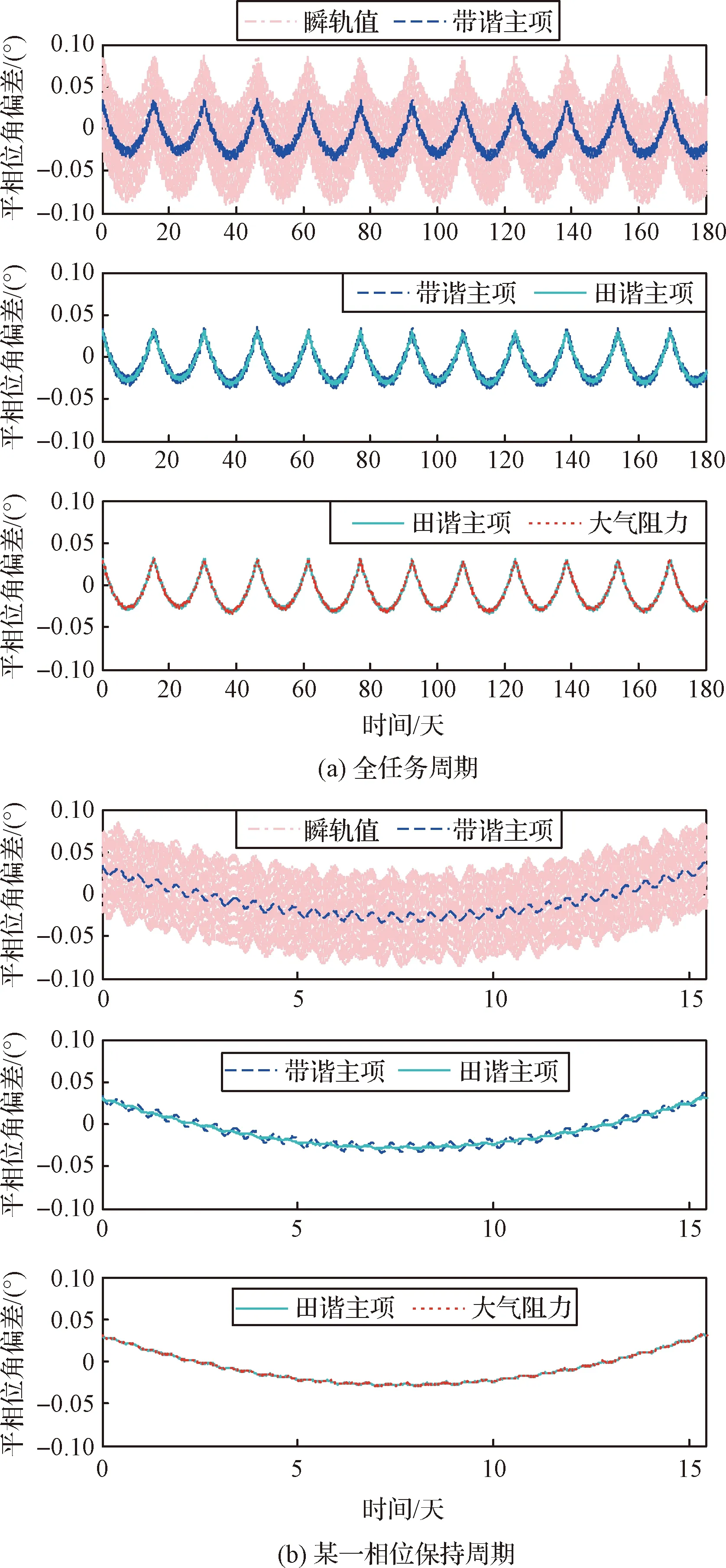
图4 平相位角偏差时间历程Fig.4 Time history of mean phase angle difference

轨道机动时刻以及半长轴改变量的统计结果见表5,从表中可以看出单个相位保持周期的时长平均值为15.40天,单次轨道机动半长轴改变量平均值为28.70 m,分别与上一节获得的半长轴随大气阻力严格线性变化的理想条件下的保持周期时长、单次轨道机动半长轴改变量相对偏差都在5%以内。

表5 轨道机动时刻以及半长轴改变量Table 5 Orbital maneuver epoch and semimajor axis change

半长轴平轨值偏差时间历程如图5所示,图中信息表明,即使在瞬平转换之中去掉了由带谐主项、田谐主项和大气阻力导致的短周期项,半长轴平轨值偏差仍然存在百米级的振荡,相应绝对值的平均值为34.42 m。因此,利用瞬时轨道要素单点值直接计算短周期项,进而确定相应时刻的半长轴平轨值,无法满足高精度相位保持的需要。虽然采用递推法或滤波方法可以大幅度提高半长轴平轨值的确定精度[9],但这类方法需要采用间隔较短、时长较长的观测数据,对于星座规模较大的低轨星座,这将极大增加测控系统的运行成本和复杂度。

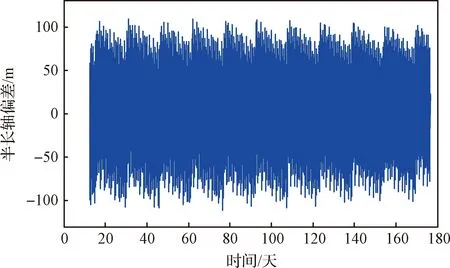
图5 半长轴平轨值偏差时间历程Fig.5 Time history of mean semimajor axis difference

因此,本文所提方法通过平相位角偏差反演半长轴偏差变化率和偏差初值,在卫星定轨精度不高、采样间隔时间较长的情况下,能实现星座系统的高精度相位保持,具有很大优势。

4 结 论

本文提出了基于极限环的高精度相位保持方法,该方法创新性地建立了平相位角偏差与平半长轴偏差的关系,并利用平相位角偏差随时间变化的趋势,直接反演计算实际半长轴与参考半长轴的偏差,进而确定相位保持半长轴改变量,用于实现低轨星座系统高精度相位保持。本文提出的方法可以在卫星定轨精度不高、采样间隔较大的情况下实现卫星高精度相位保持,避免了半长轴平轨值直接确定精度较低带来的相位保持效果较差的问题,具有较大的工程应用价值。

本文提出的相位保持方法虽然是针对单颗卫星展开描述的,但对于大规模低轨星座系统,在每颗卫星选取相应参考相位的情况下,可以用于实现低轨星座系统的高精度相位保持。