掘进机姿态参数测量及解算方法

郭伦锋， 郭一楠,2， 蒋康庆， 葛世荣,2

(1.中国矿业大学(北京) 机电与信息工程学院， 北京 100083；2.中国矿业大学(北京) 智慧矿山与机器人研究院， 北京 100083)

0 引言

掘进机高精度姿态参数测量是实现其自主导航和定向截割的基础。现有掘进机姿态参数测量方法主要有基于激光靶[1-3]、基于视觉测量[4-6]、基于多点测量[7-9]和基于航位推算的方法[10]。基于激光靶的方法一般只能获得部分位姿参数，若要获得全部位姿参数，会导致测量系统复杂性较高，成熟度不足。基于视觉测量的方法解算较复杂，且易受环境干扰而失效。基于多点测量的方法一般需要先计算出机身多个点的坐标，再据此计算机身的姿态，因此姿态角测量误差较大，且测量实时性较差。基于航位推算的方法存在累积误差，且惯导的价格较为昂贵。

双轴倾角仪具有产品成熟、价格便宜、解算简单、测量频率高、不易受外界环境干扰等优点，可以实现较可靠的角度测量。然而，不少掘进机位姿测量研究中对双轴倾角仪的使用存在误区，即将双轴倾角仪输出的倾角直接作为掘进机的俯仰角和横滚角。实际上，掘进机的俯仰角和横滚角分别通过机身坐标系Y轴和X轴向巷道坐标系平面投影的方式定义[11]，因此，必须同时确定机身坐标系Y轴和X轴在巷道坐标系中的方向，才能同时得到掘进机的俯仰角和横滚角。根据双矢定姿原理[12]，必须首先得到掘进机机身坐标系与巷道坐标系的姿态转换矩阵，才能解算出俯仰角和横滚角。而通过双轴倾角仪可以解算的倾角是两轴相对于大地参考水平面、通过欧拉角定义的俯仰角和翻滚角[13]。

在水平巷道中，仅使用双轴倾角仪无法得到航向信息，从而无法确定掘进机机身坐标系和巷道坐标系的姿态转换矩阵，所以不能解算出掘进机的俯仰角和横滚角。在倾斜巷道中，尽管巷道倾角已知，但是由于缺少航向信息，不能将双轴倾角仪相对于水平面的参数转换到巷道坐标系，同样不能解算出掘进机的俯仰角和横滚角。因此，不论是在水平巷道还是倾斜巷道中，单独使用双轴倾角仪均无法进行俯仰角和横滚角测量，需将双轴倾角仪与能获取掘进机航向信息的定位方法进行融合，才能同时解算出掘进机全姿态参数。

本文首先介绍了掘进机姿态参数测量及双轴倾角仪测量的原理，以此为基础，针对水平巷道和倾斜巷道2种情况，对融合扇形激光与双轴倾角仪、融合机身两点坐标与双轴倾角仪2种掘进机姿态解算方法进行了推导和验证。

1 掘进机姿态参数测量及双轴倾角仪测量原理

1.1 掘进机姿态参数测量原理

掘进机姿态参数测量坐标系如图1所示。设巷道坐标系为{h}，其中Yh轴与巷道设计中轴线方向一致，Zh轴垂直于巷道底板。设机身坐标系为{b}，其中Xb轴为机身横轴，Yb轴为机身中线。设安装在掘进机上的双轴倾角仪的坐标系为{q}，假设不考虑双轴倾角仪的角度安装误差，则双轴倾角仪坐标系与掘进机机身坐标系对应轴方向一致。在实际掘进过程中，由于许多巷道具有一定坡度，所以还需要解析双轴倾角仪与巷道水平坐标系{d}之间的关系。巷道水平坐标系原点Od与巷道坐标系原点Oh重合，Xd轴与Xh轴重合，Zd轴与该坐标系原点处的水平面垂直，Yh轴与Yd轴的夹角为θ，即倾斜巷道的坡度。

图1 掘进机姿态参数测量坐标系Fig.1 Coordinate system of attitude parameter measurement for roadheader

掘进机位姿解算就是通过机身坐标系与巷道坐标系的相对位姿变换关系，获得掘进机相对于巷道坐标系的三维坐标(x,y,z)、偏航角α、俯仰角β和横滚角γ。将机身坐标系平移到巷道坐标系原点，如图2所示。偏航角α为Yb轴在巷道坐标系XhOhYh上的投影与Yh轴的夹角；俯仰角β为Yb轴在YhOhZh上的投影与Yh轴的夹角；横滚角γ为Xb轴在XhOhZh上的投影与Xh轴的夹角。

图2 掘进机姿态参数Fig.2 Roadheader attitude parameters

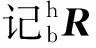
(1)

(2)

1.2 双轴倾角仪测量原理

双轴倾角仪通过检测重力方向来测量Xq轴和Yq轴与水平面的夹角ωr和ωp，如图3(a)所示。考虑到移动设备的航向角α′、俯仰角β′和翻滚角γ′采用Z-X-Y(旋转轴顺序)方式的欧拉角定义[14]，根据双轴倾角仪坐标系{q}和欧拉角的定义，基于O点建立与测量参考坐标系方向一致的坐标系{1}；随后，将该坐标系绕Z1轴旋转α′后形成坐标系{2}，如图3(b)所示；再将坐标系{2}绕X2轴旋转β′后，形成坐标系{3}，如图3(c)所示；最后，将坐标系{3}绕Y3轴旋转γ′，形成坐标系{q}，如图3(d)所示。对比图2中的α、β和γ与图3中的α′、β′和γ′可知，即使在水平巷道中，β与β′、γ与γ′均不相等，进一步说明了不能仅通过双轴倾角仪解算掘进机俯仰角和横滚角。

(a) 倾角仪测量参数

(b) 坐标系{1}绕Z1轴旋转α′

(c) 坐标系{2}绕X2轴旋转β′

(d) 坐标系{3}绕Y3轴旋转γ′图3 双轴倾角仪测量参数转换Fig.3 Conversion of measurement parameters of biaxial inclinometer

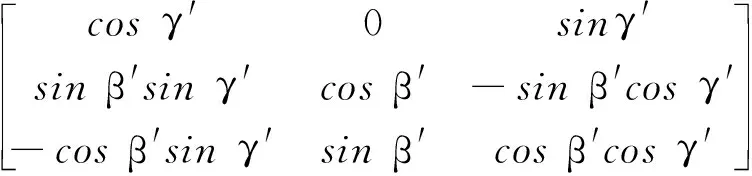
(3)

sinγ′=sinωr/cosβ′

(4)

基于此，通过双轴倾角仪可以解算出移动设备与水平面间通过欧拉角方式表达的俯仰角β′和翻滚角γ′。

2 水平巷道中掘进机姿态解算方法

水平巷道掘进时，巷道坐标系的XhOhYh面在水平面上，如图4所示。当采用不同偏航角测量方法时，其对应的俯仰角β和横滚角γ的解算方式存在差异。

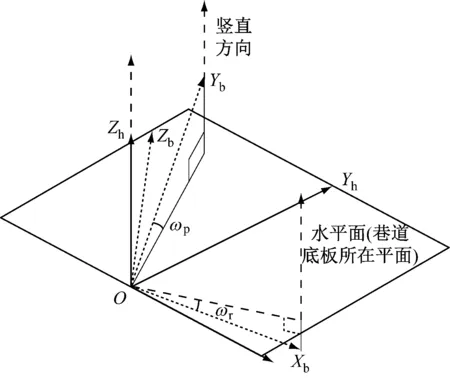
图4 水平巷道中机身坐标系与竖直方向的关系Fig.4 Relationship between roadheader body coordinate system and vertical direction in horizontal roadway

2.1 融合扇形激光和双轴倾角仪的姿态解算方法

将扇面激光发射器安装在巷道后方的顶板上，形成扇形激光束；通过平行安装在掘进机机身上方的2个激光标靶所获得的扇形激光束光斑位置，可实时确定掘进机相对于巷道坐标系的偏航角α[1]。

对比底板水平时掘进机偏航角α与欧拉角中航向角α′的定义可知，两者数值相等，即α=α′。通过双轴倾角仪可以获得掘进机机身相对于巷道坐标系的俯仰角β′和翻滚角γ′，则坐标系{b}与坐标系{h}的姿态转换矩阵为

(5)

基于式(1)和式(2)，可求得掘进机的偏航角α、俯仰角β和横滚角γ：

(6)

2.2 融合机身两点坐标和双轴倾角仪的姿态解算方法

当采用全站仪[15]、UWB(Ultra Wide Band，超宽带)[7]、iGPS(indoor GPS，室内全球定位系统)[16]与双轴倾角仪融合进行姿态解算时，先测量掘进机机身上2个待测点在巷道坐标系下的三维坐标，记为(X1h,Y1h,Z1h)，(X2h,Y2h,Z2h)，然后利用双矢定姿原理[12]确定掘进机姿态。2个待测点相对于机身坐标系的三维坐标(X1b,Y1b,Z1b)，(X2b,Y2b,Z2b)可通过标定获得。基于2个待测点的连线方向构造矢量v1，求得v1在机身坐标系和巷道坐标系下的表达v1b,v1h：

(7)

(8)

(9)

在水平巷道中，巷道坐标系{h}的Zh轴正方向竖直向上。因此，竖直向上的单位矢量v2在巷道坐标系中的表达为

(10)

设用双轴倾角仪获得的Xb轴和Yb轴与水平面的夹角分别为ωr与ωp，则两轴与水平面的法向量的夹角分别为ωr+π/2和π/2-ωp，v2在Xb轴和Yb轴上的投影分别为-sinωr与sinωp。单位矢量的模为1，则单位矢量v2在掘进机机身坐标系中的表达为[17]

(11)

(12)

(13)

当v1与v2不共线时，联立式(9)、式(12)和式(13)构造矩阵方程：

(14)

(15)

综合上述过程，结合式(1)、式(2)即可得到掘进机的姿态参数α,β和γ。

3 倾斜巷道中掘进机姿态解算方法

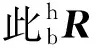
(16)

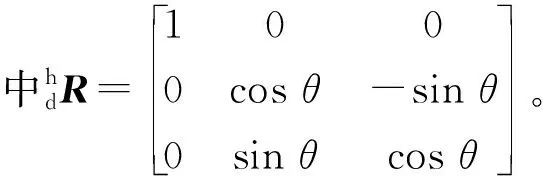
图5 倾斜巷道中机身坐标系与竖直方向的关系Fig.5 Relationship between roadheader body coordinate system and vertical direction in inclined roadway

在倾斜巷道中，通过扇形激光可直接测得掘进机相对巷道坐标系的偏航角α，则Yb轴在巷道底板上的投影与Yh轴之间的夹角为α。在掘进机机身坐标系的Yb轴上找一点A(图5)，使OA=1，则矢量OA在机身坐标系的映射v1b为

(17)

通过A点分别作巷道底面和巷道水平投影面的垂线，与2个面分别交于C点和B点。连接线段OC与OB，则∠AOB=β″，且|AB|=sinβ″。通过C点作Yh轴的垂线CD，由掘进机偏航角α的定义可知∠COD=α。设∠AOC=β，则|AC|=sinβ，|OC|=cosβ，|CD|=|OC|sinα=cosβsinα，|OD|=|OC|cosα=cosβcosα。OA在巷道坐标系的映射为

(18)

因为式(18)中的sinβ和cosβ未知，所以需求解这2个量。将v1h变换到巷道水平坐标系，得到OA在巷道水平坐标系的映射：

(19)

由式(19)可得|AB|=sinθcosβcosα+cosθsinβ，由前面分析可知|AB|=sinβ″，联立两式得

sinβ″=sinθcosβcosα+cosθsinβ

(20)

根据sin2β+cos2β=1，结合式(20)，可求出掘进机上坡工况下，即θ∈[0°,20°]，α∈[-45°,45°]，β∈[-20°,20°]，γ∈[-20°,20°]时，满足如下关系：

(21)

(22)

掘进机在下坡工况下，即θ∈[-20°,0°]，α∈[-45°,45°]，β∈[-20°,20°]，γ∈[-20°,20°]时，cosβ与上坡工况下一致，sinβ满足如下关系：

(23)

将式(21)—式(23)代入式(18)可得到v1h。竖直方向的单位矢量v2在巷道水平坐标系的映射为

(24)

对矢量v2d进行转换，得到OA在巷道坐标系的映射：

(25)

4 仿真分析

4.1 仿真模型搭建

为了验证本文给出的掘进机位姿解算方法的正确性，采用Gazebo搭建仿真环境[18]，构建水平巷道和倾斜巷道，如图6所示。通过在底板放置木板来模拟巷道中的起伏地形，控制差速小车在模拟巷道中运行，模拟掘进机在巷道中的行驶过程。在模拟过程中，采用Gazebo发布的小车机身翻滚角和俯仰角作为双轴倾角仪的测量值。验证水平巷道中融合扇形激光和双轴倾角仪的姿态解算方法时，采用Gazebo发布的小车机身偏航角作为扇形激光的测量值。在倾斜巷道中，需将发布的偏航角转换到巷道坐标系。为了方便描述，将融合扇形激光和双轴倾角仪的姿态解算方法记为方法1，将融合机身两点坐标和双轴倾角仪的姿态解算方法记为方法2，将把双轴倾角仪输出参数直接作为掘进机俯仰角和横滚角的方法记为原方法。

(a) 水平巷道

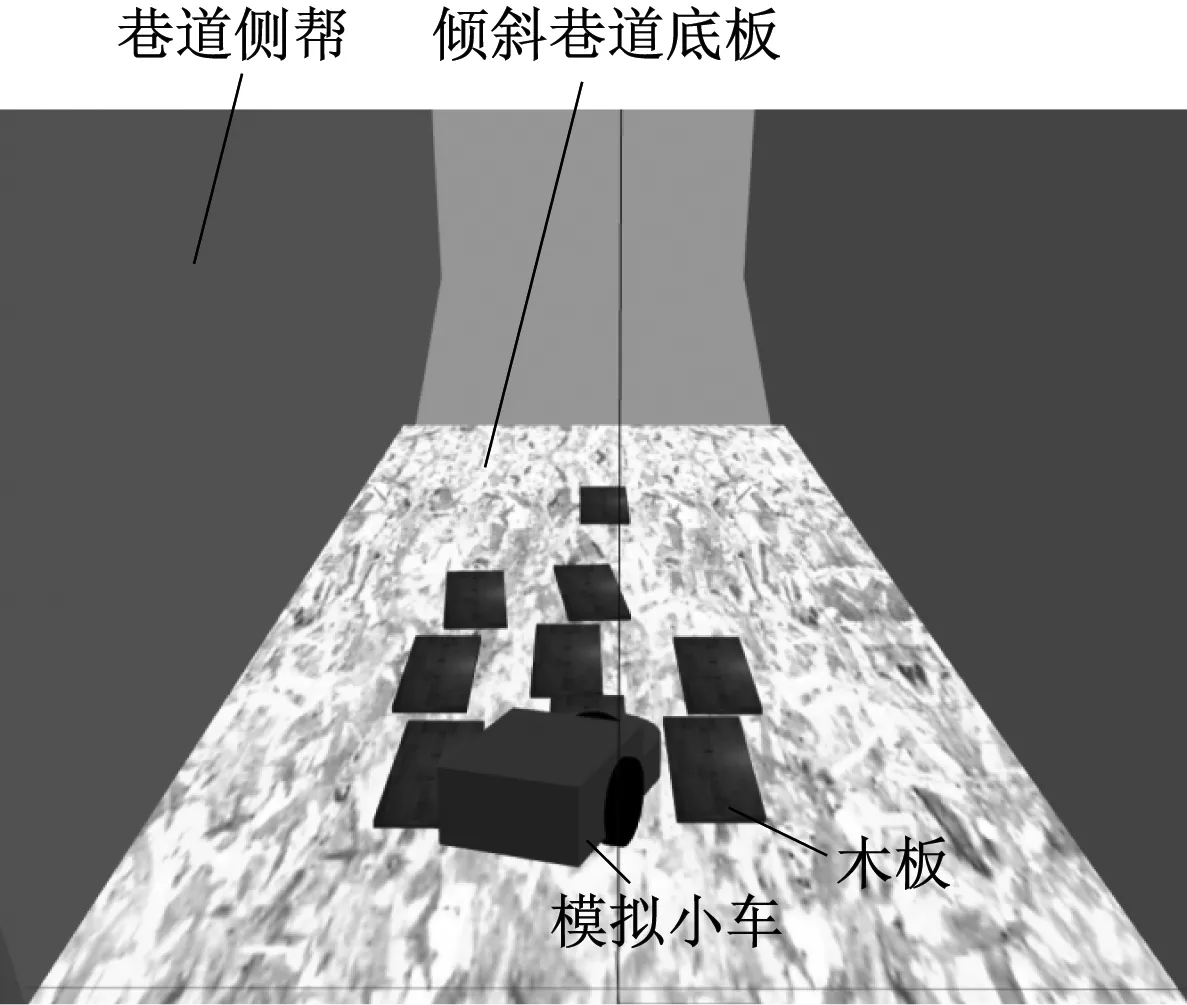
(b) 倾斜巷道图6 模拟水平巷道和倾斜巷道Fig.6 Simulation of horizontal roadway and inclined roadway

选取掘进机机身上同一高度的4个参考点A′(xA′,yA′,zA′),B′(xB′,yB′,zB′),C′(xC′,yC′,zC′),D′(xD′,yD′,zD′)，以D′A′和B′C′分别作为机身纵向的Yb轴和横向的Xb轴，如图7所示。采用rosbag命令行工具对各点坐标与机身参数进行录制，并将得到的bag文件导入Matlab进行姿态解算。

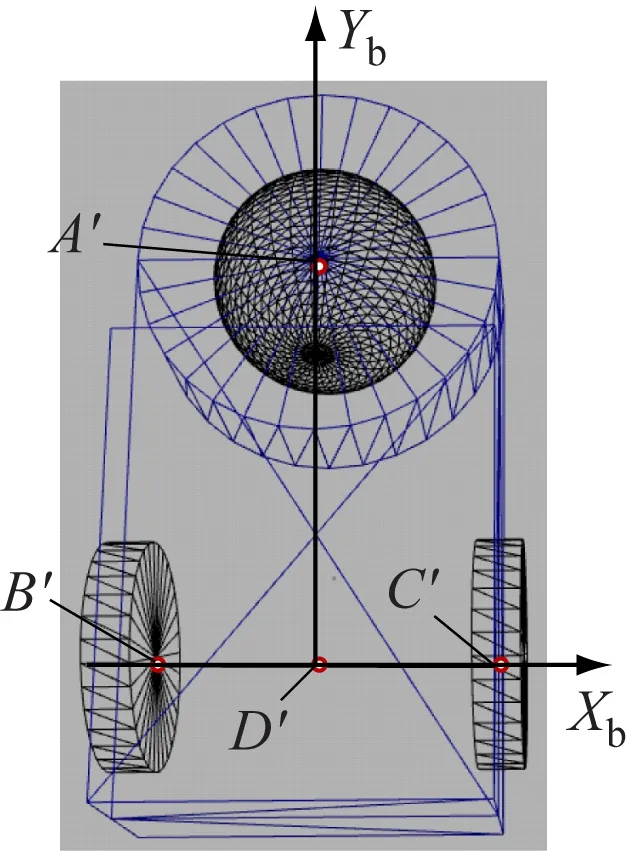
图7 掘进机机身上的4个参考点Fig.7 Four reference points on roadheader

4.2 水平巷道中解算方法验证

验证水平巷道中的2种解算方法时，根据掘进机姿态参数定义方法，得到其偏航角、俯仰角和横滚角的参考真值αc,βc和γc。

(26)

将基于小车机身各点坐标与角度信息解算获得的姿态参数与参考真值进行比较，2种方法的测量误差曲线分别如图8和图9所示。解算值与参考真值误差的均值E和标准差δ见表1。

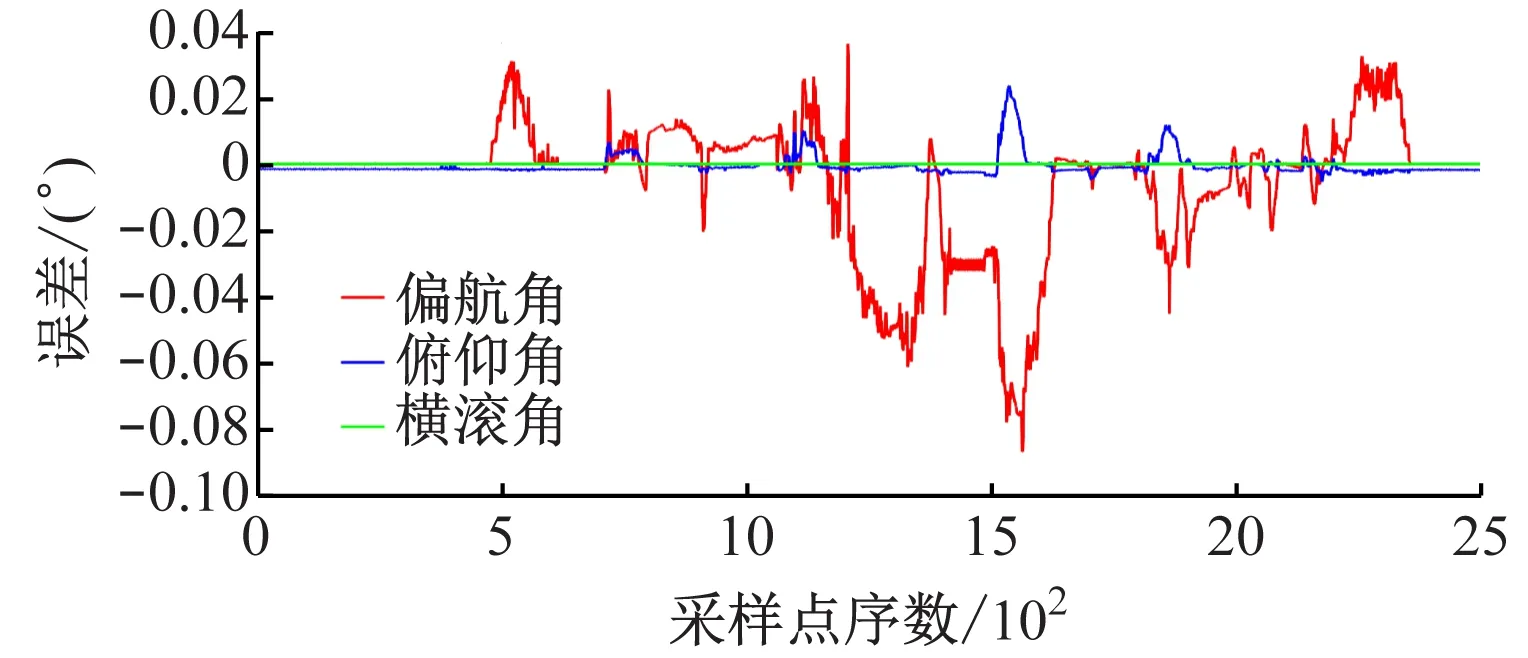
图8 水平巷道中方法1姿态参数测量误差Fig.8 Attitude measurement error of method 1 in horizontal roadway

图9 水平巷道中方法2姿态参数测量误差Fig.9 Attitude measurement error of method 2 in horizontal roadway

表1 水平巷道姿态参数误差均值与标准差Table 1 mean value and standard deviation of attitude parameter error of horizontal roadway (°)

仿真分析结果表明，原方法的角度误差较大，而方法1和方法2解算误差均很小，最大角度误差均值为0.004 9°，说明在水平巷道中，这2种掘进机姿态解算方法是合理的。

4.3 倾斜巷道中解算方法验证

验证倾斜巷道中的2种解算方法时，将4个参考点A′,B′,C′,D′在世界坐标系下的坐标转换到巷道坐标系下，再根据掘进机姿态参数定义方法，得到偏航角、俯仰角和横滚角的参考真值：

(27)

设巷道倾角为-15，-10，10，15°，利用各倾角下测得的机身坐标与角度信息，采用2种方法进行姿态解算。将解算出的姿态参数与参考真值进行比较，得到测量误差曲线，如图10所示。解算值与参考真值误差的均值E和标准差δ见表2。

由图10和表2可见，在4种不同倾角的巷道中，原方法的误差较大，难以满足掘进机姿态参数测量需要；方法1和方法2的误差都很小，最大角度误差均值为0.025°，验证了在倾斜巷道中2种掘进机姿态解算方法的合理性。此外，图10中的误差曲线在中间段的波动是由于Gazebo本身存在一定的模型误差，且在运行中段小车方向发生较大改变时造成了误差的叠加。

图10 不同倾角巷道中2种方法的姿态参数测量误差Fig.10 Attitude measurement errors of two methods in roadways with different inclination angles

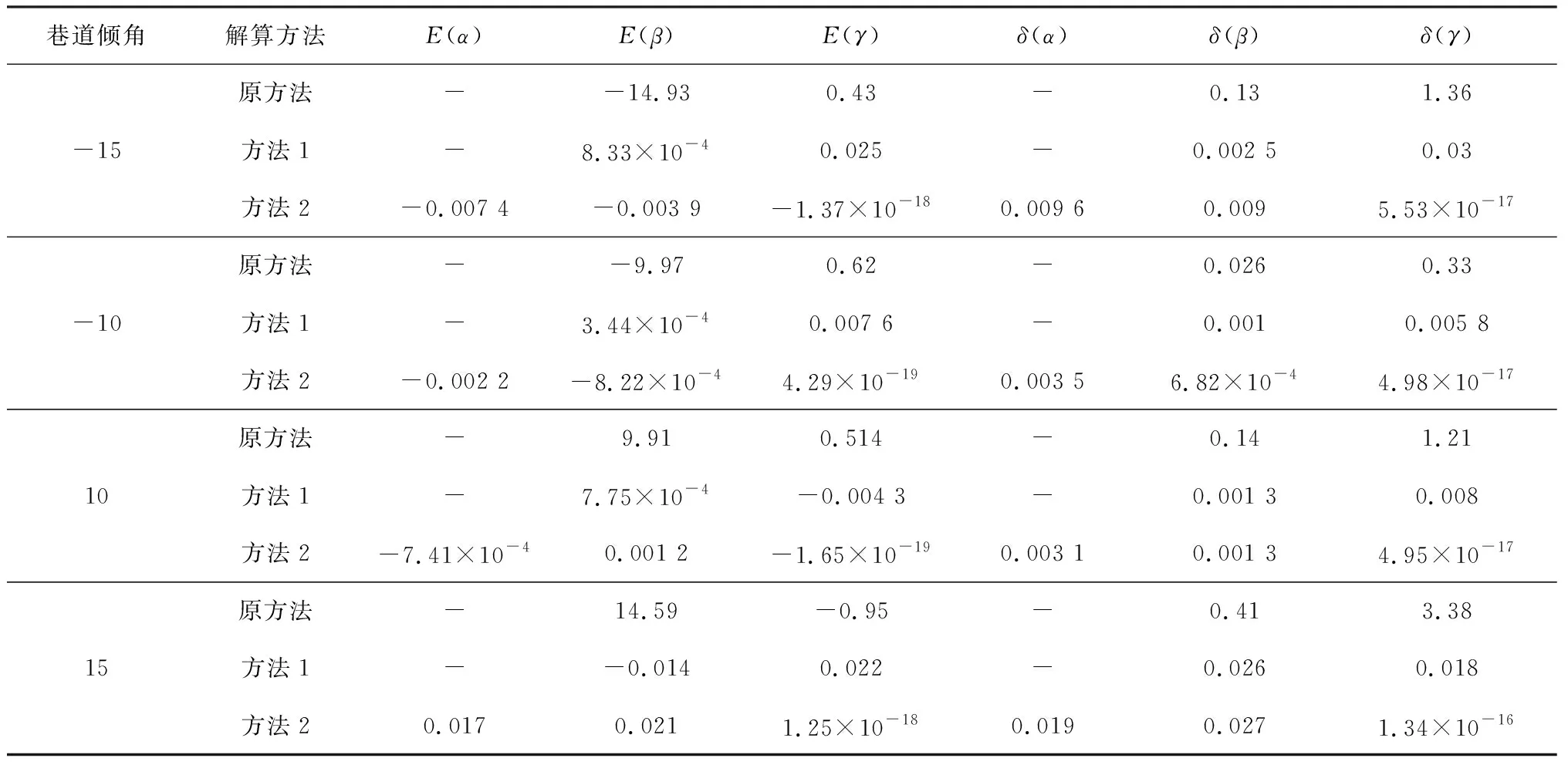
表2 倾斜巷道姿态参数测量误差均值与标准差Table 2 Mean and standard deviation of attitude parameter measurement error of inclined roadway (°)

5 结论

(1) 将双轴倾角仪的输出角度直接作为掘进机的俯仰角、横滚角会造成较大测量误差，需将双轴倾角仪与其他姿态参数测量方式融合，才能同时解算出掘进机全姿态参数。

(2) 给出了融合扇形激光和双轴倾角仪的姿态解算方法、融合机身两点坐标和双轴倾角仪的姿态解算方法。2种解算方法在模拟水平巷道中的最大误差均值为0.004 9°，在模拟倾斜巷道中的最大误差均值为0.025°，提高了掘进机基于双轴倾角仪的角度测量精度，扩大了双轴倾角仪的适用范围，使其可在掘进机倾斜巷道姿态参数测量中使用。

(3) 由于给出的2种位姿解算方法不需要使用高精度惯导等昂贵设备，所以在中小煤矿的掘进机智能化改造中具有较强的经济适用性。但是，本文旨在推导和验证2种掘进机姿态解算方法，所以未考虑各传感器的测量误差，下一步将结合测量误差对各组合传感器的测量值进行滤波处理。