基于改进复数矢量法的航母喷气偏流板装置运动分析

曹建平，孙文柱，王海东，王云翔

(海军航空大学青岛校区，山东 青岛 266041)

机构运动分析无论是对于新机械的优化设计，还是对于现有机械的运动性能分析，都是非常必要的[1]。机构运动分析方法一般分为图解法和解析法，其中解析法借助计算机可获得较高的计算精度并能直接用于机构优化设计，因而应用更为广泛。畅博彦等[2]针对筝形七杆机构采用几何证明的方式对机构执行构件实现直线运动的条件进行了研究。郭震等[3]采用解析法分析了刚性折纸机构的运动特性，推导出未知折痕转角的显式表达式。李杰[4]针对解析法推导过程复杂、难以得到解析解的问题，提出了一种面向机构运动分析的解析数值算法。但现有解析方法多基于闭环矢量方程进行几何分析，不够直观且易出错。复数矢量法直接采用代数方法求解几何方程，可有效解决上述问题，但经典的复数矢量法仅用于矢量的四则运算，不能求解矢量的点乘和叉乘，不利于复杂机构的运动分析，严重限制了复数矢量法的有效性。为此，本文对复数矢量法进行了针对性的改进，将复数运算扩展到矢量的点乘和叉乘，提高了复数矢量法的分析能力，并以喷气偏流板装置七杆机构为例进行了验证。

1 复数矢量法及其改进

复数矢量法是一种进行平面机构运动分析的经典解析方法，应用广泛[5-6]。其基本思想是利用复数符号表示平面矢量，从而将矢量的各种运算转换为复数的代数运算，利于运动分析与编程实现。

1.1 平面矢量及其复数表示

复数矢量法应用的对象是平面矢量，即在平面内既有大小又有方向的量。根据该定义，在同一平面内，位移、速度、加速度和力都是矢量，但矢量并不能完全表达其物理意义，比如要完全确定位移需要给出明确的起点和终点，而矢量只表达了位移的大小和方向；同样力的物理意义除了大小和方向以外还有作用点。换句话说，矢量除了表达物理量的大小和方向以外不表达任何其他要素，因此矢量可以在平面内进行二自由度的任意平移。另外，平面内的角速度、角加速度和力偶不是复数矢量法研究的矢量，原因在于这3个量虽然在物理意义上是有方向的，但其方向是垂直于作用平面的，利用正负号即可充分表达，因此可将其视为标量。

由定义可知，平面矢量本身与坐标系的选择是没有关系的，但可以在特定的坐标系内进行表示。如图1所示，AB表示一个矢量，其大小为LAB，方向与水平夹角为φAB，在直角坐标系OXY中可表示为：

AB=B-A=(xB-xA,yB-yA)

(1)

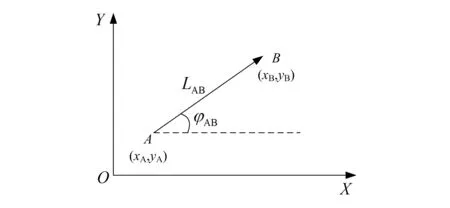
图1 平面矢量表示

由式(1)可知矢量对应于OXY平面的一个点，而复数与平面的点是一一对应的，因此可用复数来表示矢量：

AB=(xB-xA)+(yB-yA)i

(2)

进一步，矢量还可以表示为：

AB=LAB(cosφAB+isinφAB)

(3)

根据欧拉定理eiθ=cosθ+isinθ，式(3)可进一步表示为：

AB=LABeiφAB

(4)

式(4)即为平面矢量利用复数进行表示，进而矢量的代数运算可通过复数运算完成。设直角坐标系OXY内任意2个矢量为a1=(x1,y1)和a2=(x2,y2)，可分别用复数表示为a1=x1+y1i=L1eiφ1和a2=x2+y2i=L2eiφ2，其中L1和L2分别为a1和a2的大小，φ1和φ2分别为a1和a2与水平方向的夹角，则矢量加法表示为：

a1+a2=L1eiφ1+L2eiφ2

(5)

矢量减法表示为：

a1-a2=L1eiφ1-L2eiφ2

(6)

矢量标乘表示为：

ka1=kL1eiφ1

(7)

矢量微分表示为：

(8)

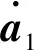
1.2 复数矢量法改进

经典的复数矢量法是不完善的，没有给出矢量点乘和叉乘的复数表示[1]，下面推导给出。

矢量点乘可表示为：

Re(L1L2ei(φ1-φ2))

(9)

式中Re(·)、(·)*分别表示复数的实部和共轭。

证明：根据矢量点乘定义，矢量点乘可表示为：

a1·a2=x1x2+y1y2

可得：

(x1+y1i)(x2+y2i)*=(x1+y1i)(x2-y2i)=x1x2+y1y2-x1y2i+x2y1i

则：

Re{(x1+y1i)(x2+y2i)*}=x1x2+y1y2

2018年5月，第四届现代家政产业创新发展研讨会在清华大学的熊知行楼召开，受到参会嘉宾的一致好评，在家政行业内引起积极的反响。在家政人的期待下，2018年11月24-25日，第四届现代家政产业创新发展研讨会孕婴童专题研讨在清华大学的熊知行楼进行，来自主办方单位负责人、职业院校研究学者、行业专家、行业从业人员近200人出席了本次活动。此次活动由全国妇联人才开发培训中心、《家庭服务》杂志社、清华大学老科协现代家政产业研究发展中心、北京市海淀区智慧社区与家庭服务协会主办。

证毕。

同理，矢量叉乘可表示为：

a1×a2=Im{(x1+y1i)(x2+y2i)*}=Im(L1L2ei(φ1-φ2))

(10)

式中Im(·)表示复数的虚部。需要注意的是，一般矢量的叉乘仍是矢量，但复数矢量法针对的是在同一平面的平面矢量，其叉乘得到的矢量的方向只能垂直于矢量所在平面，可用正负号来表示其方向，即可用标量完全表达，因此式(10)给出的矢量叉乘结果是标量。

2 喷气偏流板装置运动执行机构运动分析

2.1 机构描述

喷气偏流板(the jet blast deflector, JBD)是航母上保障舰载机安全连续起飞的关键设备，其作用是将舰载机起飞时由喷气发动机喷射出的高温高压气流向上、向外偏流，以保证人员、飞机和设备的安全[7]。喷气偏流板在组成上包括机械系统、海水冷却系统、液压系统和电气控制系统。美军现役航母上喷气偏流板装置有两种型号[8]，分别是MK7-1型和MK7-0/2型，其中MK7-1型有2组模块，MK7-0/2型则有3组模块，如图2所示。

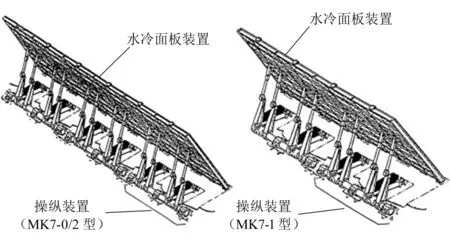
图2 美军MK7型喷气偏流板装置

无论是哪种型号，其机械系统的运动执行机构都是一种七连杆传动机构，其机构简图如图3所示。该机构包括6个活动构件，其中构件1是液压缸缸体，构件2是液压缸活塞，构件3是曲柄，构件5是旋转臂，构件6是连杆，构件7是偏流板组件，构件3和构件5固连在一起，构件2作为主动件；包括7个运动副，其中6个转动副，1个移动副。该机构实现将主动件2的往复移动转换为构件7绕着运动副F的升起/降下的往复转动。

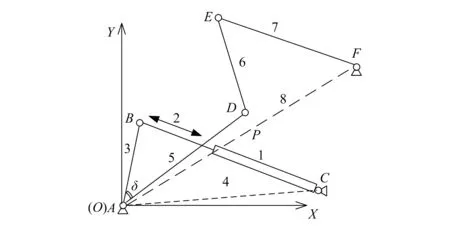
图3 喷气偏流板装置七连杆执行机构简图

2.2 机构运动分析

下面利用改进的复数矢量法对喷气偏流板运动执行机构进行运动分析。如图1所示，偏流板运动执行机构构成两个封闭矢量多边形：ABC和ADEF，据此可列出该机构的2个封闭矢量位置方程，用复数矢量表达如下：

(11)

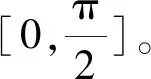
根据欧拉公式eiθ=cosθ+isinθ及图1所示相互位置关系(1和2受运动副约束共线，3和5固连在一起)，由式(1)可得(后文用c代表cos，s代表sin，ac代表arccos)：

(12)

式中：l1,l3,l4,l5,l6,l7,l8,δ,θ4,θ8为结构参数，是常量；l2,θ1,θ2,θ3,θ5,θ6,θ7为变化的结构参数变量。其中变量l2与原动件2相连，表示液压缸的活塞杆，其运动规律已知；其他6个变量是输出量，为待求量。

式(12)是非线性方程组，其解析解较难得到，但针对图3所示机构利用三角函数相关公式可得解析解：

(13)

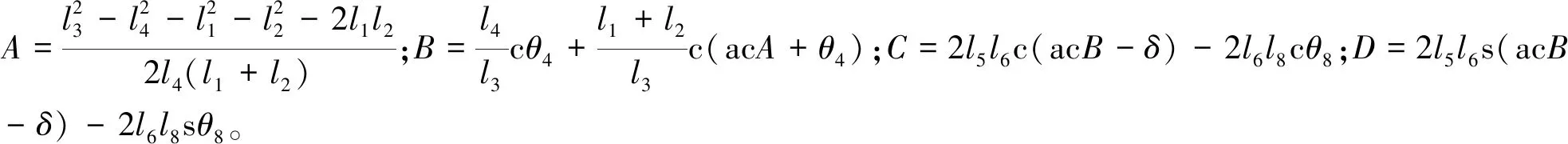
对式(13)求导，可得：

(14)

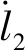
将式(14)写成矩阵形式：

(15)

对式(14)进一步求导，可得：

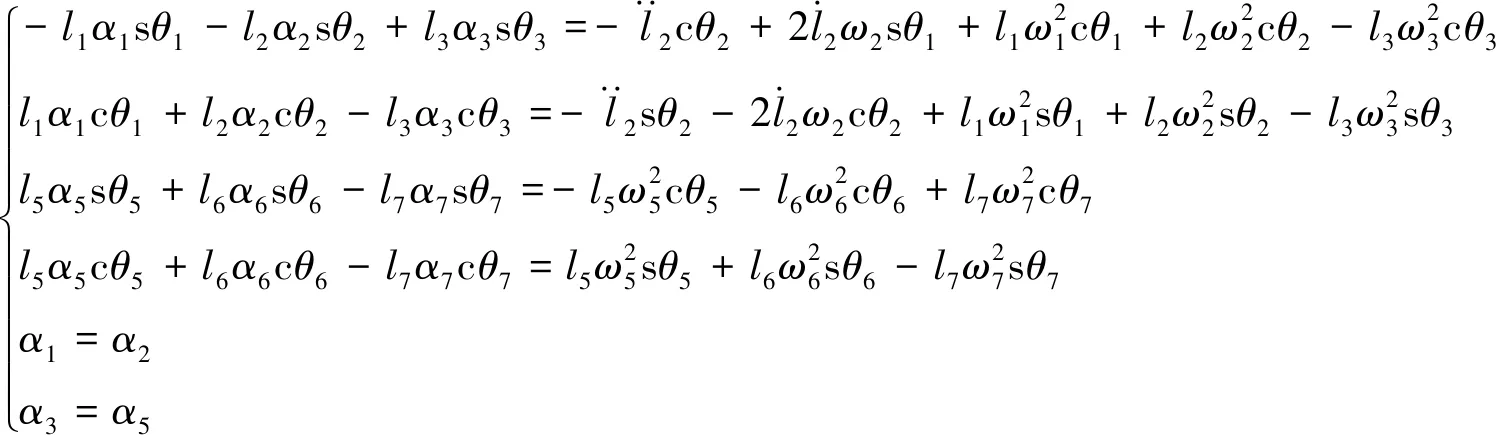
(16)

式中：αi(i=1,2,3,5,6,7)为角加速度。将式(16)写成矩阵形式：

(17)

3 算例分析

为分析航母偏流板装置运动特性，将图3所示机构结构参数设定为：安装角δ=40°，液压缸长度l1=1 200 mm，活塞杆初始伸出长度l20=200 mm，活塞杆行程Δl2=700 mm，曲柄长度l3=700 mm，舱室机架AC长度l4=1 700 mm，旋转臂长度l5=1 600 mm，连杆长度l6=1 500 mm，偏流板组件长度l7=2 800 mm，甲板机架AF长度l8=3 200 mm，舱室机架安装角θ4=1°，甲板机架安装角θ8=20°。

在以上结构参数基础上，采用MATLAB进行数值仿真，以l2为自变量，设间隔为0.01将其离散化仿真，并设定活塞杆做匀速往复运动，其速度大小为72 mm/s，分别代入公式(13)、(15)和(17)中，可得到如图4～6所示的各构件的位置线图、速度线图和加速度线图。

偏流板装置属于特大型船舶的特种装置，构件7偏流板组件自重可达上百吨，为减轻其升起和降下时对船体的冲击，设计上要求降低活塞杆行程末端的偏离板组件的运动速度。由图4可看出，偏流板组件7角速度先变大后变小，在末端时趋近于0，可有效避免强烈撞击，并利于制动，可知喷气偏流板装置七杆机构构型和设定结构参数基本达到了设计要求。

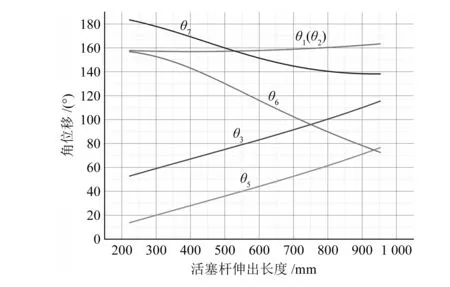
图4 位置线图

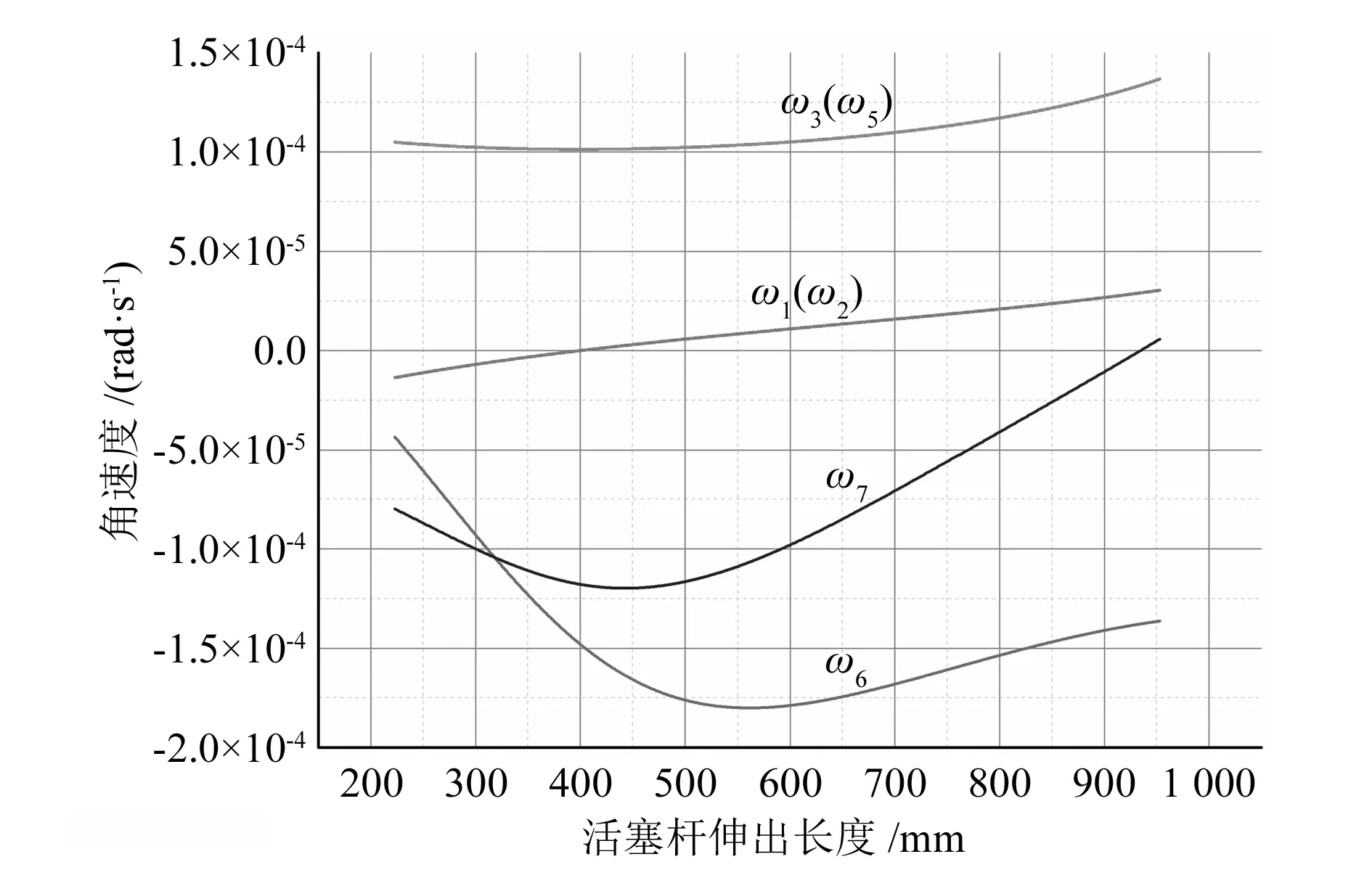
图5 速度线图

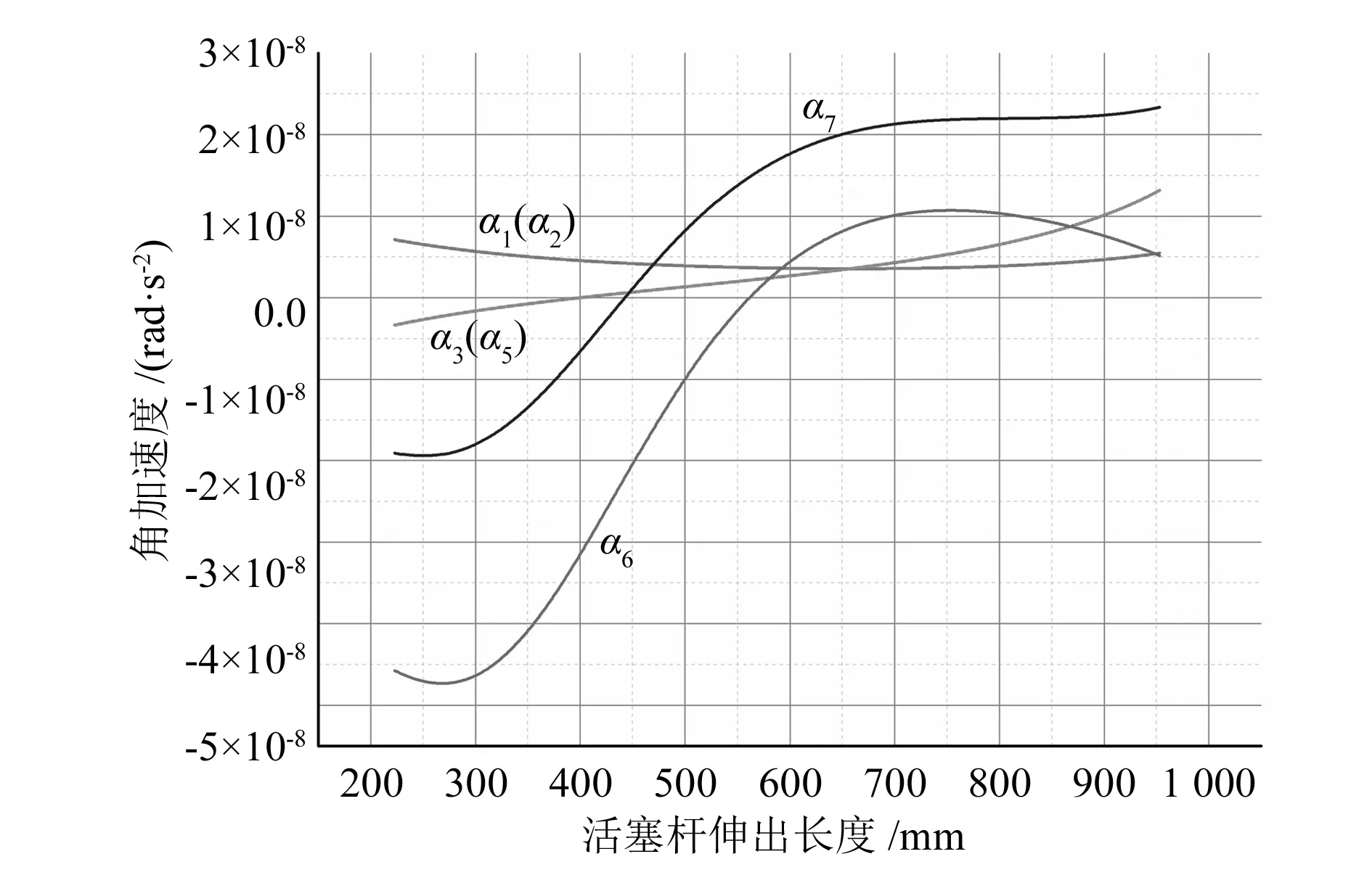
图6 加速度线图

4 结论

本文对经典的基于复数矢量法的平面机构解析方法进行改进，并应用到喷气偏流板七杆运动执行机构的运动分析中，可知：

1)改进后的复数矢量法不但可利用复数完成矢量常规四则运算，且可完成矢量的点乘和叉乘运算，为平面机构的运动学分析带来方便；

2)利用改进复数矢量法建立了喷气偏流板装置七杆机构的位置、速度和加速度方程，并得到解析解，说明了改进复数矢量法对于平面机构运动分析的有效性；

3)利用MATLAB对平面机构运动进行仿真，得到了机构的位置、速度和加速度线图，结果与设计要求相符，说明了结果的正确性；

4)本文结果为偏流板装置的构型和参数进一步优化设计奠定了理论基础。