偏流角修正对主动推扫成像品质影响分析

闫鑫 韩雪川 张永

（1 中国空间技术研究院 载人航天总体部，北京 100094）

（2 北京空间机电研究所，北京 100094）

0 引言

非沿迹主动推扫成像主要是卫星通过姿态机动、结合飞行地速建立某一特定的扫描速度，实现对某一条带或某一组一般轨迹目标的扫描成像；可快速获取某一方向的条带区域成像，提高卫星对海岸、边境、公路、铁路等关注目标的成像效率。可实现对任意地标轨迹的连续成像。它是一种应用前景非常广阔的工作模式，被认为是未来遥感成像的“倍增器”和热点技术，是国外先进的遥感卫星的必备技术之一、并已取得了实际应用。

针对采用时间延迟积分电荷耦合器件（time delayed and integration charged coupled device，TDICCD）进行扫描成像，其由于卫星高速运行与姿态机动，成像目标随地球自转等因素，使TDICCD线阵移动方向与目标像移方向会出现一定的角度偏差，导致偏流角的产生，降低相机 MTF和图像的分辨率，导致图像模糊，影响成像品质。

偏流角修正及其对图像品质影响，国内外学者已经进行了深入的研究，形成了丰富的研究成果。常规成像时，仅有地球自转运动、卫星姿态不变化的偏流角研究相对成熟，偏流角的产生机理和计算方法明确[1-2]，并针对偏流角修正方法开展了研究。针对TDICCD相机，文献[3]分析了偏流角对三线阵TDICCD相机的影响，文献[4]阐述了星下点成像及侧摆固定角度成像时偏流角计算，文献[5-6]分析了卫星姿态变化时的偏流角计算。针对偏流角修正，文献[7]提出采用在光学相机中加入偏流角调整机构实现偏流角调整，文献[1]采用整星偏航的方式修正偏流角。但偏流角修正不可避免的存在误差，无法实现完全补偿，影响成像品质。文献[8-11]通过计算成像调制传递函数（MTF）值，分析了偏流角及其修正误差对成像品质的影响。

上述的偏流角及其对成像品质的研究主要还是针对常规成像模式，针对非沿迹主动推扫成像模式的研究还未见有报道。因此，本文对非沿迹主动推扫成像的偏流角开展研究，建立偏流角计算及修正精度模型，通过分析偏流角修正精度对成像 MTF的影响评价对成像品质的影响，具有重要的实际价值和工程意义。

1 非沿迹主动推扫成像模型

偏流角的产生及修正与摄影地速直接相关，传统成像由轨道飞行速度和地球自转产生，非沿迹主动成像时，影响因素还包括姿态机动产生的速度。

1.1 摄影地速

传统遥感卫星对地成像时，相机视轴对地不变化，设VO为目标点线速度，地速V摄影是目标点线速度VO的相对速度与地球自转线速度Ve的合速度[12]，η为推扫方向与卫星飞行方向的夹角，如图1所示。

图1 摄影地速分析Fig.1 Photography land speed analysis

摄影地速可表示为：

非沿迹主动推扫成像时，相机推扫速度方向与卫星星下点速度方向不共线，从而导致摄影地速有别于传统摄影地速的定义，如图2所示。其中，S为卫星在轨道上的位置；M为成像目标点；L为卫星与目标点距离；O为星下点；T为侧摆点；a为卫星主动推扫角度。

图2 非沿迹主动推扫成像数学模型Fig.2 Model of no-along trajectory active push-sweeping imaging

由图2可知，摄影地速V摄影是载荷视轴推扫线速度Vη、地球自转线速度Ve和目标点M相对卫星在轨运动的相对速度的合速度：

式（2）转换为矢量方程如下式所示：

设摄影地速在大地坐标系的矢量为[ ]Tx y z ；i，o分别表示矢量在惯性系和轨道下的描述；Cid为惯性坐标系与大地坐标系的转换矩阵；Coi为轨道坐标系与惯性坐标系的转换矩阵。R为地球半径在惯性系下矢量；eω为地球自转角速度；oω为卫星星下点相对地心的运行角速度；ηω为光学相机的推扫速度。

1.2 积分时间

低轨遥感卫星相机采用TDICCD成像，积分时间是很重要的成像参数，敏捷工作模式的积分时间设置与遥感卫星积分时间设置有很大不同，卫星进行主动推扫模式成像时，表现为“动中成像”[13]，观测斜距、相面扫描速度变化剧烈，导致积分时间快速变化，对成像品质影响较大。

积分时间计算如下：

式中 Tint为积分时间；l为 TDICCD的像元尺寸；f为星上相机的焦距；vr为卫星本体系内目标区域相对像平面移动速度；vl为像面上像移速度。

2 偏流角修正

2.1 传统偏流角修正及精度

（1）偏流角修正

传统卫星对地成像过程中，相机光轴对地指向保持不变，与卫星星下点运动方向相同，此时产生的偏流角主要是由于目标点的地球自转线速度造成的，如图3所示。

图3 偏流角示意Fig.3 Drift angle schematic diagram

星下点速度与相机速度一致的情况下，偏流角为星下点速度与目标速度（星下点速度与地球自转速度的合速度）的夹角β可描述为：

式中 Vp2、Vp1分别为合速度的横向分量和纵向分量；传统模式成像时，卫星三轴姿态指向固定，推扫方向与卫星飞行方向的夹角η不变，随着目标地纬度的增加，地球自转线速度减小，造成偏流横向分量减小，偏流角相应减小。

（2）偏流角修正精度

偏流角修正精度取决于对成像品质的要求、相机载荷参数等因素。设偏流角修正精度为Δφ；相机积分级数为N；若用户要求横向偏差允许最大剩余量为ΔL2，则有关系：

由此确定偏流角修正精度Δφ。

2.2 推扫成像偏流角修正及精度

与传统的被动式推扫成像不同，非沿迹主动推扫成像过程中载荷视轴指向不断变化，在成像某一时刻，当前目标区域点位M，不计偏流角的影响时，下一时刻的目标点应为M1，但由于星下点相对线速度和地球自转线速度的影响，产生了偏流效应，导致下一时刻目标点偏离到M2，如图4所示。

图4 非沿迹主动推扫成像偏流角Fig.4 Drift angle of no-along trajectory active push-sweeping imaging

设卫星轨道六要素为轨道倾角i；升交点赤经Ω；轨道高度为h；偏心率e；真近点角fsat；近地点幅角ωsat。

图5 非沿迹主动推扫成像偏流角计算Fig.5 Drift angle calculation of no-along trajectory active push-sweeping imaging

图5中， Osxoyozo为卫星的轨道坐标系（O系）； OexIyIzI为地心惯性坐标系；Oc为相机坐标原点。图中各位置矢量关系如下：

式中 Rst为由卫星质心指向目标点T的矢量；Ret为由地心指向侧摆点T的矢量；Res为地心指向卫星质心的矢量；Rct为卫星相机载荷像中心至目标点T的矢量；Rsc为卫星质心指向相机载荷像中心的矢量。

将矢量Rst在轨道坐标系（O系）下表示有：

将矢量Rst在卫星本体坐标系（b系）下表示为：，AbO表示轨道坐标系O系到b系的转换矩阵。

将Rct在相机坐标系（c系）下表示为：

对公式（10）两边求导，因为相机安装位置固定，所以有：

因而，

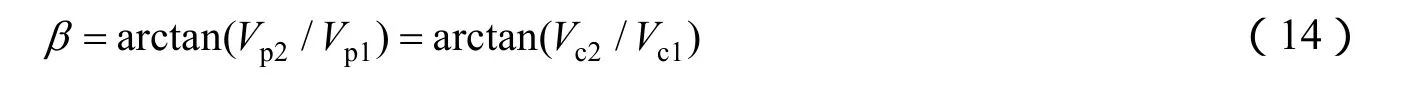
3 成像品质影响

TDICCD相机的特点要求曝光控制与卫星飞行速度同步。如果有误差，TDI的多级CCD像元不能精确对同一目标成相[14]。像移是影响星载TDICCD相机成像品质的重要因素[15]。定义单级不同步误差产生的像移为Δφ，则N级积分造成的调制传递函数可以近似表示为：

式中 v为所成图像的空间频率，一个积分周期内由偏流角造成的像移Δφ为[8]：

式中 β为偏流角；l为像元尺寸。

TDICCD线阵对与飞行方向不垂直的角度误差很敏感，要求线阵与飞行方向的垂直精度很高才能保证照相相质。其调制传递函数可以近似表示为：

工程上，目前技术条件下，为保证成像品质，一般要求光学系统成像MTF值达到0.9的水平

4 仿真分析

为进行非沿迹主动推扫成像的偏流角计算及修正前后对成像品质的影响分析，设定航天器轨道高度400km，轨道倾角42.7°，分别计算推扫角度、推扫角速度、推扫方向与卫星飞行方向夹角η变化时偏流角随目标点地理纬度变化，同时，进行成像MTF计算时，选择像元尺寸7μm，积分级数选择为96级，目标点地理纬度选取–100°～100°。仿真结果如下：

（1）不同推扫角度和角速度的影响分析

某一时刻，推扫角度分别取值为0°、10°、20°、30°，图2中η角分别取值120°，推扫角速度1.5（°）/s，用于描述非沿迹主动推扫，得到随目标点地理纬度变化的偏流角及对应MTF值分别如图6和图7所示；推扫角度分别取值为20°，图2中η角分别取值120°，推扫角速度2（°）/s、4（°）/s、6（°）/s、8（°）/s，不同地理纬度对应的偏流角及对应MTF值分别如图8和图9所示，对应成像MTF值分别如7、图9所示，这里仅给出目标点地理纬度在–100°～0°范围的仿真结果，地理纬度0°～100°范围的偏流角仿真结果与之相对于0°纬度对称。

图6 推扫角度不同时的偏流角Fig.6 Drift angle of different push-sweeping angles

图7 偏流角对应的MTF值Fig.7 MTF of drift angle

图8 推扫角速度不同时的偏流角Fig.8 Drift angle of different push-sweeping angular rate

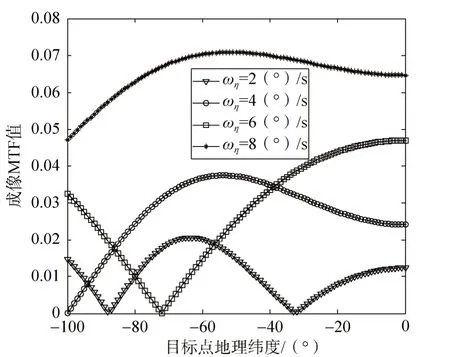
图9 偏流角对应的MTF值Fig.9 MTF of drift angle

由图6可知，仅推扫角度变化时，随着推扫角度增加，同一地理纬度对应的偏流角逐渐减小，且减小的幅度随着推扫角度变化逐渐增大；同时，从图6、图8可以看出，同一推扫角度时，目标点地理纬度越小，对应的偏流角越小，0°时偏流角最小，航天器需具备不小于25.3°的偏流角修正能力；由图8可知，仅推扫角速度变化时，随着推扫角速度增加，同一地理纬度对应的偏流角逐渐减小，且减小的幅度随着推扫角度变化逐渐减小，此种条件下，航天器需要具备不小于19.2°的偏流角修正能力。

对于偏流角对成像MTF值的影响，由图7、图9可知，存在图6、图8所示偏流情况下，成像MTF值不大于0.02、0.08，与成像品质所需要的至少0.9的MTF值相比，无法满足成像要求，因此需要进行偏流角修正，且从图7、图9可知，偏流角越小，对应的MTF值越高。

（2）不同η角的影响分析

某一时刻，推扫角度分别取值为20°，推扫角速度2（°）/s，图2中η角分别取值100°、120°、140°、160°，不同地理纬度对应的偏流角和对应MTF分别如图10和图11所示；同时，为了阐述垂直于非沿迹主动推扫时漂流角与垂直于迹向推扫的不同，选择η为90°进行仿真，并与非沿迹时η为120°时进行对比，仿真结果如图12和图13所示。

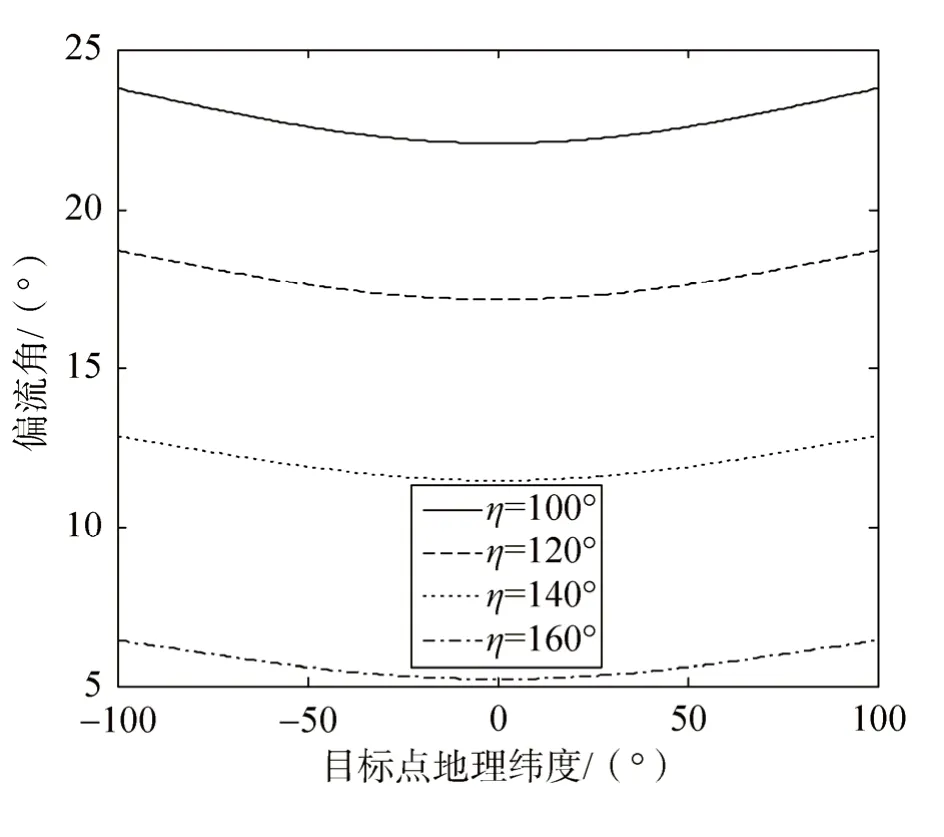
图10 η角不同时的偏流角Fig.10 Drift angle of different η

图11 偏流角对应MTF值Fig.11 MTF of drift angle

图12 垂直于迹向推扫（η=90°）时偏流角Fig.12 Drift angle with push-sweeping vertical trace

图13 偏流角对应MTF值Fig.13 MTF of drift angle

由图10、图12可知，针对非沿迹主动推扫成像，推扫角度和角速度不变，仅η角变化时，同一目标点纬度对应偏流角随着 η角增加（η＞90°）逐渐减小，且减小幅度逐渐加快，航天器需要具备不小于 24.1°的偏流角修正能力；垂直于迹向进行推扫成像时（η=90°）时，偏流角明显大于非沿迹主动推扫成像（η＞90°），航天器需要具备不小于 26°的偏流角修正能力，说明垂直于迹向进行推扫成像时偏流角最大。

同样，η角变化时，在图10、图12所示偏流角的情况下，成像MTF值最大不超过0.08，对于垂直于轨迹的情况，其最大MTF不超过0.015，无法满足成像任务对MTF达到0.9以上的要求，需要采取措施对偏流角实施补偿。

为分析偏流角修正精度对成像品质的影响，参考目前高精度遥感任务，设定成像品质要求横向允许像移量不超过0.2个像元，则对应不同TDI积分级数需要的偏流角修正精度如表1所示。

表1 不同积分级数对应偏流角修正精度Tab.1 Drift angle correction precision of different integral series

5 结束语

针对非沿迹主动推扫成像时的偏流角修正及对成像品质的影响，明确了非沿迹主动推扫成像的定义，建立了有别于传统成像模式的摄影地速计算模型，完成了该模式下偏流角计算的数学建模，开展了偏流角对成像 MTF影响的分析，并基于以上工作，完成了卫星在不同推扫角度、推扫角速度、与迹向不同角度时偏流角和成像MTF值的计算与仿真分析，仿真结果表明：推扫角度在0°～30°之间、推扫角速度不超8（°）/s、与迹向成90°～160°进行推扫成像，对应的偏流角最大接近26°，成像MTF值不超过0.08，与工程上要求的MTF值最低不小于0.9的要求差距较大，不进行偏流角补偿的情况下，无法满足工程需要。该分析方法综合考虑了任务及载荷特征参数，可用于未来非沿迹主动推扫成像的任务分析，具备实际的工程意义。

（

）

[1] 袁孝康. 星载TDICCD推扫相机的偏流角计算与补偿[J]. 上海航天, 2006, 23（6）: 10-13. YUAN Xiaokang. Calculation and Compensation for the Deviant Angle of Satellite Borne TDICCD Push Scan Camera[J]. Aerospace Shanghai, 2006, 23（6）: 10-13. （in Chinese）

[2] 胡莘, 曹喜滨. 三线阵测绘卫星的偏流角改正问题[J]. 测绘科学技术学报, 2006, 23（5）: 321-324. HU Xin, CAO Xibin. The Correction of Drift Angle of the Three-line Array Mapping Satellite[J]. Journal of Zhengzhou Institute of Surverying Mappingan, 2006, 23（5）: 321-324. （in Chinese）

[3] 杨居奎, 许敬旺. 偏流角对三线阵TDICCD测绘相机的影响分析[J]. 航天返回与遥感, 2006, 27（4）: 27-32. YANG Jukui, XU Jingwang. The Effect of the Drift Angle on Three-line TDICCD Mapping Camera[J]. Spacecraft Recovery & Remote Sensing, 2006, 27（4）: 27-32. （in Chinese）

[4] 景泉. 敏捷卫星偏流角计算模型研究[J]. 航天器工程, 2012, 21（4）, 16-20. JING Quan. Research on Computation Model of Bias Angle for Agile Satellite[J]. Spacecraft Engineering, 2012, 21（4）, 16-20. （in Chinese）

[5] 黄群东, 杨芳, 赵键. 姿态对地指向不断变化成像时的偏流角分析[J]. 宇航学报, 2012, 33（10）: 1544-1551. HUANG Qundong, YANG Fang, ZHAO Jiang. Drift Angle Analysis for Agile Satellite Imaging When Its Attitude Points to the Earth Changing Continuously[J]. Journal of Astronautics, 2012, 33（10）: 1544-1551. （in Chinese）

[6] 黄群东, 杨芳, 赵键. 姿态对地指向不断变化成像时的像移速度计算[J]. 光学精密工程, 2012, 20（12）: 2812-2820. HUANG Qundong, YANG Fang,ZHAO Jiang. Calculation of Image Motion Velocity for Agile Satellite Dynamic Imaging to Changed Continuously Attitude Point[J]. Optics and Precision Engineering, 2012, 20（12）: 2812-2820. （in Chinese）

[7] 李友一. 空间相机中的偏流角控制[J]. 光学精密工程, 2002, 10（4）: 402-406. LI Youyi. Study of the Drift Angle Control in a Space camera[J]. Optics and Precision Engineering , 2002, 10（4）:402-406.（in Chinese）

[8] 杨秀彬, 贺小军, 张刘, 等. 偏流角误差对TDICCD相机成像的影响与仿真[J]. 光电工程, 2008, 35（11）: 45-50. YANG Xiubin, HE Xiaojun, ZHANG Liu, et al. Effect and Simulation of the Deviant Angle Error on TDI CCD Cameras Image[J]. Opto-electronic Engineering, 2008, 35 （11）: 45-50. （in Chinese）

[9] 晋利兵, 马文坡, 唐绍凡, 等. 偏流角对品字形拼接探测器成像的影响[J]. 航天返回与遥感, 2014, 35（2）: 69-75. JIN Libing, MA Wenpo, TANG Shaofan. et al. Effect of the Drift Angle on Imaging of Three Non-collinear CCD Chips[J]. Spacecraft Recovery & Remote Sensing, 2014, 35（2）: 69-75. （in Chinese）

[10] 李晓云, 杜伟. 星载TDICCD相机像移对成像质量的影响分析[J]. 航天器工程, 2011, 20（3）: 51-55. LI Xiaoyun, DU Wei. Analysis of Image Motion Effect on Satellite TDICCD Camera Image Quality[J]. Spacecraft Engineering, 2011, 20（3）: 51-55. （in Chinese）

[11] 攀超, 李英才, 易红伟. 偏流角对TDICCD相机像质的影响分析[J]. 光电工程, 2007, 34（9）: 70-74. PAN Chao, LI Yingcai, YI Hongwei. Influence Analysis of Drift Angle on Image Quality of TDICCD camera [J]. Opto-electronic Engineering, 2007, 34（9）: 70-74. （in Chinese）

[12] 陈绍龙. 侧摆摄影偏流角和速高比的计算模型[J]. 航天器工程, 2010, 19（1）: 36-40. CHEN Shaolong. Computation Model of Veer Angle and Velocity-Height Ratio for Space Camera in Roll Attitude [J]. Spacecraft Engineering, 2010, 19（1）: 36-40. （in Chinese）

[13] JEAN J, ERIC J, GERARD L, et al. Attitude Duidance Technics Developed in CENS for Earth Observation and Scientific Missions[C]. The 28thAnnual AAS Guidance and Control conference, Breckeridge, 2005: 11-16.

[14] MIKKER B M, RUBINOVICH EY. Image Motion Compensation at Charge-coupled Device Photographing in Delay-integration Mode [J]. Automatic and Remote Control, 2007, 68（3）: 11-16.

[15] 庄绪霞, 王治乐, 阮宁娟, 等. 像移对星载 TDICCD相机成像品质的影响分析[J]. 航天返回与遥感, 2013, 34（6）: 66-73. ZHUANG Xuxia, WANG Zhile, RUAN Ningjuan, et al. Influence Analysis of Image Motion on Image Quality of Satellite-board TDI Camera Optical System[J]. Spacecraft Recovery & Remote Sensing, 2013, 34（6）: 66-73. （in Chinese）