机器人髋关节步态控制方法的研究

王瑜瑜，刘少军

(西安航空职业技术学院通用航空学院，陕西 西安 710089)

仿人机器人在实际的运动行走过程中，由于自身以及环境等各种因素的共同作用，致使行走的实际运动轨迹和设定的轨迹没有完全重合，各关节角度和设定角度之间亦存在偏差[1-2]。上述因素皆会对机器人行走的稳定性产生影响，情况严重时会导致机器人跌倒乃至毁坏，故机器人研讨探究的难点之一即是保持行走过程的稳定性[3]。通过已有的研究可知，若机器人的零力矩点(ZMP)处于支撑多边形的边缘，此时机器人身处极易摔倒的临界状态，这种情况是应该尽量避免的[4-5]。因此，应该考虑加入适当的控制方法，使得机器人的零力矩点由支撑多边形的边缘往中心移动，以确保机器人平稳行走，提高系统的稳定性和鲁棒性。通过分析研究，笔者提出了一种基于机器人姿态的髋关节补偿控制方法。

1 机器人的姿态计算

仿人机器人的姿态参数主要表现为躯干的横滚角和俯仰角，这两个参数的变化直接反映机器人躯体姿态的改变。故要完成机器人躯干姿态的计算，首要的是建立躯干的参考坐标系，具体如图1所示，位于该参考坐标系下的姿态角度如图2所示。其中，AngleX和AngleY分别为机器人躯干绕X轴和Y轴的偏转角，即分别代表躯干的横滚角与俯仰角。

图1 躯干参考坐标示意图

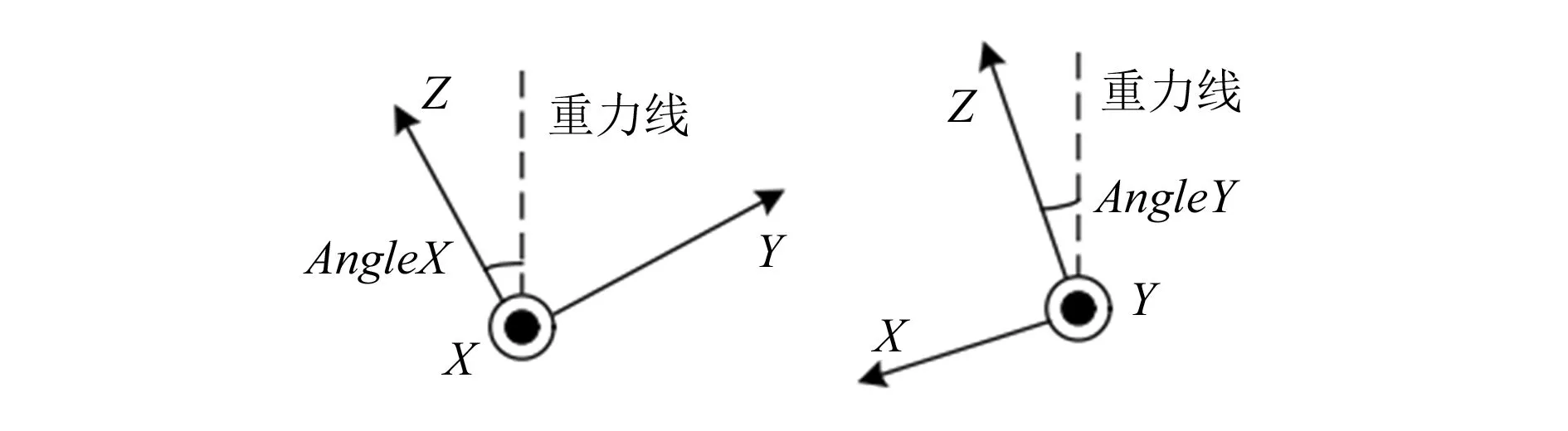
图2 躯干坐标系下的姿态角度

NAO机器人自身带有惯性单元，该单元包含了一个用于计算姿态变化角速度值的三轴陀螺仪和一个用于获取运动加速度值的三轴加速度计[6]。由于二者都存在测量误差，若采用直接融合反馈值方式会致使偏差累加，故本文采用了卡尔曼(Kalman)滤波方式，实现两种传感器信号数据的有机融合，进而估算出机器人的姿态角度[7-8]。Kalman滤波具体步骤为：

1)系统预估状态方程：

(1)

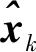
2)预估协方差矩阵：

(2)

3)Kalman增益滤波：

(3)

式中：Kk为卡尔曼增益；H为观测矩阵；R为测量的协方差。

4)由观测的数据先验估计值：

(4)

式中：xk为k时刻的系统状态；Zk为k时刻测量矩阵。

5)估计均方差：

(5)

式中：I为与状态向量同维度的单位矩阵。

由于机器人在前向和横向两个平面内的运动是相互独立的，因此这里以前向平面为例进行介绍。

设加速计的测量值为：

a=[axayaz]

(6)

式中：a为加速度测量值；ax，ay，az为x，y，z轴加速度值。

据此可得到机器人行走过程中的躯干倾角θ(t)为：

(7)

利用陀螺仪获取躯干的角速度ω，对该角速度进行积分运算便同样可获得躯干倾角为：

(8)

式中：t为时间；T为机器人步态的单步周期。

考虑到实际噪声影响，将式(8)实施离散化处理后可得：

θk+1=θk+ωkT+w

(9)

式中：θk+1为(k+1)时刻躯干倾角；ωk为k时刻躯干角速度；w为过程噪声。

根据状态转换方程的定义选取系统状态变量x：

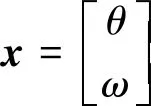
(10)

由式(9)和式(10)可得，状态方程为：

(11)

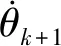
从惯性单元获得俯仰角的角度及角速度为：

(12)

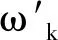
2 倾角髋关节补偿控制

2.1 姿态补偿控制器

机器人行走步态控制的主要作用就是调整各关节角度，以保证机器人处于动态稳定状态。机器人髋关节是其上肢与下肢连接的枢纽，也是上半身质量空间位置分布的主要控制关节。由ZMP定义可知，髋关节能直接影响机器人倒立摆模型的质心位置，而该质心位置分布会对机器人稳定性直接造成影响[9-10]。故而为了提高系统稳定性，本文采用了髋关节补偿控制方法，其控制结构如图3所示。

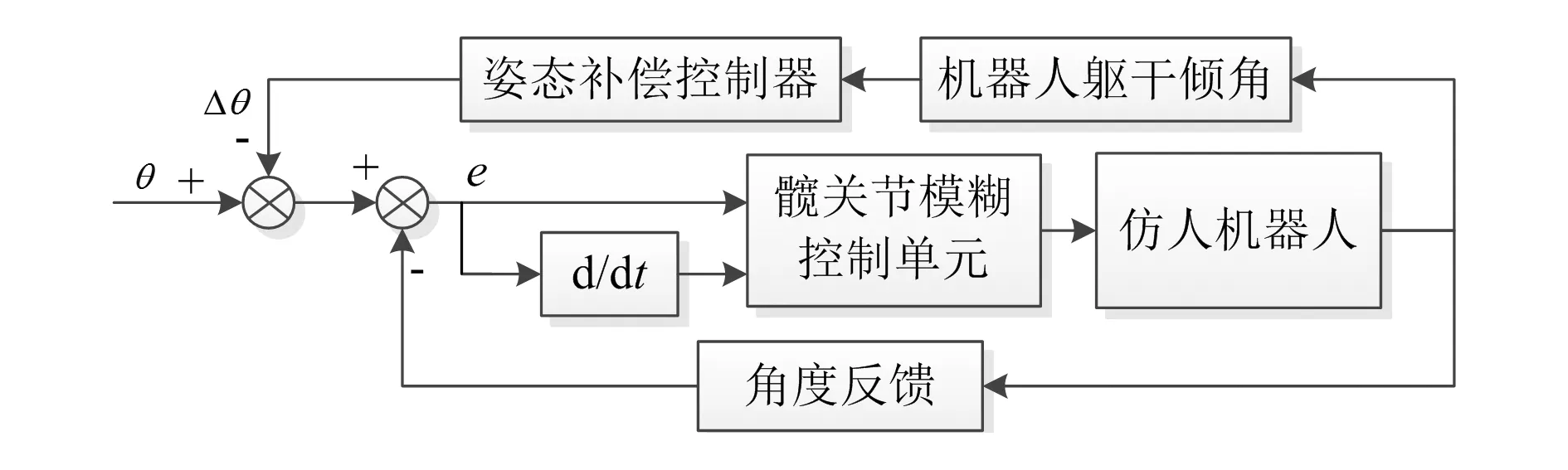
图3 髋关节的稳定补偿控制结构图

由图可知，当机器人躯干发生倾斜时，会将获取的躯干倾角传送给姿态补偿控制器，控制器输出髋关节补偿角Δθ，从而实现对躯干的运动控制，其中控制单元采用模糊控制规律。补偿角Δθhip的计算如图4所示。

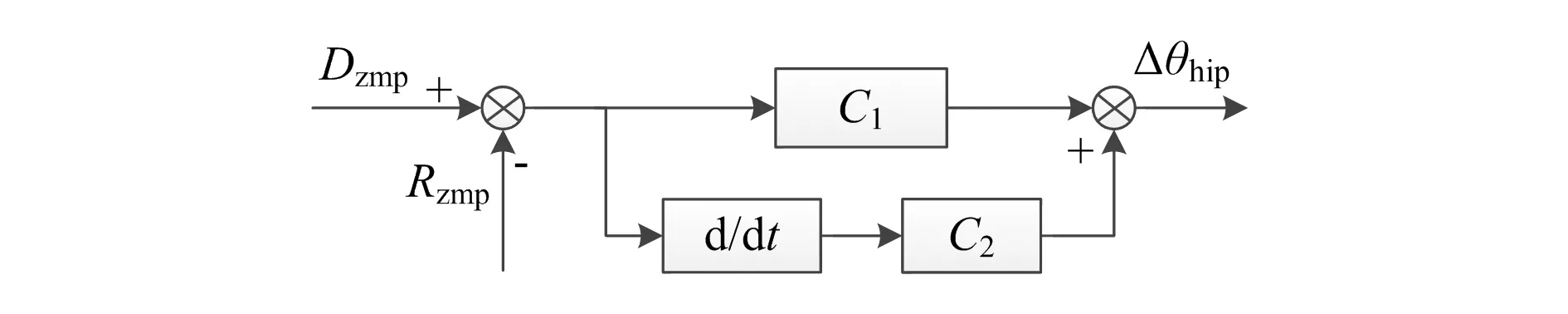
图4 姿态补偿控制器

图中，Dzmp为机器人倾角的期望值，Rzmp为机器人倾角的实际值，髋关节角度补偿计算公式为：

(13)

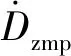
2.2 模糊控制器

控制器将补偿后的角度偏差以及偏差变化率视为输入信号，根据补偿角度、角度误差及其变化率的实际范围，初定角度误差的基本论域为(-6°,6°)。在此基础上，为了将控制器进行标准化设计，变化区间定为[-6,+6]，将该区间进行离散化处理后可得由13个整数元素组成的集合：{-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6}。

若论域范围为[a,b]，则可利用式(14)将变量x转换成论域范围为[-6,6]的变量y。

(14)

为了对变量的状态进行准确描述，设定了以下7个符号：正大(PB)、正中(PM)、正小(PS)、零(ZE)、负小(NS)、负中(NM)、负大(NB)。将它们与前面的论域结合便可得模糊隶属函数，具体如图5所示。用上述7个符号将系统的两个输入变量进行列写，可得如表1所示的模糊控制规则表，利用该表即可得与输入量相统一的模糊控制规则。

表1 模糊控制规则表

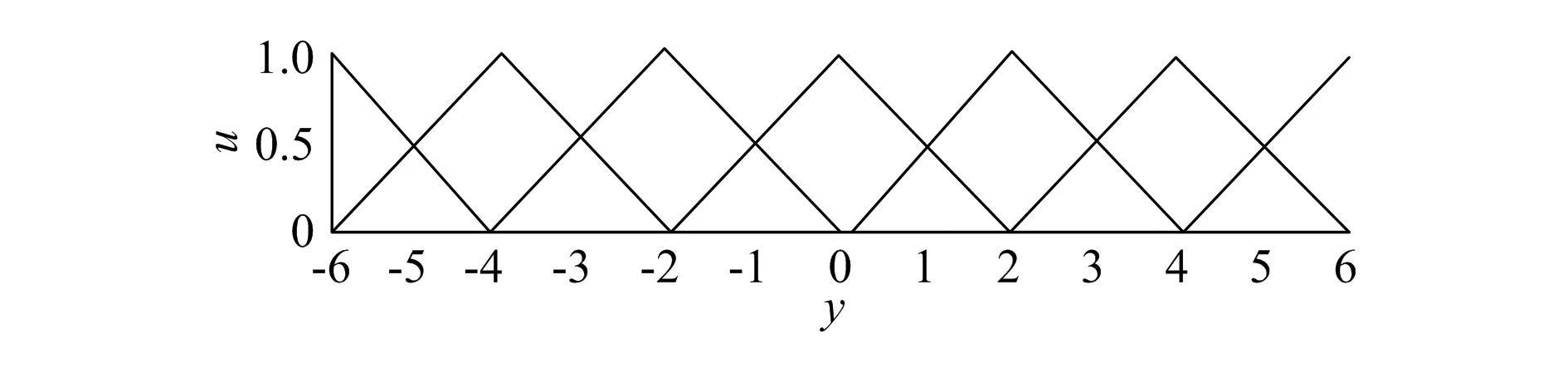
图5 模糊状态变量隶属函数

3 实验结果及分析

3.1 动态轨迹跟踪控制实验

首先进行机器人轨迹跟踪实验，由图6可知，加入补偿控制前，运动轨迹跟踪的相对误差在(-10%,10%)发生较大幅度变化，而加入补偿控制后运动轨迹跟踪误差变小，降低至(-3%,3%)，且跟踪的稳定性明显增强。由图7平均相对控制量的输出结果可知，补偿控制的加入使得控制量明显增加，相应的控制效果明显增强。

图6 位置轨迹跟踪的平均相对误差

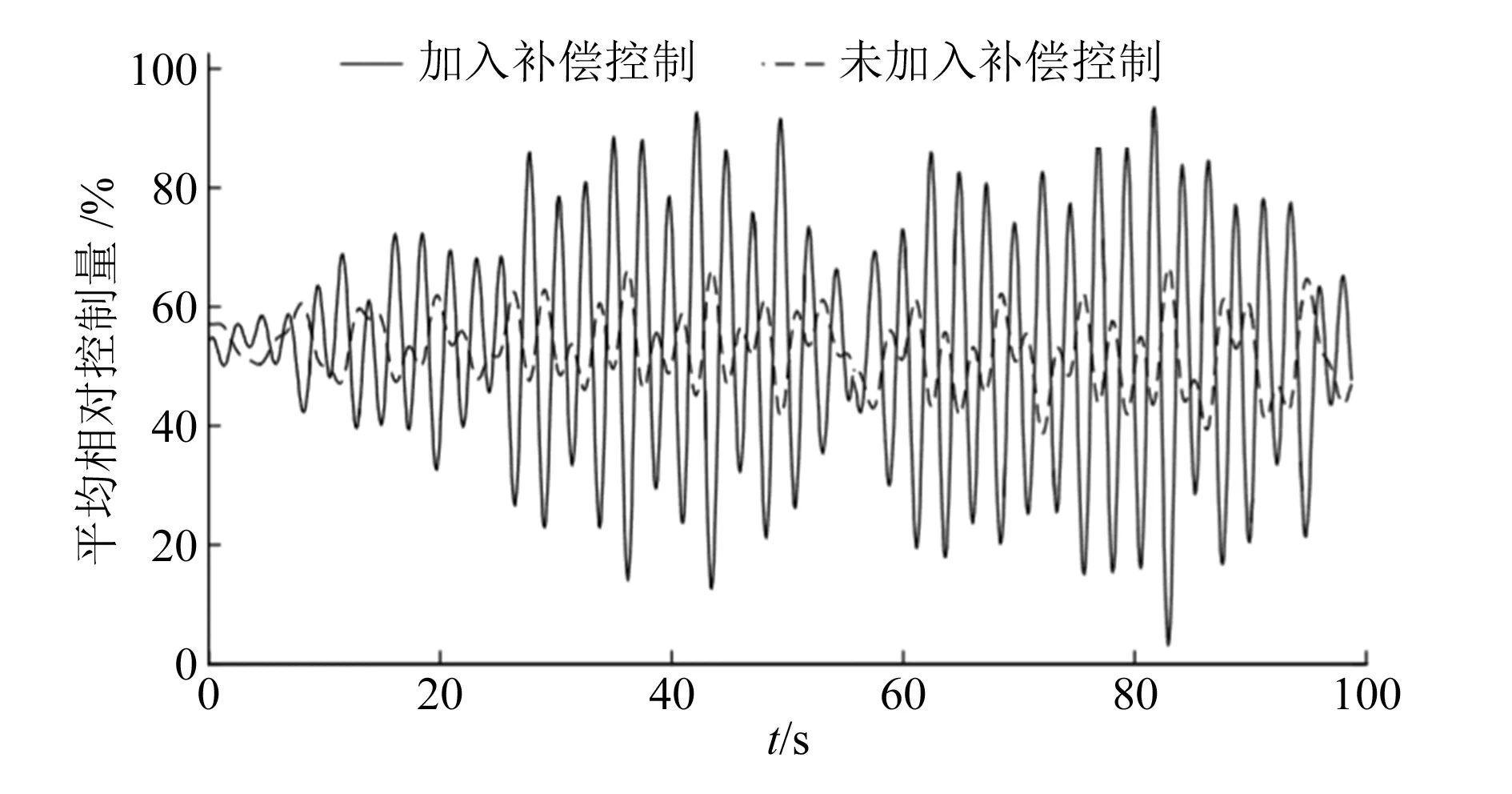
图7 平均相对控制量

3.2 倾角测试实验

图8 机器人行走过程中倾角值的变化

由补偿前后的数据波形可知，加入补偿后不仅使得机器人倾角摆动幅度减小，而且极大缩小了角度的变化范围，能有效防止倾角过大现象的出现。

计算获得的补偿前后躯干倾角误差的统计结果见表2，躯干倾角补偿前后ZMP偏移期望值的统计结果见表3。

表2 补偿前后躯干倾角误差的统计结果

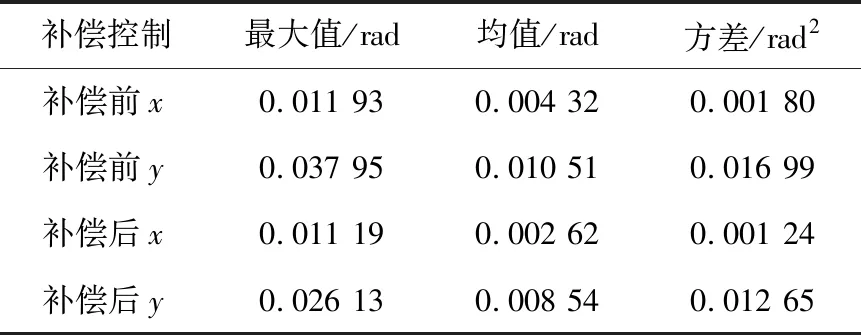
表3 躯干倾角补偿前后ZMP偏移期望值的统计结果

由表2和表3的统计数据可知：实施补偿后能够有效降低机器人运动过程中发生的倾斜角度；躯干的补偿作用对于ZMP在y方向的作用效果尤为明显；有效提高了机器人行走的稳定性，同时极大增强了步态的鲁棒性。

4 结束语

本文从机器人髋关节能直接影响倒立摆模型质心轨迹的角度出发，设计、分析了基于模糊控制的姿态髋关节补偿控制策略。利用加速度计和陀螺仪构成惯性单元计算躯干的倾角，在此基础上，采用姿态角度对髋关节进行补偿，并采用模糊控制算法进行控制，达成了机器人稳定步态行走的效果。最后的实验结果也充分证明了本文所提控制方法的有效性和可行性。