高速铁路无砟轨道-路基动应力特性分析

柳厚祥，朱性彬

（长沙理工大学 土木工程学院，湖南 长沙 410114）

高速铁路相当快捷，但高速列车轴重增大、速度提高，必然导致轨道-路基系统的动力相互作用更为复杂，高速铁路路基的动力特性、车-路耦合振动等已成为重要的研究内容[1]。

高速荷载下地基动力响应主要包括地基的动应力、动应变和动加速度，而在铁路路基设计中主要考虑路基的强度和变形。国内外学者对铁路进行了路基变形控制、路基动力特性及车-路耦合振动等研究。Kouroussis 等人[2]使用有限元方法在时域中开发了一个3D 模型，用于土壤的垂直轨道动力耦合。Connolly等人[3]也提出了3D-FEM 模型，可模拟轮轨界面处的非线性及地面振动，但计算成本高。李扬波等人[4]通过模型计算与室内足尺无砟轨道-路基模型试验，研究了轨道部件刚度、弹性模型等因素对路基动力的影响。冯青松等人[5]采用多体动力学和有限元方法建立有轨电车车辆模型和嵌入式轨道路基地基，将通过车辆模型获取的动态轮轨垂向力施加在轨道路基地基模型上，研究有轨电车轨道路基结构中的动应力。郭志广等人[6]在武广高速铁路咸宁试验段路基断面埋设元件，并在“联调联试”阶段和运营阶段分别对动车组荷载下的路基动力响应进行现场测试，并采用时域幅值分析、小波分析等方法对路基振动特性进行研究。聂如宋等人[7]在朔黄重载铁路的路桥过渡段路基开展了现场动力响应测试，获得了列车运行条件下路肩及路基边坡的动位移响应数据。但这些研究未能系统分析动应力幅值在路基各层内沿线路3个方向的分布及衰减，且选取地基尺寸均较小，未能有效反映波动的空间传播[8]。因此，作者拟研究铁路路基竖向动应力沿线路竖向、横向和纵向的分布规律，其计算点均位于线路中心线正下方。

1 数值分析模型

1.1 模型概况

轨道-路基空间耦合模型如图1 所示。模型选择规范标准60 kg/m 的钢轨和CRTSⅠⅠ型无砟轨道板。轨道板几何尺寸为4.93 m×2.34 m×0.2 m；CA砂浆层长宽与轨道板相同，厚0.03 m；C40 混凝土支承层宽3 m，厚0.3 m，参数见表1。路基各层参数如图1 所示。地基的竖向取15 m，横向取60 m，线路纵向取1 块长4.93 m 的轨道板，参数见表2。扣件的动刚度为46 N/mm，阻尼系数为23（kN·s）/m。

图1 轨道-路基动力分析模型Fig.1 Dynamic analysis model of track-subgrade

表1 轨道结构计算参数Table 1 Track structure parameters

表2 路基结构计算参数Table 2 Subgrade structure parameters

采用Euler-Bernoulli 梁单元建立钢轨模型。采用3 维8 节点实心立方体缩减积分单元（C3D8R），对路轨垫块、混凝土沥青（CA）砂浆、轨道板及路基进行建模。支承层为C40混凝土，基床表层为级配碎石，采用Abaqus 的“接触对”模拟两者间粗糙接触面关系，其他各结构层之间均采用“绑定”约束。有限元网格划分如图2所示。

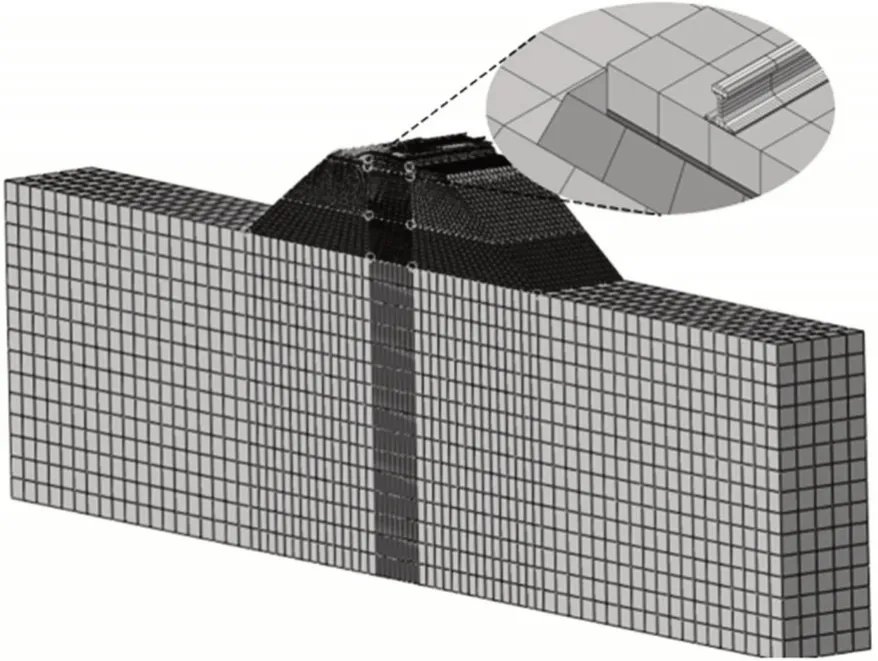
图2 有限元网格划分Fig.2 Finite element meshing

1.2 荷载条件

只考虑竖向荷载作用，忽略车轮与钢轨之间耦合，将轮轨动力简化成一系列竖向荷载，直接施加在钢轨上。列车荷载按照CRH3 型动车组动力车的最大轴重170 kN进行计算。CRH3型动车车厢及车轮的对应位置如图3所示。

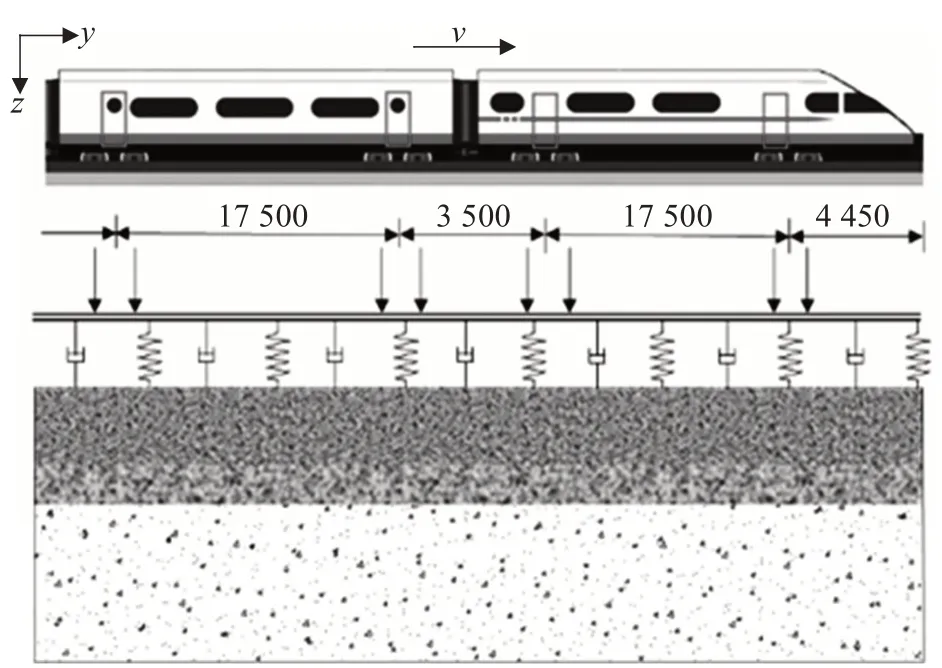
图3 CRH3型动车组车轮分布示意（单位：m）Fig.3 Schematic diagram of wheel distribution of the CRH3 EMU （unit:m）

列车车厢长度和车轮位置固定不变，列车动荷载的模拟应考虑的影响因素有列车轮载、车轮相对位置、行车速度等情况。根据大量理论研究和试验工作，将列车荷载简化成一系列竖向荷载，直接施加于钢轨上。竖向荷载随时间呈周期性变化，列车荷载变化曲线由经验公式模拟[9]，即：

式中：P0、P1、P2、P3分别为与车轮荷载与振动荷载典型值；k1为与车轮个数、间距、车轮荷载的有关系数；k2为钢轨长度方向分散系数。

ωi为振动圆周率，其计算式为：

式中：v为列车行驶速度，取350 km/h（即97.22 m/s）；Li为波长。

式中：m为列车质量，CRH3 型为 750 kg；αi为与路况有关的参数。

竖向荷载的轮轨力为：

式中：t为列车运行时间，s；F（t）为列车荷载，kPa。

激励荷载前0.6 s的时程曲线如图4所示。本研究采用的动力计算时间为2 s。

图4 CRH3型动车组车轮荷载时程曲线Fig.4 Wheel load-time curve of the CRH3 EMU

1.3 边界条件

采用有限元法分析轨道-路基动力问题时，必须从无限介质中划分出1 个有限计算区域。因此，需要设立边界条件模拟能量向无穷远的辐射，采用黏弹性吸波边界[10]，可有效模拟散射波辐射及地基弹性恢复能力。

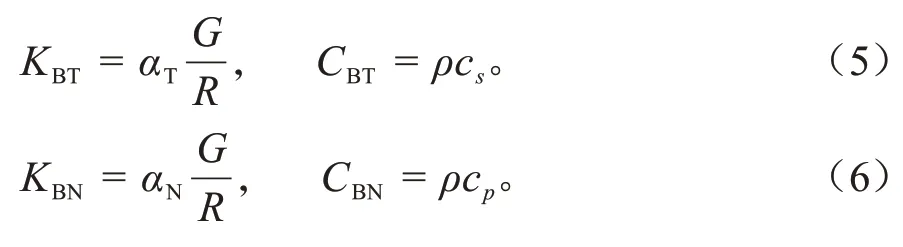
式中：KBT、KBN分别为切向、法向弹簧；CBT、CBN分别为切向、法向阻尼器；α为修正系数；G为剪切模量；R为波源至人工边界点的距离；ρ为质量密度；c为波速。

2 路基动应力特性分析

路基内部各土层动应力水平的发展将直接影响路基稳定性和列车运行安全性，其动力响应主要分析路基内部各点动应力水平及变化状态。

2.1 竖向动应力沿深度衰减

多地现场实测与室内模型试验中路基表面动应力幅值的统计结果见表3。由表3 可知，中国高速铁路路基表面动应力幅值与列车车型、列车行驶速度有关。列车车型相同，路基表面动应力随着列车行驶速度的提升而不断增加。无砟轨道路基表面动应力幅值保持在10～20 kPa。有砟轨道道砟层底面处路基动应力幅值在50～100 kPa，是无砟轨道路的4～5 倍。无砟轨道幅值较小，一般不会造成路基颗粒破碎，但长期累积会产生塑性变形。而有砟轨道容易导致土颗粒破碎，长期会产生较大沉降，因此有砟轨道更需要频繁维护。

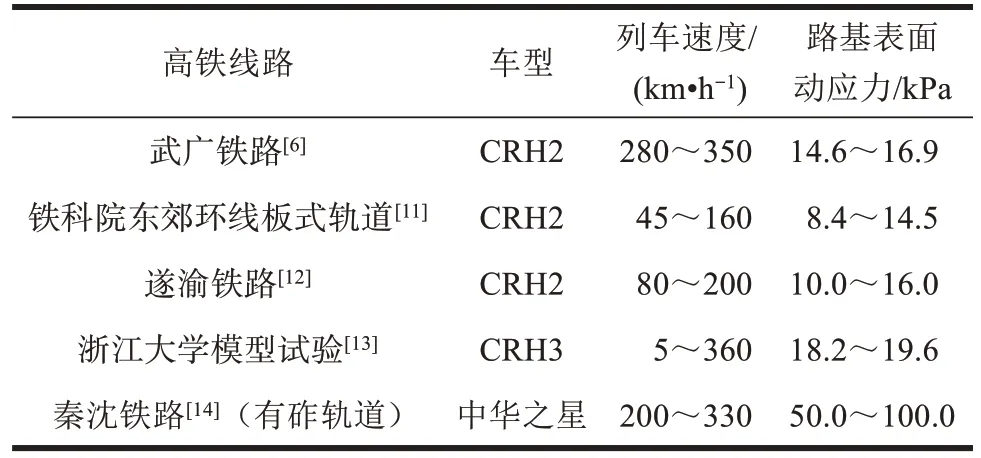
表3 路基表面实测动应力Table 3 Measured dynamic stress on subgrade surface

动应力幅值沿深度变化曲线如图5所示。从图5 中可以看出有限元计算结果中，路基表层顶面（z＝0 m）竖向动应力为17.5 kPa，在地基顶面（z＝4.7 m）竖向动应力为5.32 kPa，动应力幅值随深度的增加总体呈衰减趋势。图5统计了遂渝铁路无砟轨道综合试验段、武广高速综合试验段及浙江大学模型试验中路基表面不同深度下动应力分布。因轨道、车辆及路基实际性状等影响，与同类铁路路基相同位置的动应力幅值存在差异。

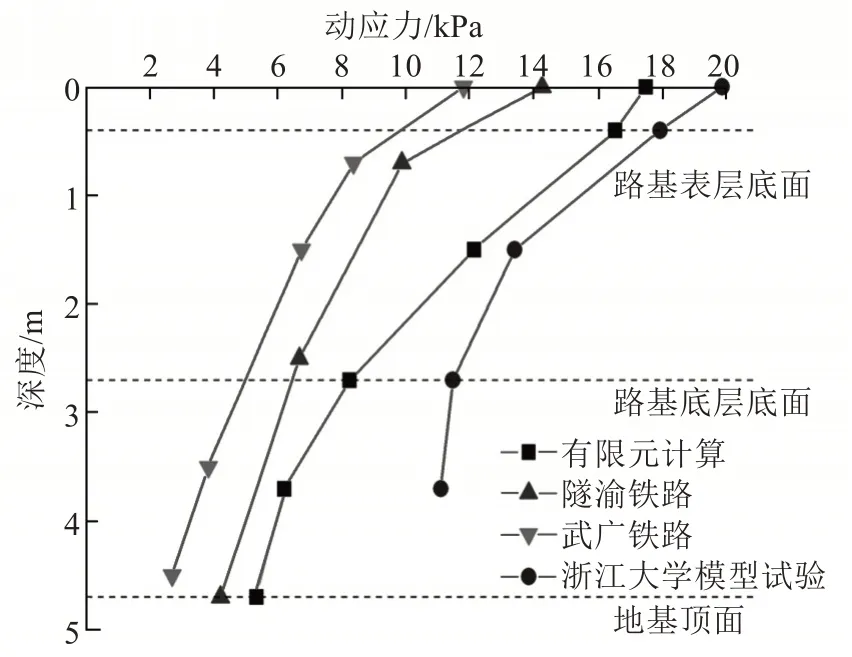
图5 动应力幅值沿深度变化曲线Fig.5 Dynamic stress amplitude-depth curve

从图5 中还可以看出，路基不同位置的动应力水平在基床表层、底层中，有限元计算结果与浙江大学模型试验数据较为接近。在路基底层中线以下及路基本体深度处，本模型计算的动应力水平与浙江大学模型试验结果有较大差别。其原因：①有限元模拟的列车时速为350 km/h，与浙江大学模型试验模拟的列车时速360 km/h 较为接近，在深度1.5 m（混凝土支撑层宽度为3.0 m）范围内的动应力水平较为接近。②由于数值模拟做了一些计算简化，在路基本体处，有限元计算路基动应力经路基能量耗散较多，动应力水平较低。路基动应力衰减系数变化曲线如图6所示，衰减系数计算式为：

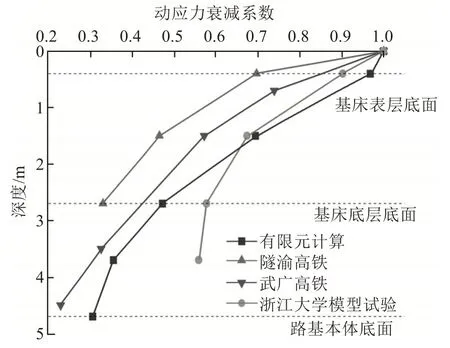
图6 动应力衰减系数变化曲线Fig.6 Change curve of dynamic stress attenuation coefficient

式中：Pz,i深度为im 处竖向动应力幅值；Pz,0为深度为0 m处动应力幅值。

从图6中可以看出，有限元计算结果与线路实测存在差别，有限元计算衰减要慢于线路实测，但最终衰减至0.2～0.3，这是因为有限元计算与线路实测车速有差别，所以导致动应力衰减快慢不同。由于路基结构均为标准路基，最终衰减一致。而模型试验最终只衰减至0.5 左右，其原因是受模型试验边界条件影响，地基结构尺寸较小，振动在地基内引起共振，因此，最终衰减值要高于线路实测值和有限元计算值。

各试验段及有限元计算的衰减系数如图7 所示。从图7中可以看出，武广高速与遂渝高速经过基床表层（0～0.4 m）时，动应力减小为基床表层上表面的70%；在基床底层底面（z＝2.7 m）时，减少至30%～45%；到路基本体底面时，动应力仅为路基顶面的22%。有限元模型值与浙江大学模型试验在基床表层衰减较少，动应力衰减主要发生在基床底层，而遂渝、武广线路实测相同，路基本体内衰减较慢。其原因：①由于基床表层多为级配碎石，对能量耗散较大，故在基床表层衰减较快。②应力扩散叠加效应，路基深层动应力的衰减速率减缓，且同一水平面的应力变得均匀。试验中，遂渝铁路、武广铁路试验段的列车时速较低，而浙大模型试验与有限元计算的列车时速较高，与基床底层基频接近，因此在基床底层内衰减较大。

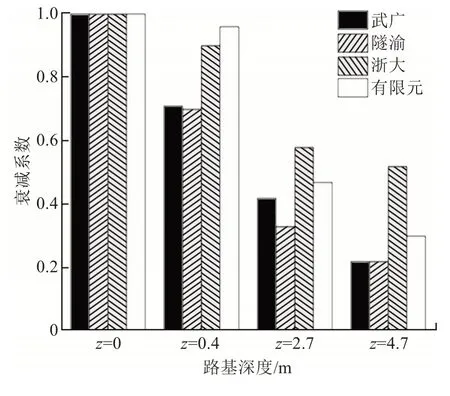
图7 路基衰减系数Fig.7 Subgrade attenuation coefficient histogram

有限元计算路基各处动应力均略高于线路实测数据，地基顶面衰减值较为接近，在z=0.4 、2.7、4.7 m 处，分别为95%、47%、30%，而模型试验最终衰减值较高，是因受模型试验场地限制，地基尺寸既不能与实际工程大小相同，又不能添加黏弹性边界条件，故振动影响较大。

2.2 竖向动应力横向分布特征

路基内不同深度处的竖向动应力幅值沿线路横向变化规律如图8所示。

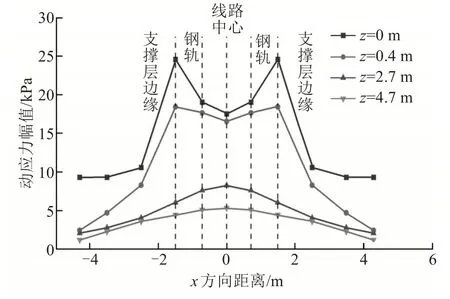
图8 动应力幅值沿横向变化曲线Fig.8 Variation curve of dynamic stress amplitude along the lateral direction

从图8 中可以看出，动应力沿横向分布不均匀，基床表层动土压力沿着水平面分布差异最大。在基床表层顶面（z＝0 m）时，线路中心（x＝0 m）、钢轨下（x＝0.717 5 m）、混凝土支撑层边缘处（x＝1.5 m） 的动土压力依次为 17.5、19.03、24.56 kPa，钢轨下方和支撑层边缘分别比线路中心动应力强度增加了8.74%、40.34%。混凝土支撑层边缘处的基床土体比轨道中心处承担更多的列车荷载，呈现“马鞍形”分布特征。这主要是由于距离荷载作用位置逐渐减小，随着距轨道中心线距离的进一步增加，竖向应力急剧衰减。基床表层底面3个位置的竖向动应力相差较少，分别为16.54、17.63、18.41 kPa，最大相差11.3%。路基本体上、下表面变化不大，而且不再具有“马鞍形”分布特征。线路中心动应力幅值高，x方向距离增加而减少，动应力水平整体较低。

路基竖向动应力幅值在基床表层范围内沿线路横向呈“马鞍形”分布，线路中心与支撑层边缘差值较大，随着路基深度的增加，分布特征逐渐转变为中间高两边低，向线路两侧衰减，总体差值较小。

2.3 竖向动应力纵向分布特征

路基各层竖向动应力沿线路纵向分布特征如图9 所示。路基动应力沿纵向呈“高斯”分布特征，中间高两边低，“中间”为荷载作用位置。

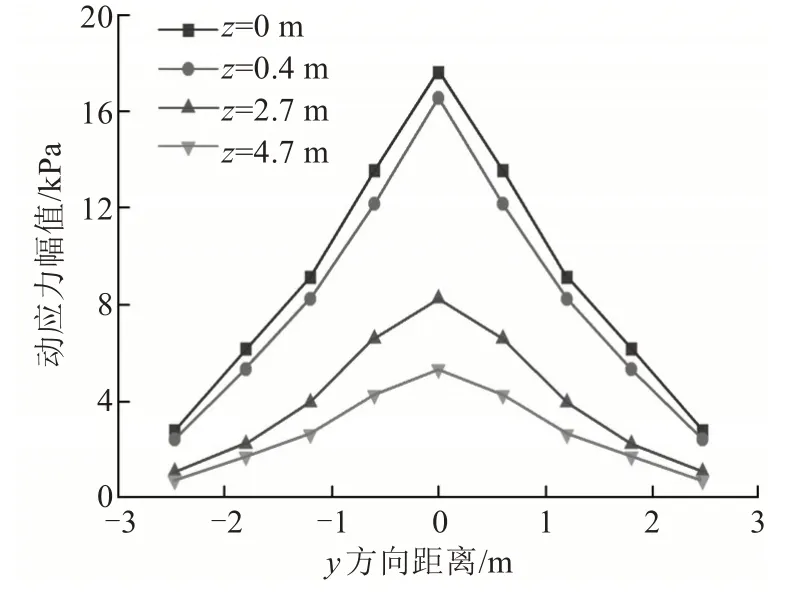
图9 动应力幅值沿纵向变化曲线Fig.9 Variation curve of dynamic stress amplitude along the longitudinal direction

动应力幅值沿y方向衰减见表4。由表4 可知，路基各层竖向动应力幅值沿线路y向衰减一致，轨道板边缘，荷载衰减至轨道半中间的13%～16%。基床表层、底层的差值较大，分别为14.72、14.08 kPa。经路基表层与底层的衰减，路基本体顶面与底面的动应力幅值变小，故横向衰减差值较小，分别为7.15、4.59 kPa。

表4 动应力幅值沿y方向衰减Table 4 Dynamic stress amplitude decays in the y direction

3 分析与讨论

1）利用时域有限元方法分析了列车运行过程中路基沿线路的竖向、横向和纵向的动应力分布特征。从设置合理基床结构满足路基长期动力稳定的角度分析，结合无砟轨道动应力传递特点。表明：①对松软地基、土质路堑和低填方路段，设计时需引起足够重视，并采用合理工程措施达到设计要求。②对于路堤地段，宜改善纵坡，加大填土高度；低填方路段，采用复合地基处理地段增加垫层厚度，并加强水平加固体的强度使动应力不影响地基。③对于浅挖土质路堑或风化成土状的岩石路堑，宜采用优质填料加大换土厚度使基床下伏土层的土质和强度满足基床要求，并加强防排水处理。

2）研究了中国现行CRH3 型动车，轴重170 kN，设计速度为350 km/h，不仅有限元计算分析中部分假设不合理，而且为了简化计算将高速列车移动荷载简化为集中荷载，随时间改变幅值，这些都将会对数值计算结果产生影响。

4 结论

应用Abaqus有限元软件建立了高速（350 km/h）列车、轨道-路基耦合有限元数值模型，模拟了路基和轨道系统上高铁的运行过程，得到结论为：

1）有限元计算路基各处的动应力均略高于线路实测数据，经过路基衰减后较为接近，在z＝0.4、2.7、4.7 m 处衰减值分别为95%、47%、30%，而模型试验最终衰减值较高。这是由于模型试验场地受限制，地基尺寸既不能与实际工程同大，又不能在数值模拟中添加黏弹性边界条件，因此，振动影响较大。

2）路基竖向动应力幅值在基床表层范围内沿线路横向呈“马鞍形”分布，线路中心与支撑层边缘差值较大，随着路基深度增加，分布特征逐渐转变为中间高两边低，向线路两侧衰减，差值较小。

3）路基动应力沿纵向呈“高斯”分布特征，中间高两边低，“中间”为荷载作用位置。路基各层竖向动应力幅值沿线路y向衰减一致，轨道板边缘荷载衰减至轨道半中间的13%～16%。