标准火灾作用后钢管RPC柱的温度场数值模拟★
2022-01-19王英杰闫凤国
王英杰,闫凤国
(陆军工程大学,江苏 南京 210007)
1 概述
为提高工程结构抗火性能,往往采用新材料、新结构等工程措施。钢管混凝土(Conrete Filled Steel Tube,CFST)是由劲性钢筋混凝土和螺旋配筋混凝土发展演变而来的,是约束混凝土的典型代表。由于钢管混凝土中的钢管与核心混凝土之间相互贡献、协同互补、共同工作,使得钢管混凝土具有承载力高、刚度大、塑性和韧性好、耐火性能好、便于施工和经济效益好等优点(钟善铜[1]、蔡绍怀[2]、韩林海[3])。现代钢管混凝土既是一种高强高性能结构材料,又是一种高效施工技术,它最适用于大跨、高层、重载和抗震抗爆结构的受压杆件(蔡绍怀)。随着CFST柱在实际工程中的应用日益增多,其抗火性能成为近年来研究者关注的热点问题之一。CFST柱良好的耐火性能,不仅体现在火灾作用下构件具有良好的抗火性能,而且火灾作用后构件还具有较好的可修复性能(韩林海)。由于钢管及其核心混凝土的协同互补,CFST柱在经历火灾高温后,其核心混凝土不会出现钢筋混凝土柱中的“爆裂”和剥落现象,钢管也不会出现钢结构中的失稳和扭曲现象。火灾后CFST柱的整体性良好,便于修复加固后继续使用。
韩林海及其课题组采用实验和数值分析等手段研究了CFST柱在恒高温和标准火灾升温作用后的力学性能和残余承载力变化规律,提出了火灾后CFST柱残余承载力和变形的实用计算方法。李毅等[4]采用有限元分析方法也提出了火灾后CFST轴压短柱残余承载力的简化计算公式。Tao等[5]对火灾作用后钢管中钢和混凝土的界面性能进行试验,研究了受火时间、试件长度、界面形状等因素对黏结性能的影响。张春亮[6]根据13根高温后钢管混凝土的推出试验,提出了黏结强度计算公式。韩林海等[7]提出了钢-混组合结构抗火设计原理,包括火灾后结构的力学性能和加固措施评估方法,为损伤评估和修复加固提供了理论基础。韩林海[8]对火灾后CFST柱分别采用“增大截面法”和“FRP包裹法”对加固后的静力、滞回性能进行了研究,定量分析了加固后CFST构件力学性能的变化规律。
火灾后钢管RPC柱力学性能的降低主要表现为强度下降和刚度减小两个方面。强度的下降将直接导致结构构件承载力的降低,刚度的减小则会减弱结构抵抗变形的能力,并可能引起结构内力的重分布。现有文献中关于火灾后CFST柱残余力学性能的计算方法主要包括有限元方法和简化计算方法两种。有限元方法先获得构件截面最高温度分布,采用高温后钢材和混凝土力学性能指标以及应力-应变本构模型,按实际尺寸采用数值分析程序进行计算;简化计算方法先根据截面温度场分布将火灾后构件截面等效为均质截面或若干条带,再采用常温下的计算方法计算CFST柱的残余力学性能。由于火灾的影响因素众多,不确定性和随机性大,本文通过归纳分析高温后钢材和RPC的高温热工性能,利用有限元软件ANSYS13.0分析ISO-834标准火灾作用后钢管RPC柱横截面温度场分布规律,为残余力学性能的分析计算奠定基础。
2 材料的高温热工性能
在温度场分析中涉及的材料热工性能参数只有导热系数、质量热熔(比热容)和质量密度三项,其他热工参数都可由这三个参数导出。这些参数因材料的组成不同而不同,而且还随温度的升高呈非线性的变化。此外,材料的线膨胀系数也是结构抗火分析中的重要参数,它只影响材料和结构的温度变形和应力,而与温度场分析无关。
2.1 钢材的高温热工性能
钢材的高温热工性能研究相对成熟,其热工参数已有较多的定量成果,韩林海等采用Lie[9]建议的钢材热工参数对CFST柱进行温度场模拟取得了良好的效果。其中,导热系数的表达式为:
(1)
比热容的表达式为:
(2)
线膨胀系数的表达式为:
(3)
本文对钢管RPC柱温度场进行有限元分析时,钢材热工参数取值如表1所示。
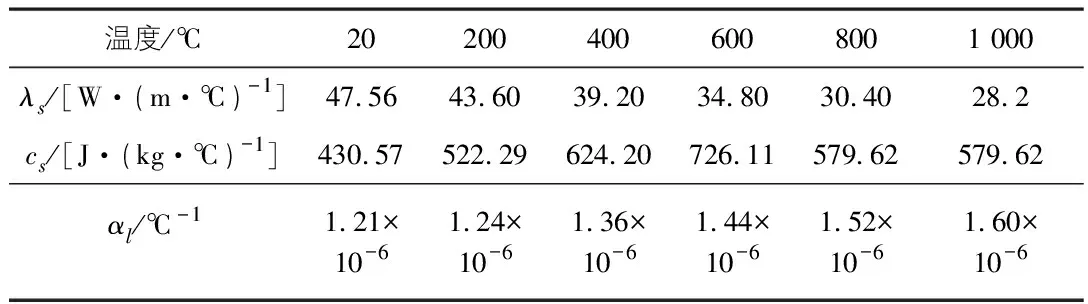
表1 钢材热工参数取值
2.2 RPC的高温热工性能
2.2.1 导热系数λc
影响混凝土导热系数的主要因素有:材料的配合比、骨料类型、含水量、龄期以及施工工艺等,其中骨料的矿物学特性对导热系数影响较大,不同类型骨料的混凝土导热系数会相差较大。目前针对RPC导热系数的试验研究还相对较少,表2给出了部分学者建议的普通混凝土和RPC导热系数表达式。图1为普通混凝土、RPC导热系数随温度变化曲线。

表2 混凝土的导热系数
由图1可知,硅质骨料混凝土的导热系数较钙质骨料的导热系数稍高,RPC主要为硅质骨料且内部结构致密,常温下RPC导热系数达到普通混凝土的两倍。随着温度的升高RPC导热系数迅速下降,温度大于300 ℃后RPC导热系数下降幅度变缓,至800 ℃后逐渐趋于平稳。本文采用郑文忠建议的RPC导热系数值如表3所示。
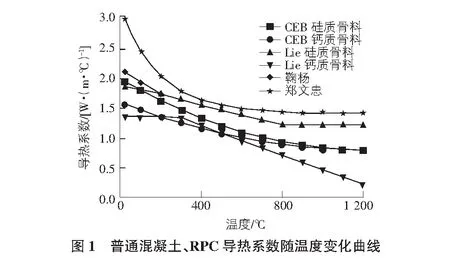

表3 RPC导热系数取值
2.2.2 比热容cc和质量密度ρc
混凝土的比热容主要受温度、骨料类型、配合比和含水量的影响,但这些因素对比热容的影响不大,一般文献给出的公式中均不考虑它们的影响。表4给出了部分学者建议的普通混凝土和RPC比热容表达式。图2为混凝土的比热容随温度变化曲线。

表4 混凝土的比热容

由图2可知,RPC的比热容大于普通混凝土比热容。郑文忠等对RPC的比热容进行有限元分析和计算,认为钢纤维掺量对活性粉末混凝土比热容值影响不大,本文采用郑文忠建议的RPC比热容值如表5所示。

表5 RPC比热容取值
2.2.3 热膨胀系数αi
影响混凝土材料热膨胀系数的因素较多,目前针对RPC热膨胀系数的试验仅在250 ℃以内,而普通混凝土的试验表明超过800 ℃以后近似常数[13],为简化计算本文采用Lie给出的仅考虑温度影响的热膨胀系数表达式:
αc=(6+0.008T)×10-6
(4)
3 构件截面的温度场模拟
3.1 标准火灾曲线
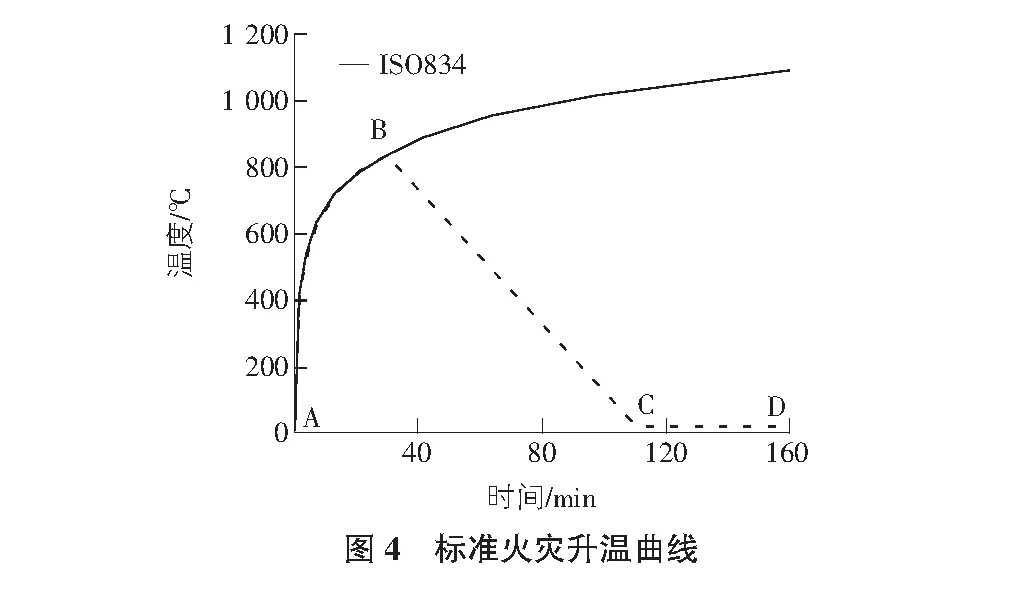
火灾对结构的最直接作用是表面加热,因而确定火灾场景是结构抗火分析最基本、最重要的条件。图3为室内火灾的典型发展过程包括:初期增长阶段、全盛阶段和衰退阶段。有鉴于建筑物实际火灾的复杂性和随机性,一些经验模型仍具有较大的随机性,为便于开展结构抗火试验及抗火要求,许多国家的有关研究机构和学术组织相继制定了标准的火灾温度-时间曲线。国际标准化组织(ISO)推荐的一种建筑构件抗火试验曲线最为常用,其温度时间曲线如图4所示。

图4中各阶段的数学表达式如下:
1)升温段(A→B)。
T=T0+345lg(8t+1)
(5)
2)降温段(B→C)。
(6)
3)常温段(B→D)。
T=T0
(7)
其中,T为温度;t为火灾作用时间;th为升温时间;Th为升温最高温度;T0为室温,常取值为20 ℃。
3.2 温度场的有限元模型
有限元软件ANSYS包括了热传导问题的数值分析,方便结构温度场的分析计算。考虑到火灾时对结构温度变化影响因素众多,且变异性较大,因此为简化分析过程,在满足工程精度要求的前提下使温度场的分析更为简单、实用,做以下假设:1)温度场在沿柱的长度方向不变,那么可将钢管RPC柱的温度场问题转化为二维问题来进行分析。2)钢材和RPC的热工性能是均匀且各向同性的。3)忽略 钢管与RPC之间的接触热阻,假设完全传热。4)构件内部无热生成,忽略RPC中水分迁移对温度场的影响。
此外,韩林海的研究表明在考虑升温和降温全过程时内部混凝土的最高温度不同,在采用最高温度时仅考虑升温过程也是可以接受的。
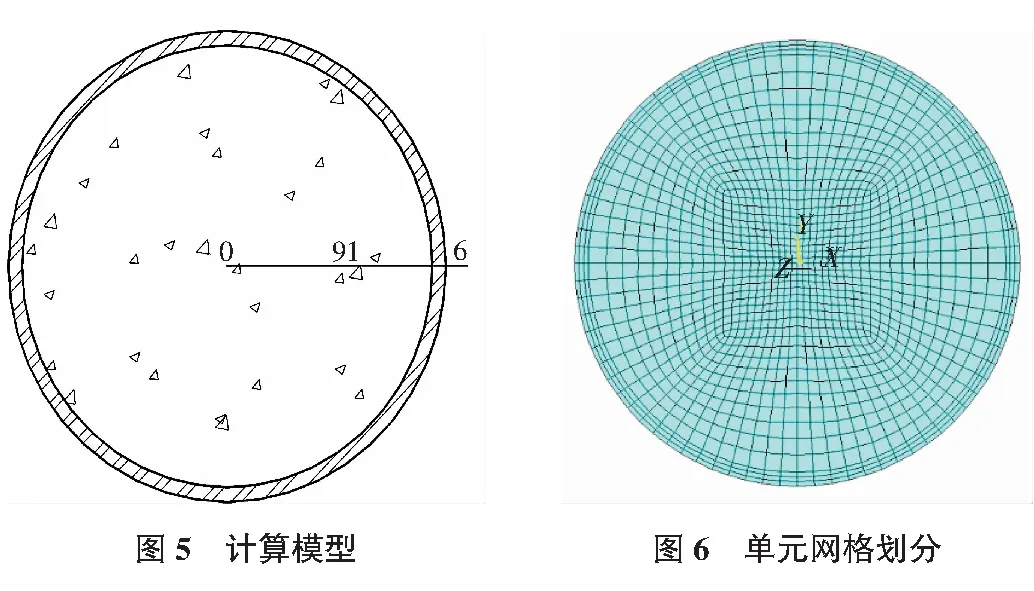
3.2.1 温度场计算模型的建立
温度场计算的几何模型如图5所示。采用有限元分析软件ANSYS13.0建模,钢材和RPC材料均采用四节点平面热单元PLANE55,几何模型如网络划分采用映射网络划分,划分后的截面如图6所示。钢管和RPC之间设为完全接触。
3.2.2 加载与求解
分析的初始温度取为20 ℃,温度荷载按ISO-834标准升温曲线施加在钢管外表面。总加载时间分别设为30 min,60 min,90 min,105 min,120 min和150 min六种工况,求解的时间步长均选择固定时间1 min。ANSYS分析温度场时采用有限元分析方法求解,通过处理后可以得到温度场分布不同点的温度时间曲线等数据。
4 温度场计算结果分析
4.1 不同受火时间的温度场分布
图7为火灾升温时间为30 min,60 min, 90 min,105 min,120 min和150 min时柱横截面的温度场云图。从图7中可以看出,在不同受火时间下,外层钢管温度均可认为均匀分布。而RPC为热惰性材料,靠近钢管附近的温度最高,温度逐渐向内部传递,形成明显的不均匀温度场;靠近钢管附近的温度场梯度也最大,自外向内逐渐减小;随着受火时间的增加,RPC温度不断升高,温度梯度逐渐减小,趋于均匀分布。受火时间为90 min时,核心混凝土中心温度超过了600 ℃;受火时间为150 min时,核心RPC中心温度超过800 ℃。
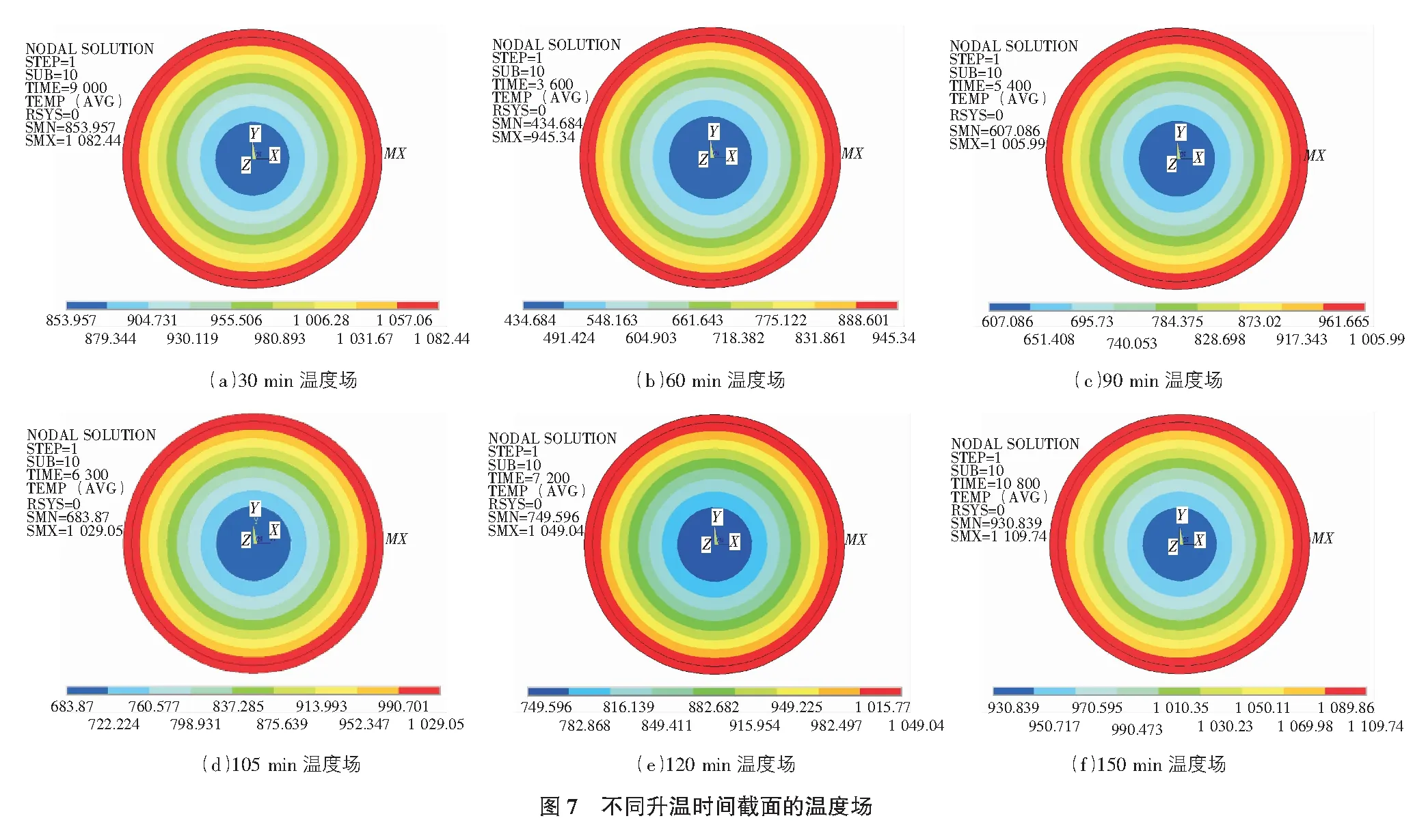
4.2 不同点温度随时间的变化
图8(a)为不同受火时间下核心RPC沿径向不同点的温度变化曲线,图8(b)为截面不同点的温度时间曲线。其中d为截面内点距柱横截面中心的距离。钢管外边缘的点由于施加的是标准升温曲线,故其温度时间曲线与标准升温曲线一致。越靠近核心区域的点,升温曲线越平缓,中心点的温度时间曲线接近直线。


4.3 温度场的简化计算
在进行火灾后钢管RPC柱力学性能的简化计算时,钢管可认为温度均匀分布,取外表面和内表面温度的平均值即可。RPC需要将截面划分为若干条带,根据温度场的云图可知,可根据曲线的特征采用指数函数形式拟合:
(8)
其中,Tc为RPC各点的温度;T0,A,B均为待定系数,
不同受火时间的取值如表6所示。

表6 参数取值
5 结论
本文通过分析RPC材料特性,合理选择了钢材和RPC的高温热工参数,采用ANSYS软件分析了钢管RPC柱在ISO-834标准火灾升温后的截面温度场,并提出了简化计算方法,得到以下结论:
1)在不同受火时间下,外层钢管温度均可认为均匀分布,而RPC形成明显的不均匀温度场,靠近钢管附近的温度最高,温度逐渐向内部传递;靠近钢管附近的温度场梯度也最大,自外向内逐渐减小。
2)随着受火时间的增加,RPC温度不断升高,温度梯度逐渐减小,趋于均匀分布;越靠近核心区域的点,升温曲线越平缓,中心点的温度时间曲线接近直线。
3)在简化计算时,钢管可认为温度均匀分度,取外表面和内表面温度的平均值即可;RPC需要将截面划分为若干条带,采用指数函数形式公式进行计算。
