高钢级天然气管道站场三通孔锥形坡口优化分析

高 琦，牛海仲，赵 斌，杨 明， 尤泽广

（1.国家管网集团 西部管道有限责任公司，新疆 乌鲁木齐 830011；2.中国石油天然气管道工程有限公司，河北 廊坊 065000；3.中国石油管道局工程有限公司 燃气分公司，河北 廊坊 065000）

近年来天然气站场使用的高压力、大口径工艺管道日益增多，连接工艺管道的三通规格也随之增大。三通结构通过增大主管管壁的厚度对支管开孔削弱的面积进行补强，因此三通的壁厚远大于与之连接的工艺管道壁厚。目前工程上三通与工艺管道焊接的壁厚差最大可达40 mm，焊接质量因此控制难度大，易产生初始焊接缺陷和应力集中，成为站场三通环焊缝失效问题的主要原因之一。对此，文中基于文献调研，提出了一种孔锥形式的新型坡口，展开坡口参数优化和承压能力校核研究，确定了最优孔锥形坡口形式和尺寸。

1 三通技术现状研究

三通焊接结构的研究主要是尺寸与安全性能的研究。Goodall等[1]分析了开孔设备（三通、大小头）等在内压作用下的应力分布。薛丽萍等[2]对三通进行了试验分析及弹塑性有限元分析，验证了有限元分析的可靠性。沈伟、轩福贞、刘彩霞、梁银林等[3-6]研究了不同载荷下无缺陷及含缺陷的焊制三通的失效形式。轩福贞等[7-8]运用有限元方法分析了等径和异径挤压三通的应力分布规律。刘张羽等[9]运用有限元方法研究了不同过渡方式三通的失效形式与优化设计。王旗华等[10]提出了三通焊前坡口切割的新理论依据与思路。尤泽广、王瑞瑞等[11-12]运用有限元结合极限分析设计方法，分析了三通结构形式对应力集中的影响，确定了中俄东线站场低温环境用直径1 422 mm×1 219 mm三通尺寸、材料性能等重要因素。这些研究多是针对三通整体结构的极限校核，未针对孔锥形坡口结构尺寸与应力集中进行分析。

2 三通孔锥形坡口建模

2.1 三通结构尺寸

某天然气站场连接工艺管道的三通结构见图1。

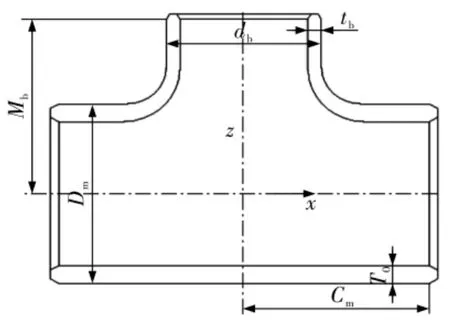
图1 三通结构尺寸示图

图1中，主管外径Dm=1 422 mm、支管外径db=1 219 mm、主管壁厚T0=57 mm，支管壁厚tb=48 mm、主管管口端面到支管中心线的距离Cm=1 060 mm、支管管口端面到主管中心的距离Mb=1 090 mm。

2.2 孔锥形坡口结构

在三通主管/支管边缘内部切割一定的锥孔长度，实现三通与工艺管道的等内径连接，此连接形成的孔锥形坡口结构见图2。图2中，θ为坡口角度，h为坡口深度，t为三通管道短节厚度。三通主管、支管皆采用孔锥形坡口与工艺管道连接。

图2 三通与工艺管道焊接坡口结构示图

2.3 三通材料及结构参数

三通材料 X80，材料密度 ρ=7 850 kg/m3，线弹性阶段弹性模量 E=2.1×105MPa，泊松比μ=0.3，屈服强度581 MPa,拉伸强度625 MPa。建模所用三通焊接坡口参数化尺寸设置见表1。

表1 三通参数化尺寸设置

2.4 三通组合件模型与网格

对由三通主体、主管短节、支管短节、主管封头、支管封头组成的三通组合件建模。根据三通组合件的结构对称特点，建立1/4简化模型，见图3。运用六面体网格对模型进行划分，网格整体控制采用Curvature计算方法，网格过度系数设置为1.1，对内部构件表面进行局部细化处理，共划分出节点3 753 739个、网格955 340个。网格平均单元质量0.829 45，偏斜0.255 14，网格纵横比2.945 123，整体单元质量评价为高，满足计算要求。

图3 三通组合件1/4简化网格模型

2.5 应力集中点位标识

对易发生应力集中的三通组合件部位和区域进行标识。A、B、C依次表示坡口与工艺管道连接位置、孔锥内切顶点位置、焊缝与短节连接位置，字母前带数字1表示应力集中位置在主管上，字母前带数字2表示应力集中位置在支管上。三通组合件应力集中点位置示意图见图4。

图4 三通组合件应力集中点位置示图

2.6 模型边界条件设定

在三通组合件对称截面施加关于x方向对称的位移边界条件和关于z方向对称位移边界条件，见图5。

图5 三通组合件位移边界条件

按照设计压力12 MPa，在三通组合件内壁施加均布内压，方向垂直壁面，并考虑结构大变形特性，施加的力边界条件见图6。

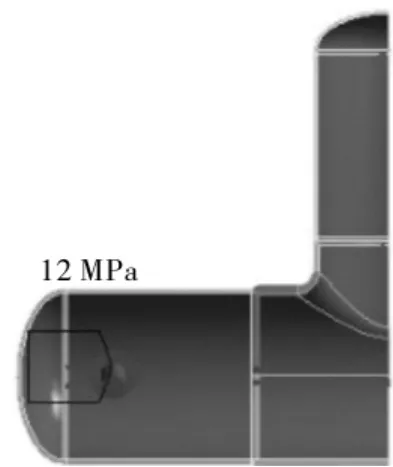
图6 三通组合件力边界条件

3 三通锥孔形坡口结构参数优化

3.1 总体结构参数敏感性

运用有限元软件ANSYS Workbench进行响应曲面优化分析。以主管短节厚度t0、主管坡口深度h0、主管坡口角度θ0、支管坡口深度h1、支管坡口角度 θ1为优化参数，以 1A、1B、1C、2A、2B、2C 位置最大Mises应力为目标函数，采用随机抽样法[13-15]，在表1参数范围内构造27组试验点进行参数敏感性分析。支管坡口深度和坡口角度对主管应力影响很小，其他尺寸参数对主管应力影响计算结果见图7，尺寸参数对支管应力影响计算结果见图8。

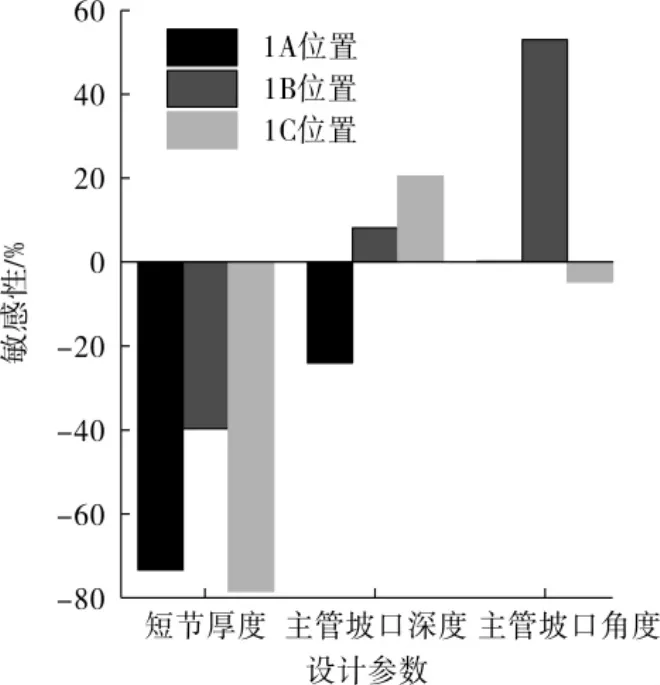
图7 尺寸参数对主管应力敏感性分析图

图8 尺寸参数对支管应力敏感性分析图

综合图7和图8可以知道，t0对主管坡口的最大Mises应力影响较大，为负相关；h与A位置最大 Mises应力负相关，与 B、C位置最大Mises应力正相关；θ与C位置最大Mises应力负相关，与B位置最大Mises应力正相关。 t0与θ0对主管应力集中影响显著，h1与θ1对支管应力集中影响显著。

3.2 主管参数优化

3.2.1 主管短节厚度t0

主管上不同危险点最大Mises应力随t0变化的关系曲线见图9。

图9 主管上不同危险点最大Mises应力随t0变化曲线

由图9可知，1A、1B、1C位置最大Mises应力均随 t0增大而减小，t0由 30.8 mm增大到 45 mm时，1A、1B、1C位置最大 Mises应力增幅分别为-52 MPa、-109 MPa，-104 MPa。1A 位置、1B 位置应力曲线可近似看作线性曲线，运用线性回归方法求得1A位置应力曲线降频为3.9 MPa/mm，1B位置应力曲线降频为7.7 MPa/mm。当t0＜42 mm时，1C位置应力曲线亦呈线性变化，运用线性回归方法求得1C位置应力曲线降频为9.1 MPa/mm，当 t0≥42 mm后最大 Mises应力对 t0的变化不再敏感。

3.2.2 主管坡口深度h0

主管上不同危险点最大Mises应力随h0变化的关系曲线见图10。

图10 主管上不同危险点最大Mises应力随h0变化曲线

由图10可知，h0由 10 mm增大到50 mm时，1A、1B、1C位置的最大 Mises应力增幅分别为-15 MPa、19 MPa、28 MPa。 1A位置最大应力随 h0增大而降低，当h0＜35 mm时，1A位置应力曲线呈线性下降，运用线性回归方法求得降频为0.67 MPa/mm，当 h0≥35 mm后最大 Mises应力对h0变化不再敏感。1B处最大应力随h0增大而近似增大，当h0＜35 mm，1B位置应力曲线呈线性增加，运用线性回归方法求得增频为0.84 MPa/mm，当h0≥35 mm后最大的Mises应力对h0变化不再敏感。1C位置最大应力随h0增大呈线性增大，运用线性回归方法求得增频为0.74 MPa/mm。

3.2.3 主管坡口角度θ0

主管上不同危险点最大Mises应力随θ0变化的关系曲线见图11。

图11 主管上不同危险点最大Mises应力随θ0变化曲线

由图11可以知道，θ0由14°增大到40°时，1A、1B、1C位置的最大 Mises应力增幅分别为0.02 MPa、145 MPa、-6.6 MPa。由图 11 还可知，随着θ0的增加，1A位置最大应力增大很小，1B位置最大应力呈近似线性增加，运用线性回归方法求得增频为5.7 MPa/mm。1C位置最大应力曲线呈近似线性减小，运用线性回归方法求得降频为0.23 MPa/mm。

3.3 支管参数优化

3.3.1 支管坡口深度h1

支管上不同应力危险点最大Mises应力随h1变化的关系曲线见图12。

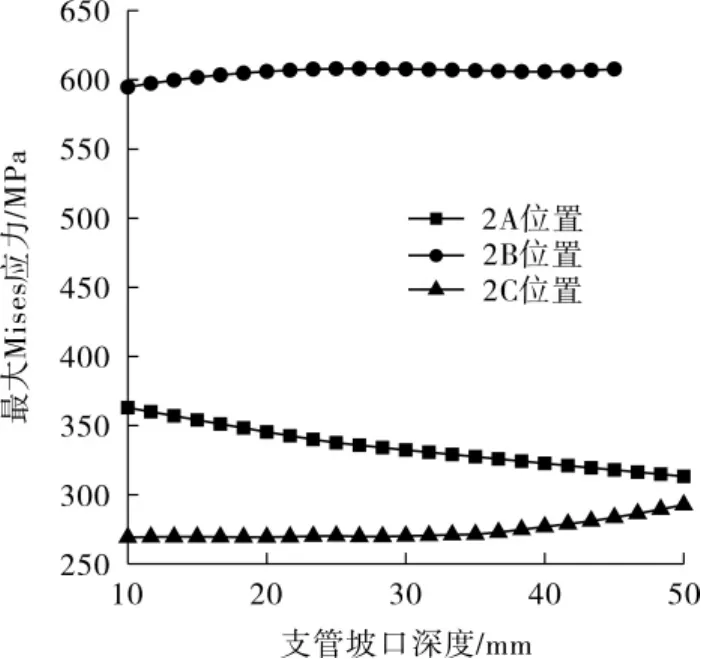
图12 支管上不同危险点最大Mises应力随h1变化曲线

由图12可以知道，h1由10 mm增大到50 mm时，2A、2B、2C位置最大 Mises应力增幅分别为-50 MPa、16 MPa、23 MPa。由图 12 还可知，随着 h1的增大，2A位置最大应力曲线线性减小，运用线性回归方法求得降频为1.2 MPa/mm。2B位置最大应力在h1＜20 mm区间线性增加，运用线性回归方法求得增频为 1.1 MPa/mm，当 h1≥20 mm后最大的Mises应力对h1变化不再敏感。2C位置最大应力曲线在 h1＜35 mm时对 h1变化不敏感，在35 mm＜h1＜50 mm时线性增加，运用线性回归方法求得增频为1.2 MPa/mm。

3.3.2 支管坡口角度θ1

支管上不同应力危险点最大Mises应力随θ1变化的关系曲线见图13。

图13 支管上不同危险点最大Mises应力随θ1变化曲线

由图 13可以知道，θ1由 14°增大到 40°时，2A、2B、2C位置相应的 Mises应力增幅分别为9.6 MPa、184 MPa、-5.6 MPa。 由图 13 还可知，2A位置最大应力随θ1线性增大，运用线性回归方法求得增频为0.87 MPa/mm。2B位置最大应力随θ1近线性增加，运用线性回归方法求得增频为7.3 MPa/mm。2C位置最大应力随θ1线性减小，运用线性回归方法求得降频为0.2 MPa/mm。

3.4 优化结果综合分析

综合分析三通组合件主管和支管参数的优化结果可知，三通连接工艺管道的坡口深度h对坡口短接连接位置A、焊缝短节连接位置C的最大Mises应力变化影响较大，对孔锥内切顶点位置B的最大应力变化影响较小。当h＜35mm时，位置A最大应力降低较快，位置C最大应力增加缓慢；当 h＞35mm，位置A最大应力降低不显著，位置 C最大应力增大加快。三通连接工艺管道的坡口角度θ对孔锥内切顶点位置B的最大应力变化影响很大，对焊缝短节连接位置C的最大应力变化影响较大，对坡口与短接连接位置A的最大应力变化影响很小。随着θ的增大，位置1B、2 B的最大应力增大较多，位置1C、2C的最大应力减小。

4 坡口深度与承压能力计算分析

4.1 模型参数与边界设置

运用有限元数值模拟方法分析孔锥形坡口深度对三通组合件极限承压能力的影响。基于初始几何模型，通过修改模型参数，构造7个坡口深度不同、相接短节厚度30.8 mm、主管坡口角度30°、支管坡口角度30°、支管厚度27.5 mm的三通组合件模型。运用六面体网格，采用整体控制加局部优化方式对各模型进行划分。对三通组合件模型施加的位移边界不变，在三通组合件内壁施加均布内压，方向垂直壁面，设置极限压强为100 MPa，并考虑结构大变形特性。三通组合件模型坡口深度及网格划分结果见表2。

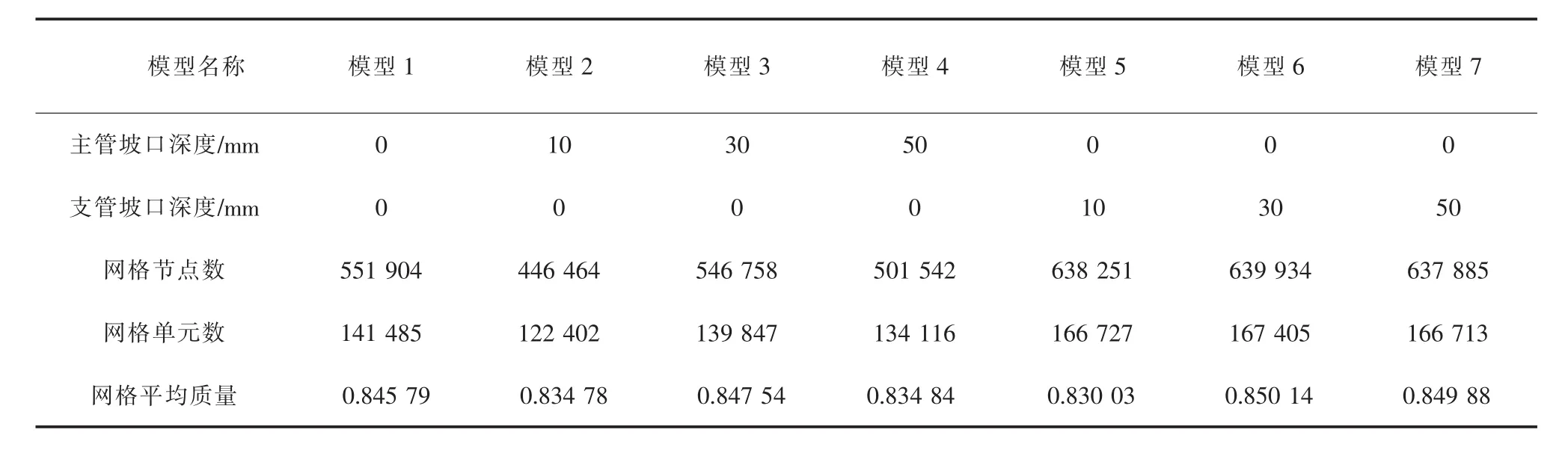
表2 三通组合件模型坡口深度与网格划分结果

4.2 模拟结果与分析

三通组合件模型1～模型7在极限载荷下的应力分布见图14～图20，极限载荷及对应的最大应力见表3。

图14 模型1极限载荷应力分布

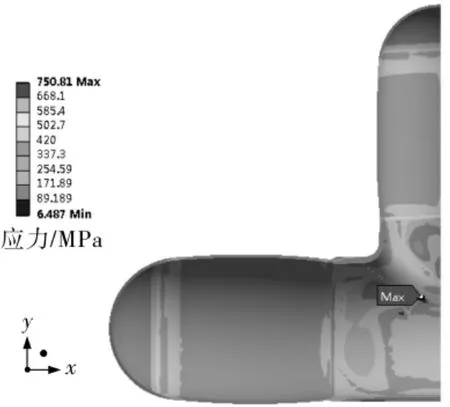
图15 模型2极限载荷应力分布

图16 模型3极限载荷应力分布

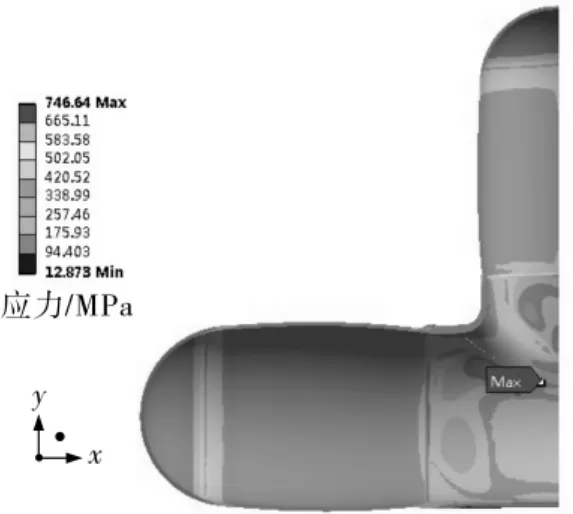
图17 模型4极限载荷应力分布

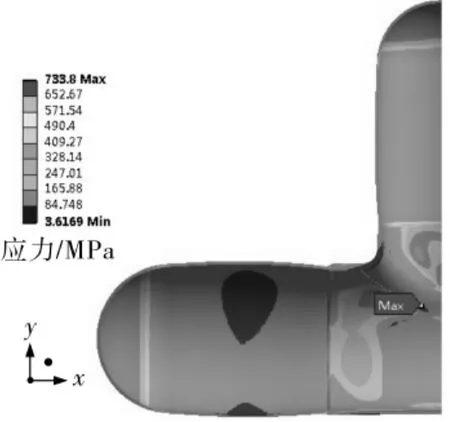
图18 模型5极限载荷应力分布

图19 模型6极限载荷应力分布

图20 模型7极限载荷应力分布

表3 三通组合件模型极限载荷与最大应力

由图14～图20和表3可知，坡口深度不同的三通组合件具有相似的应力分布规律，三通本体的应力最大，封头的应力最小，最大应力点都在三通腹部内表面。模型 1、模型5、模型6、模型 7的三通肩部与支管应力分布也接近最大应力。模型1的极限承压能力最大，模型7的最小，两者差为2.227 MPa。三通组合件在极限载荷下结构最大应力位于三通腹部内表面尖角处，孔锥形坡口位于主管的组合件在极限载荷下最大应力值大于其他模型，结构极限承压能力随着坡口深度的增大而降低，但不同坡口深度的三通组合件极限承压值相差较小。

5 结语

孔锥形坡口降低了三通承压能力，支管孔锥形坡口对三通承压能力的影响大于主管。针对直径1 42 2mm×1 219 mm的X80孔锥形坡口三通组合件，增加相接短节厚度t0可降低连接坡口位置应力集中。t0增至42 mm时，最大应力趋于稳定。增加坡口深度h可降低坡口内表面应力集中。h增至35 mm时，坡口内表面最大应力趋于稳定。减小坡口角度θ可减小焊缝根部的应力集中。