双明模耦合的双波段类电磁诱导透明研究*

宁仁霞 黄旺 王菲 孙剑 焦铮

1)(黄山学院信息工程学院,黄山 245041)

2)(南京航空航天大学,雷达成像与微波光子技术教育部重点实验室,南京 211106)

3)(智能微系统安徽省工程技术研究中心,黄山 245041)

本文设计了一种双层开口方环和双C 型结构的超材料结构,在太赫兹波段具有双波段的类电磁诱导透明效应.该结构在1.438 THz 和1.699 THz 处出现透射峰.通过电磁场分布分析讨论产生双频带电磁诱导透明的原因,利用等效电路分析方法进一步解释了超材料中的类电磁诱导透明效应.研究了超材料开口方环的开口大小和双C 型结构距离以及改变入射角度时对透射窗口的影响,结果发现在改变入射角度时,所设计材料透射谱线变化较大,表现出对角度的高敏感性.同时,改变环境的介电常数可以得到该结构的透射谱产生明显的红移.以上研究结果表明该结构在角度滤波器,折射率传感器等器件中有潜在的应用.

1 引言

近几十年来,人们在人工电磁材料(也称为超材料,metamaterials)领域开展了大量的研究[1-3].这主要是因为超材料具有非自然的电磁特性和物理特性,如负折射率、完美吸收[4]、电磁波隐身和电磁诱导透明(electromagnetically induced transparency,EIT)[5,6].EIT 效应是由多路激发引起,干涉效应所导致的,使介质对入射的电磁波透明而引起的一种量子现象[7].这种现象最早在原子系统里被发现.然而,在最初研究的三原子系统中想要实现EIT 现象需要严格的实验条件,如较高强度泵浦源和合适的原子能级系统以及较低的温度,因此极大地限制了其性能应用和进一步的研究[8].近年来,人们在热原子系统[9]、电路系统、超材料等中发现了类EIT 效应[10],尤其是在超材料中发现类EIT 以来,它一直受到广泛关注,例如非线性器件、光存储、以及传感器等领域有潜在的应用[11-13].

与原子系统里实现的EIT 效应所不同的是无需非常苛刻的实验条件就可以在超材料中实现EIT 效应[10,14].研究者在设计超材料结构时通常是通过改变上层金属结构或者材料[15-20],从而得到相应的明模式或者暗模式.一般情况下明模式的辐射损耗较大,故Q值会较低而暗模式的辐射损耗较小故Q值会较高,当明模与暗模耦合时,在谐振点附近就会产生较为尖锐的透射峰[21-24].

本文主要研究了在太赫兹波段下的双明模耦合结构的类EIT 效应,对所设计结构的参数进行分析,结合电场和磁场分布,解释了该EIT 效应是通过双明模结构进行耦合的物理机制.通过研究入射角和背景环境的介电常数,发现该结构对入射电磁波角度敏感,同时具有折射率传感特性.该结果在太赫兹角度开关、折射率传感等方面有潜在的应用.

2 单元结构设计

如图1 所示,基本单元结构为双层结构,顶层为金属层,基板为二氧化硅.本单元为p×p的周期单元,结构单元参数如下:p=150 µm,基板厚度d=20 µm,基板的介电常数ε=3.75.上层金属由一个双C 结构和一个开口方环耦合而成,金属的电导率为σ=5.8×107S/m,金属的双C 的外宽为120 µm,内宽为110 µm,金属的开口方环的外宽为74 µm,内宽为64 µm,金属层厚度为5 µm,外部金属双C 开口的大小和内部金属开口方环的水平开口的大小,垂直开口大小都为4 µm.本设计采用时域有限差分法(finite difference time domain,FDTD)对透射率进行计算.其中,金属层的几何参数为L1=120 µm,L2=110 µm,L3=74 µm,L4=64 µm,t=5 µm,g=4µm,g1=4 µm,g2=4 µm,a=16 µm,b=14 µm,边界条件在x方向和y方向上设置的是周期性边界条件,在z方向上设置的是开放性边界条件,入射电磁波为横电波模式(transverse wave,TE mode),入射角为θ.

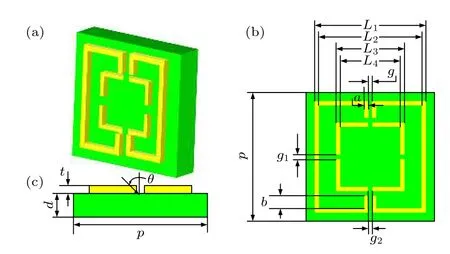
图1 双明模耦合的单元结构图 (a)由顶层金属层和底层非金属层构成的超材料结构的三维视图;(b)所设计超材料结构的正视图;(c)所设计超材料的侧视图Fig.1.Unit structure diagram of bright-bright mode coupling:(a)3D view of metamaterial structure consisting of top metal layer and bottom nonmetal layer;(b)view of the designed metamaterial structure;(c)side view of the designed metamaterial structure.

3 计算结果与讨论

为分析本文设计的 EIT 超材料结构在太赫兹波段对入射电磁波的响应情况及产生机理,对结构图所示的完整结构去掉最外层的双C 结构只保留内部开口方环即结构Ⅰ,去掉内部方环仅保留最外层双C 结构即结构Ⅱ,分别对这3 种结构在入射电磁波垂直入射情况下进行计算分析得到透射率随频率变化的情况,如图2 中结构Ⅰ所示.红色线表示的是开口方环结构的透射谱,其透射峰在1.531 THz处,透射谷分别在1.509 THz 和1.603 THz处,根据图3(b)中各谐振点的电场分布可以看出中即在透射谷点产生了谐振,此时,在TE 模式下,开口方环的产生了类EIT 现象,从电场分布来看,在低频透射谷的电场主要集中在方环开口处,此时开口环可以等效为LC 谐振回路,开口处等效为电容,方环等效为电感,此时水平开口等效为LC 回路1,垂直开口处等效为LC 回路2,如图4(a)中蓝色虚框内电路所示.黑色线表示的Ⅱ是双C 结构的透射率变化情况,其透射峰在1.462 THz 处,透射谷分别在1.423 THz 和1.725 THz 处,其中1.423 THz处为基波,高频处1.25 THz 处为二次谐波.结构Ⅰ和Ⅱ作为明模形式存在互相耦合,产生多频带的类EIT 现象[25-28].其中黑色线的仿真对象是在1.0 到1.8 THz 波段的超材料完整结构,仿真结果出现2 个透射峰频点,以及3 个尖锐的透射谷点,2 个透射峰分别在1.438 THz 和1.699 THz 处,3个透射谷分别在1.405 THz,1.543 THz,1.735 THz处.透射峰的峰值分别为0.843 和0.799,透射谷的谷值分别0.019,0.011,0.056.

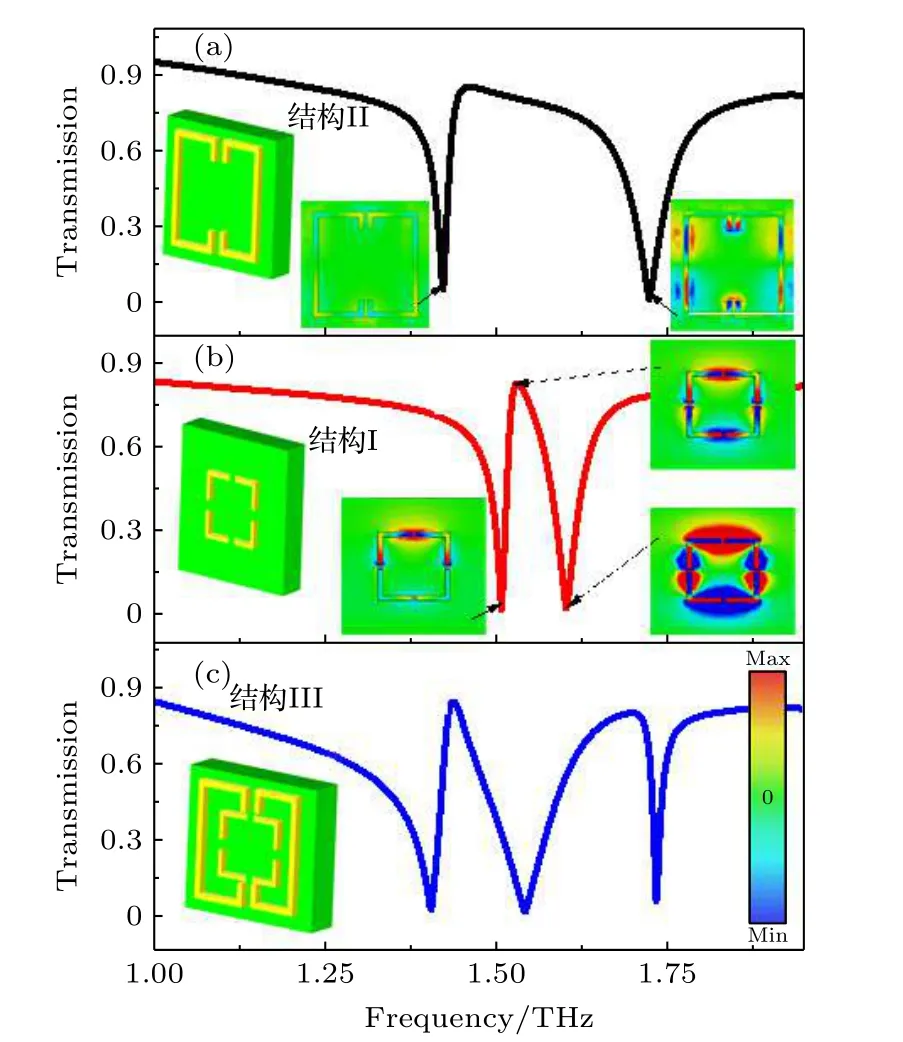
图2 3 种结构 (a)I,(b)II 和 (c)III 的透射频谱图对比及结构 I,II 的对应频点电场分布Fig.2.Comparison of transmission spectra of three structures (a)I,(b)II and (c)III,and corresponding frequency point electric field distribution of structures I and II.

图3 结构Ⅲ条件下各透射峰和透射谷处电磁场分布图 (a)-(e)为电场分布;(f)-(j)为磁场分布图Fig.3.Electromagnetic field distribution on transmission peaks and transmission valleys of the structure III.(a)-(e)are electric field distribution;(f)-(j)is the magnetic field distribution.

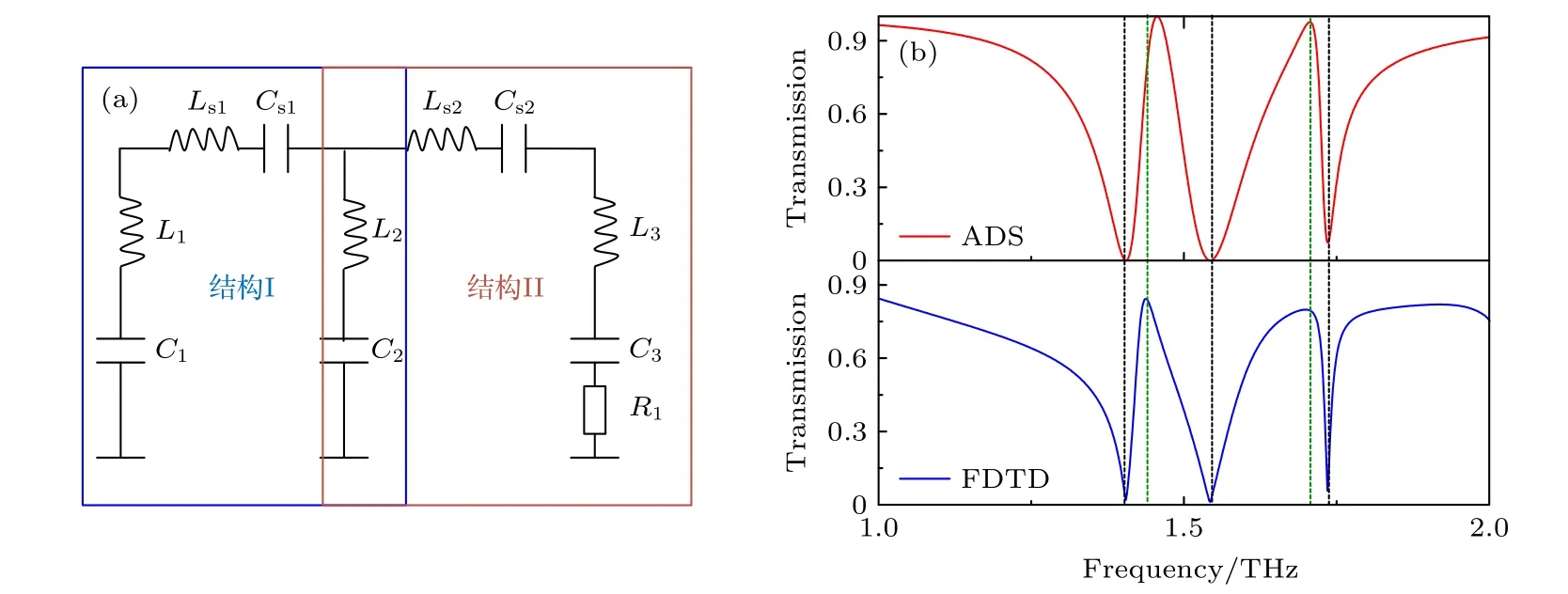
图4 (a)电磁诱导透明的等效电路模型;(b)两种不同方法得到电磁诱导透明效应Fig.4.(a)Equivalent circuit model of electromagnetically induced transparency;(b)electromagnetically induced transparency effect is obtained by two different methods of ADS and FDTD.

为了进一步分析上述结构产生类EIT 的物理机理,图3 分析了图2 结构Ⅲ分别在1.405 THz,1.438 THz,1.543 THz,1.699 THz 与1.733 THz这5 个频点处的电场和磁场分布,如图3 所示.从图3(a)可以看出,在第1 个类EIT 窗口,1.405 THz处,电场主要集中在双C 型结构的开口处,这与图2中透射谱结果一致,即低频处的谐振主要由结构2 的双C 型结构产生1.438 THz 为透明频点,因此电场分布较弱.在1.543 THz 处,能量从外环耦合到内环结构1 的开口处.在第2 个EIT 窗口的情况刚好相反,能量从内环结构I 耦合到外环双C 型结构II 处的开口位置处.图3(f)—3(j)分别为磁场分布的结果,与电场分布的情况刚好相反,在1.438 THz 和1.699 THz 产生了电诱导透明[29].

为了较为清楚地理解EIT 效应的机理,采用等效电路的方法进行分析.如图4(a)所示,该结构Ⅰ可等效为蓝色虚线框内电路,其中L1C1,LS1CS1,L2C2回路分别谐振在结构Ⅰ的低频和高频谐振点,L2C2,LS2CS2,L3C3回路分别谐振在结构Ⅱ的低频和高频谐振点,整个超材料结构可以用完整的电路等效,如图4(b)所示,红色线为根据图4(a)等效电路通过射频电路设计工具ADS 仿真得到,蓝色线为利用FDTD 仿真得到,对比仿真结果可得到利用等效电路解释多波段电磁诱导透明机理.在这个电路模型中,L1C1,LS1CS1,L2C2回路和L2C2,LS2CS2,L3C3回路都作为明模存在,中间的LS1CS1,LS2CS2则表示两个明模之间的耦合[30-33].

4 超材料EIT 结构参数与特性分析

4.1 改变外部双C 的距离

通过改变外部双C 型结构之间的距离,可得到图5 所示结果.从图5 可以看出,改变外部双C 的距离主要会影响低频透射谷,且变化较小,当双C 距离g从0 µm 增大到12 µm 之间时,对第一个透射谷几乎没有影响,在12 µm 之后低频点的透射谷会产生蓝移.当g增大时,1.438 THz 左右的频点的频偏较大,根据图3 的磁场分布能够发现1.438 THz 处磁场主要集中在双C 型结构上.

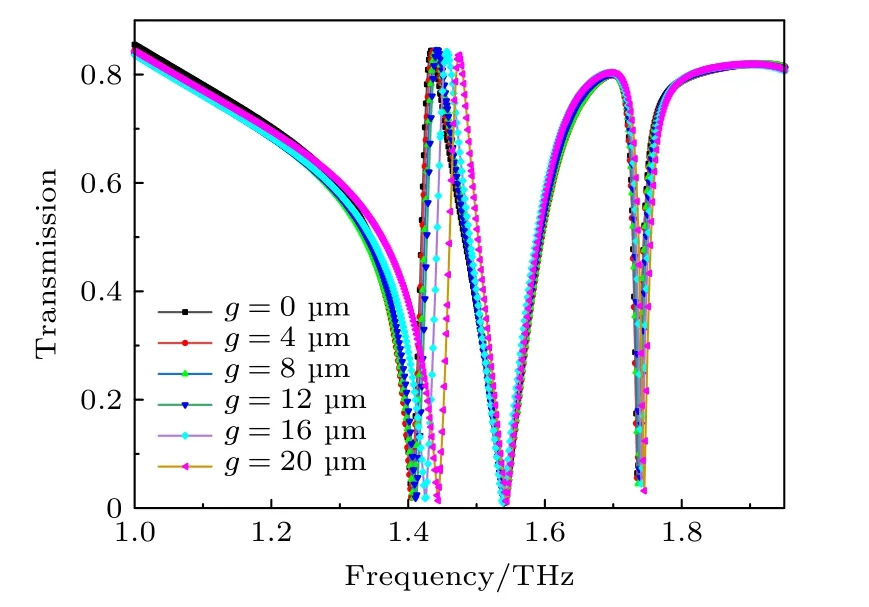
图5 改变空气槽的宽度g 时透射率随频率变化情况Fig.5.Variation of transmission with gap width g of the structure II.

4.2 改变方环水平开口g1 对EIT 效应的影响

为了进一步研究EIT 受超材料结构参数影响情况,如图6 所示通过调节内层方环的水平开口距离大小g1,得到g1对EIT 窗口的影响.在图6 中,红线表示的是在g1=4.0 µm 时的情况.当g1增大时,中间谐振频点会产生蓝移,这是因为中间的谐振频点主要是内环结构Ⅰ产生,从图3 的电场分布来看,在1.543 THz 和1.735 THz 处的电场分布主要集中在内环结构Ⅰ上,因此改变g1会产生较大的影响.当然,由于高频点与中间谐振频点会存在能量耦合,因此中间谐振频点变化会引起高频谐振点的稍微的蓝移,变化范围较小.

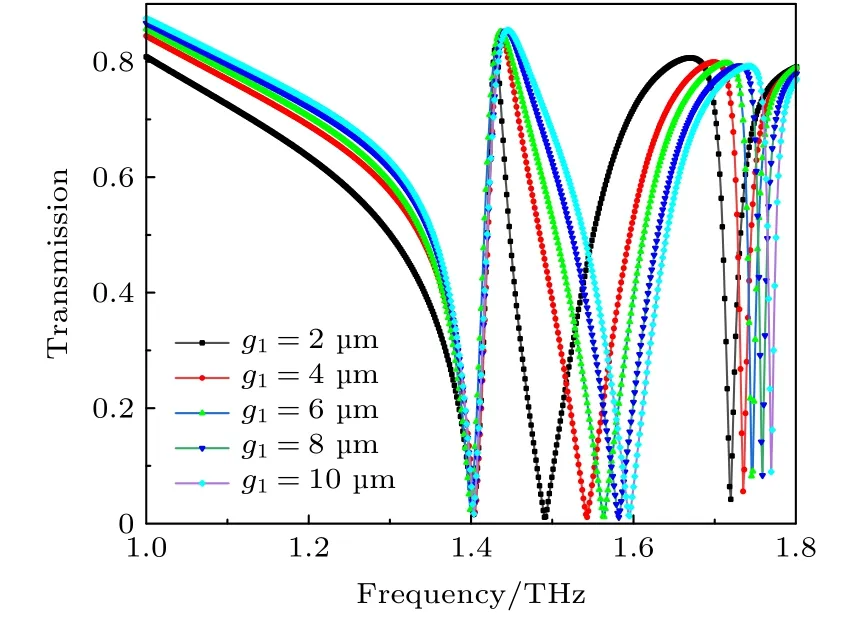
图6 内环结构水平开口大小g1 对EIT 效应的影响Fig.6.Influence of width g1 of the horizontal gap of the structure I on EIT effect.

4.3 改变方环垂直开口大小g2 对EIT 效应的影响

同样的,通过调节内层方环的垂直开口距离大小g2,得到g2对EIT 效应的影响.从图7 可以看出,随着g2的增大,中间谐振频点依旧会发生蓝移,产生的原因和改变方环水平方向开口大小原因相同,但是此时随着g2的增大高频点与中间谐振频点没有产生能量上的耦合,因此中间谐振频点的变化对高频点几乎不产生影响.

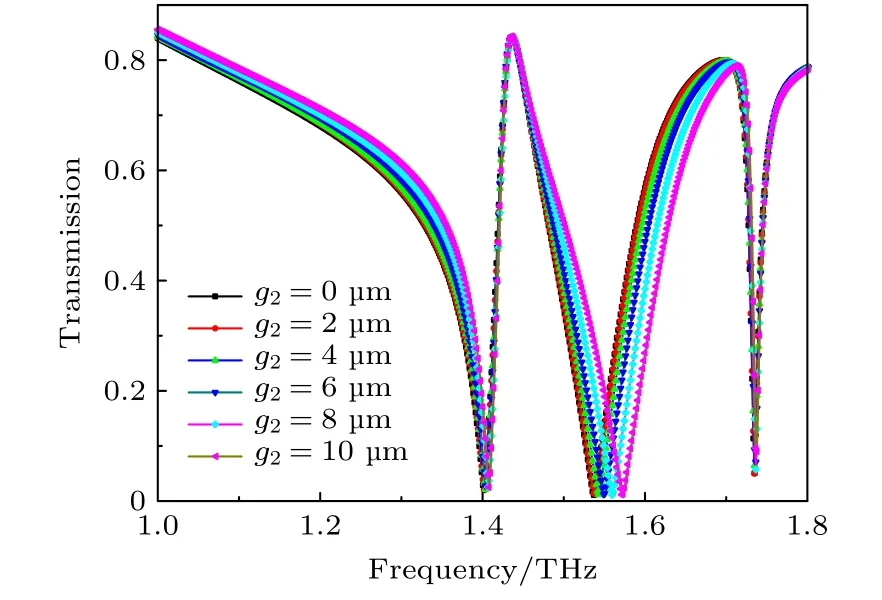
图7 内环结构垂直开口大小g2 对EIT 效应的影响Fig.7.Influence of width g2 of the vertical gap of the structure I on EIT effect.

4.4 改变入射角度

为进一步研究该EIT 效应对入射角度的敏感性,图8 为改变入射角对EIT 效应的影响.从图8可以看到,入射角增大时产生了明显的红移现象,即当入射角改变很小的角度透射谱的变化却很大.因此本结构产生的EIT 效应对入射角度比较敏感.这是由于透射率T在斜入射时与入射角的关系为T=Ticosθ,当入射电磁波角度发生变化时,其透射率也随之变化,因此本结构可作为检测角度变化的传感器使用[34-35].

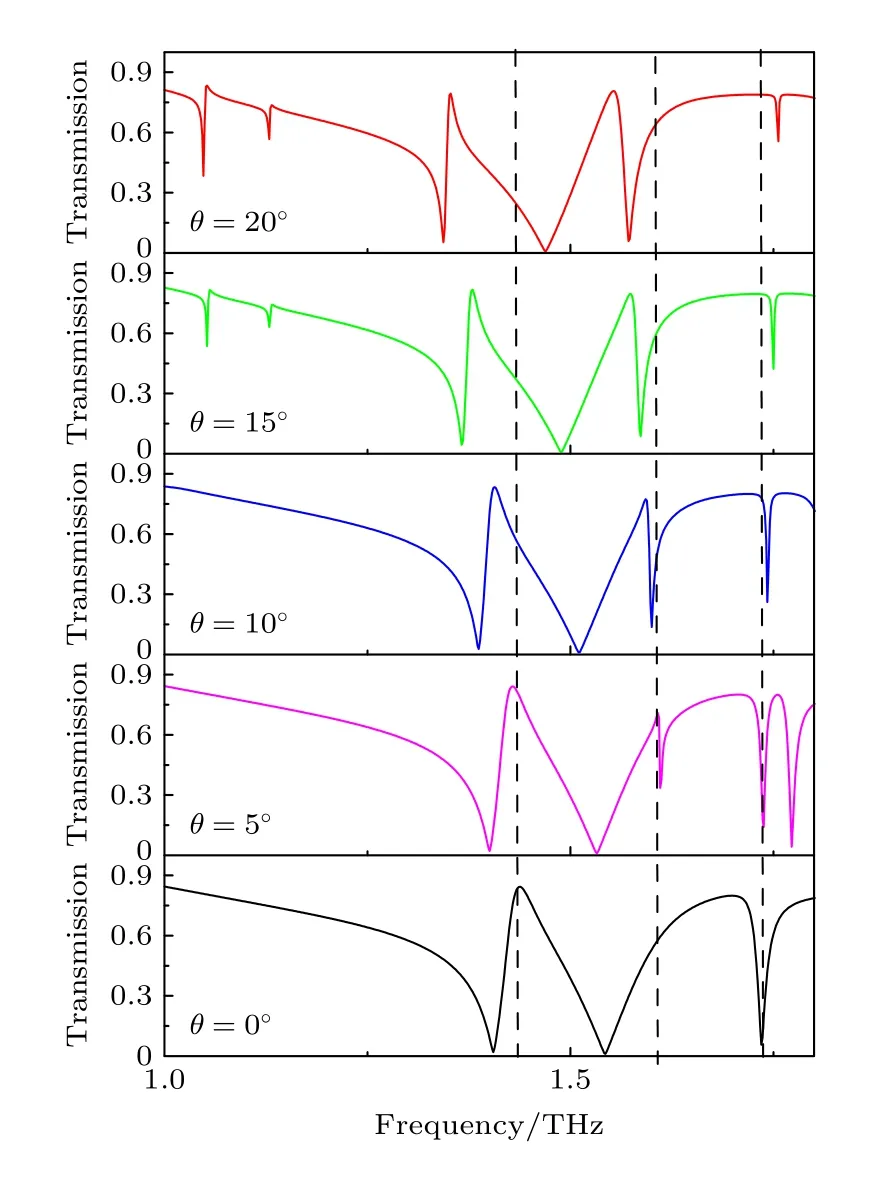
图8 不同入射角度所对应透射谱的变化Fig.8.Variation of transmission spectrum of different incident angles.

4.5 改变背景环境的介电常数

超材料结构通常具有对周围环境介电性质敏感的特性.因此可以作为传感器检测介电特性不同的生物化学样品.在其他参数不变的情况下,改变背景环境的介电常数,不难看出所设计的超材料的谐振频点随着背景环境的介电常数的增加整体发生了红移,由于该结构具有高Q值特性,在折射率传感器方面有潜在的应用(见图9).

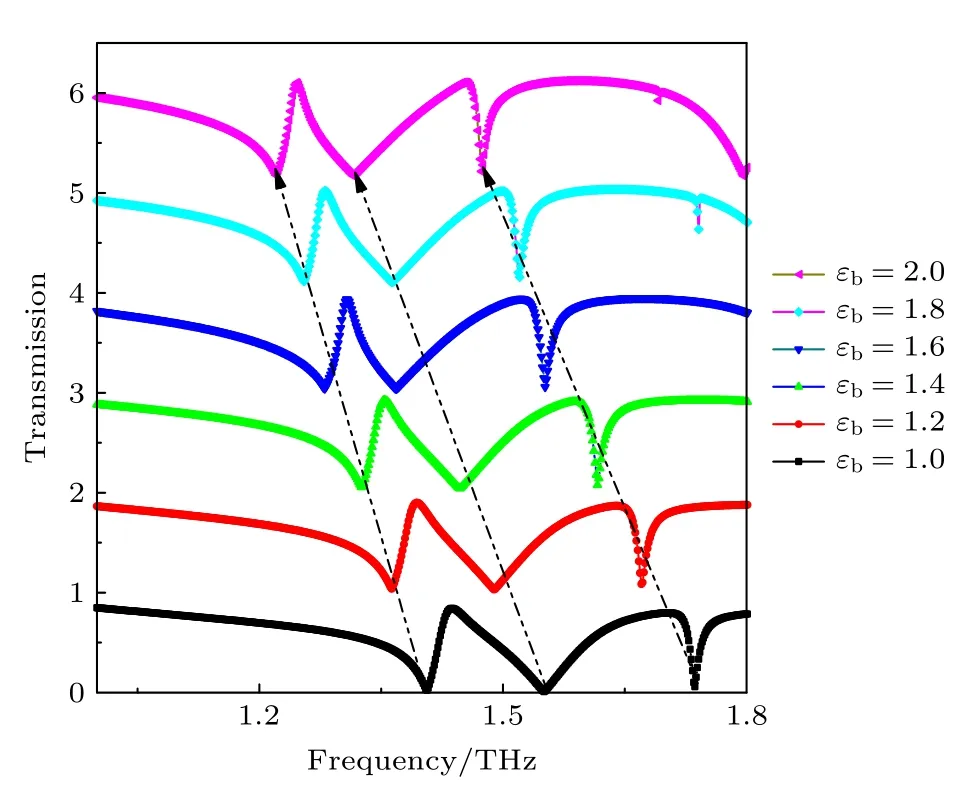
图9 不同背景环境下透射窗的对比Fig.9.Comparison of transmission windows in different background environments permittivity.

5 结论

本文研究了太赫兹波段的角度敏感的类EIT效应.设计了一个双C 型和开口方环为基本单元的超材料结构,所设计的超材料结构模型在1.438 THz和1.699 THz 出现两个透射峰,在1.405 THz,1.543 THz,1.735 THz 出现3 个透射谷,通过比较完整结构和只有双C 型结构,只有开口方环结构分析了透射谱和电场、磁场的能量分布,得到双明模耦合的多频带EIT 效应.利用等效电路分析方法进一步解释了超材料中的类EIT 效应.通过调节方环水平开口大小和方环的垂直的开口大小以及双C 结构距离来讨论结构参数对类EIT 窗口的影响.研究结果表明,所设计超材料结构产生的EIT 效应对角度敏感且当背景环境介电常数发生变化时透射谱线的频点会发生明显的红移,因此本结构在角度传感器、多频滤波器等领域有潜在的应用.