基于有限元计算代理的飞机液压系统管路密封性能评估*

夏芝玮 樊新田 赵旭升 张杰毅 陈 果

(1.西安飞机工业(集团)有限责任公司制造工程部 陕西西安 710089；2.南京航空航天大学民航学院江苏南京 211106；3.南京航空航天大学通用航空与飞行学院 江苏溧阳 213300)

现代飞机液压系统逐渐向更高压力发展，而管路结构的强度储备很低，相关安装控制标准已经不能满足目前飞机管路系统的安装控制要求，大量管路系统出现了密封问题，泄漏故障居高不下，成为了飞机管路系统的主要故障，严重影响了我国新型飞机的设计研发速度以及排故速率。

目前，国内外学者对管路泄漏进行了广泛研究。文献[1]研究了航空镀镉45钢和钛合金导管连接件在模拟服役环境中的气密性、油压气密性以及应力腐蚀、表面腐蚀等性能。文献[2-4]利用有限元法对管路锥形密封结构和双锥形管接头密封连接结构的密封性进行了研究，分析了设计参数对密封性的影响。文献[5]研究了航空发动机钛合金管路连接副在拉伸载荷下的密封性能,建立了管路连接副在拉伸载荷下的多体弹性接触模型，研究了连接副密封面的接触力、接触面积和接触应力随拉力的变化规律。文献[6]采用正交试验研究了管接头拧紧力矩的主要影响因数。文献[7-8]分析了管接头在弹塑性小变形条件下，载荷及应力沿密封面的分布规律。文献[9]采用试验和仿真相结合的方法分析管接头在动力学载荷条件下的应力松弛情况。文献[10]计算了管接头在拧紧力矩作用下密封带宽度，并进行了试验验证;此外，还建立管接头拧紧力矩与密封带之间关系，为工程中管接头拧紧力矩的确定提供理论依据。

但是，目前关于管路连接件密封性的研究中均未考虑装配偏差所带来的管道系统连接件装配应力对连接件密封性能的影响。而在工程实际中，由于装配偏差所带来的管路连接件装配应力是飞机导管渗漏的关键因素。本文作者基于有限元分析方法，建立管道连接件模型，通过静力学仿真计算研究在轴向装配偏差下密封面参数的变化规律及影响参数，并基于支持向量机回归模型对有限元仿真结果进行数据拟合，得到管接头拧紧力矩、管接头接触面摩擦因数以及轴向装配偏差与密封性能指标之间的函数关系，从而建立起有限元的计算代理模型，以期用该回归模型代替大量耗时的有限元计算过程。研究结果为实际飞机管道安装中装配参数的控制提供理论依据。

1 基于有限元计算代理的飞机液压系统管路密封性能评估方法

1.1 总体流程

图1所示为基于有限元计算代理的飞机液压系统管路密封性能评估方法流程，主要包括3个部分，即管道密封性能的有限元仿真、仿真数据拟合以及管道密封性能预测与评估。

图1 基于有限元计算代理的飞机液压系统管路密封性能评估方法流程Fig 1 Flow of pipeline sealing performance evaluation method for aircraft hydraulic system based on finite element calculation agent

其中，管道密封性能的有限元仿真分析是首先建立复杂的有限元模型，然后利用拉丁超立方采样方法得到拧紧力矩、摩擦因数和轴向偏差在参数域的样本点，最后通过有限元仿真分析得到管道密封参数，获取大量仿真数据样本。仿真数据拟合是利用支持向量机回归分析方法对仿真数据进行拟合，基于输入-输出等效的原则，得到管路密封性能的有限元计算代理模型。管道密封性能预测与评估是指在实际管道设计和装配中，输入不同的拧紧力矩、摩擦因数和轴向偏差，代入代理模型，预测出当前参数下的密封性能，并对管路密封状态进行评估。

1.2 关键技术

1.2.1 管道密封性能的有限元仿真

图2所示为管道密封性能的有限元仿真分析过程。首先根据管路连接件的尺寸标准，利用Catia软件建立几何模型；然后利用Hypermesh软件进行有限元网格划分，并定义接触和约束、施加螺栓预紧力和管道轴向偏差等；最后将所建立的有限元模型导入到ANSYS软件，在不同的拧紧力矩、摩擦因数和装配偏差下进行仿真分析，得到管道密封面宽度。

图2 管道密封性能的有限元仿真流程Fig 2 Finite element simulation flow of pipeline sealing performance

1.2.2 仿真数据拟合

在得到大量仿真样本后，需要对数据进行非线性拟合，从而得到反映拧紧力矩、摩擦因数及轴向安装偏差对管道密封性能的影响关系表达式，并以此作为有限元模型的计算代理，用于对其他参数下的管道密封性能进行预测和评估。其方法流程如图3所示。

图3 管道密封性能仿真数据回归分析Fig 3 Regression analysis of pipeline sealing performance simulation data

由于该问题为典型的多元非线性回归分析问题，文中引入具有小样本优越学习能力的支持向量回归(Support Vector Regression,SVR)方法对样本数据进行回归分析和建模，从而得到管路连接件拧紧力矩、摩擦因数及装配偏差与密封性能之间的函数关系表达式。

对于给定的训练样本{(xi,yi),i=1,2,…,n}，xi为输入向量，yi为与之对应的期望输出向量。SVM用一个非线性映射φ将输入向量映射到一个高维特征空间，并进行线性回归，其回归函数为

f(x)=w·φ(x)+b

(1)

式中：w、b分别为权向量和阈值；w·φ(x)为w与φ(x)的内积，并且满足结构风险最小化原理。

对优化目标函数求极值

(2)

K(xi,xj)=exp{γ|xi-xj|2}

(3)

式中:γ为核函数参数。

用核函数K(xi·xj)来替代内积运算，可以实现由低维空间到高维空间的映射，从而使低维空间的非线性问题转化为高维空间的线性问题。

引入核函数后，优化目标函数变为如下形式：

(4)

相应的预测函数变为

(5)

利用式(5)就可直接建立支持向量机的回归模型。

基于结构风险最小化的支持向量回归预测方法，在理论上保证了小样本学习下的模型泛化能力。因此，在取值范围合理的情况下，SVM模型采用不多的训练样本，就能够准确逼近非线性函数。

1.2.3 管道密封性能的预测与评估

图4所示为管道密封性能的预测和评估流程。在设计和装配过程中，需要研究在一定的拧紧力矩和密封面的摩擦因数配合下，能够容许的轴向装配偏差。因此，可以利用所得到的有限元代理模型，进行准确快速地预测和评估，避免了大量的有限元计算工作，从而大大地提升了管道设计和装配工作效率；同时，也可为指定合适的制造和装配标准和规范提供指导。

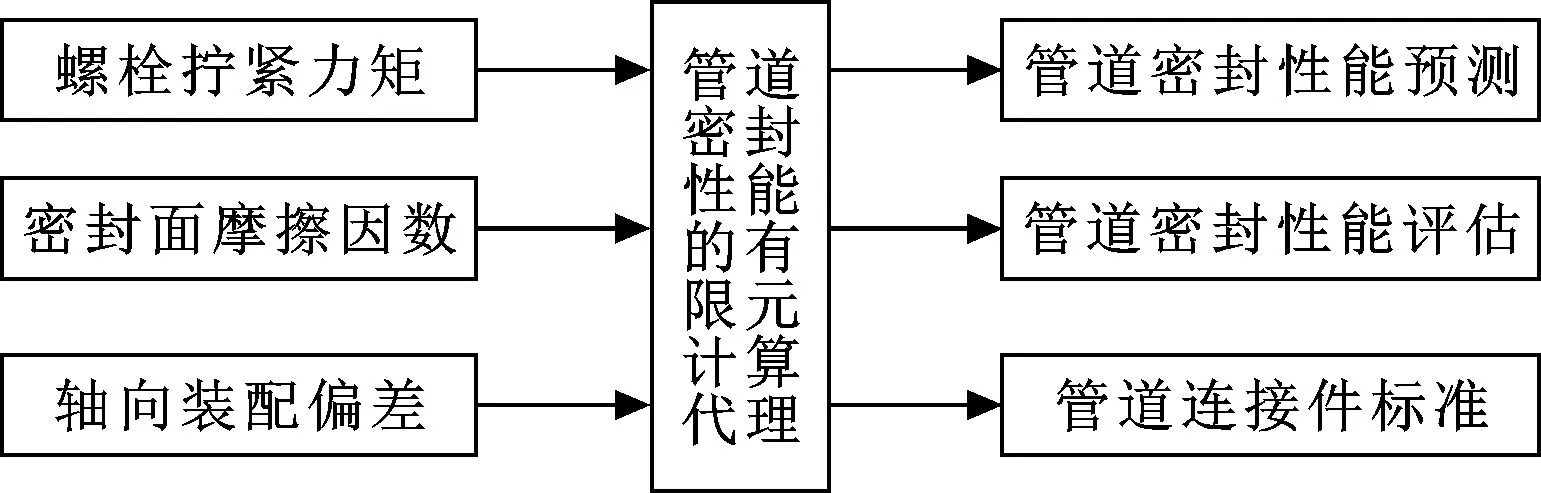
图4 管道密封性能的预测与评估Fig 4 Prediction and evaluation of pipeline sealing performance

2 基于有限元计算代理的飞机液压系统管路密封性能评估算例

2.1 飞机管路连接件有限元模型

2.1.1 管路连接件结构

文中研究的管路连接件采用扩口式管接头，并选取常用的37°扩口角。如图5所示，管接头连接件主要由管接头、扩口管、平管嘴和外套螺母4部分组成。管接头和外套螺母的连接采用螺纹紧固的方式。在管接头和扩口管的连接过程中，管端在加工过程中形成的扩口锥面与管接头锥面相互配合，面与面紧贴在一起，从而形成金属接触的面面密封。平管嘴处于扩口管和外套螺母之间，在压紧扩口管与管接头的同时可以避免管路在复杂工作环境中，在扩口交界处产生的应力集中，将扩口管路的剪切应力分散，可以有效提高管接头连接强度。管接头与外套螺母在拧紧力矩作用下压紧扩口管与管接头并出现塑性形变，形成密封面[11]。参考HB699—2002，文中采用的第一尺寸系列内径为10mm的直通管接头标准如表1和表2所示。如图5所示文中选取外径为10 mm的管道连接件为研究对象。

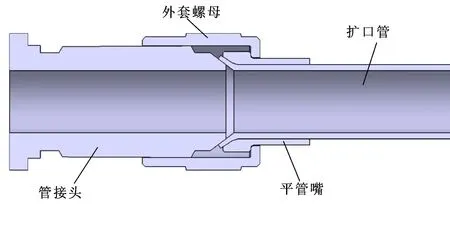
图5 管接头连接件CATIA模型Fig 5 CATIA model of pipe connector

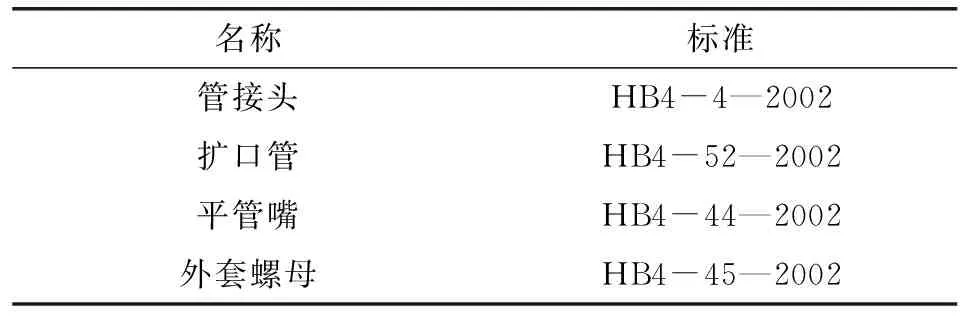
表1 管路连接件尺寸标准Table 1 Dimension standard of pipeline connector

表2 管路及连接件为钢件时拧紧力矩要求Table 2 Tightening torque requirements for steel pipe and connector

2.1.2 材料本构模型

扩口管道使用1Cr18Ni9Ti材料[12]，平管嘴使用1Cr11Ni2W2Mov材料[13]，外套螺母与直通管接头使用TC6材料[14]。表3给出了材料的属性与力学性能。

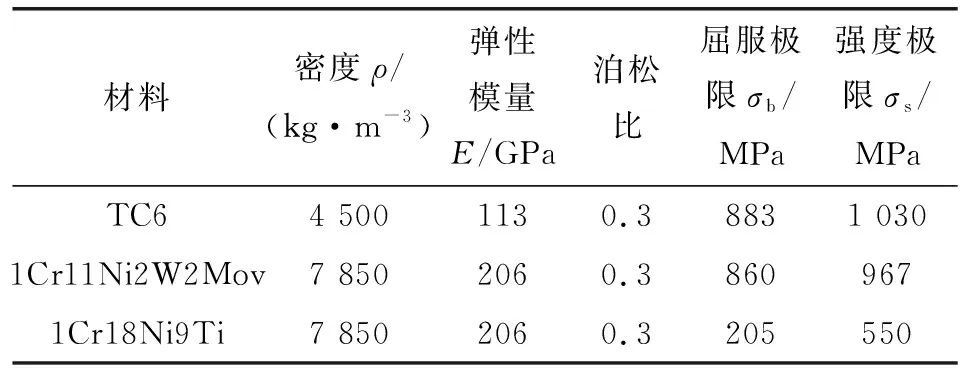
表3 材料力学特性Table 3 Mechanical Properties of materials

2.1.3 有限元模型

在将CATIA中构建好的三维模型导入Hypermesh进行有限元网格划分。图6所示为管路连接件的有限元模型。管接头、扩口管、平管嘴和扩口管网格数分别为47 088、42 408、7 884和14 724，共计112 104个。

对于扩口管路连接件，在ANSYS计算前需要明确和各部件间的接触问题。接触问题也是一种非线性计算问题，需要大量的计算资源，因此求解前一定要选取合适的接触方式和接触算法等。ANSYS中对于接触的设置主要分为刚-柔接触和柔-柔接触，同时又根据接触形式分为点-点接触、点-面接触、线-面接触和面-面接触。根据文中探讨的扩口处密封性问题，考虑采用柔-柔接触和面-面接触。根据不同接触类型的特点，为了模拟管接头和外套螺母处螺纹约束的状态，采用no separation接触；而其余3个接触要考虑摩擦产生的相对滑动等影响，因此采用standard接触。

扩口管路系统属于典型的螺纹连接，在ANSYS仿真软件中，要求将拧紧力矩转化为预紧力以方便后续的加载。对于扩口管路系统，拧紧力矩T主要用于克服外套螺母同平管嘴间摩擦接触的摩擦力矩T1以及外套螺母同直通管接头螺纹连接处的摩擦力矩T2。

平管嘴和外套螺母摩擦力矩T1为

T1=Fμr2

(6)

螺纹连接处摩擦力矩T2为

(7)

总拧紧力矩T为平管嘴和外套螺母处摩擦力矩T1和螺纹连接处摩擦力矩T2之和，即

(8)

(9)

式中：F为轴向预紧力；r1为螺纹中径的1/2；μ为摩擦因数；R和r分别为平管嘴和外套螺母接触环的内外圈半径；P为螺距；θ为螺纹半角，螺纹半角为30°。

根据航空工业标准HB4-4-2002，P=1.5 mm，θ=30°，r1=8.51 mm，R=8 mm，r=7.1 mm。经计算r2=7.55 mm。将已知量代入式(8)，可得拧紧力矩、轴向预紧力和摩擦因数之间的关系为

T=F(0.238 7+17.377μ)

(10)

拧紧力矩转化为轴向载荷，施加到外套螺母右端面节点上，以此模拟管路的预紧状态;管接头的右端面节点施加固定约束。除了上述边界条件，文中还需要分析偏差对管路应力状态和密封特性的影响。文中将轴向偏差以强制位移的形式添加在扩口管的左端面节点上，如图6所示。

图6 约束及载荷的施加Fig 6 Application of constraint and load

2.1.4 密封性评价指标及提取方法

管接头锥面和扩口管喇叭口面在预紧力作用下形成金属面-面密封，即扩口管面(低硬度面)发生塑性形变，填满管接头锥面(高硬度面)表面微观缝隙。其密封性能可通过接触面上最小密封宽度、平均密封宽度、密封面积以及平均密封压力进行评价。

密封宽度的定义是指接触面上接触压力超过扩口管(低硬度面)屈服极限部分的宽度。密封宽度越大则密封性能越好，反之亦然。密封宽度能够最为直观地表现出密封与否，在管道受到外载时，密封宽度可能不均匀，其中最小密封宽度为最窄的宽度，平均密封宽度为所有圆周角度上的密封面宽度的平均值，密封面积为所有接触压力超过扩口管屈服极限部分接触面积，平均密封压力为密封面积上的平均接触压力。文中拟用这4个指标来评价密封性能。

由表3可知，扩口管路材料1Cr18Ni9Ti的屈服强度为205 MPa，而管接头材料TC6的屈服强度达到883 MPa。因此，当接触压力大于205 MPa时，扩口管与管接头金属面面接触间产生一定的塑性变形，从而填充两金属面间细小的缝隙，达到一定的密封效果。因此，文中认为接触应力达到205 MPa的位置处于密封状态，并根据处于密封状态的最小宽度确定密封面宽，进而判断扩口管和管接头面面接触整体的密封状态。

2.2 基于飞机管路连接件有限元模型的密封性能仿真计算

2.2.1 多参数空间的拉丁超立方采样

利用所建立的飞机管路连接件有限元模型仿真分析拧紧力矩、密封面摩擦因数以及轴向装配偏差对管路密封性能的影响时，由于有限元仿真计算效率较低、计算负荷很大，因此需要设计仿真实验，利用能够尽可能地均匀填充所有样本空间的少量样本进行有限元仿真计算。试验设计是解决怎样合理安排离散点数据进行抽样试验的数学方法，它是构造代理模型时所采用的取样策略，决定了所需样本点的个数和这些点的空间分布情况。研究表明，试验设计直接影响着代理模型的逼近精度和构建效率。对于试验设计的一个基本要求是样本点在参数空间中分布均匀，在参数空间中各个部分的样本点密度基本一致，样本点之间的相对距离也基本相同，并且样本点的分布应该满足各向同性，即样本点应“既不重复，也不遗漏”地充满整个参数空间。拉丁超立方抽样(Latin hypercube sampling)是一种常用的参数空间抽样算法。

图7所示为摩擦因数、拧紧力矩以及轴向偏差3个参数的拉丁超立方抽样结果，其中摩擦因数的范围为0.05～0.3，拧紧力矩的范围为30～50 N·m，轴向偏差为-0.3～0.3 mm，采样点数为100。可以看出，采用拉丁超立方方法抽取出来的样本点均匀地分布在整个参数空间。

图7 3个参数空间的拉丁超立方抽样结果Fig 7 Latin hypercube sampling results for three parameter spaces

2.2.2 基于SVR的回归分析结果

通过仿真计算得到摩擦因数、拧紧力矩及轴向偏差与4个密封性能指标(最小密封宽度、平均密封宽度、密封面积、平均接触压力)的数据集。对4个仿真数据集进行支持向量回归分析建模得到反映4个密封指标的SVR模型，训练中采用10折交叉验证和网格搜索法得到最优的模型参数，利用所有仿真数据测试模型的拟合能力，比较预测值和实际值的差异，并以此评定拟合模型的准确性和有效性。图8所示为各个密封指标的预测值和实际值的比较，表4给出了预测值和实际值的均方误差以及平方相关系数。从表4和图8可以看出，SVR回归分析达到了较高的拟合精度和推广能力。

图8 SVR回归模型的预测值与实际值的比较Fig 8 Comparison of predicted values and actual values of SVR regression model (a) SVR model of minimum sealing surface width; (b) SVR model of average sealing surface width;(c) SVR model of sealing area；(d) SVR model of average contact pressure

表4 最优回归模型参数及评定指标Table 4 Parameters and evaluation indexes of optimal regression model

2.3 摩擦因数对密封性能的影响

为了验证SVR预测模型的正确有效性,分别利用得到的4个SVR回归模型预测了摩擦因数对密封性能的影响，并与有限元仿真结果进行对比。计算条件为：拧紧力矩40 N·m，轴向装配偏差为0，摩擦因数为0.05～0.3。图9所示为最小密封面宽度SVR模型、平均密封面宽度SVR模型、密封面积SVR模型及平均接触压力SVR模型的预测结果与有限元仿真结果的比较。可以看出，4个有限元代理模型与有限元仿真结果达到了很好的一致性。图9结果表明在拧紧力矩一定的情况下，密封面上的摩擦因数越大，密封面宽度和面积均有一定程度增加，但是密封面平均接触压力将出现下降，使得密封性能变差。

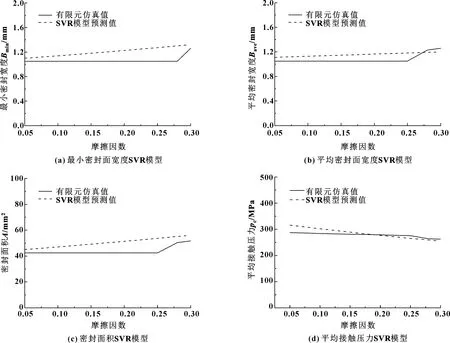
图9 SVR模型预测与有限元仿真的摩擦因数对密封性能的影响规律比较Fig 9 Comparison of the influence of friction coefficient on sealing performance with SVR models prediction and finite element simulation (a) SVR model of minimum sealing surface width;(b) SVR model of average sealing surface width; (c) SVR model of sealing area;(d) SVR model of average contact pressure

2.4 拧紧力矩对密封性能的影响

为了验证SVR预测模型的正确有效性,分别利用得到的4个SVR回归模型预测了拧紧力矩对密封性能的影响规律，并与有限元仿真结果进行对比。计算条件为：摩擦因数为0.1，轴向装配偏差为0，拧紧力矩为30～50 N·m。图10所示为最小密封面宽度偏差SVR模型、平均密封宽度SVR模型、密封面积SVR模型以及平均接触压力SVR模型的预测结果与有限元仿真结果的比较。可以看出，4个有限元代理模型与有限元仿真结果达到了很好的一致性。图10结果表明在摩擦因数一定的情况下，拧紧力矩越大，密封宽度、密封面积和密封压力均增加，因此密封性能越好。

图10 SVR模型预测和有限元仿真的拧紧力矩对密封性能的影响规律比较Fig 10 Comparison of the influence of tightening torque on sealing performance with SVR models prediction and finite element simulation (a) SVR model of minimum sealing surface width；(b) SVR model of average sealing surface width； (c) SVR model of sealing area;(d) SVR model of average contact pressure

2.5 装配偏差对密封性能的影响

为了验证SVR预测模型的正确有效性,分别利用得到的4个SVR回归模型预测了装配偏差对密封性能的影响规律，并与有限元仿真结果进行对比。计算条件为：摩擦因数为0.1，拧紧力矩为40 N·m，轴向偏差为-0.3～0.3 mm。图11所示为最小密封面宽度SVR模型、平均密封面宽度SVR模型、密封面积SVR模型以及平均接触压力SVR模型的预测结果与有限元仿真结果的比较。可以看出，4个有限元代理模型与有限元仿真结果达到了很好的一致性。图11结果表明在摩擦因数和拧紧力矩一定的情况下，轴向偏差对密封性能有一定影响，轴向偏差从负到正增加，密封性能变得更好，密封面宽度和面积逐渐增加，但是密封面平均接触压力则表现为先减后增。

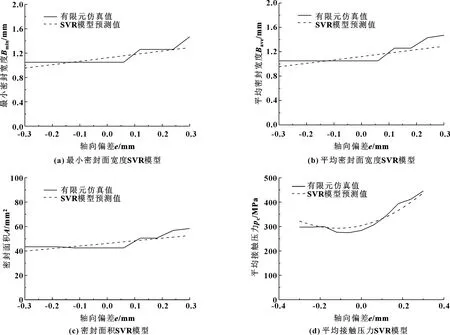
图11 SVR模型预测和有限元仿真的轴向装配偏差对密封性能的影响规律比较Fig 11 Comparison of the influence of axial assembly deviation on sealing performance with SVR models prediction and finite element simulation(a) SVR model of minimum sealing surface width；(b) SVR model of average sealing surface width；(c) SVR model of sealing area；(d) SVR model of average contact pressure

3 结论

(1)建立飞机液压系统管路连接件有限元模型，选择摩擦因数、拧紧力矩及轴向装配偏差3个对管道密封性能有重要影响的因素，以及最小密封面宽度、平均密封面宽度、密封面积以及平均接触压力4个密封指标，研究3个因素对密封性能的影响。

(2)对3个因素的取值空间进行拉丁超立方采样，通过有限元仿真计算得到大量的仿真样本；然后，利用支持向量机回归模型对仿真数据进行拟合，得到有限元计算代理模型。

(3)利用有限元代理模型代替复杂的有限元计算对管路密封性能进行评估，比较了有限元仿真结果和代理模型计算结果，验证了有限元代理模型的正确有效性。

(4)分析了拧紧力矩、摩擦因数、轴向装配偏差等3个因素对管路密封性能的影响规律,结果表明：在拧紧力矩一定的情况下，密封面上的摩擦因数越大，密封面宽度和面积均有一定程度增加，但是密封面平均接触压力将出现下降，因此密封性降低；在摩擦因数一定的情况下，拧紧力矩越大，密封宽度、密封面积和接触压力均增加，因此密封性增加；在摩擦因数和拧紧力矩一定的情况下，轴向偏差对密封性能有一定影响，轴向偏差从负到正增加，密封性能变得更好，密封面宽度和面积逐渐增加，但是密封面接触压力则表现为先减后增。