基于自抗扰技术的直驱永磁同步电机无传感器控制*

刘宇佳, 孟克其劳,2,3, 海日罕, 王 腾, 马剑龙,2,3

(1.内蒙古工业大学 能源与动力工程学院,内蒙古 呼和浩特 010051；2.风能太阳能利用技术教育部重点实验室,内蒙古 呼和浩特 010051；3.内蒙古自治区风电技术与检测工程技术研究中心,内蒙古 呼和浩特 010051)

0 引 言

直驱永磁同步电机(direct drive permanent magnet synchronous motor,DPMSM)具有结构简单、运行可靠且效率较高等优势,被广泛应用于工业、交通、军事等领域[1,2]。因DPMSM是一个多变量、强耦合的非线性系统,传统的PI控制器无法满足其高性能控制的要求,因此,滑模控制、模糊控制、自适应控制等方法被引入永磁同步电机(PMSM)的控制[3]。自抗扰控制器(active disturbance rejection controller,ADRC)的核心思想是以简单的积分串联型为标准型,把系统动态中不同于标准型的部分视为总扰动,实时地对总扰动进行估计并加以消除[4]。ADRC由跟踪微分器(tracking differentiator,TD)、扩张状态观测器(extended state observer,ESO)和非线性状态误差反馈(nonlinear state error feedback,NLSEF)控制律三部分组成[5]。文献[6]在速度外环和电流内环中均采用ADRC,虽可减小超调量,但参数较多,且调节过程较为复杂。文献[7]在ESO中加入积分滑模结构,提高了PMSM控制性能。文献[8]提出了一种PMSM线性ADRC的设计方法,使电机无超调启动,但突加负载时仍有少部分超调量。

无位置传感器控制因降低系统成本和提高系统可靠性等优势,被广泛应用于电机控制。常用的无位置传感器控制方式主要有模型参考自适应法(model reference adaptive system,MRAS)、扩展卡尔曼滤波(extended Kalman filtering,EKF)法和滑模观测器(sliding mode observer,SMO)法等[9]。文献[10]对PMSM采用MRAS对转速进行辨识,但控制调节过程较为复杂。文献[11]采用离散化方程的EKF法,对PMSM转子位置和转速进行辨识,虽动态估算性能较好,但需要对协方差矩阵进行位置求逆运算且计算量较大。文献[12]提出双级式的模糊自适应系统,相较于传统的PMSM矢量控制系统鲁棒性显著提高。文献[13]在SMO中用改进的饱和函数取代传统开关函数,虽对外界环境干扰和参数变化不敏感,但负载变化时系统响应不迅速。

针对上述问题,本文在ADRC中设计了一个新型的非线性控制函数,此函数相较于传统函数,在原点具有较好平滑性,同时采用改进后的SMO对电机转速和转子位置角进行观测。仿真结果表明,改进后的控制系统可有效抑制负载突变时对转速的影响,且具有较强鲁棒性。

1 PMSM的数学模型

PMSM是非线性系统,为简化PMSM的数学模型,应假设转子中不含阻尼绕组、定子绕组为三相对称分布、并且忽略涡流、磁饱和和磁滞损耗[14]。本文选用表贴式PMSM进行分析。其电压方程如下

(1)

式中uα,uβ为α-β坐标系下的电压分量；iα,iβ为α-β坐标系下的电流分量；R为定子电阻；L为定子电感;ψf为永磁体磁链；ω为电角速度。电磁转矩方程为

(2)

式中Te为电磁转矩；Pn为极对数；ψα,ψβ为α-β坐标系下的磁链分量。

机械运动方程为

(3)

式中J为转动惯量；TL为负载转矩。

2 ADRC的改进

2.1 传统型ADRC

ADRC中跟踪微分器为设定的输入信号安排过渡过程,得到微分信号,并对输入信号产生滤波效果。ESO不仅可以估计系统中的状态变量,而且可以得到系统内外扰动的估计值。NLSEF控制律输出系统控制信号,改进控制效果。其基本结构如图1所示。

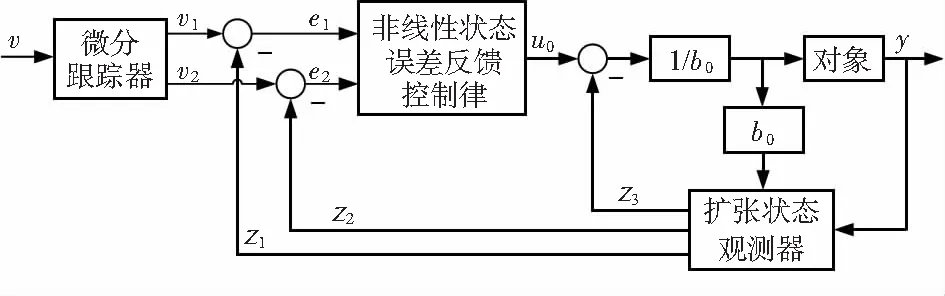
图1 ADRC基本结构

其中一阶ADRC为

跟踪微分器(TD)

(4)

扩张状态观测器(ESO)

(5)

NLSEF控制律

(6)

其中,传统非线性函数为

(7)

式中fal(e,α,δ)为非线性控制函数；e为误差信号；α为非线性因素；δ为滤波因子。

2.2 改进型ADRC

因为非线性函数是ADRC算法的核心部分,而传统的fal函数在分段点和原点处不可导,此函数连续性和平滑性较差,因此本文对传统fal函数进行改进优化,改进的新非线性函数为nfal。

当|e|>δ时,采用双曲正切函数tanh代替符号函数sign。tanh的表达式为

(8)

sign函数与tanh函数曲线对比如图2。

图2 sign函数与tanh函数曲线

由图2可知,tanh函数在实数域内是连续的,而且在零点处函数值为零,通过调节系数a的值进而调节tanh(ax)的陡度,因此要合适选取a的值,进一步提高控制效果。

当|e|≤δ时,令新函数nfal为

nfal(e,α,δ)=ζ1sine+ζ2e2+ζ3tane

(9)

对式(9)进行插值拟合,其过程满足可导连续的条件,当e=δ和e=-δ时,式(10)成立

(10)

解得

(11)

综上所述,改进后的新非线性函数nfal为

(12)

通过分析上述表达式可知,由于e2项系数为0,因此,插值拟合后所得的新非线性函数的收敛性更好。

在改进后的新非线性函数nfal相较于传统的fal函数连续性和平滑性更佳。将式(7)中的fal函数用式(12)替代,可以得到新的ADRC。

3 SMO的改进

3.1 传统型SMO

在PMSM无位置传感器控制中,SMO用来观测电机的状态变量,先选定一个滑模面,通过控制使状态变量沿着滑模面移动,并在电流条件下构建状态方程。

定义滑模面

s(x)=s-is

(13)

将由磁转矩方程变换为电流方程,并构建SMO,随后将二者将相减得到

(14)

根据滑模控制原理,当运动点的轨迹运动到滑模平面时,同时考虑到反电动势时,有

(15)

由式(15)可知符号函数的输出通过增益放大后等效于反电动势,低通滤波器(LFP)将会滤除系统中的高频谐波和干扰信号

(16)

式中ωc为低通滤波器截止频率。

经过数学运算得到转速

(17)

(18)

低通滤波器滤波过程中会引起相位延迟,因此需引入一个参数,对其进行补偿

(19)

(20)

3.2 改进型SMO

传统的SMO控制函数采用符号函数使状态变量在滑模面两侧运动,存在较为严重的抖振现象,为了解决此问题,本文采用双曲正切函数(tanh)取代符号函数(sgn),很大程度削减了抖振。改进后的SMO为

(21)

综上所述,改进后的SMO程序框图如图3所示。

图3 滑模观测器基本结构

当滑模增益K较大时,抖振也会随之增大,但系统的鲁棒性较好,当K较小时观测器将会失灵,因此需适当选取K值。

3.3 改进型SMO稳定性分析

首先选取正定的李亚普诺夫函数

(22)

选取滑模面

(23)

要保证系统渐近稳定,则

(24)

(25)

4 仿真与分析

为了验证改进后ADRC和SMO的可行性和有效性,在MATLAB/SIMULINK中搭建了仿真模型,该模型由PMSM、PWM变换器和控制策略等组成。采用改进后的ADRC取代传统PI控制器,通过基于双曲正切函数的SMO获取速度位置信息,本文采用id=0的矢量控制策略,系统原理框图如图4所示。

图4 系统控制原理框图

图5 电机转速对比

由图5得,传统的PI控制器和传统的SMO所得转速曲线图虽在启动时和突加负载时响应较快,但超调量较大,且维持在参考转速内时间较长。将传统PI控制器替换为传统的ADRC后,转速虽可以快速且无超调的恢复在参考转速,但相较于改进后的控制系统而言,突加负载时转速跌落大且恢复时间较长。因此改进后的控制系统,应对负载突变时响应较快,且恢复到参考转速所需时间较短,此系统控制性能较好。如图6所示。

图6 电机估计转速与实际转速曲线

由图6得,改进后的控制系统估计转速对实际转速可以很好地进行实时跟踪,两者几乎重合,误差较小,基本达到稳态效果。如图7所示。

图7 电机转速估计值与实际值误差

由图7得,改进后的控制系统对电机转速的估计精度大幅度提高,电机转速的估计值与实际值误差大幅度减小。如图8所示。

图8 三相定子电流波形

由图8得,0.2 s前电机空载运行,电机三相电流在零附近波动,0.2 s后电机突加负载,电流可迅速变化平滑,且正弦性较好。转子位置估计值与实际值及其误差,如图9,图10所示。

图9 转子位置估计值与实际值

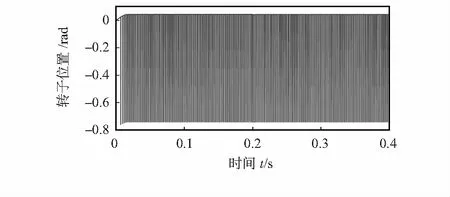
图10 转子位置估计值与实际值误差

由图10得,在系统稳定运行后,SMO得到的转子位置估计值和电机运行过程中的实际位置误差很小,且稳定在-0.72左右,因此证明通过SMO输出的转子位置精度较高。电机输出转矩如图11所示。由图11得,改进后的系统在0.2s时加入负载扰动,转矩波动较小,同时可以快速稳定到相应转矩。

图11 电机输出转矩

5 结 论

本文采用改进ADRC和SMO对PMSM控制系统进行优化,其中改进型ADRC采用了一个在原点具有更好平滑性的新型非线性函数,在SMO中为削弱抖振现象,采用了一种基于双曲正切函数的改进型SMO。通过仿真结果表明：改进后的控制系统能够提高系统响应速度,并可有效抑制负载突变时对转速的影响,同时对转速和转子位置角的估计精度较高,使系统具有较强的鲁棒性。