基于感知实验的纹理触觉感知模型*
2022-01-18曹志勇
曹志勇, 吴 涓, 张 军, 何 聪, 陈 航
(东南大学 仪器科学与工程学院,江苏 南京 210096)
0 引 言
纹理触觉是人接触纹理表面时,所产生的触觉感觉。在纹理交互过程中,最终人手接受到的触觉刺激(如力),不仅与纹理表面自身的特征相关,还受按压力、扫描速度等人为因素影响。这些触觉刺激经过人的力触觉感知系统的响应和加工,最终产生如粗糙/光滑等触觉感受。触觉刺激以力、振动、皮肤形变等交互信息的形式存在,目前大多数研究从采集的纹理交互信息中提取特征参数,同时通过心理物理实验来度量人的主观纹理触觉感受,以研究触觉刺激与纹理触觉感受之间关系模型。该研究不仅对认识人自身极为重要,同时对虚拟力触觉再现、智能机器人、遥操作等领域也有指导性意义。
触觉感受的度量(metric)是心理物理学研究的范畴,也是纹理触觉特性研究的基础。目前多数研究采用估值法,该方法通常让受试者对限定形容词进行定量打分,由于受个体差异的影响大,存在数据差异大的问题。此外还有分类法,该方法让受试者根据材料相似性进行分类[1]。分类法的数据一致性较好,但是该方法假设同类之间无任何差异,这可能导致差异信息的损失。最后还有排序法,目前排序法被证明具有较好的稳定性和有效性[2]。
人与环境交互时的触觉刺激信息及特征参数可以通过不同的传感器采集。针对不同的触觉交互,力触觉刺激及其特征参数各有不同[3]。例如,Smith A M等人[3]利用三维力传感器测量了纹理交互过程中的接触力,并探究了力的变化率与感知粗糙度的关系。Natsume M等人[4]使用指套装置采集了纹理交互中的皮肤振动,并计算振动信号的能量,以探究振动刺激对纹理感知粗糙度的影响。以往研究中关注的交互信息比较单一,很少考虑客观刺激间交互作用对触觉感受的影响。
为了描述客观触觉刺激与主观感知度量之间的关系,很多研究者利用统计学模型,建立心理物理学实验参数之间的数学关系模型,较为典型的,如Shao Z等人[5]利用回归分析建立了交互特征与感知柔顺性的多层感知模型。此外还有使用神经网络等机器学习算法进行建模[6],该方法利于拟合非线性关系,但难以直观观察输入输出的关系。另外,还有专门针对人感知特性以及神经机制的建模方法[7],该方法要求对触觉神经机制了解比较深入。
本文针对如何确定主观感知特征参数以及客观刺激特征参数及两个问题,分别给出的解决方案是:针对主观触觉感受的度量问题,本文采用非度量多维尺度(non-metric multidimensional scales,NMDS)分析方法,从受试者的差异度排序实验中,确定主观感知特征参数的维度以及量化坐标。针对客观刺激特征参数的选取,本文从全面测量的力触觉交互信息(接触力/加速度/位移)中提取一组反映交互变化的特征参数,优选出与主观感知特征参数相关性高且互相之间依赖性小的作为客观刺激参数。最终,建立了优选的客观刺激特征参数与主观感知特征参数之间的回归分析模型。
1 实验与数据分析
1.1 纹理触觉感知实验原理
为了确定主观纹理感知特征的维度及量化坐标,本文采用NMDS分析方法。NMDS的目的是指将欧几里德坐标分配给一组对象,当给定对象之间的差异关系时,嵌入的坐标应尽可能紧密地遵守这些关系。
NMDS以多个不等式约束作为算法的输入,这些不等式约束可用一个三元组集合表示
S={(i,j,k)|Dij (1) 式中 三元组(i,j,k)为样本i与样本j之间的差异度Dij,小于样本j与样本k的之间差异度Djk。Wills J等人将NMDS求解过程总结为以下求解矩阵K的优化问题 (2) ∀(i,j,k)∈S,Kkk-Kii+2Kik-2Kjk≥1-ξijk (3) (4) 式中Kij为K的第i排第j列,tr(K)为K的迹;ξijk为引入的松弛变量,以允许不等式被违反;λ为一个可调节的正则化参数,可平衡不等式违反量和嵌入坐标维数之间的关系。 记矩阵X的列表示样本的嵌入坐标,由于存在关系K=XTX,因此最终求解出K,样本的嵌入坐标便可通过分解K得到。本文在MATLAB中,使用SeDuMi 1.02工具包对优化问题进行求解。 以往研究发现,纹理物体表面微观空间周期、高度和硬度是影响纹理触觉的主要物理参数[3,7,8]。为准确提供给受试者典型的纹理刺激,本研究采用和前人研究类似的规则栅格表面以及硬度可调的硅胶材料制作人工纹理样本,以模拟真实纹理的不同空间周期、高度和硬度属性。图1显示了矩形栅格纹理的结构原理图以及实物示意图。为了与前人研究具有可比性,每种纹理客观物理参数分别选取三个水平为:1)空间周期分别取5,9,16 mm;2)高度分别取1,2,4 mm;3)硅胶邵氏硬度分别选取9,24,41HC。根据三种水平的组合一共生成27种纹理样本,其在由纹理客观物理参数构建的三维坐标系中的分布如图2所示。 图1 矩形栅格纹理 图2 纹理样本在由客观物理参数构建的坐标系中的分布 开展心理物理实验的目的为了获得纹理样本间的主观差异度排序结果。这些主观数据将被作为NMDS算法的输入,以确定主观纹理感知特征的维度及量化坐标。具体实验过程为:在每一次试验中,参与者会被随机提供两个测试纹理样本和一个参考纹理样本。他们被要求判断哪个测试纹理在触觉感受上更接近参考样本。实际实验的操作过程如图3所示,为了防止视觉干扰,参与者透过遮布来抓握力反馈设备Geomagic Touch的探针,并在纹理表面均匀滑动来感受纹理。同时为了防止听觉影响,参与者戴上播放白噪声的耳机。在本文实验中使用的27类样本一共可以产生了2 925种不同三元组的组合。整个实验由30名受试者进行,每个受试者接受了90次比较试验,因此总共进行了2 700次比较。 图3 心理物理实验过程 通过对纹理差异度的排序实验,最终获得2 700次的主观差异度排序结果,记其中一次排序结果为三元组(i,j,k),其表示纹理i与j之间的差异度小于纹理j与k的之间差异度。最终排序结果以三元组集合的数据形式作为NMDS算法的输入(式(3)),继而算出纹理样本的嵌入坐标。 由于正则化参数λ是平衡不等式违反量和嵌入坐标维数的重要参数,本文进行了5次交叉验证以找到最佳的λ,结果显示,当λ=78时,嵌入的坐标具有最佳的泛化能力,且此时嵌入坐标维数为2。最终NMDS计算出的样本嵌入坐标在二维空间中的分布如图4所示。在图4中样本间距离大小可解释为纹理感知差异大小,因此该空间被称为纹理触觉感知空间。对比图2和图4可以发现,客观物理参数差异大的两个样本,在纹理触觉感知空间中差异也大。 图4 纹理样本在纹理触觉感知空间的分布 以往研究表明影响纹理触觉感知的交互信息主要包括力、加速度以及位移等信息。为此,本文利用三维力传感器采集纹理交互中的接触力,并利用加速度传感器采集振动信息,同时通过力反馈设备Geomagic Touch测量位移信息。三种信号均以1 kHz采样率进行同步采集。根据人的交互习惯,本文将交互信息的测量分为两个步骤:首先是竖直按压纹理的过程,具体是通过Geomagic Touch的探针对纹理施加最大2N力,并记录相应的位移(形变)。其次是在纹理表面水平滑动的过程,为了使实验条件统一,具体是利用Geomagic Touch的探针以平均100 mm/s的速度以及1N的法向接触力,在纹理表面上滑动来采集加速度、力等交互数据。 结合纹理触觉感知的前人研究,同时考虑纹理客观物理属性,本文在交互信息中提取了以下特征参数: 1)振动能量(E):振动能量常被用于衡量感知粗糙度的大小[4],其体现了频谱上的振幅大小。对于纹理i,计算振动能量的公式如下 (5) 式中ω为频率,PSD为滑动过程的法向加速度的功率谱密度。图5(b)显示了典型法向加速度的功率谱密度曲线,其中阴影部分区域表示振动能量。 图5 法向加速度 2)振动频率(f):振动频率(节奏)被认为是影响纹理差异的重要因素。因此对于纹理i,本文计算了滑动过程的法向加速度Azi的频谱峰值的频率 (6) 式中FFT(Azi)为滑动过程的法向加速度Azi的快速傅里叶变换。由于存在关系f=v/λ,当速度一定的情况下,振动频率f与空间周期λ成反比。可以看出振动频率反映了纹理空间周期的变化。 3)等效刚度系数(k):Piovari M等人[2]利用按压过程中力—位移曲线,研究了多种与硬度感知相关的模型,其中全局刚度系数被证明具有很好的效果。对于纹理i,等效刚度系数ki通过按压过程中的力—位移数据ci的线性回归来估计,计算公式如下 (7) 4)等效摩擦系数(u):先前的研究表明摩擦系数对感知纹理粘滞性具有显著影响。对此,本文对于纹理i,摩擦系数公式计算为 ui=Fx/Fz (8) 式中Fx为滑动过程的切向力,Fz为滑动过程的法向力。这两个力均通过5 Hz数字低通滤波器进行滤波,并取均值得到。 (9) 为了使得计算结果更加稳定,CRF通过加时间窗并取平均值方法计算。 通过相关分析确定客观刺激特征参数是否有效影响纹理感知空间分布。表1显示客观刺激特征参数与纹理嵌入坐标(P)之间的多元相关系数,以及特征参数之间的皮尔逊相关系数。从表中可以看出E,f,k,CRF与P的相关性都很高(相关系数均在0.8以上),而u与P相关性很弱。因此,本文选取E,f,k,CRF作为影响纹理触觉感受的主要特征参数,而u不做考虑。同时从表1中可以看出特征参数之间相关性都不高。但是E,k,CRF之间具有一定的相关性,说明越硬的纹理造成了更大的力/振动幅度上的变化。此外,f与CRF呈现一定的负相关,由于f反映了纹理空间周期的变化,说明空间周期对力的变化幅值具有一定影响,这与探针底部能否充分落入凹槽底部有关。 表1 客观刺激特征参数与纹理嵌入坐标之间相关系数矩阵 为了定量分析纹理客观触觉特征参数(振动能量E、振动频率f、等效刚度系数k、力的变化率CRF)与纹理嵌入坐标之间的关系,本文采用回归分析建立二者之间的模型。根据韦伯定理,主观感觉的强度与刺激强度的对数成正比,因此对客观触觉特征参数先进行对数转换。又考虑到这些特征参数之间的共线性,所以使用逐步方法来找到最佳模型。最终逐步回归分析结果如表2所示。 表2 逐步回归分析中客观刺激特征参数的标准系数与显著性水平 本文选择显著性水平P值小于0.05的特征参数表示纹理嵌入坐标,从表2可以看出,只有logCRF对维度2影响不显著。如果将纹理触觉感知空间的两个维度分别表示为dim1和dim2,并采用标准化的回归系数表示方程,则模型可以表示为 dim1=-0.241 logE-0.763 logf-0.207 logk+ 0.282 logCRF (10) dim2=0.460 logE-0.204 logf+0.568 logk (11) 标准回归系数大小体现了自变量对因变量的贡献大小,所以,从模型中看出f对维度1贡献度最大,而k对维度2的贡献度最大。从而说明本文通过感知实验确定的纹理感知空间两个维度,一个与空间周期相关性大,另一个与纹理硬度相关性大。在相似的纹理客观参数范围内,东南大学吴涓等人[8]研究了虚拟再现纹理的感知空间,结果显示二维纹理感知空间的两个维度可解释为空间周期和刚度系数,这与本文结论存在相似点。 最终式(10)回归拟合的R2为0.907(P<0.001),式(11)回归拟合的R2为0.951(P<0.001),说明自变量能很好地解释因变量,方程是有效的。因此当收集纹理交互中的力触觉数据,并提取E,f,k,CRF等特征参数,则可以通过建立的模型计算出纹理在主观感知空间中的坐标,继而计算纹理之间的感知差异。 本文通过建立回归分析定量研究客观刺激与纹理主观感觉之前的关系。在Natsume M等人[4]的研究中振动能量与感知粗糙度之间存在线性相关,且Smith A M等人[3]研究认为力的变化率与纹理感知粗糙度之间存在很高线性相关性,而本文通过回归分析也可以看出振动能量、力的变化率与纹理感知差异存在线性关系。 本文提出了从纹理触觉感知心理物理学实验中,利用NMDS分析方法确定主观纹理感知特征的维度及量化坐标,并建立主观感知特征参数与客观刺激特征参数(振动能量、振动频率、等效刚度系数、力的变化率)的回归分析模型,结果表明具有较好的相关性。本文模型对于虚拟力触觉再现、智能机器人、遥操作等领域均具有重要指导性意义。1.2 实验样本选取


1.3 实验步骤

1.4 基于NMDS的纹理触觉感知空间刻画

1.5 纹理触觉交互信息的采集与特征确定

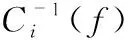

1.6 客观刺激特征参数的选取

2 纹理客观刺激特征参数与主观感知度量的关系模型

3 结 论
