高灵敏度蝶翼式微加速度计抗跌落性能分析与试验

单 恒， 侯占强, 肖定邦， 虢晓双， 曾承志， 吴学忠

(1.国防科技大学 智能科学学院，湖南 长沙 410073； 2.湖南天羿领航科技有限公司，湖南 长沙 410100；3.唐智科技湖南发展有限公司，湖南 长沙 410007)

0 引 言

微加速度计具有体积小、成本低、便于集成等突出优点，广泛应用于车辆、无人机、智能手持设备等军事和民用领域[1,2]。应用领域的不断拓展，特别是军事领域，不仅要求高精度，同时也对微加速度计抗冲击性能提出了更高的要求。

蝶翼式微加速度计是一种双差分扭摆式电容检测微加速度计[3]，采用全硅结构，通过干法刻蚀制备。双差分模式最大的优点是能够通过差分有效减小机械热噪声，减小制造误差影响，提高检测灵敏度。跌落冲击试验是检验微机电系统(micro-electro-mechanical system,MEMS)器件常用的方法，为更加清楚微加速度计敏感结构在跌落冲击中的受力问题。

本文通过静力和跌落冲击理论分析和试验，阐明跌落冲击对结构的破坏性影响，为高灵敏度蝶翼式加速度计抗冲击性能设计提供指导。

1 工作原理

蝶翼式微加速度计敏感结构如图1所示，该结构采用内置锚点，可等效为双端固支结构形式[3,4]。m1-m3和m3-m4组成两对质量块组，每组质量块均由钢性力臂与梁连接，且m1=m4>m2=m3，且梁到质量块的力臂均相等，设为Lm。设梁长为L，两对质量块组力臂到固定端的距离分别为L/4。

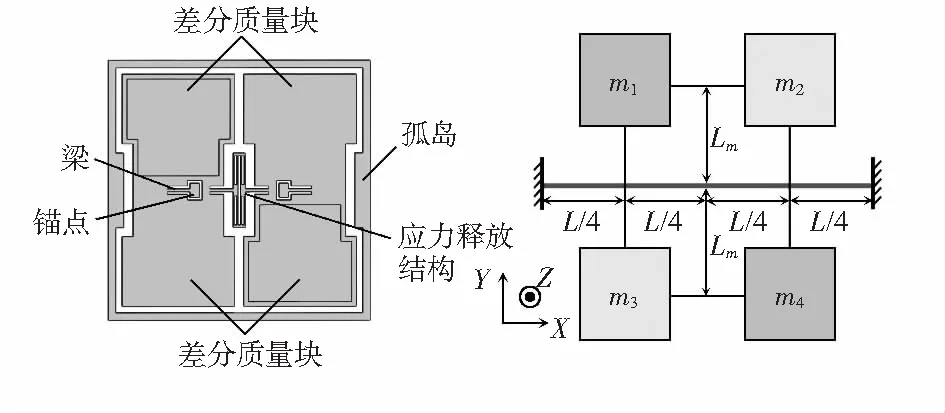
图1 蝶翼式敏感结构及简化模型

蝶翼式微加速度计敏感结构工作原理如图2所示，A和D为锚点，E1-E4为电容检测电极，分别与质量块m1-m4对应，组成四对电容。当有大小为a的加速度输入时，m1和m4向上运动，m2和m3向下运动，从而导致电容产生变化。

图2 蝶翼式结构工作模态

电容变化通过信号电路转换为输出电压，通过测量电压就可以得到输入加速度大小[5]。信号检测电路如图3所示。

图3 蝶翼式微加速度计检测电路

2 静力学仿真分析

蝶翼式微加速度计敏感结构X,Y,Z三个轴向受力时的运动及对应的模态频率如图4所示。

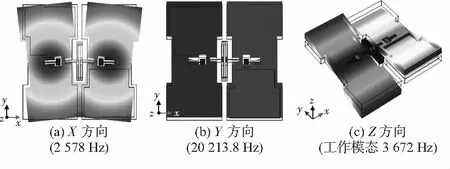
图4 XYZ三个轴向受力时的运动效果

采用COMSOL对蝶翼式微加速度计敏感结构的应力进行了仿真分析，静态1～10 000gn下的最大应力如图5所示。

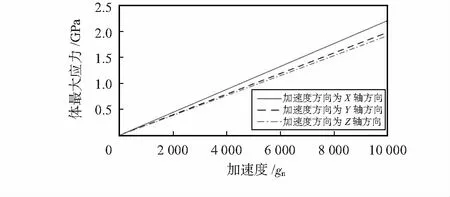
图5 优化前结构0～10 000 gn静态体最大应力

3 跌落受力分析

跌落时的受力为动载荷，一般情况下，以半正弦波来表示，其表达示为

(1)

式中θ值为π/t0；t0脉冲宽度(s)；a0为加度峰值(m/s2)。则XYZ三个轴向受力时的微分方程矩阵为

(2)

解式(2)，XYZ三个轴向可有统一形式的通解[6]。当初速度为v0，初位移为y0时，结构总位移(角度)为

(3)

式中B1和B2为

对于ASQ700跌落冲击试验机，加速度峰值、脉冲宽度、跌落高度及初速度如表1所示[7]。

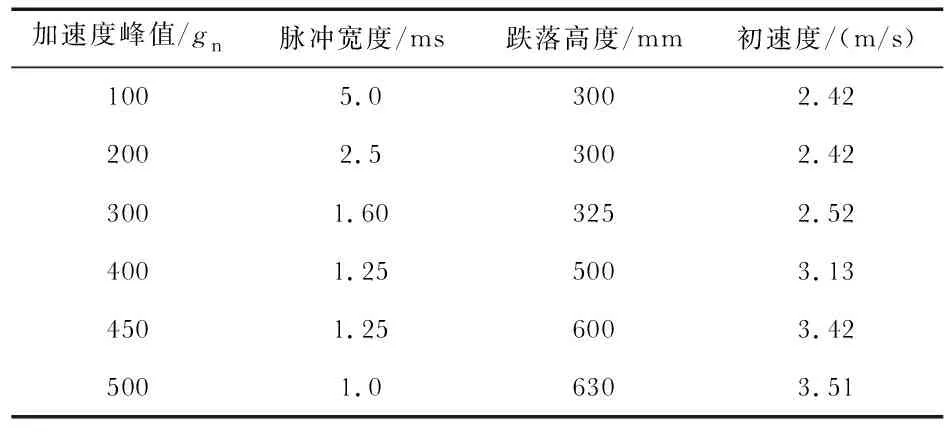
表1 跌落冲击相关参数

将结构三个轴向运动模态的频率、初始位移、初始速度及半正弦波频率和峰值代入式(3)中，计算出冲击时的最大位移ymax，再与同峰值加速度时静态位移yst相比，可计算出放大系数[8]，放大系数μ可表示为

μ=ymax/yst

(4)

放大系数与静态应力相乘可计算出冲击时的应力。结构在100～500gn冲击时放大系数和体最大应力如图6所示。

图6 跌落冲击时的放大系数和体最大应力

4 静力实验与跌落试验

4.1 静力试验

静力测试的目的是验证结构的断裂强度。测试用的样品如图7所示，通过在结构Z轴向施加一定的位移，观察结构的损坏情况。

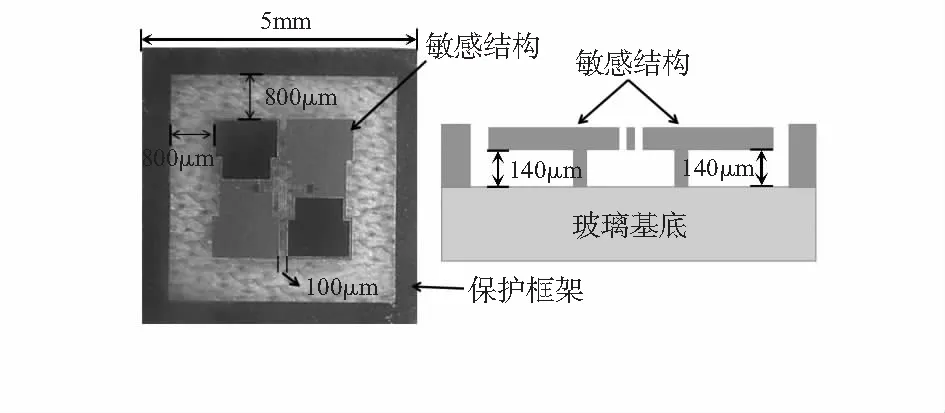
图7 敏感结构与外围框架尺寸关系

静力试验装置为FT—MTA02微力测试系统，如图8所示，测试时，将探针对准敏感结构质量块边缘。实际测试过程中，探针向下位移达到70 μm时，作用力达到系统极限。测试得到的位移与力之间的关系曲线如图9所示。

图8 FT—MTA02微力测试

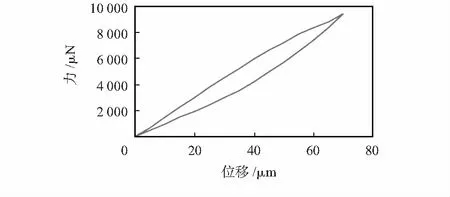
图9 微力测试位移与力的曲线图

利用COMSOL软件真质量块边缘位移为70 μm时结构应力，如图10所示，最大体应力为1.77 GPa，最大应力处在梁与锚点连接处。

图10 质量块边缘位移70 μm应力分布

由于设备具有受力保护功能，无法通过增加位移的方法使结构达到断裂极限，但通过试验证明该结构断裂极限大于1.77 GPa。

4.2 跌落试验

跌落实验使用ASQ700跌落冲击试验机，如图11所示，冲击试验台通过控制冲击台的高度和垫层厚度来控制加速度的峰值[7]。

图11 ASQ700跌落冲击试验机

为使一次冲击能够测验结构三个方向的冲击，将样品按照图11所示方式固定在顶端为立方体结构的螺丝上。然后将螺丝固定在样品安装台上。

根据跌落冲击理论分析，冲击试验初始值不能太大。本次试验从100gn开始冲击，直至结构损坏为止，每个量级冲击3次，每个方向选用3个样品。加速度峰值和脉宽设定及跌落高度以表1中的为参考。冲击试验结果如表2所示。

表2 跌落实验损坏情况统计表

结构的断裂点与静态仿真中的应力最大点一致，均在梁与锚点连接处，断裂效果如图12所示。断裂后的敏感结构质量块基本完整的掉落。

图12 结构损坏情况和梁在锚点处断裂效果

如图7所示，Z轴与基底之间仅有140 μm，两质量块之间距仅有100 μm。从表3中可知，Z轴向的冲击结构每次冲击都会碰撞到基底，X轴向的冲击结构两个质量块每次都会发生碰撞。对照图1中Y轴的应力曲线可知，Y轴在300gn冲击时应力为6.5 GPa，而Y轴在300gn冲击时全部损坏，可证明该结构梁的断裂极限约为6.5 GPa。X轴和Z轴在300gn冲击时并未达到6.5GPa，说明X轴和Z轴冲击时的结构损坏主要由碰撞所引起。

表3 X轴向和Z轴向跌落时敏感结构的碰撞速度

根据跌落受力分析，300gn跌落冲击时，Y轴应力最大为6.5 GPa，根据表2中试验结果可认为梁的断裂极限约为6.5 GPa，而X轴和Z轴在300gn冲击时并未达到6.5 GPa，说明X轴和Z轴冲击时的结构损坏主要由碰撞所引起。

5 结 论

本文通过对蝶翼式敏感结构静态仿真与跌落冲击受力进行理论分析，建立了跌落冲击数学模型，最后通过静力试验和跌落冲击实验证明了理论分析的正确性。通过理论计算与试验对比分析，证明跌落初速度是决定结构冲击应力大小的关键。依据断裂极限接近7 GPa[9]判断，Y轴向冲击下结构断裂由位移过大导致，X轴向和Z轴向冲击下结构断裂由碰撞导致。本文对研究微结构跌落冲击和如何提高微结构的抗冲击性能具有一定的指导意义。