共轴双旋翼无人机的建模与动力学仿真
2022-01-18吕宝亮史春景郝永平徐九龙刘成奇
吕宝亮,史春景,郝永平,徐九龙,刘成奇
(1.沈阳理工大学 机械工程学院,辽宁 沈阳 110000;2.北方华安工业集团有限公司,黑龙江 齐齐哈尔 161000)
0 引言
近些年以来,无人机在军事与民用上发挥了重要作用,展现出了广阔的应用前景,得到了大量的关注,被用于航拍、侦察、搜救等工作。与此同时,也出现了大量不同结构的无人机,主要包括多旋翼无人机、固定翼无人机和共轴式无人机。共轴双旋翼无人机由于结构比较简单、可以垂直起降、悬停、不需尾部螺旋桨,比较容易满足目前无人机小型化的要求,而逐渐在大量领域广泛使用[1]。参考现在已有的无人机结构,根据设计要求,本文设计了一款小型的共轴双旋翼无人机,对其进行了各零件的建模、装配和运动仿真以及实物测试,通过对旋翼转速的控制实现无人机上升、下降运动,并通过对舵机的控制带动桨盘实现周期变距,完成无人机的姿态控制。
1 共轴双旋翼无人机结构
共轴双旋翼无人机在结构上是两对旋翼上下分布,转速相同,转向相反,因此产生的反扭力矩可使无人机达到平衡,通过改变两电机的旋转速度,控制无人机的垂直升降运动。其中上桨盘是自平衡不可控的,只提供升力,下桨盘通过倾斜盘控制的周期变距来改变桨叶力矩的大小和方向,使桨叶的挥舞呈现周期性变化,完成无人机的横滚和俯仰运动[2]。
本文所涉及的共轴双旋翼无人机由上桨盘、下桨盘、电池仓、机身、操纵机构五部分组成,其结构如图1所示。

图1 共轴双旋翼无人机结构
2 共轴双旋翼无人机动力学建模
为了直观地描述无人机在飞行中的状态,选用大地坐标系OXYZ和机体坐标系oxyz来判断无人机当前姿态,设机体坐标系的原点与无人机质心相重合,x轴经过质心指向机头方向,即正方向;y轴经过质心垂直于x轴且与机体平行,定义无人机右侧为正;z轴经过质心且与共轴双旋翼无人机的空心轴线共线,向上为正,如图2所示。
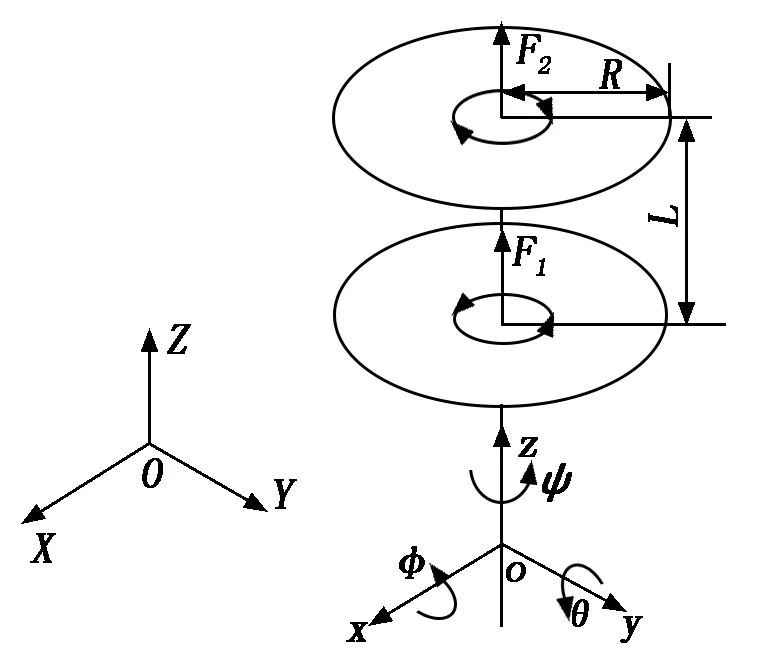
图2 飞行器坐标系以及简化模型
图2中,F1、F2分别为上、下旋翼的升力,Φ、θ、ψ分别为无人机的横滚角、俯仰角和偏航角,R为桨盘回转半径,L为上、下旋翼间距。
建立机体动力学方程时,在不影响研究结果的前提下提出3点假设[3]:①将飞行器看成刚体,且整体质量恒定;②忽略地球曲率,将地球表面作为平面;③将共轴双旋翼无人机质心与中心对称轴视为重合。
机体空间位置和机体速度之间的关系可通过机体坐标下的速度转化到大地坐标下的速度得到:
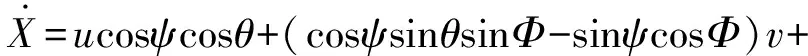
(cosψsinΦ+sinψsinΦ)w .


其中:u、v、w分别为机体质心速度在x、y、z轴的投影。
机体旋转角速度和姿态角之间有如下关系:
其中:p、r、q分别为机体旋转角速度在x、y、z轴上的投影,即横滚角速度、俯仰角速度、航向角速度。
由于空气的阻力,机身受到的水平方向阻力及诱导速度vi为:
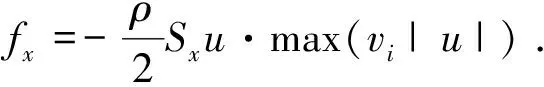
.
其中:ρ为空气密度;Sx、Sy分别为机身在x、y轴方向上的阻力面积;Tdw为下旋翼拉力。
机身在垂直方向受到的阻力为:
.
其中:Sz为机身在z轴方向上的阻力面积。
根据飞行动力学理论,上下旋翼所受到的推力为:
|Ti|=ρCTS(ΩR)2.
其中:CT为旋翼拉力系数;S为桨盘迎风面积;Ω为桨叶旋转角速度。
3 操纵机构性能分析
3.1 操纵机构受力分析
共轴双旋翼无人机在改变飞行状态时,操纵机构做周期变距过程中运动和受力较为复杂,其主要承受的载荷为铰链力矩。铰链力矩是指作用在旋翼上的载荷对旋翼变距轴线所构成的力矩,主要由桨叶的剖面气动力矩、桨叶的剖面气动阻尼力矩、离心力产生的力矩、周期变距产生的惯性力矩四部分构成[4]。
(1) 桨叶的剖面气动力矩为:
其中:R0为桨叶销轴孔到空心轴的距离;φ为方位角;c为阻力系数;Cm为旋翼的力矩系数;μ为旋翼的前进比;l为桨叶的无量纲径向位置。
(2) 桨叶的剖面气动阻尼力矩为:
其中:C1为旋翼剖面气动阻力系数。
(3) 离心力产生的力矩为:
M3=-IφΩ2γ.
其中:Iφ为桨叶剖面围绕所旋转轴线的转动惯量;γ为桨叶距角。
(4) 周期变距产生的惯性力矩为:

其中:I为桨叶剖面对旋转轴的转动惯量。
则总铰链力矩表示为:
M=M1+M2+M3+M4.
3.2 基于ADAMS的动力学仿真分析
为模拟操纵机构的力学性能,将无人机三维模型导入ADAMS软件,首先选取每个零件的材料,再对密度赋值,然后在上下旋翼与桨毂连接处、倾斜盘与拉杆铰链处添加转动副,空心轴与大地添加固定副,倾斜盘与鱼眼球副添加球副等约束;上、下旋翼转速均设置为3 000 r/min,通过添加step(time,0,0,1,5)+step(time,1,5,3,0)函数完成下桨盘在倾斜盘控制下的仿真过程。共轴双旋翼无人机的仿真模型如图3所示。

图3 共轴双旋翼无人机仿真模型
根据共轴双旋翼无人机的飞行状态,当其做俯仰横滚运动时,操纵机构做周期变距,即纵向周期变距和横向周期变距。在改变距角的状态下,分析倾斜盘在不同的倾斜角度时操纵机构的受力情况。
3.3 仿真结果
3.3.1 纵向周期变距
当倾斜盘倾斜5°时,由于上旋翼只能在Z轴方向为无人机提供升力,无其他角度变化,因此只观察下旋翼在各轴方向上单侧受力的变化情况。倾斜盘倾斜5°时单侧下旋翼升力变化如图4所示。
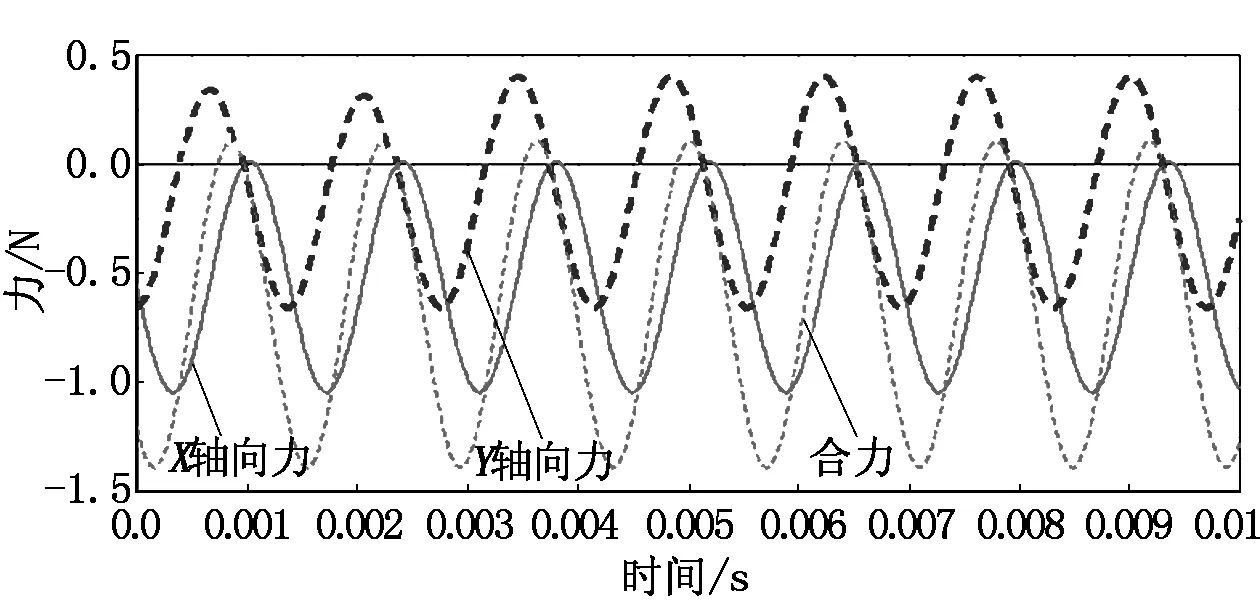
图4 倾斜盘倾斜5°时单侧下旋翼升力变化
由图4可看出:下旋翼单侧在Y轴方向上受力情况为正弦形式,围绕0 N上下波动;在X轴方向上受力情况为在0.0156 N~-1.043 1 N范围内波动;合力在0.108 N~-1.387 9 N范围内波动。考虑到另一侧升力变化情况,即在倾斜盘倾斜5°时,可使无人机在X轴方向上受到约2 N的分力。
倾斜盘倾斜7.5°时单侧下旋翼升力变化如图5所示。由图5可看出:下旋翼单侧在Y轴方向上的受力情况为正弦形式,围绕0 N上下波动;在X轴方向上的受力情况为在0.023 4 N~-1.564 1 N范围内波动;合力为在0.162 9 N~-2.079 2 N范围内波动。考虑到另一侧升力变化情况,当倾斜盘倾斜7.5°时无人机在X轴方向上受到约3 N的分力,与预测情况一致。
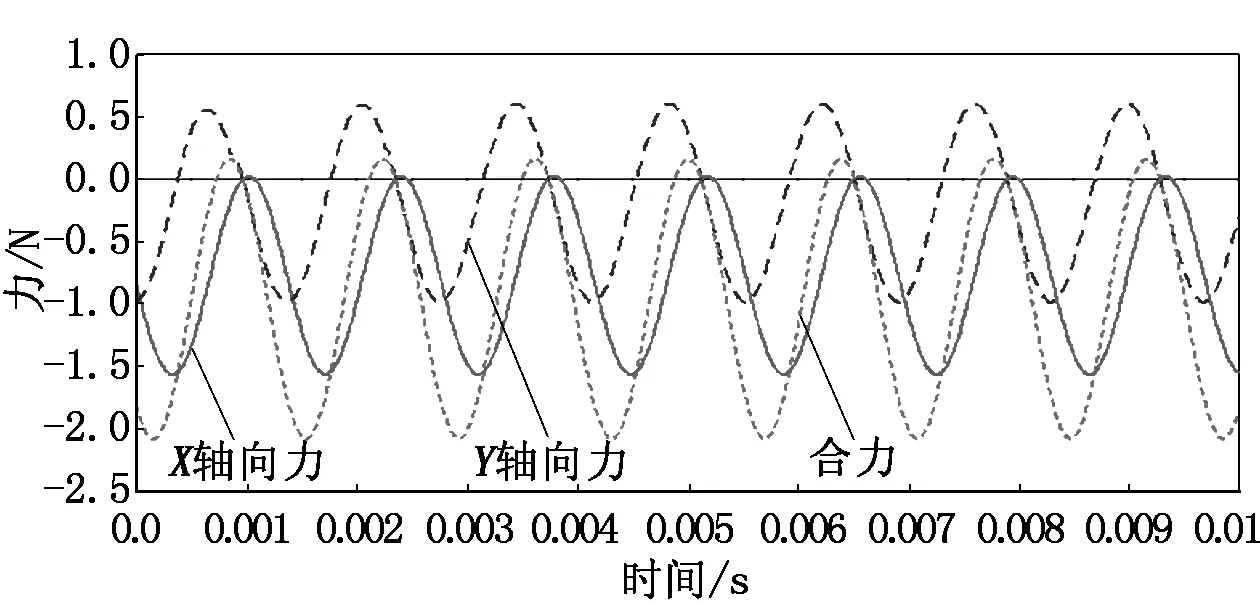
图5 倾斜盘倾斜7.5°时单侧下旋翼升力变化
倾斜盘倾斜10°时单侧下旋翼升力变化如图6所示。
由图6可看出:下旋翼单侧在Y轴方向上的受力情况为正弦形式,围绕0 N上下波动;在X轴方向上受力情况为在0.0312 N~-2.086 N范围内波动;合力在0.162 9 N~-2.079 2 N范围内波动。考虑到另一侧升力变化情况,当倾斜盘倾斜10°时无人机在X轴方向上受到约4 N的分力。

图6 倾斜盘倾斜10°时单侧下旋翼升力变化
3.3.2 横向周期变距
无人机做横滚运动时,舵机带动倾斜盘左右倾斜与俯仰运动相似,只有倾斜方向不同,方位相差90°,所以旋翼的各部件受力变化和载荷均与纵向周期变距时相同,故不进行过多阐述。
因此,共轴双旋翼倾斜盘在纵向或横向倾斜一定角度时:①X轴方向上的力使机体产生绕Y轴旋转的转矩将使其产生俯仰运动而改变其前飞速;②Y轴方向上的力使机体产生绕X轴旋转的转矩将使其产生侧向偏移及滚转运动。
4 结束语
本文以共轴双旋翼无人机为研究对象,介绍了共轴双旋翼无人机的结构和工作原理,建立了共轴双旋翼飞行器的三维模型和数学模型,并利用ADAMS进行了动力学仿真。通过仿真可知,倾斜盘伴随倾斜角度变大可以提供所需的升力变化,同时也可以满足载体改变飞行姿态所需的力。
