地震信号滤波器滤波性能研究

罗 浩 赵 驰

(1. 中国石油化工股份有限公司 石油物探技术研究院， 南京 211103； 2. 中国石化西北油田分公司 勘探开发研究院， 乌鲁木齐 830011)

地震波从激发、传播、接收到最终被地震仪记录下来，其中往往混有大量的干扰波[1]。通过滤波处理压制干扰波，可减轻其对最终成像剖面质量的影响[2-3]。对于地震信号中的相干干扰，主要采用切除、带通滤波、F-K域消除、小波变换分频去噪等方法进行去除[4]。本质上，带通滤波、F-K预测滤波、小波变换均采用的是切除方法[5-6]。由于有效信号同干扰信号在时域、频域上会相互交织，因此采用切除技术压制相干干扰时会对有效信号造成一定损伤[7]。此外，野外接收的地震信号中常混叠有大量的随机干扰，当其能量较大时，会严重影响动校正速度的分析以及静校正量的拾取，导致最终成像剖面质量不佳[8-12]。对于随机干扰的去除，目前有多种方法，如F-K滤波、径向预测滤波、多项式拟合法等[13-14]。以上方法主要是通过增强有效信号或抑制干扰信号的方法来提高地震信号的信噪比。此类方法在实际生产应用中取得了一定成效，但其应用需满足一定的信噪比，且有效信号相似。为此，我们根据实际地震信号的特点研究更加适用的滤波器，改善滤波性能，以提高地震信号的信噪比。

1 数字滤波器的设计

1.1 采用巴特沃思法设计IIR数字滤波器

采用巴特沃思法设计IIR(无限冲激响应)数字滤波器，其基本原理是：通过巴特沃思模拟滤波器得到模拟低通滤波器，再采用脉冲响应不变法获得IIR数字低通滤波器[15]。

以滤波器的脉冲响应为出发点，令数字滤波器的单位脉冲响应序列h(n)去模仿模拟滤波器的冲激响应ha(t)。即对ha(t)进行等间隔采样，使h(n)等于ha(t)的采样值，如式(1)所示：

h(n)=ha(nT)

(1)

式中T为采样周期。

令ha(t)的拉普拉斯变换为Ha(s)，h(n)的Z变换为H(z)，则由H(z)与Ha(s)的关系可得到式(2)：

(2)

由式(2)可知，脉冲响应不变法的实质是将模拟滤波器的s平面变换为数字滤波器的z平面，其标准变换关系为z=esT，如图1所示。

最后，由IIR数字低通滤波器通过频率变换获得具有其他相应特点的IIR数字滤波器。

1.2 采用等波纹法设计FIR数字滤波器

采用等波纹法设计FIR(有限冲激响应)数字滤波器，逼近误差函数[16-18]：

E(ω)=W(ω)[Hd(ejω)-H(ejω)]

(3)

式中：E(ω)为误差函数；Hd(ejω)为设计要求的振幅响应；W(ω)为正权重函数。

首先，在指定频带确定合适的W(ω)以控制峰值误差的大小；然后，采用Parks-McClellan算法调整幅度响应系数，使E(ω)的峰值绝对值为最小。

2 时域滤波的实现

2.1 滤波器的设计

(1) 采用巴特沃思法设计IIR数字滤波器。其主要技术指标有：通带上限截止频率(Fp)为0.03 kHz；阻带下限截止频率(Fs)为0.035 kHz；通带波纹(Ap)为1 dB；阻带衰减(As)为80 dB；采样率为0.25 kHz。图2所示为IIR数字低通滤波器振幅频率响应特性曲线。

从图2可以看出，采用巴特沃思法设计的IIR数字滤波器，其通频带内的频率曲线平坦而无起伏。这表明采用镶边法对理想滤波器进行镶边之后，吉卜斯(Gibbs)现象的消除效果较好。但在其过渡带上出现了斜坡，说明对频率的选择性变差。相比之下，滤波器阶数为500时振幅频率响应特性曲线的过渡带更陡、更窄，对频率的选择性更强。因此，采用巴特沃思法设计IIR数字滤波器时，在一定范围内滤波器的阶数越高其滤波性能越好。

(2) 采用等波纹法设计FIR数字滤波器。其主要技术指标有：通带上限截止频率(Fp)，为0.03 kHz；阻带下限截止频率(Fs)，为0.035 kHz；通带波纹(Ap)，为1 dB；阻带衰减(As)，为80 dB；采样率，为0.25 kHz。图3所示为FIR数字低通滤波器振幅频率响应特性曲线。

从图3可以看出，采用等波纹法设计的FIR数字滤波器，其通频带和阻频带均为等波纹，可以分别控制通频带和阻频带波纹的幅度。理想滤波器镶边之后，吉卜斯(Gibbs)现象的消除效果不太理想，通频带内的频率曲线仍出现不同程度的抖动(见图3a)。同时， 阶数为500时振幅频率响应特性曲线的通频带平坦而无起伏，吉卜斯(Gibbs)现象得到有效消除，且其阻频带的幅度很低，对不期望的信号作了有效压制。因此，采用等波纹法设计FIR数字滤波器时，在一定范围内增加滤波器的阶数可以有效地提升滤波器的滤波性能。

根据以上两种数字滤波器(IIR与FIR)的滤波性能分析，选用阶数为500的数字滤波器对理论地震信号与实际地震信号进行滤波试算，以验证新设计滤波器的滤波效果。由于篇幅所限，在此仅分析低通滤波器的效果。

2.2 理论地震信号测试效果分析

构建采样率为250 Hz的理论模型地震道：

x(t)=sin(2·pi·0.04t)+sin(2·pi·0.2t)+

sin(2·pi·0.4t)

对其进行以下滤波处理，以验证滤波器的准确性与稳定性。

(1) IIR数字低通滤波器滤波。理论信号经IIR低通滤波前后的对比情况如图4所示。从时域图与频域图的对比可以看出，经IIR数字低通滤波器进行滤波处理之后，理论地震信号中主频为10 Hz的低频成分得以保留，而主频为50 Hz的中频成分及主频为100 Hz的高频成分则被完全滤除。这说明本次设计的IIR数字低通滤波器完全达到了预期滤波效果。

(2) FIR数字低通滤波器滤波。理论信号经FIR低通滤波前后的对比情况如图5所示。时间域及频率域的对比显示，经FIR数字低通滤波器滤波处理之后，理论地震信号中主频为10 Hz的低频成分得以保留，而主频为50 Hz的中频成分与主频为100 Hz的高频成分则被滤除。这说明本次设计的FIR数字低通滤波器完全达到了预期滤波效果。

图4 理论信号经IIR数字低通滤波前后对比

2.3 实际地震信号时域滤波测试效果分析

使用本次设计的数字滤波器对野外采集的实际地震信号进行滤波处理，分析其滤波效果。

(1) IIR数字低通滤波器测试。分别对实际单道信号和单炮信号进行测试，效果如图6、图7所示。

采用本次设计的IIR数字低通滤波器进行滤波处理之后，单道及单炮实际地震信号中的低频地震信号被保留，而高频地震信号则被有效滤除，达到了预期效果。这说明所设计的IIR数字滤波器是稳定且可靠的。

(2) FIR数字低通滤波器测试。分别对实际单道信号和单炮信号进行测试，效果如图8、图9所示。

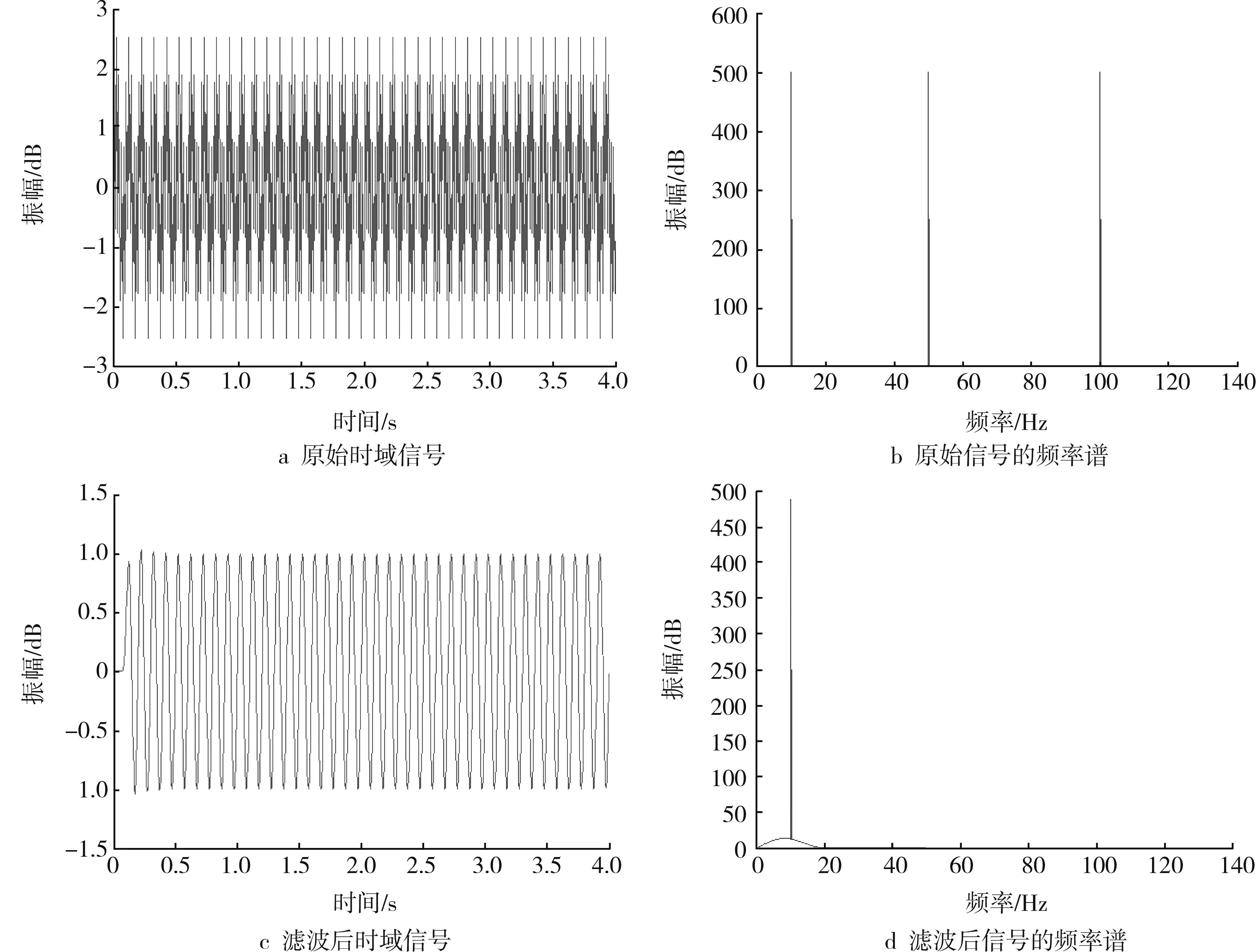
图5 理论信号经FIR低通滤波前后对比

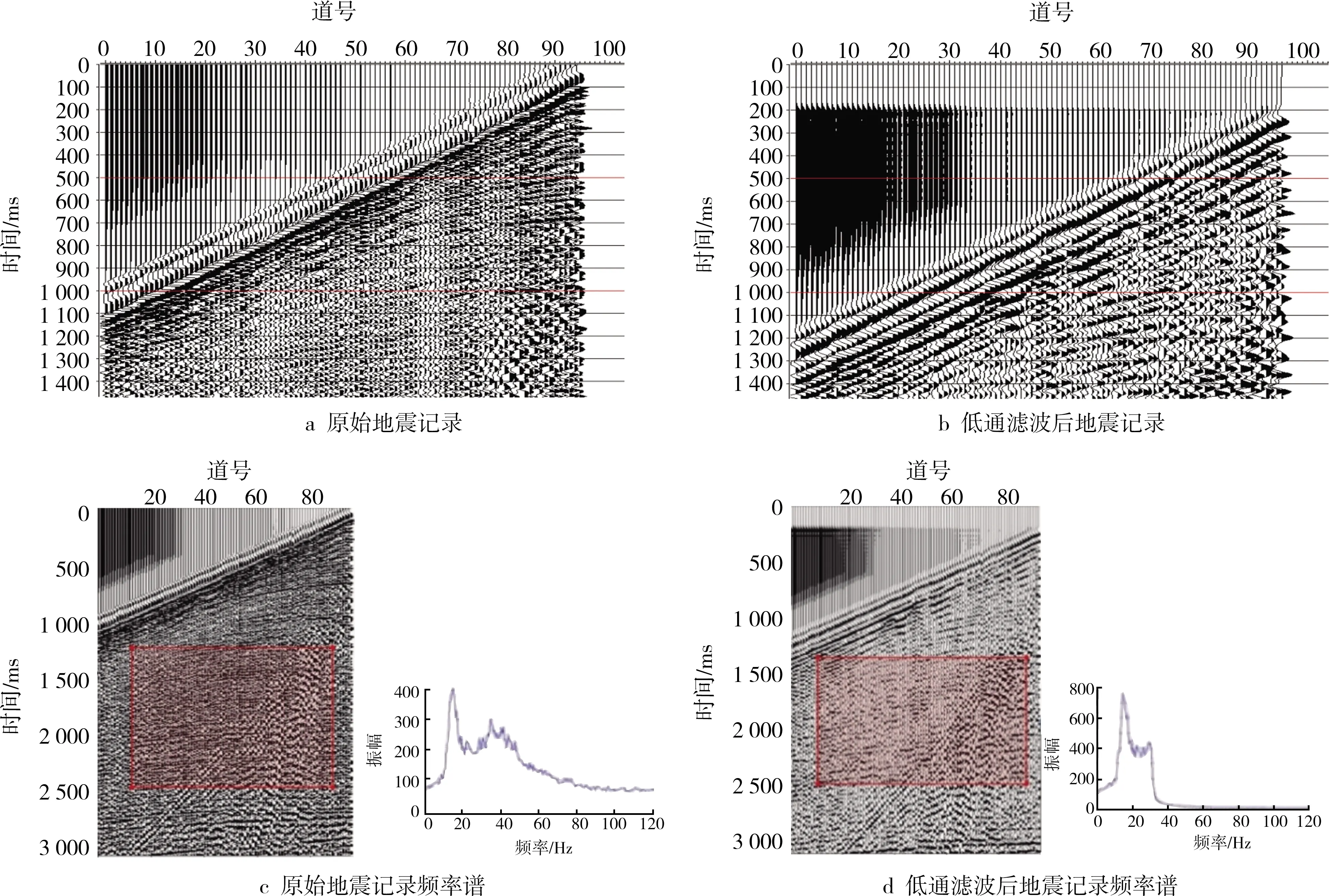
图7 单炮实际地震记录经IIR低通滤波前后对比

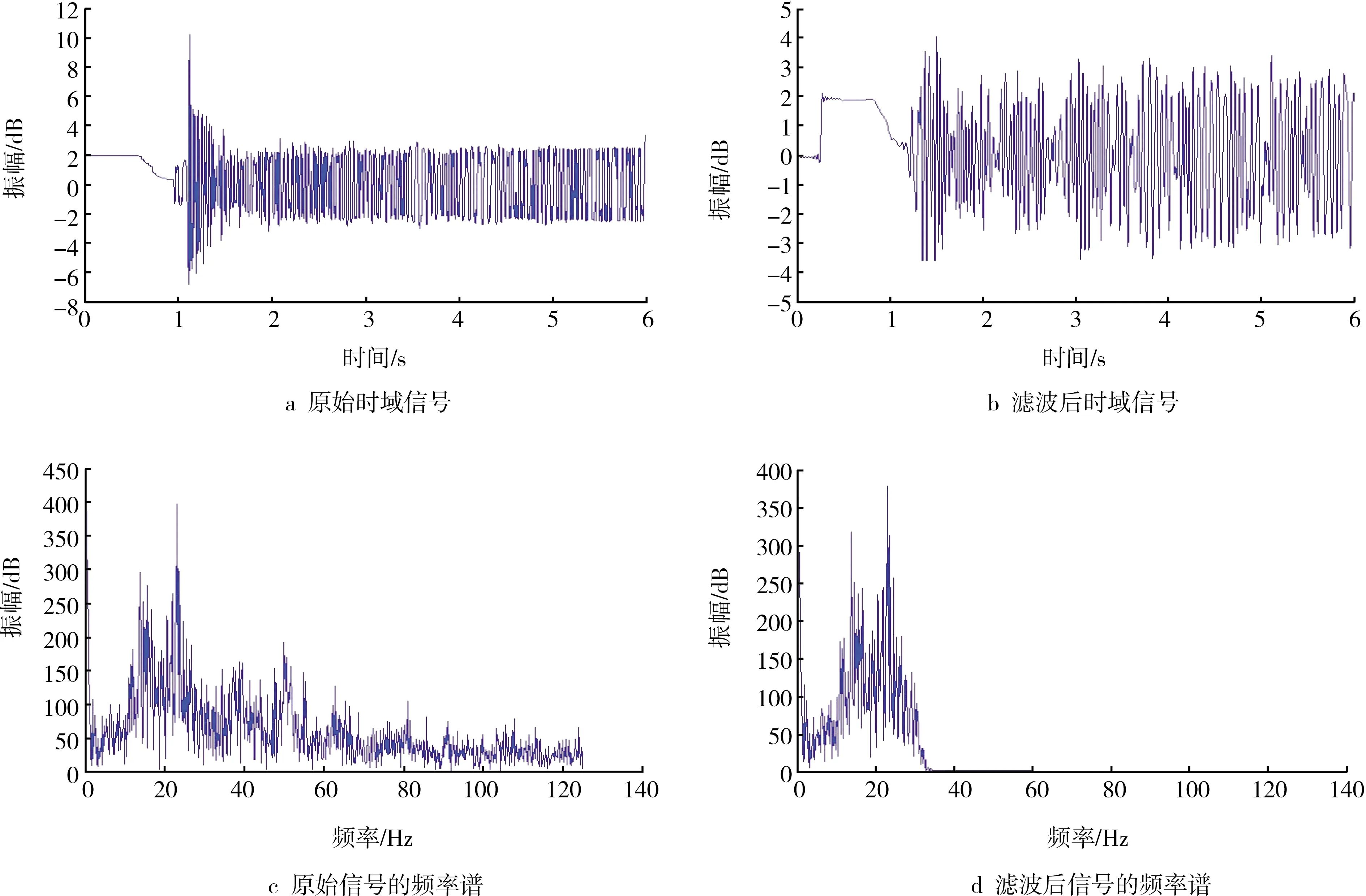
图8 单道实际地震信号经FIR低通滤波前后对比

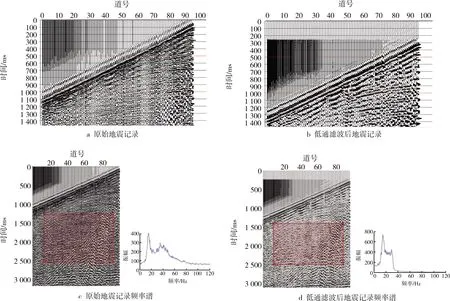
图9 单炮实际地震记录经FIR低通滤波前后对比

可以看出，经FIR数字低通滤波器滤波处理之后，单道与单炮实际地震信号中的低频信号被保留，而高频信号则被切除。说明本次设计的FIR数字低通滤波器的滤波效果良好。

3 结 语

本次研究采用巴特沃思法和等波纹法分别设计了IIR和FIR数字滤波器，用于地震信号滤波。测试结果显示，本次设计的滤波器性能可靠，滤波效果良好。研究中发现，采用巴特沃思法和等波纹法分别设计IIR与FIR数字滤波器时，在一定范围内增大滤波器的阶数，可以有效提高滤波器的滤波性能。采用巴特沃思法设计IIR数字滤波器时，利用镶边法对理想滤波器进行镶边，可以有效消除吉卜斯(Gibbs)现象，但其对频率的选择性变差。采用等波纹法设计FIR数字滤波器时，使用镶边法对理想滤波器进行镶边之后对吉卜斯(Gibbs)现象的消除效果不理想，其通频带内的频率曲线仍有不同程度的波动，在一定范围内增大滤波器的阶数可以进一步消除吉卜斯(Gibbs)现象。